不同弹性地基板的力学响应分析

不同弹性地基板的力学响应分析

郭晶晶

(同济大学道路与交通工程教育部重点实验室上海201804)

摘要以薄板理论为前提，通过汉克尔积分变换，推导在圆形均布荷载作用下k(文克勒)地基、E(半空间)地基，以及双参数地基3种不同弹性地基上无限大板的挠度和弯矩的解析解，得到在不同地基和荷载半径条件下荷载中心点的挠度系数、弯矩系数值，以及沿板半径方向的弯沉盆。分析3种地基模型及荷载半径对板力学响应量的影响差异。

关键词弹性地基薄板力学响应量

DOI10.3963/j.issn.1671-7570.2015.02.028

收稿日期：2014-11-24

水泥混凝土路面是最常用的2种路面类型之一。我国石灰石资源丰富，水泥产量居世界首位，为水泥混凝土路面的修建提供了有力的条件和发展空间。建立水泥混凝土路面结构在荷载和环境因素作用下力学响应的定量模型，是路面结构设计理论的基本依据[1]。

目前，世界各国刚性路面设计方法所依据的力学计算理论，主要是弹性地基板理论，具有代表性的弹性地基模式，是以地基反应模量表征的温克勒地基、考虑剪切的双参数地基以及以弹性模量和泊松比表征的弹性半空间地基。相对于解析解的计算研究，国内外利用限差分法、有限条法、有限元法和边界元法等数值解法解决弹性地基板的问题更为普遍[3-5]，3种弹性地基模型对板的影响也尚无系统的分析。文献[6]中已给出k地基与E地基上薄板的解析解，本文利用汉克尔变换推导双参数地基上薄板的解析解，分析3种地基模型及荷载对板力学响应量的影响差异。

1不同地基模型

k地基是Winkler于1867年在计算铁路路轨时提出的一个假设，他认为土介质表面任一点处的位移w与作用在该点的应力p成正比，即p(r)=k0w(r)与作用在其他点的应力无关。

弹性半空间地基模型是把地基假设为均匀、各向同性、弹性的半无限体。与k地基模型相比，这种模型属于连续介质模型，不仅可以反映荷载作用范围内土体的沉降变形，也能反映荷载作用范围外土体的位移。

k地基理论虽然简单直观，但不能很好地描述土体的连续性；而弹性半空间连续介质模型高估了地基的扩散能力，在数学上较为复杂，难以在实际工作中得到广泛应用。为此，人们提出了介于它们之间的一类地基模型，即双参数地基模型。双参数地基的力学实质就是在互不相关的线性弹簧上铺一恒定水平张力的薄膜，即

2薄板假设

小挠度薄板，指这种板在荷载作用下的挠度w与板厚h相比是一个微小量(w≪h)。分析小挠度薄板结构弯曲问题时，采用如下3个基本假设。

(1) 竖向的正应变εz可忽略。

(2) 竖向压应力、剪应力的变形可忽略。

(3) 中性面无拉伸与压缩变形。

3双参数地基板的微分方程

(1)

式中：k0为地基反应模量；k2为表征地基横向联系的弹簧系数；q(r)为均布荷载。

利用汉克尔积分变换

(2)

引入板相对弯曲刚度半径l，得到板挠度表达式

(3)

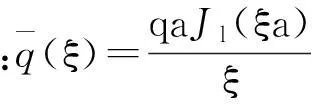
将板的挠度表达式带入弯矩表达式中，推得

(4)

圆形均布荷载作用下的弹性地基上无限长大板，其板挠度w，截面法向弯矩Mr、切向弯矩Mθ可用挠度系数φw，径向弯矩系数φMr,切向弯矩系数φMθ表征。其中：径向弯矩系数φMr、切向弯矩系数φMθ也可用2个弯矩参数AM，BM表征，即：

式中：P为圆形均布荷载总量,P=q0πa2。

不同地基、板模型和荷载类型条件下的无限大板的挠度系数φw，弯矩参数AM，BM的汉克尔变换解可统一表示为

其中，不同地基的F(t)也不相同，见表1。

表1　均布荷载作用下的函数 F( t)和系数 C w

4不同地基模型的比较分析

当E=30 000MPa，k0=100 MPa/m时，分析不同地基假设和荷载半径对挠度系数φw及弯矩参数AM，BM的影响。

在圆形均布荷载作用下，2种地基(k地基、E地基)薄板的挠度系数φw、弯矩参数AM，BM与距中心的相对距离ρ的关系曲线见图1。由图1a)可见，2种地基的挠度系数φw与距中心的相对距离ρ的关系曲线形状相似，但k地基的φw值明显小于E地基的φw值，且收敛也较快，在ρ=4附近越过零位；其次，荷载圆相对半径α对挠度系数φw的影响仅局限于ρ<1.5。从图1b)，c)可见，在荷载圆相对半径α较小时，2种地基的弯矩参数AM，BM很相近，随着荷载圆相对半径α的增大，两者的差异稍有增加，另外，在ρ∈[0.5,2.5]范围内AM的差异较明显。

荷载圆中心点2种地基的挠度系数φw0，弯矩参数AM0与荷载圆相对半径α的变化规律见图2。

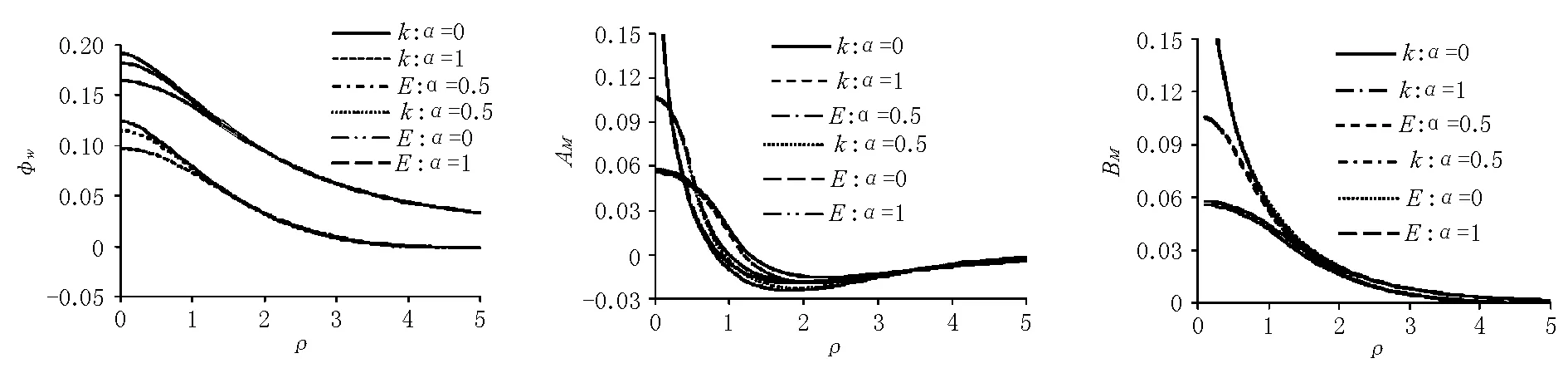
a)φw-ρb)AM-ρc)BM-ρ

图12种地基薄板的φw，AM，BM图

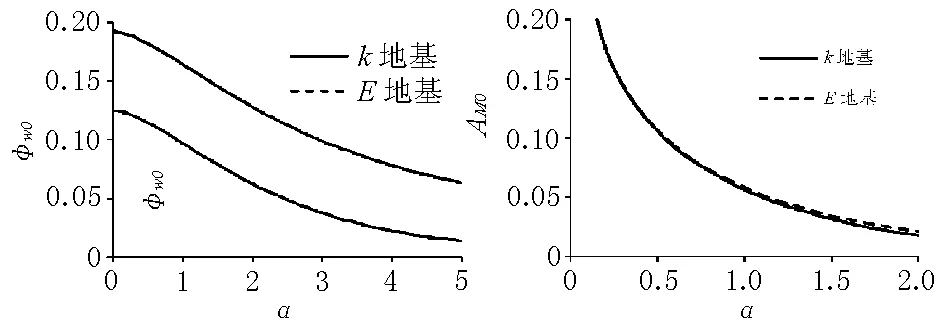
a)φw0-αb)AM0-α

图22种地基薄板荷载中心点的φw0，AM0图

由图2可见，2种地基的荷载圆中心点的挠度系数φw0-α曲线基本平行，E地基的φw0值较k地基的φw0值大0.067 5；在α较小时，2种地基的荷载圆中心点弯矩参数AM0十分相近，但E地基的AM0随α增大而衰减的速度较小，当α<0.5时，两者相差小于0.7%，当α=1时，E地基的AM0值较E地基的AM0值大3.8%，当α=2时，E地基的AM0值较E地基的AM0值大20%。

均布圆形荷载(α=0.2)作用下的双参数地基上薄板，地基横向联系参数θ对薄板的挠度系数φw的影响规律见图3。

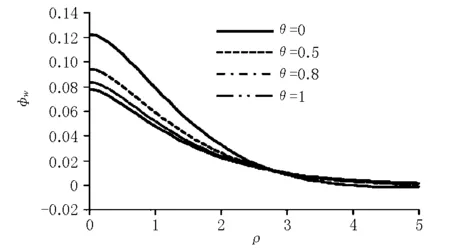
图3　双参数地基薄板的φ w-ρ图

由图3可见，随着地基横向联系参数θ的增大，荷载及附近区域板挠度变化幅度增大，在ρ≥2.8区域板挠度变化稍有减小；双参数地基板的最大挠度系数φw0、最大弯矩参数AM0均减小，减少的幅度附着荷载圆相对半径α的加大而略有减小，见图4。

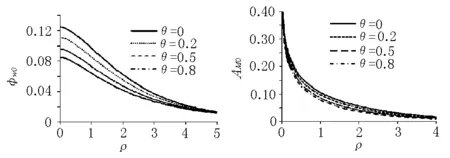
a)φw0-αb)AM0 -α

图4双参数地基薄板荷载中心点的φw0，AM0图

4结论

(1)k地基的挠度系数值明显小于E地基，但是挠度变化率基本一致且快速收敛。

(2) 随着荷载半径的增大，弯矩系数AM，BM差异越来越大，但随后又各自迅速收敛。

(3) 双参数地基是介于k地基与E地基之间的一种地基模型，横向联系系数θ对挠度的影响比对弯矩的影响更加显著。

参考文献

[1]姚祖康.水泥混凝土路面设计理论和方法[M].北京:人民交通出版社，2003．

[2]吕惠卿，张湘伟，成思源．水泥混凝土路面力学性能研究综述[J].重庆大学学报:自然科学版，2005，28(6)：60-63．

[3]熊渊博，龙述尧．用无网格局部Petrov-Galerkin方法分析Winkler弹性地基板[J].湖南大学学报:自然科学版，2004，31(4)：101-105．

[4]李宁.Winkler地基上弹性薄板求解的有限差分法[J].解放军理工大学学报:自然科学版，2004(5)：64-66．

[5]MELERSKI E S．Simple computer analysis of circular rafts under various axsymmetric loading and elastic foundation conditions．Proceedings of Institute of Civil Engineers，Part 2：Research and Theory，1990，89：407-431．

[6]朱照宏，王秉刚，郭大智.路面力学计算[M].北京：人民交通出版社，1985．

Mechanical Response Analysis of Different Elastic Foundation Plate

GuoJingjing

(Key Laboratory of Road and Traffic Engineering if Ministry of Education Tongji University, Shanghai 201804, China)

Abstract：On the premise of thin plate theory, three different deflection and bending moment analytical solutions of Winkler foundation, E (half space) foundation and double parameters foundation are deduced through the Hankel integral transformation. And the center deflection, bending moment coefficient and deflection basin along the radius direction of the elastic foundation plate on the condition of different foundation and the load radius are got. The difference and effect of the three kinds of foundation model and the load radius on the mechanical response are analyzed.

Key words: elastic foundation plate; thin plate; mechanical response