钢箱-混凝土组合拱桥受载全过程分析

钢箱-混凝土组合拱桥受载全过程分析

周远智朱金波邓晓红

(贵州省交通规划勘察设计研究院股份有限公司贵阳550081)

摘要了解钢箱-混凝土组合拱桥受载全过程的力学行为，采用有限元程序ABAQUS建立重庆江津笋溪河大桥的全桥模型，分析了在承载能力极限状态下全桥的力学行为。分析结果表明，在承载能力极限状态下，结构的破坏表现为塑性破坏，跨中正弯矩布载时的超载能力为12.2倍汽车荷载，拱脚负弯矩布载时的超载能力为16倍汽车荷载。

关键词拱桥ABAQUS力学行为

DOI10.3963/j.issn.1671-7570.2015.02.024

收稿日期：2015-03-09

在我国西南地区，山高谷深，地形条件极其复杂，随着高速公路的快速发展，在此类地区修建拱桥能充分发挥其优势。然而常规拱桥施工周期长、结构整体性能差、施工费用高等缺点限制了拱桥的应用，钢箱-混凝土组合拱桥[1-2]的出现成功克服了常规拱桥的缺点，其特有的结构形式和施工方法开拓了拱桥的应用前景。钢箱-混凝土组合拱桥作为一种新型的桥梁结构形式，为了全面理解其受载全过程的力学性能，了解其结构破坏的过程和形态，把握结构在给定荷载下的安全储备或超载能力，有必要对其进行受载全过程分析研究。

1钢箱-混凝土组合拱桥构造

钢箱-混凝土组合拱桥根据主拱各个位置的不同受力情况，合理组合钢材和混凝土，充分发挥2种材料的优势，由此将主拱拱肋分为4个区段，分别为拱脚区段、次拱脚区段、过渡区段以及跨中区段。

2有限元模型

针对复杂的全桥结构，采用试验研究其受载全过程的力学行为受到试验方法、试验场地的限制以至于很难实现，因此本文利用ABAQUS有限元程序对主拱进行受载全过程模拟分析。钢箱、横隔板等钢材部件采用三维壳单元(S4R)模拟，混凝土采用实体单元(C3D8R)模拟。根据文献[3]，混凝土与钢箱之间的接触全部采用了程序提供的“绑定约束(TIE)”模拟，在拱脚处采用了固定约束边界条件。全桥有限元模型见图1。

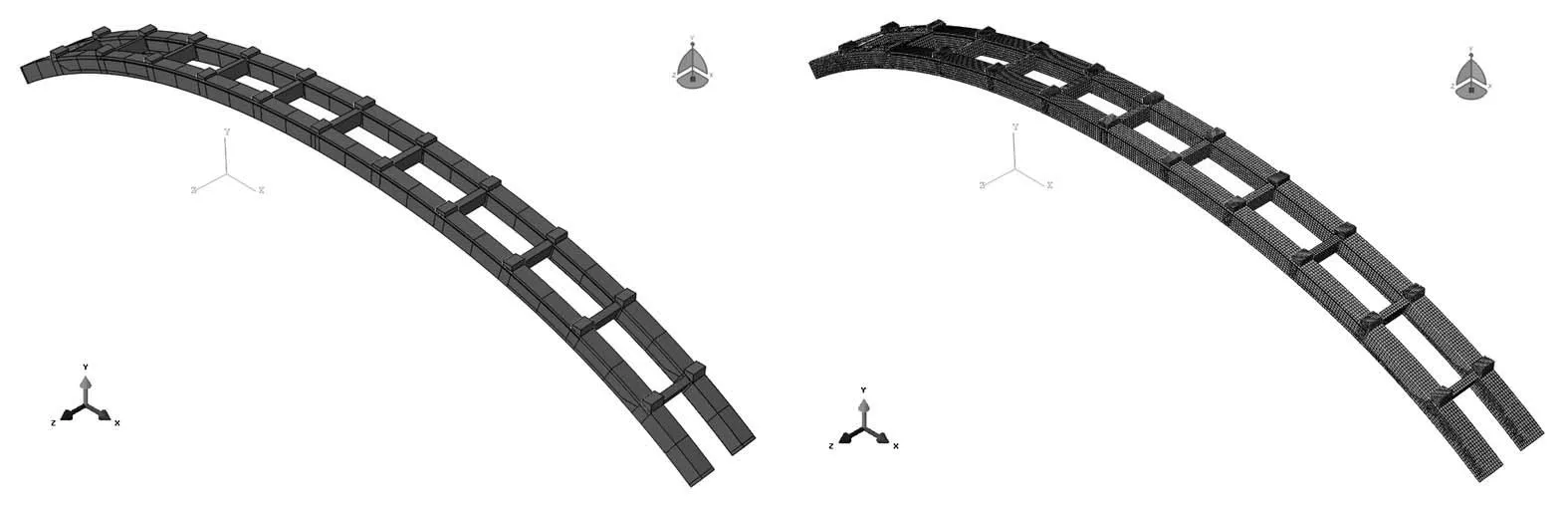
a)主拱几何模型b)主拱有限元模型

图1主拱有限元模型

3钢箱-混凝土组合拱的极限承载能力研究

本文在跨中正弯矩布载时加载大小为恒载+13活载，拱脚负弯矩布载时的加载大小为恒载+19活载，其中恒载大小为9 061.6kN，跨中最不利布载时活载大小为695.2kN，拱脚最不利布载时活载大小为827.7kN。

3.1　跨中正弯矩布载

(1) 在P=0.77Pu时(其中Pu=18 099.2 kN)，主拱钢箱在1/4截面应力达到345 MPa，受压屈服，此处没有底板混凝土的约束。

(2) 当荷载增加至P=0.87 Pu时，跨中截面钢箱顶面应力达到345 MPa，受压屈服。另外，由于1/4截面处底板钢箱较为薄弱，此时钢箱的屈服点已经由底板发展至腹板，其顶板混凝土应变超过其极限拉应变，部分被拉裂。

(3) 当荷载增加至P=0.97 Pu时，1/4截面处屈服点继续往腹板高度方向上升，顶板混凝土的拉应变急剧增加，全部被拉裂，跨中钢箱顶板受压屈服、底板受拉屈服，跨中顶板混凝土被压碎。此时，跨中截面位置处形成塑性铰，主拱达到其极限承载能力。

其中0.77,0.87,0.97 Pu对应的活载大小的倍数分别为7,9.6,12.2。

在各特征荷载作用下的主拱应力云图见图2。

a)P=0.77 Pub)P=0.87 Puc)P=0.97 Pu

图2跨中正弯矩布载主拱应力云图

跨中截面的荷载-位移曲线见图3，荷载比例系数为1时表示加载到13倍活载。当荷载达到7倍活载(荷载比例系数为0.54)之前，荷载位移曲线基本呈直线，主拱处于弹性阶段，当荷载达到7倍活载时，1/4截面钢箱底板受压屈服；当荷载增加到9.6倍活载(荷载比例系数为0.74)时，跨中截面钢箱顶板受压屈服，顶板混凝土尚未被压碎，此时1/4截面的钢箱底板屈服点向腹板上移；当荷载增加到12.2倍活载(荷载比例系数为0.94)时，跨中截面钢箱顶板屈服点向腹板下移，钢箱底板也受拉屈服，顶板混凝土达到其极限压应变，混凝土被压碎，此时1/4截面位置附近钢箱屈服面积更大，主拱达到其极限承载能力。

图3　跨中截面荷载-位移曲线

3.2　拱脚负弯矩布载

(1) 当P=0.59 Pu时(其中Pu=24 786.9

kN)，在加载侧拱脚截面位置，主拱钢箱上缘应力达到345MPa，受拉屈服，此时非加载侧拱脚1/4截面顶板混凝土部分拉裂。

(2) 当荷载增加至P=0.71 Pu时，非加载侧拱脚1/4截面钢箱底面应力达到345 MPa，受压屈服，顶板混凝土开裂加剧。

(3) 当荷载增加至P=0.87 Pu时，加载侧拱脚钢箱底板受压屈服，该侧1/4截面钢箱顶面受压屈服、底面受拉屈服，在该侧次拱脚区段结束位置附近钢箱顶面受压屈服；另一侧拱脚处钢箱底面受拉屈服，在该侧满填区段结束位置处钢箱顶面受压屈服。在非加载侧1/4截面的钢箱屈服面积进一步增大，该侧 1/4截面顶板混凝土全部开裂。

(4) 当荷载增加至P=0.9 Pu时，加载侧拱脚1/4截面以及非加载侧拱脚1/4截面的钢箱屈服面积进一步增大，加载侧1/4截面顶板混凝土达到极限压应变而被压碎，且此时的主拱由于钢箱的屈服形成了塑性铰，达到了其极限承载能力。

其中0.59，0.71，0.87，0.9 Pu对应的活载大小的倍数分别为6.7，10.3，15.1，16。

在各特征荷载作用下的主拱应力云图见图4。

a)P=0.59 Pub)P=0.71 Puc)P=0.87 Pud)P=0.9 Pu

图4拱脚负弯矩布载主拱应力云图

跨中截面的荷载-位移曲线见图5，荷载比例系数为1时表示加载到19倍活载，当荷载达到6.7倍活载(荷载比例系数为0.353)之前，荷载位移曲线基本呈直线，主拱处于弹性阶段，当荷载达到6.7倍活载时，加载侧拱脚截面钢箱顶板受拉屈服；当荷载增加到10.3倍活载(荷载比例系数为0.542)时，非加载侧1/4截面底板受压屈服；当荷载增加到15.1倍活载(荷载比例系数为0.795)时，加载侧1/4截面钢箱顶板受压屈服、底板受拉屈服；当荷载增加到16倍活载(荷载比例系数为0.84)时，主拱达到其极限承载能力。

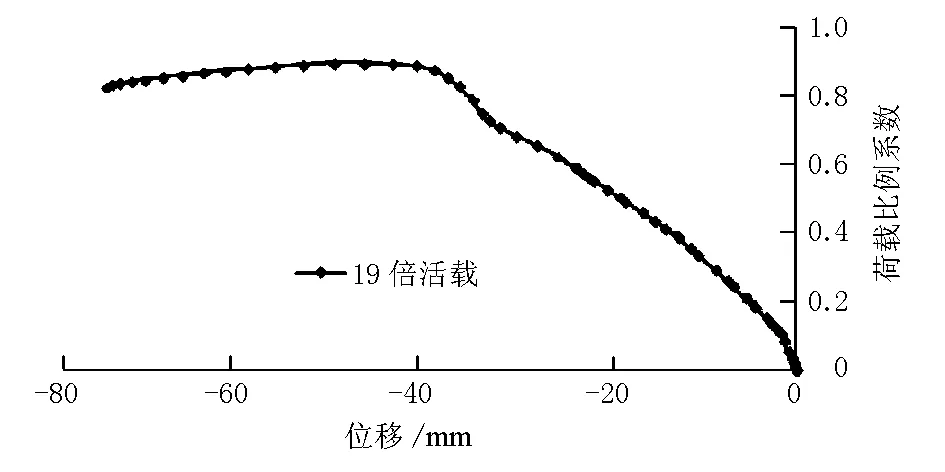
图5跨中截面荷载-位移曲线

4结论

(1) 在沿主拱顶面的应力分布中，次拱脚区段顶板钢箱的应力突变比较明显。可见，混凝土对钢箱力学性能影响十分显著，因此，在钢箱-混凝土组合结构设计中对于受力敏感区段应合理组合钢材和混凝土。

(2) 跨中正弯矩和拱脚负弯矩布载下主拱的破坏形式均为钢箱屈服，最后混凝土被压碎，形成三铰拱，表现出明显的塑性破坏形态。

(3) 对比跨中截面最不利布载下和拱脚截面最不利布载下的主拱极限承载能力可知，笋溪河大桥在跨中截面最不利布载下先于拱脚最不利布载而发生破坏，其极限承载能力为0.97 Pu，其中Pu=18 099.2 kN。

参考文献

[1]聂建国.钢-混凝土组合结构桥梁[M].北京:人民交通出版社,2011.

[2]林宗凡.钢-混凝土组合结构[M].上海:同济大学出版社,2004.

[3]范亮.钢箱-混凝土组合拱截面受力行为与设计原理研究[D].成都：西南交通大学,2010.