“带着问题来，带着问题走”的探究式课堂教学模式

吴延红 程秀丽 王改霞

摘 要：主要针对当前大多数应用型本科院校课堂模式存在的不足，研究出一种能很好地培养学生创新能力的新型教学模式—带着问题意识的探究式课堂教学模式，旨在提高学生学习的积极性，很好地参与到《高等数学》的课堂教学中，同时培养学生的创新能力。

关键词：课堂教学模式；创新能力；学习兴趣

中图分类号：G4

文献标识码：A

文章编号：16723198（2015）23022402

1 培养学生的问题意识

中国传统的教学模式主要重视教师的教，而对于学生是否可以能动的学习关注度较低。大部分学生在每堂课结束时只是学到了老师在课堂上所讲的知识，但他们对所学知识一般都没有太多疑问和问题，所以思考和创新的空间非常小。虽然近几年国家一直提倡素质教育，但受到长期传统教学模式的影响，素质教育实施的过程并不是一帆风顺。

要想让学生真正融入并参与到课堂教学中来，教师可以在课堂上逐渐培养学生的问题意识。当讲到一个知识点时，教师可以在多个角度和层面对该知识点进行延伸，启发学生从不同的角度对该知识点提出不同的问题，同时让学生在教师的指导下通过小组讨论等方式自己解决问题，通过不断解决问题培养学生学习的兴趣及参与课堂的积极性。

2 将“教学内容”问题化

为了能让《高等数学》这门课变成学生喜欢的一门课，使其有用性真正得以体现，我认为授课教师应该做到以下几点。

（1）将每堂课的教学内容进行整合，在讲解每个知识点时，合理创设一些问题情境。

对于《高等数学》函数的极值，最值及其应用这堂课，教师可以根据所教的专业创设不同的问题情境。

（2）启发学生将教学内容转化为多个相互联系的小问题。

为了让学生能够顺利解决提出的问题，可以根据情况将学生分成小组，让每个小组通过自学和集体讨论的形式将教学内容转化为相互联系的小问题，通过解决每个小问题进而让学生独立解决情境问题。对于所讲的每个案例，首先根据已知题目，引导学生分析这是一个什么问题；其次分析利用什么数学知识来解决这个问题；再次分析如何利用相应知识来解决这个问题。

（3）引导学生在解决问题的同时提出新的问题。

首先，教师在给学生讲解知识的同时，鼓励学生提出与知识点相关的各种问题，然后通过对问题的解决达到对知识点的掌握；其次，在每解决完一个知识点的问题后，教师应该引导学生提出跟此知识点紧密联系的下一个问题，根据合理性对学生的问题给出评价，然后进入下一个知识点的学习。

3 利用“问题”激发学生的学习兴趣

对于《高等数学》这门大部分学生望而生畏的课程而言，如何将学生从酣睡，手机游戏，聊天等非正常状态中解救出来，进而如何激发他们对这些枯燥而抽象的知识的兴趣，是每一位教师需要深思的问题。

我认为，利用各种与知识点相关的问题来引起学生的注意力是非常有效的。我们在授课过程中可以根据教学内容的不同设计不同的问题，这些问题可以是贴近现实生活的，最好是来源于生活的，可以是跟学生所学专业相关的，也可以是与本知识点相关的前沿研究问题。通过问题的设置给学生布置相应的解决问题的任务，让学生通过讨论给出解决问题的方法。

比如我们在讲解“函数的极值，最值及其应用”这堂课时，如果单纯地去讲其概念及其求法，学生肯定没有什么兴趣，教师可以在备课时将每个知识点设计成多个相互联系的小问题，在讲函数的极值的概念时，教师可以设计各省市楼房的高度，各班级学生的身高等问题帮助学生理解概念，最值的应用教师可以设计多个不同的案例，引导学生用自己的方法找出解决方案。

4 在解决问题的过程中使创新思维得以提升

创新思维能力是当今社会对人才素质提出的必然要求，而以抽象概括性和超强的逻辑推理性著称的《高等数学》作为应用型本科院校的一门重要的基础课，在培养学生的创新思维方面起到了举足轻重的作用。

“带着问题来，带着问题走”的探究式课堂模式最大的特点是在授课过程中引导学生在不断解决问题的过程中达到对知识点的真正掌握。它通过教师和学生不断地提问、讨论和解答问题，充分调动了学生学习的积极性，而在解决各个问题的过程中，学生的逻辑思维能力和团结协作、解决实际问题的能力会逐渐提高，创新能力会慢慢加强，得以提升。

5 “带着问题来，带着问题走”的探究式课堂模式应用举例

下面进行“函数的极值，最值及其应用”课程设计。

5.1 课程设计的目的

理解函数的极值、最值的概念，掌握极值及最值的计算方法，会用极值和最值的知识解决一些实际问题。

5.2 设计内容

5.2.1 函数的极值及其求法

复习引入：

提问：全校长得最高的人和每个班级最高的人有什么区别？

全国范围内面积最小的城市和每个省面积最小的城市有什么区别？

答：全校长得最高的人和全国面积最小的城市都是整个研究范围内的最大最小值，而每个班级最高的人和每个省面积最小的城市都是局部的最大最小值。

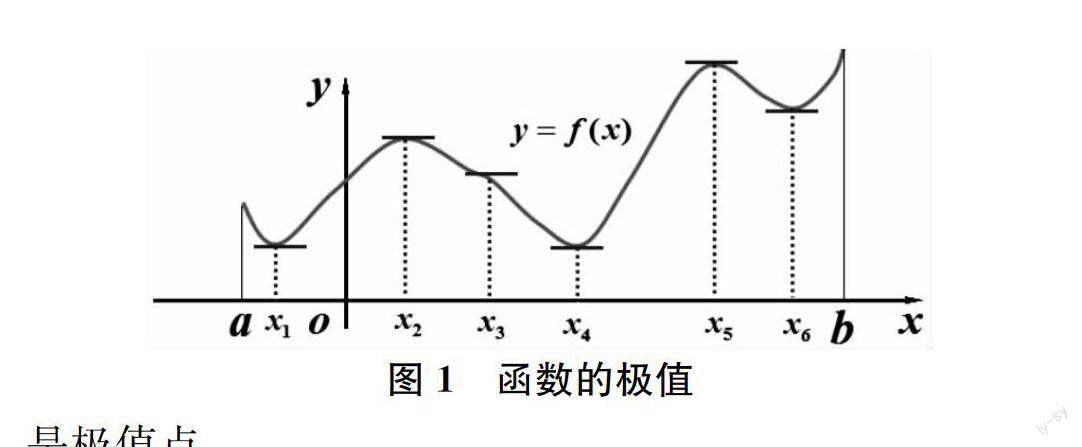
图1 函数的极值

定义：设函数f（x）在点x0的某邻域U（x0）内有定义，如果对于任意x∈U0（x0）有

f（x）f（x0）），则称f（x0）是函数f（x）的一个极大值（或极小值）。提问：f（a）和f（b）是极值吗？

答：不是。极值点应该是区间内部的点，边界点不是极值点。

观察与思考：极值与切线是什么关系？

极值的判定与求法：

定理（必要条件）：设函数f（x）在点x0处可导，且在x0处取得极值，那么f′（x0）=0。

讨论：（1）极值点是否一定是驻点？驻点是否一定是极值点？（2）曲线的升降与函数的极值间是什么关系？（3）考察x=0是否是函数y=x3的驻点，是否是函数的极值点？

定理（第一充分条件）：设函数f（x）在x0处连续，且在（a，x0）∪（x0，b）内可导，则：

（1）如果在（a，x0）内f′（x）>0，在（x0，b）内f′（x）<0，那么函数f（x）在x0处取得极大值。

（2）如果在（a，x0）内f′（x）<0，在（x0，b）内f′（x）>0，那么函数f（x）在x0处取得极小值。

（3）如果在（a，x0）及（x0，b）内f′（x）的符号相同，那么函数f（x）在x0处没有极值。讨论与思考：如何确定极值点并将其准确求出？

步骤如下：

（1）求出导数f′（x）；

（2）求出f（x）的全部驻点和不可导点；

（3）考察在每个驻点和不可导点的左右邻域f′（x）的符号；

（4）确定出函数的所有极值点和极值。

函数最值的求法

观察与思考：上图中如何求出闭区间[a，b]上函数的最大最小值呢？

步骤：

（1）求驻点和不可导点；

（2）求区间端点及驻点和不可导点的函数值，比较大小，最大值即为函数的最大

值，最小值即为函数的最小值。

5.2.2 最值的应用

引例：铁路上AB段的距离为100km，工厂C距A处20km，AB⊥AC，要在AB线上选定一点D向工厂修一条公路，已知铁路与公路每公里货运价之比为3∶5，为使货物从B运到工厂C的运费最省，问D点应如何选取？

讨论与思考：如何利用函数最值的知识解决引例中的问题呢？

一般实际问题转化为数学问题的步骤：

（1）建立目标函数；

（2）求最值；

（3）若目标函数只有唯一的驻点，则该点的函数值即为所求的最大（或最小）值。

模型建立：目标函数即总运费函数为：

y=5k202+x2+3k（100-x）（0

SymbolcB@ x

SymbolcB@ 100）

模型求解：y′=k（5x400+x2-3），令y′=0，得x=15，通过分析可知它是唯一的极小值点，故是最小值点。

作者简介：

唐红波（1982-），女，湖南东安人，本科学历，湖南东安职业中专讲师，研究方向：英语教育教学。