不同空间域七参数选取对坐标系转换的影响研究

引文格式： 田鑫，尹晖，干喆渊. 不同空间域七参数选取对坐标系转换的影响研究[J].测绘通报，2015(2)：10-13.DOI:10.13474/j.cnki.11-2246.2014.0031

不同空间域七参数选取对坐标系转换的影响研究

田鑫1，尹晖1，干喆渊2

(1. 武汉大学测绘学院, 湖北 武汉 430079； 2. 中国电力科学研究院，湖北 武汉 430074)

OntheEffectofCoordinateSystemTransformationbySelectingSeven

ParametersofDifferentSpatialDomain

TIANXin，YINHui，GANZheyuan

摘要：深入分析并论述了在小区域内用已知点解算出的七参数得到的转换坐标与用测绘部门给定的大区域七参数直接解算得到的转换坐标的差异，得出大区域转换七参数与小区域转换七参数转换坐标之间存在的关系。

关键词：区域转换七参数；坐标转换；WGS-84坐标系；1980西安坐标系

中图分类号：P228.4文献标识码：B

收稿日期：2014-02-14

基金项目：国家自然科学基金(51077105)；国家电网公司科技攻关团队项目(SG11013)；大地测量与地球动力学国家重点实验室开放基金(SKLGED2013-3-6-E)

作者简介：田鑫(1991—)，男，硕士生，从事GNSS数据处理的研究。E-mail:451128020@qq.com

一、引言

GPS以全天候、高精度、自动化和高效益等显著优势赢得了测绘工作者的信赖，并广泛应用于大地测量、工程测量、航空摄影测量、运载工具导航和管制、资源勘察、地球动力学等多学科领域[1-8]。但由于GPS测得的坐标是WGS-84坐标系下的，与我国主要采用1980西安坐标系下的坐标不同，因此在我国实际生产工作中，需要将GPS测得的WGS-84坐标转化为1980西安坐标系下的坐标。

七参数是实现不同的空间直角坐标系之间坐标转换的必要参数，包括3个平移参数、3个旋转参数和1个尺度参数[9-10]。七参数通常可以通过两种方式获得：①从测绘部门直接获得；②利用至少3个已知点求得。因此空间域大小的不同及七参数的选择问题都可能会影响坐标转换的精度，甚至准确度。本文基于布尔沙-沃尔夫(Bursa-Wolf)模型[11]，首先给出了坐标转换的主要公式，通过WGS-84坐标系与1980西安坐标系的转换实例，讨论了大小不同空间域七参数的选择对坐标转换结果的影响，分析了七参数的选择对转换坐标精度的影响关系。

二、 坐标转换

1. WGS-84空间直角坐标系转换为1980西安空间直角坐标系 [12]

布尔沙七参数模型可表示为

(1)

式中，(X1，Y1，Z1)为WGS-84空间直角坐标；(X2，Y2，Z2)为1980西安空间直角坐标；ΔX0、ΔY0、ΔZ0为3个平移参数；εX、εY、εZ为3个旋转参数；m为尺度参数。

2. 1980西安空间直角坐标系和1980西安大地坐标系之间的转换 [13]

大地经度L的计算公式为

(2)

大地纬度B的计算采用迭代法,步骤如下：

1) 设定初值B0

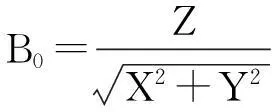
(3)

2) 迭代计算

(4)

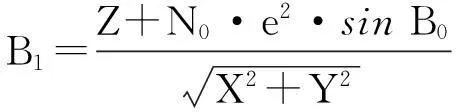
(5)

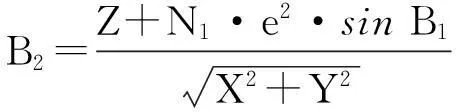
(6)

依此类推。

3) 设置结束计算条件为

(7)

4) 进行赋值

B=Bn或B=Bn-1

(8)

由大地坐标得到空间直角坐标公式为

(9)

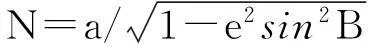
3. 高斯投影坐标正算 [12]

高斯投影坐标正算公式为

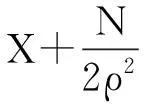
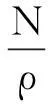
(10)

三、 实例试验与分析

1. 测区选择 [`14-15]

本次试验选择了两个测区开展研究。测区1位于泰安市南开发区，地形空旷，没有高大建筑物、大面积水域等，有利于GPS信号接收，在该测区内共布设了10个点位进行GPS观测，其中Z288、Z605和Z633为3个1980西安平面坐标系的已知点。测区2位于山东农业大学校本部，共选择了8个GPS控制点，其中A001 、A005和B014的1980西安平面坐标系的坐标已知，该测区同样没有高大建筑物、大面积水域等，也有利于GPS信号接收。相比泰安市7761km2面积而言，测区面积相对较小，表1给出了两个测区面积大小。

表1　测区面积

2. 数据采集

采集过程中同时观测有效卫星数≥6，PDOP值≤4，观测时段长度均大于1h，接收机与卫星间的图形强度良好，满足规范要求。

3. 数据处理与对比分析

数据处理主要包括GPS观测数据平差计算及坐标转换两部分。首先采用南方GPS数据处理软件对测区1实测的GPS数据进行处理，数据处理步骤包括：

1) 数据输入：将南开发区GPS外业观测数据的文件夹中的所有数据文件作为观测数据。

2) 基线解算：选择全部基线解算，并检查基线解算质量。

3) 输入已知点的坐标：将已知点Z288、Z605、Z633的1980西安平面坐标输入。

4) 平差处理：依次进行“自动处理”“二维平差”“三维平差”及“网平差计算”，得到10个测点在WGS-84坐标系下的平差坐标成果。

数据处理的第二部分是坐标转换，采用自编的坐标转换程序，并选择不同的七参数进行坐标转换。方式1：利用测绘部门给定的泰安市已知的大区域转换七参数将10个测点的WGS-84坐标转换为1980西安坐标系下的空间直角坐标，再投影到高斯平面，得到这10个测点的平面坐标。方式2：利用Z288、Z605和Z633这3个1980西安平面坐标系下的已知点解算得到七参数，将这10个测点的WGS-84坐标转化为1980西安空间直角坐标，再投影到高斯平面得到利用3个已知点解算的这10个点的高斯平面坐标。两种不同坐标转换方式得到的10个测点的坐标比较见表2。

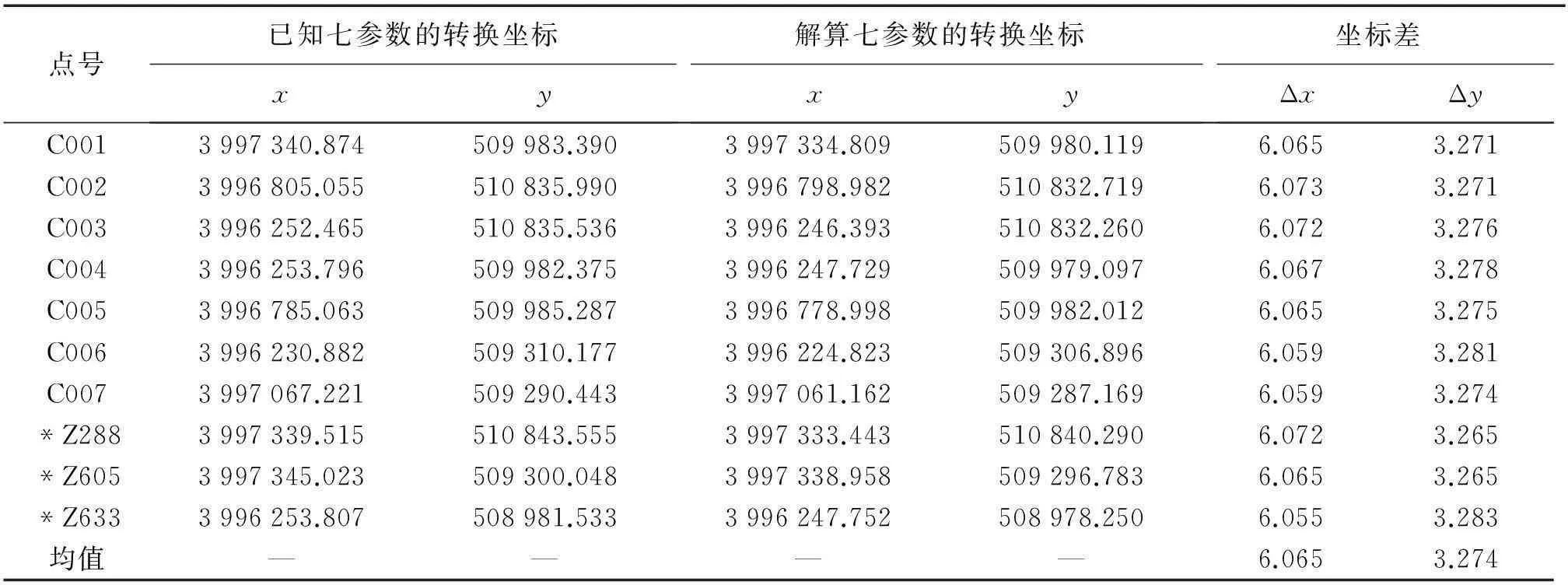
表2　南开发区转换坐标与解算坐标的坐标差　m

注：点号前标有“*”是解算七参数时使用的已知点。

同样，采用上述步骤和思路对测区2山东农业大学(校本部)8个测点GPS数据进行了平差处理及坐标转换，得到了两种不同方式坐标转换下8个测点的坐标比较，结果见表3。

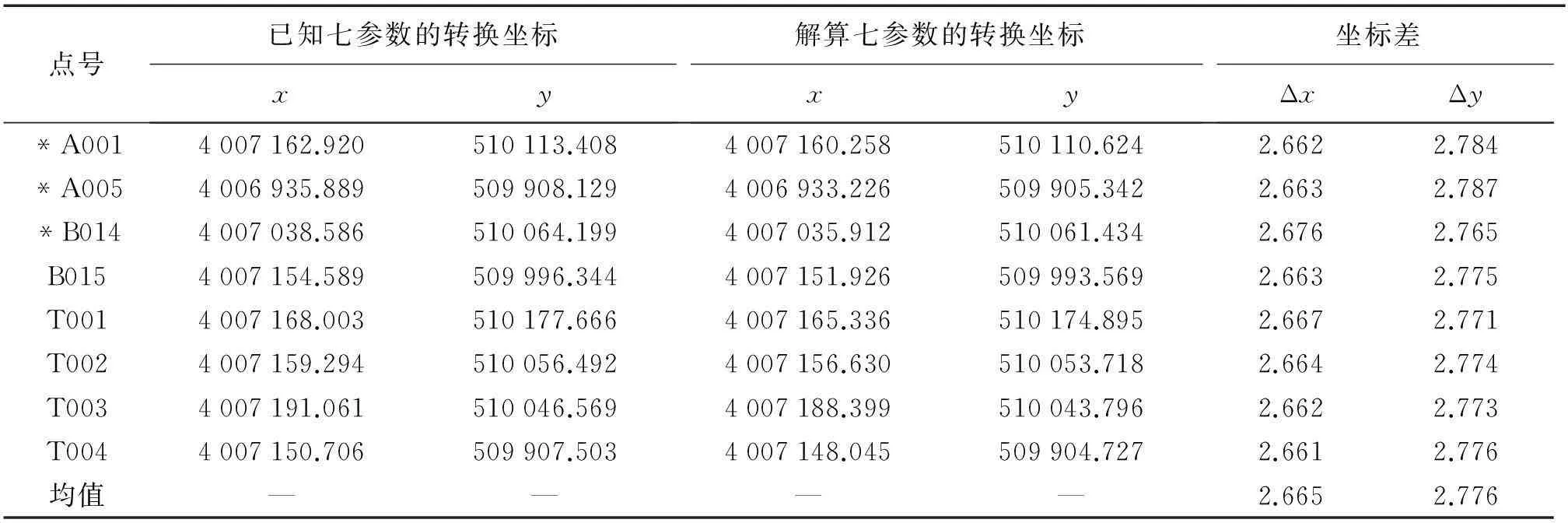
表3　山东农业大学校本部转换坐标与解算坐标的坐标差　m

注：点号前标有“*”是解算七参数时使用的已知点。

4. 假设无转换七参数的测量数据处理

直接将南方GPS数据处理软件平差后的WGS-84直角坐标当作1980西安直角坐标转换为高斯平面直角坐标，并分别与用3个已知点坐标经软件解算的结果相减，南开发区点位坐标差见表4，山东农业大学校本部点位坐标差见表5。

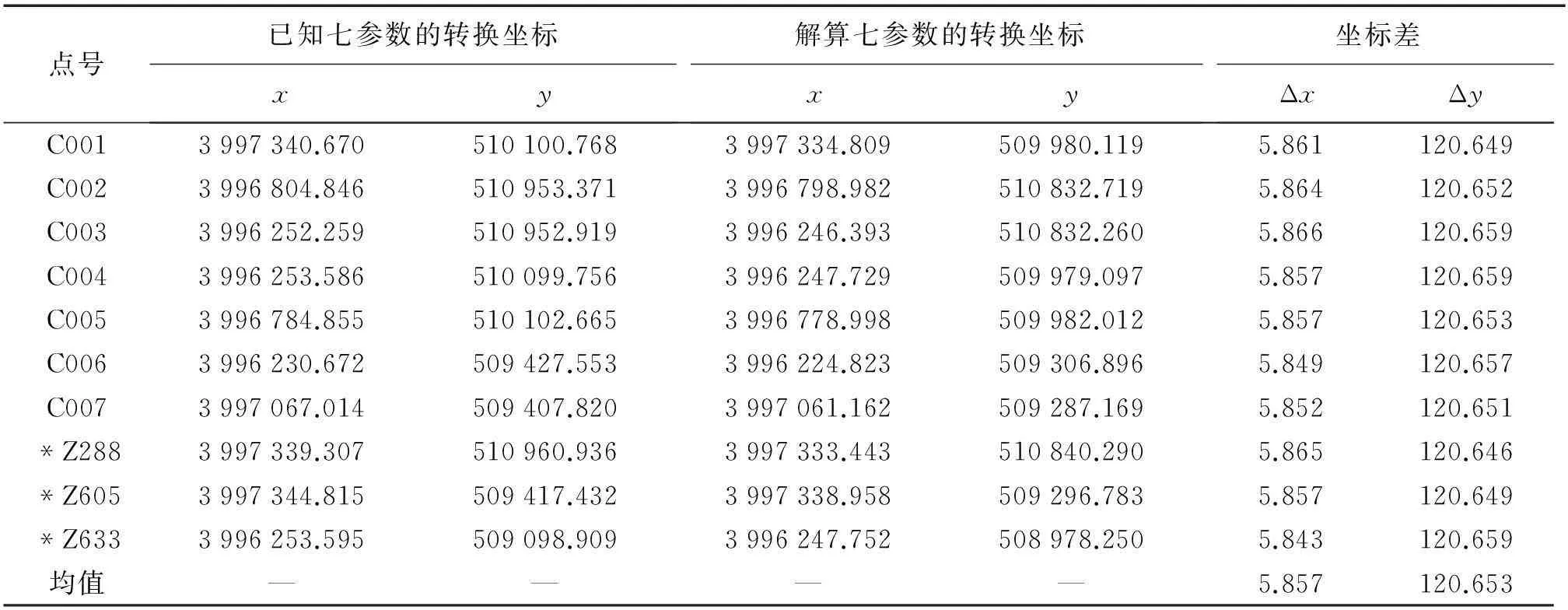
表4　南开发区无七参数转换坐标与解算坐标的坐标差　m

注：点号前标有“*”是解算七参数时使用的已知点。

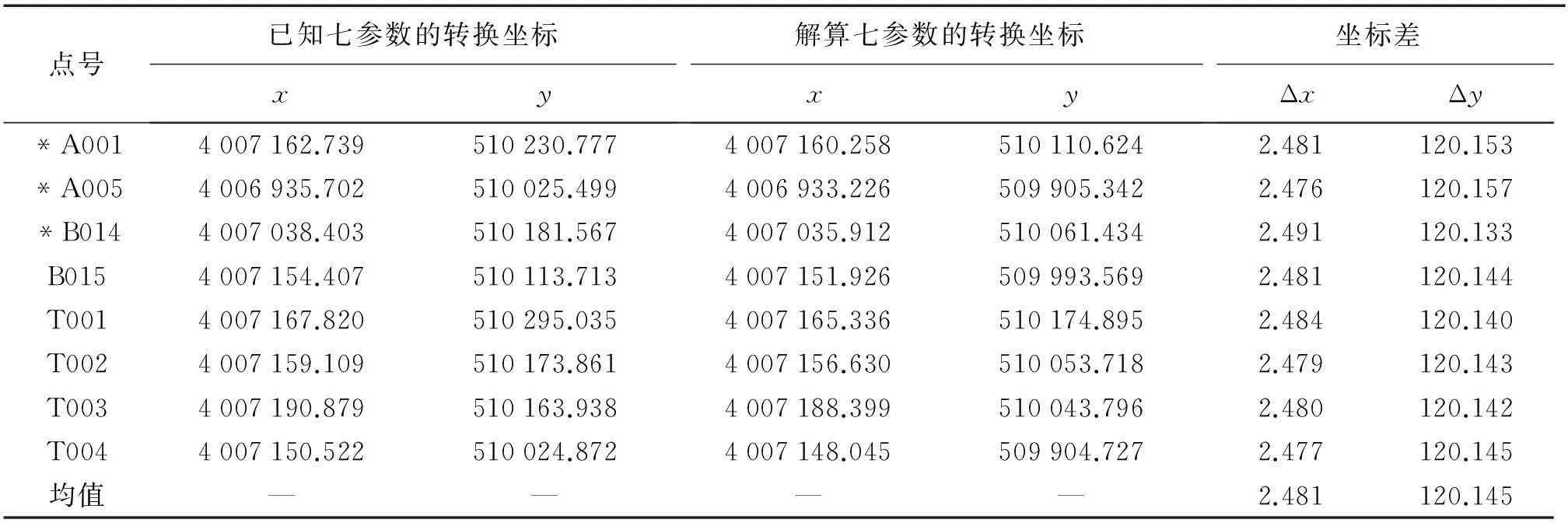
表5　山东农业大学校本部无七参数转换坐标与解算坐标的坐标差　m

注：点号前标有“*”是解算七参数时使用的已知点。

由表2和表3可以看出，用整个泰安市的坐标转换七参数转换得到的高斯平面坐标与在泰安地区小区域内用已知点解算得到的高斯平面坐标相差很大，而且坐标差值随区域的不同而不同。由表4和表5可以得出，大区域的转换七参数对于小区域内的坐标转换有一定的作用，但没有实际使用价值。

对比表2—表5可以得出，用整个泰安市的坐标转换七参数转换得到的高斯平面坐标与泰安地区小区域内用3个已知点解算得到的高斯平面坐标存在一组改正数，但改正数对于不同的区域也不同。

四、结论

通过对试验数据的正确处理及对以上整理的数据进行分析，可以得到如下结论：

1) 对小区域GPS观测结果进行WGS-84坐标系与1980西安坐标系的坐标转换，不应使用该小区域所属大区域的七参数转换得到，而应利用小区域内的已知点进行解算得到相应的转换七参数，然后再解算得到坐标。

2) 如果使用某一大区域中的WGS-84坐标系与1980西安坐标系的转换七参数转换其中小区域GPS观测值，所得结果与用该小区域3个(或3个以上)公共点解算得到七参数转换的坐标存在一组改正数(Δx，Δy)(忽略由于公共点的坐标存在误差及求得的转换参数所受的影响)，将大区域的WGS-84坐标系与1980西安坐标系的转换七参数转换结果加上改正数可得到该小区域的转换坐标。

参考文献：

[1]张项铎,谢世杰.WGS-84转换为国家实用坐标的研究[J].测绘通报,1997(5):5-7.

[2]成英燕，程鹏飞，秘金钟，等. 大尺度空间域下1980西安坐标系与WGS-84坐标系转换方法研究[J].测绘通报,2007(12)：5-8.

[3]郭春喜,马林波，张骥，等. 80西安坐标系与WGS-84坐标系转换模型的确定[J].东北测绘，2002,25(4):34-36.

[4]赵强国.使用七参数实现WGS-84经纬度坐标到80西安平面坐标的转换[J].安徽农业科学，2012(36)：68-70.

[5]王解先,王军等. WGS-84与北京54坐标的转换问题[J] .大地测量与地球动力学 ,2003,23(3)：70-73.

[6]施一民，冯琰.两种测地坐标系之间的坐标转换[J].测绘学报,2002 ,31(S0)：22-26.

[7]施一民，朱紫阳，范业明，等.新型大地坐标系与大地坐标系之间的转换[J].同济大学学报:自然科学版，2007,35(4):543-546.

[8]李冲,谭理，余银普，等.国家坐标与地方坐标的转换方法研究[J].城市勘测，2008(6):85-87.

[9]宫文学，李杨，王云男. 四参数法和七参数法坐标转换的比较[J]. 内蒙古科技与经济，2012(4)：109-110.

[10]谢鸣宇，姚宜斌. 三维空间与二维空间七参数转换参数求解新方法[J]. 大地测量与地球动学,2008，28(2)：104-109.

[11]孙小荣，张书毕，孙小荣，等. 七参数坐标转换模型的适用性分析[J]. 测绘科学，2012，37(6):37-39.

[12]孔祥元，郭际明，刘宗泉，等. 大地测量学基础[M].武汉：武汉大学出版社，2011.

[13]邱健壮.《大地测量学基础》辅助材料[M].泰安：山东农业大学测绘工程系，2009.

[14]徐绍铨，张华海.GPS测量原理及应用[M].武汉：武汉大学出版社，2008.

[15]李征航，叶乐安．沧州市GPS控制网的建立[J]．测绘通报，1991(4):14-19.