粒子群算法在非线性系统应用中的早熟现象及其改进

肖 媛, 崔国民, 彭富裕, 周 静（上海理工大学能源与动力工程学院,上海 200093）

粒子群算法在非线性系统应用中的早熟现象及其改进

肖 媛, 崔国民, 彭富裕, 周 静
（上海理工大学能源与动力工程学院,上海 200093）

通过分析粒子群算法早熟现象的机理,研究早熟收敛的本质,并提出一种克服粒子群算法早熟现象的局部“飞跃”策略.应用仿真及系统工程实例表明,该方法能有效地改善粒子群算法在非线性全局优化上的早熟问题,提高了粒子群算法的全局搜索能力.

粒子群算法；早熟收敛；系统工程；局部“飞跃”策略

0 引言

粒子群算法,也称粒子群优化算法（Particle Swarm Optimization,PSO）,是1995年Kennedy＆Eberhart[1]首次提出的模拟鸟类捕食行为的群体智能算法.Clerc＆Kennedy[2]对PSO的全局搜索能力、算法稳定性和收敛性能进行了理论分析,该算法具有易实现、收敛速度快、调整参数少的优点,且对于目标函数和约束条件的要求不高,为解决复杂非线性系统的优化问题提供了新的求解途径和方法,已经成功应用于系统工程的各个领域[3－9],并且在求解约束优化问题、离散优化问题和多目标优化问题等方面都得到了相应的发展.

然而,PSO存在早熟收敛的问题,尤其是在求解多维非线性问题时,会出现种群聚集到局部极值或局部极值邻域内的一个点停滞不动的现象.这一现象引起了国内外学者们的广泛关注,也对该缺陷作了改进尝试.Peram等[10]提出了FDR-PSO（Fitness-Distance-Ratio Based PSO）来改进粒子速度的更新模式,改善了早熟收敛现象；Peer等[11]提出了GCPSO（Guaranteed Convergence PSO）,利用不同的邻域拓扑结构来保持粒子搜索过程中的种群多样性,尽量避免其早熟收敛；刘华蓥等[12]提出了基于混沌优化搜索解决早熟收敛的粒子群算法,增强了粒子群算法的避免局部极小能力；吴敏等[13]提出了在粒子群收敛停滞时,通过引入共轭梯度算法计算的信息来影响粒子速度的更新以保持群体的活性；Chaturvedi等[14]提出了 SOH_PSO（selforganizing hierarchical PSO）,采用动态加速因子来增强种群多样性；魏建香等[15]提出了一种基于免疫选择的粒子群优化算法来调节种群的多样性；Sun等[16]提出了PSO-GSA（PSO with gravitational search algotithm）来平衡PSO的全局搜索能力和局部搜索能力,采用移动因子来改进速度更新公式而保持其种群多样性.以上的改进或是通过动态参数来活跃进化过程中的种群多样性,或是在粒子群收敛停滞后采用外部动力影响粒子的速度更新.然而应用到有约束、非线性的复杂系统的优化时,这一早熟现象还是没能从根本上得到解决,原因在于以上种种尝试尚未对PSO早熟的机理明确分析和解释,且无法克服优化问题本身的非线性而难以实现进化后期局部极小值的逃离.

本文通过分析PSO在复杂非线性系统进化的特点,及其在不同局部最优解周围的进化进程,揭示粒子群算法进化后期局部退化现象的原因和机理；在此基础上,提出克服进化后期早熟的局部“飞跃”策略,使停滞收敛的粒子获得“重生”,力图完善粒子群算法的全局搜索能力.

1 PSO早熟退化现象及其分析

1.1 PSO的数学模型

粒子群算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解,群体由N个粒子组成,每个粒子代表了搜索空间中一组d维潜在解,包括当前位置xi＝（xi1,xi2,…,xid）和当前飞行速度vi＝（vi1,vi2,…,vid）,i＝1,2,…,N.在每次迭代中,粒子通过追踪两个“经验”来调整下一次迭代的位置和速度,这两个“经验”就是个体极值pi＝（pi1,pi2,…,pid）和种群的全局极值pg＝（pg1,pg2,…,pgd）.粒子根据自身惯性vi、个体极值pi、种群极值pg更新飞行的速度和位置：

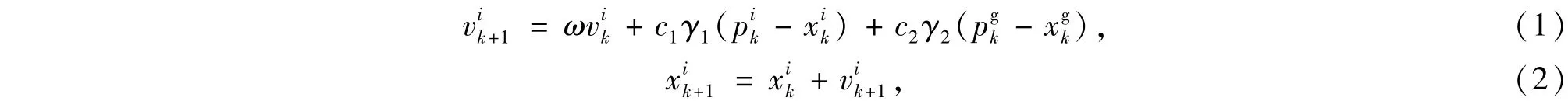
式中,惯性因子ω是非负常数,学习因子c1和c2是非负常数,γ1和γ2是取值介于（0,1）的伪随机数,k是迭代次数.

式（1）中的第一项表示粒子对其历史信息的“遗传”,ω控制了算法的开发和控制能力,当ω较大时可扩展粒子的搜索空间,增强算法的全局寻优能力,当ω较小时算法的局部搜索能力得以改善；后两项表示粒子对自身经验的认知及粒子之间的信息共享和相互作用,可认为是PSO优化过程中的“进化项”.粒子更新模式如图1所示.进化初期,每个粒子的位置和速度是随机初始化的,种群中的最优粒子pg吸引其它结构,使种群中的大部分粒子在“进化项”的作用下快速聚集到全局最优区域[17].因此,粒子群算法具有较强的全局搜索能力,且在进化初期收敛速度较快.

1.2 PSO的早熟收敛的机理分析

通过实例发现在求解多维复杂非线性问题时,PSO容易陷入早熟收敛.文献[12]引入了早熟收敛判断机制,利用种群适应度方差σ2来反映粒子的聚集程度,σ2越小,粒子聚集程度越大,若此时算法不满足约束条件,将使种群失去多样性而陷入早熟状态.因此当σ2＜c（c为给定常数）时,必须进行早熟处理,以避免优化陷入局部极小值.为了实现种群跳出早熟收敛,首先必须分析PSO早熟的机理,探寻其搜索能力退化的本质.为简化分析,本文以二维粒子为例,将粒子飞行速度的更新表示在二维直角坐标系如图2.

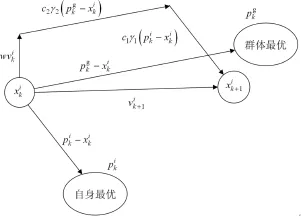
图1 粒子群算法更新模式Fig.1 Updatemode for PSO

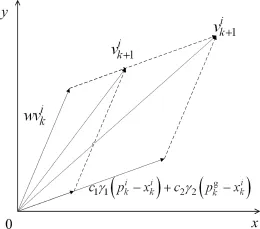
图2 二维粒子更新示意图Fig.2 Velocity update of particle for d＝2

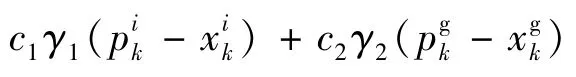
2 局部“飞跃”策略

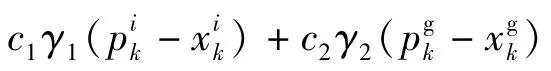
为了改进PSO的局部退化现象,必须激活进化后期停滞的粒子,使粒子飞行获得“重生”,恢复种群的多样性,本文提出一种局部“飞跃”策略,当PSO陷入停滞时,对式（2）中的xik＋1在当前局部极值点对应的x∗

k的邻域范围内给予一个新的随机量,而不再按照先前的寻优方向搜索,进而随机搜索到更优解.当粒子搜索到更优解,以搜索到的该解作为PSO下一轮搜索的初始点,强制跳出极小值点,并继续搜索全局最优解.引入早熟收敛判断及局部“飞跃”策略的粒子群算法流程图如图3.

图3 引入早熟收敛判断及局部“飞跃”策略的PSO流程图Fig.3 Flow chart of PSO with premature judgement and“leap”handling strategy

局部“飞跃”策略充分利用了随机变量的随机性、遍历性以及PSO的开放式结构特点,对优化问题的目标函数要求不高,无须优化问题具有连续性和可微性,因此采用该策略解决PSO优化复杂非线性系统中的早熟收敛问题,在局部极值的邻域范围随机搜索以在解空间找到更优值作为PSO下一次迭代的初始点.

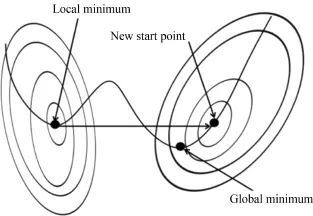
图4 粒子随机搜索示意图Fig.4 Stochastic search pattern of particles trapped into localminimum

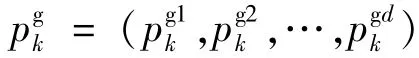
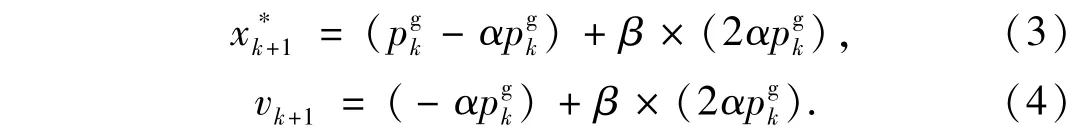
3 实验仿真与实例分析

3.1 Benchmark测试函数

选取Rastrigin函数、Griewank函数作为Benchmark测试函数,函数的名称、公式、维数、范围、目标最小值如表1.

两种函数均属于多峰非线性函数,搜索空间大,局部极值点多,一般算法难以找到其全局最优解,因此可以用来检验改进前后的粒子群算法跳出局部最优的能力.为了保证算法的收敛,惯性因子ω取0.9,学习因子c1和c2均取0.5.在进行算法仿真时,改进前后的PSO的迭代次数均为1 000,其它参数设置均相等.

表1 Benchm ark函数Table 1 Benchmark functions

首先,以二维函数的仿真来研究初始点对粒子群算法优化效能的影响,如图5和图6.对于Rastrigin函数,标准PSO基本都能找到目标最小值0,但当初始点偏离全局最优点较远时,PSO优化仍会陷入早熟,优化结果为0.994 954 425 017 109.对于非线性更强的Griewank函数,初始点距离全局最优区域越远,PSO仿真结果偏离目标最小值越大,只有在（－1,1）范围内才能准确搜索到目标最小值.

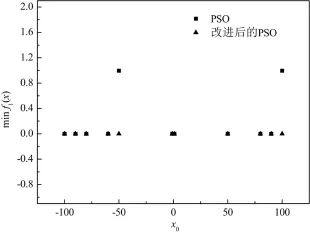
图5 Restrigin函数仿真中初始点对优化结果的影响Fig.5 Effect of initial point on optimization result in Restrigin function

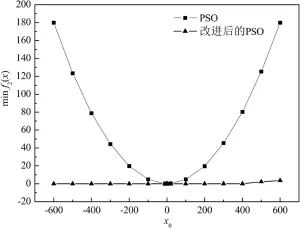
图6 Griewank函数仿真中初始点对优化结果的影响Fig.6 Effect of initial point on optimization result in Griewank function

针对PSO在非线性系统优化中的早熟收敛现象,引入局部“飞跃”策略,极大地解决了PSO进化后期陷入局部极值点的问题,增强了PSO的全局搜索能力,提高了算法的优化精度.对Restrigin函数的仿真均找到了全局最优解,如图5.对于Griewank函数,从图6中发现,当初始点在（－600,493）范围,改进后的PSO算法克服了标准PSO的早熟收敛,准确搜索到了目标最小值；当初始点在（494,600）范围,改进后的PSO仿真结果相较目标最小值仍有较小的偏离,其原因在于目标函数的复杂非线性而难以找到全局最优解.

其次,维数越高,PSO算法的早熟收敛现象越明显,对10维、15维、20维的Rastrigin函数和Griewank函数采用PSO、改进后的PSO进行仿真实验,在定义域范围内随机生成相同的初始结构,参数设置同上,实验结果如表2.

表2 多维测试函数的仿真结果Table 2 Results of benchmarks w ith different dimensions

15维的Rastrigin函数的仿真收敛曲线如图7,显示了引入局部“飞跃”策略的PSO算法跳出局部极小值并搜索到全局最优解的过程,验证了该策略能有效地解决PSO在非线性系统优化中的早熟问题.

3.2 系统工程实例

换热网络优化是过程系统工程中的重要领域,对系统能量的有效利用起着至关重要的作用.换热网络综合就是要使热回收目标最大或者费用目标最小,该问题本质上属于混合整数非线性规划[18],其非线性主要源于对数平均温差及费用计算时的非线性项,而表示换热器有无的整型变量又极大地增加了非线性的复杂程度[19],因此即使小规模换热网络也无法证实能够找到其全局最优解[20].PSO应用到换热网络优化过程中,还是经常出现飞行速度退化而使算法陷入早熟收敛的问题.本文将改进前后的PSO应用于换热网络优化算例,惯性因子取0.9、学习因子均取0.5,选取文献中的固定结构进行连续变量的优化,通过实例分析PSO应用于复杂非线性系统的早熟收敛问题,并验证以上局部“飞跃”策略的有效性.

10SP2算例流体参数取自文献[21],换热器、冷却器和加热器的传热系数均为0.025 kW·（m2·℃）－1,换热器面积计算公式为60A ＄·year－1,热公用工程费用为100＄·（kW·year）－1,冷公用工程费用为15＄· （kW·year）－1,其它物流参数见表3.

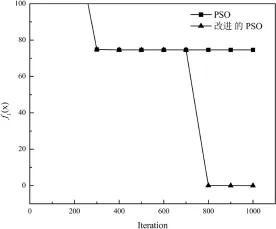
图7 Rastrigin函数的仿真收敛曲线对比Fig.7 The contrastive convergence cuves of simulation for Rastrigin fuction

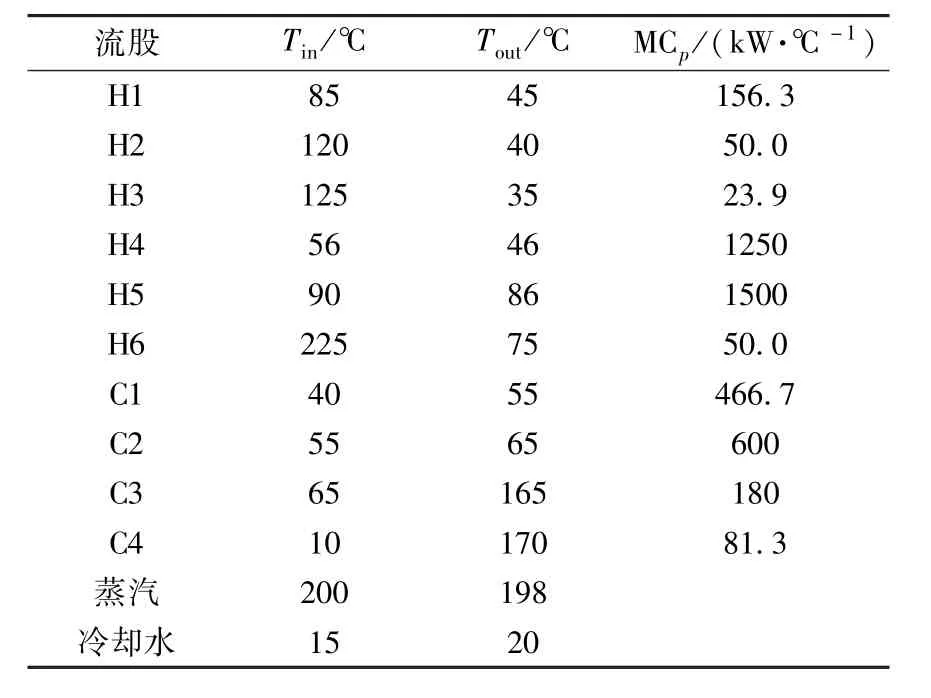
表3 10SP2算例流体参数表Table 3 Fluid parameters for case 10SP2

文献[21]中采用遗传算法优化得到换热网络最小年综合费用5 666 755＄·year－1,对文献[21]的换热网络结构采用粒子群算法优化得到的最小年综合费用为5 641 344＄·year－1,其费用－迭代次数折线图如图8.进化初期,年综合费用快速下降,但在进化后期趋于平稳,保持在5 641 344＄·year－1.由早熟收敛判断机制可知,当前PSO的优化费用是局部极小值而非全局最优解,即此时的收敛属于早熟现象.

为了使种群快速跳出早熟收敛,引入上文提出的改进策略,在局部极小值的邻域范围内随机搜索,如图3进行迭代计算,并增加迭代次数,扩大随机搜索的空间,得到了新的费用下降曲线.将两次的费用下降曲线对比如图9,从图中可明显看出局部“飞跃”策略有效地处理了粒子群的早熟收敛问题,多次跳出了局部极小值点,最终得到的最小年综合费用为5 640 721＄·year－1,对应的换热网络结构的能量分布如图10,本文的优化费用与文献对比结果如表4.

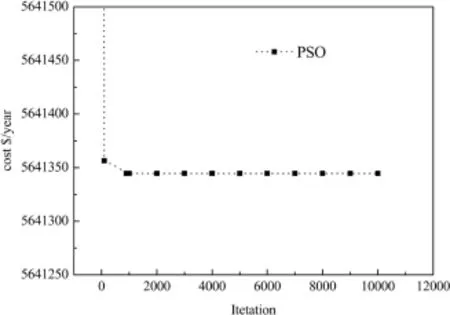
图8 对文献[21]中的结构进行PSO优化得到的费用－迭代次数折线图Fig.8 Decline curve of 10SP2 in Ref.[21]for PSO

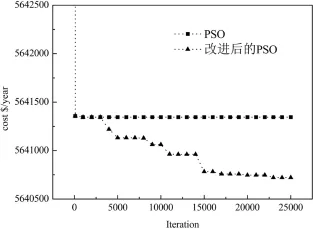
图9 改进前后的PSO优化费用下降对比图Fig.9 Contrastive decline curves of10SP2 for PSO with and without improvement

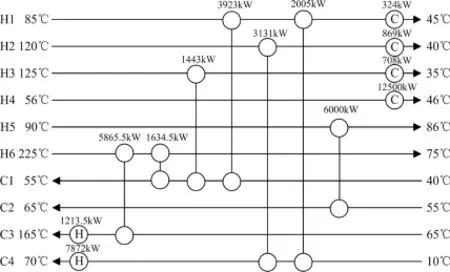
图10 对文献[21]采用结合局部“飞跃”策略的PSO算法优化后的换热网络结构Fig.10 HEN structure of improved PSO in Ref.[21]

文献[21] 标准PSO 文献[22] 本文5 666 755＄·year－1 5 641 344＄·year－1 5 640 730＄·year－1 5 629 721＄·year－1

图11 PSO优化的费用下降曲线Fig.11 Decline curve of10SP2 for PSO

文献[23]采用局部优化方法得到的最小年综合费用为5 631 380＄·year－1,对文献[23]对应的换热结构采用粒子群算法优化后费用为5 632 308＄·year－1,其费用－迭代次数折线图如图11.粒子群算法在进化初期收敛速度快,费用下降快,但在进化后期趋于平稳,费用保持在5 632 308＄·year－1,对比文献[23]得到的5 631 380＄·year－1可知,当前PSO的优化费用是局部极小值而非全局最优解,即此时的收敛属于早熟现象.

引入本文提出的局部“飞跃”策略,在局部极小值的邻域范围搜索,最终多次跳出了局部极值点,而得到了更优换热网络结构,其能量分布如图12.改进前后的费用下降对比曲线图如图13,本文的优化费用与文献对比结果如表5.从费用下降曲线能明显地看出粒子跳出局部极小值的“重生”过程,验证了局部“飞跃”策略的有效性.

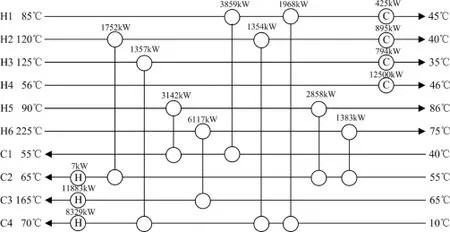
图12 对文献[25]采用结合局部“飞跃”策略后的PSO算法优化后的换热网络结构Fig.12 HEN structure of improved PSO in Ref.[25]

表5 文献[23]算例优化结果对比Table 5 Results com parison w ith 10SP2 in Ref.[23]

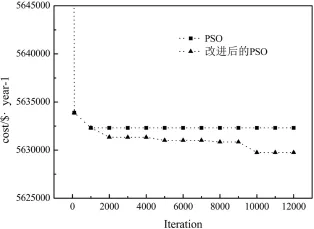
图13 改进前后的PSO优化费用下降对比图Fig.13 Contrastive decline curves of 10SP2 for PSO with and without improvement

4 结论

改进PSO在复杂非线性系统应用中的早熟收敛,提出了局部“飞跃”策略的PSO算法,增强了PSO的全局搜索能力.通过Benchmark测试函数仿真验证,引入局部“飞跃”策略的PSO具有更大的全局搜索区域,使Griewank函数的全局搜索区域从 （ －1,1）扩大到 （－600,493）；对于严重非线性的换热网络优化问题,通过10SP2算例验证,改进的PSO跳出了标准PSO进化后期陷入的局部极小费用,重新分配了换热网络的能量分布,使换热网络性能均得到了一定的提升.

[1] Kennedy J,Eberhart R.Particle swarm optimization[C]∥1995 IEEE International Conference on Neural Nerworks Proceedings.Perth：IEEE,1995：1942－1948.

[2] Clerc M,Kennedy J.The particle swarm-explosion,stability,and convergence in a multidimensional complex space[J].Evolutionary Computation,IEEE Transactions on,2002,6（1）：58－73.

[3] Abido M.Optimal design of power-system stabilizers using particle swarm optimization[J].IEEE Transactions on Energy Conversion.2002,17（3）：406－413.

[4] Yoshida H,Kawata K,Fukuyama Y,Takayama S,Nakanishi Y.A particle swarm optimization for reactive power and voltage control considering voltage security assessment[J].IEEE Transactions on Power Systems,2000,15（4）：1232－1239.

[5] Zhang JR,Zhang J,Lok T M,Lyu M R.A hybrid particle swarm optimization-back-propagation algorithm for feedforward neural network training[J].Applied Mathematics and Computation,2007,185（2）：1026－1037.

[6] Zhang X,Yu L,Zheng Y.Two-stage adaptive PMD compensation in a 10 Gbit/s optical communication system using particle swarm optimization algorithm[J].Optics Communications,2004,231（6）：233－242.

[7] Liu HW,Li J.A particle swarm optimization-based multiuser detection for receive-diversity-aided STBC systems[J].Signal Processing Letters,2008,15：29－32.

[8] Silva A P,Ravagnani M A S S,Biscaia Jr E C,et al.Optimal heat exchanger network synthesis using particle swarm optimization[J].Optimization and Engineering,2010,11（3）：459－470.

[9] Gudise V G,Venayagamoorthy G K.FPGA placement and routing using particle swarm optimization[C]∥IEEE Computer Society Annual Symposium on VLSI：Emerging Trends in VLSISystems Design,Lafayette,LA,USA,2004：307－308.

[10] Peram T,Veeramachaneni K,Mohan C K.Fitness-distance-ratio based particle swarm optimization[C]∥Swarm Intelligence Symposium,2003.SIS'03.Proceedings of the 2003 IEEE.IEEE,2003：174－181.

[11] Peer E S,Van den Bergh F,Engelbrecht A P.Using neighbourhoods with the guaranteed convergence PSO[C]∥Swarm Intelligence Symposium,2003.Proceedings of the 2003.IEEE,2003：235－242.

[12] Liu Huaying,Lin Yuer,Zhang Junshi.A hybrid particle swarm optimization based on chaos strategy to handle local convergence[J].Computer Engineering,2006,42（13）：77－79.

[13] Wu Min,Ding Lei,Cao Weihua,et al.A kind of hybrid optimization algorithmwith prevention of premature convergence of particleswarm[J].Control and Decision,2008,23（5）：511－514.

[14] Chaturvedi K T,Pandit M,Srivastava L.Self-organizing hierarchical particle swarm optimization for nonconvex economic dispatch[J].Power Systems,IEEE Transactions on,2008,23（3）：1079－1087.

[15] W Jianxiang,SYuehong,SXinning.A novel particle swarm optimization based on immune selection[J].Journal of Nanjing University（Natural Science）,2010,46（1）：1－9.

[16] Sun S,Peng Q.A hybrid PSO-GSA strategy for high-dimensional optimization andmicroarray data clustering[C]∥Information and Automation（ICIA）,2014 IEEE International Conference,2014：41－46.

[17] Kennedy J.Smallworlds and mega-minds：Effects of neighborhood topology on particle swarm performance[C]∥Evolutionary Computation,1999.Proceedings of the 1999 Congress IEEE,1999：3.

[18] Yee T F,Grossmann IE.Simultaneous optimizationmodels for heat integration（II）：Heatexchanger network synthesis[J].Compute Chem Eng,1990,14（10）：1165－1184.

[19] Hu Xiangbai,Cui Guomin,Tu Weimin.The non-linear characteristics analyze of the minlp in the complex heat exchanger networks[J].Journal of Engineering Thermophysics,2012,33（002）：285－287.

[20] Yerram setty K M,M urty C V S.Synthesis of cost—optimal heat exchanger networks using differential evolution[J].Computers and Chemical Engineering,2008,32（8）：1861－1876.

[21] RavagnaniM,Silva A P,Arroyo PA,et al.Heat exchanger network synthesis and optimization using genetic algorithm[J].Applied Thermal Engineering,2005,25（7）：1003－1017.

[22] He Qiaole,Cui Guomin,Xu Haizhu.Application of memetic particle swarm optimization to continuous variable global optimization of cost-optimal heat exchanger networks[J].Petrochemical Techonology,2014,（1）：37－45.

[23] Hu Xiangbai.Global synthesis of heat exchanger networks[D].Shanghai：Journal of University of Shanghai for Science and Technology,2013.

An Im proved Particle Swarm Optim ization for Precocious Phenomenon in Nonlinear System Engineering

XIAO Yuan, CUIGuomin, PENG Fuyu, ZHOU Jing
（School ofEnergy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China）

By analyzingmechanism of premature phenomenon in particle swarm optimization（PSO）,we found nature of premature convergence and proposed a“leap”strategy to jump out of localminimum,making halted particles“renewed”when they are trapped into a local optimum.The strategy is applied to nonlinear programming and results are encouraging.The improved PSO solves efficiently premature convergence of the algorithm applying in nonlinear optimizations and improves global search ability of PSO.

particle swarm optimization；premature converge；systems engineering；“leap”strategy

1001-246X（2015）06-0693-08

TP18

A

2014－11－11；

2015－04－14

国家自然科学基金（51176125）及沪江基金研究基地专项（D14001）资助项目

肖媛（1991－）,女,硕士研究生,研究方向为过程系统工程,E-mail：yxiao0606＠yeah.net