基于二维模糊控制的汽车智能限滑系统的研究
2015-12-31骆艳洁丁荣莉
李 骁,骆艳洁,贺 锐,丁荣莉
(上海理工大学 机械工程学院,上海 200093)
0 引言
为保证较高的通过性,越野汽车一般采用四轮驱动方式,以便使车辆获得更好的轮胎牵引力。但由于差速器的作用,当一个车轮打滑时,该车轮会大量地消耗发动机输入功率,造成四轮驱动汽车在湿滑的坡道路面上因失去轮胎牵引力而丧失通过能力。针对此情况,本文建立了汽车传动系统总模型,提出了采用二维模糊控制器进行控制的智能限滑系统方案,较好地解决了上述问题。
1 基于二维模糊控制的汽车智能限滑系统
汽车智能限滑系统的控制框图如图1所示,当没有车轮打滑时,车轮转速差只是用于满足车辆转向行驶时的差速要求,此时检测到车轮转速差小于设定值a,控制器的制动力矩信号输出为0,汽车正常行驶。
当有车轮发生打滑时,轮速差超过设定值a,该系统开始工作,扭矩传感器检测打滑车轮上的驱动扭矩值,并以此作为制动力矩的主值,而模糊控制器根据当前的车轮转速差和车轮驱动扭矩计算出校正制动扭矩用来微调和修正主值,最终分配到打滑的车轮上。调整到轮速差小于b时,系统自动关闭。
图1中,U为模糊控制器输出,R为传统系统输入,Y为传动系统输出,a为系统启动设定值,b为系统关闭设定值,ωL、ωR分别为左、右两个车轮的转速,M滑为打滑车轮上的驱动扭矩值。
2 传动系统模型的建立
只考虑变速器速比ig、主减速器速比i0和传动系效率η的影响,变速器和主减速器的动力学方程为[1]:
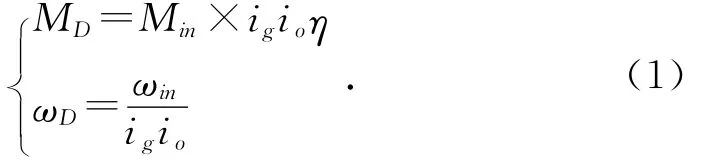
其中:MD为汽车差速器壳输入扭矩;Min为汽车发动机输出扭矩;ωin为发动机输出转速;ωD为差速器壳转速。

图1 汽车智能限滑控制系统流程方框图
差速器动力学方程为:
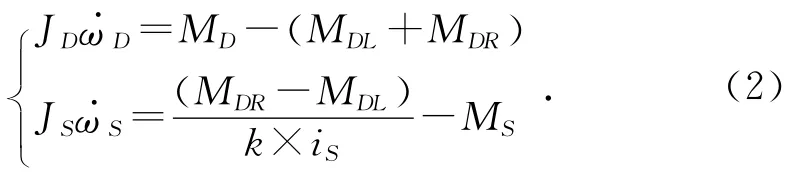
其中:ωS为行星轮相对差速器壳的转速,rad/s;JD为差速器壳绕自转轴转动惯量,kg·m2;JS为单个行星轮绕自转轴转动惯量,kg·m2;MDL、MDR分别为左、右驱动轮上的驱动力矩,N·m;iS为差速器行星齿轮与驱动轴齿轮副传动比;k为行星齿轮个数;MS为行星轮轴上的摩擦力矩,N·m。
差速器壳转速ωD及行星轮相对差速器壳的转速ωS与左右驱动轮转速ωL、ωR间的关系为[2-3]:
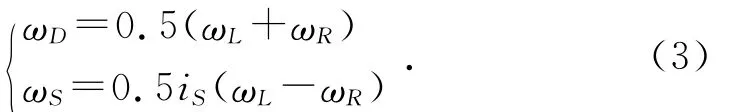
假设左边车轮打滑,根据汽车驱动过程中驱动车轮的受力分析,取车轮前进方向为正,可知:
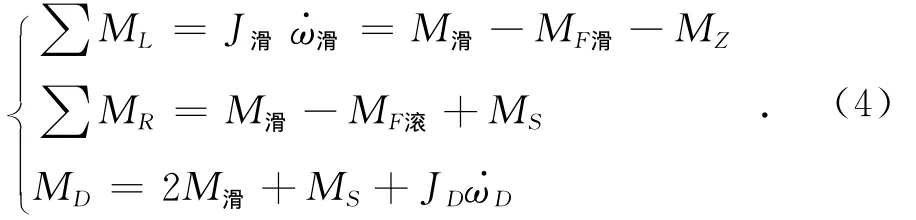
其中:ML、MR为左、右车轮所受扭矩;J滑为打滑车轮的转动惯量;ω滑为打滑车轮转速;MZ为制动器制动力矩;MF滚为非打滑车轮受到的滚动摩擦力矩;MF滑为非打滑车轮受到的滑动摩擦力矩。
汽车驱动存在单轮打滑过程中,打滑与非打滑车轮的转速关系为:
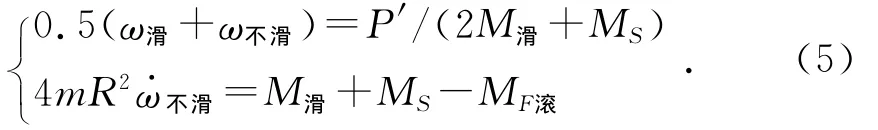
其中:P′为传到差速器壳体上的发动机功率;R为车轮半径;m为汽车质量;ω不滑为非打滑车轮转速。
在智能限滑系统处于启动状态,将式(1)、式(3)代入式(2)、式(4)、式(5)中,并联立式(2)、式(4)、式(5)得到以发动机功率P和制动扭矩MZ为输入的系统动力学方程:
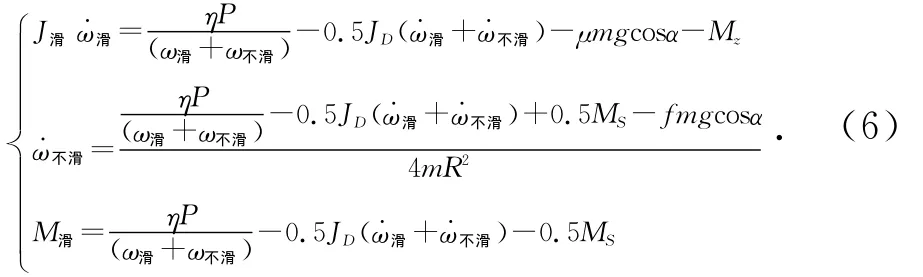
其中:MZ=U+M滑,U为二维模糊控制器输出的制动扭矩值;μ为滑动摩擦因数;f为滚动摩擦因数;α为路面与水平面之间的倾角。
3 二维模糊控制器的设计
3.1 二维模糊控制器的结构
图2为二维模糊控制器结构框图[4],将轮速传感器采集的同轴上两轮的轮速差E和发动机当前传到打滑轮的驱动扭矩Em作为二维输入变量,U1为模糊控制器1的输出量,U2为模糊控制器2的输出量,作为累加器C2的累加量。
图2中,Ka、Kb、Kc、Kd为各输入量的模糊量化因子。
3.2 输入输出语言变量及其模糊化
设定转速差的模糊控制区[-emax,emax]为E=[-15,15],转速差变化率的模糊控制区[-ecmax,ecmax]为Ec= [-5,5]。设定驱动扭矩的模糊控制区为Em=[0,1 500]。设定模糊论域为mamdani论域[5],其中fuzzy1中的模糊论域与模糊子集设定如下:E,Em={-3-2-1 0+1+2+3};E={NL NM NS Z PS PM PL};Em={NL NM NS Z PS PM PL};fuzzy2中的模糊论域与模糊子集设定如下:E,Ec={-3-2-1 0+1+2+3};E={NL NM NS NZ PZ PS PM PL};Ec={NL NM NS Z PS PM PL}。
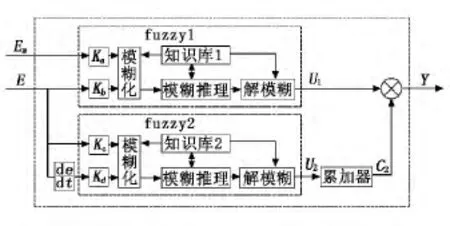
图2 二维模糊控制器结构
经反复仿真调试优化,定义出E、Ec和Em的隶属度函数定义曲线,其中NL采用Z函数,PL采用S函数,其余采用三角型函数。
设定fuzzy1输出制动扭矩信号控制范围U1=[-300,300],fuzzy2微调累加信号值输出控制范围U2=[-6,6]。基于输入变量模糊化的设定及实际模糊控制规则的需要,设定输出U的论域和模糊子集为:U1,U2={-3-2-1 0+1+2+3};U1,U2={NL NM NS Z PS PM PL}。
3.3 模糊控制规则及算法结构设计
该控制器通过两个模糊推理机混合推理计算对扭矩传感器输出的制动扭矩主值进行修正,fuzzy1根据当前汽车车轮轮速差E与打滑车轮上的驱动扭矩Em值,算出一个与当前制动扭矩主值相适应的静态修正值U1(相当于P校正);而fuzzy2根据当前的偏差值E与偏差变化率Ec,求出一个累加量U2(相当于I校正),作为U1的超前微调量,不断对U1进行微量修正。根据以上控制思想,并经反复调试验证,定义控制器fuzzy1和fuzzy2的模糊规则如表1、表2所示。
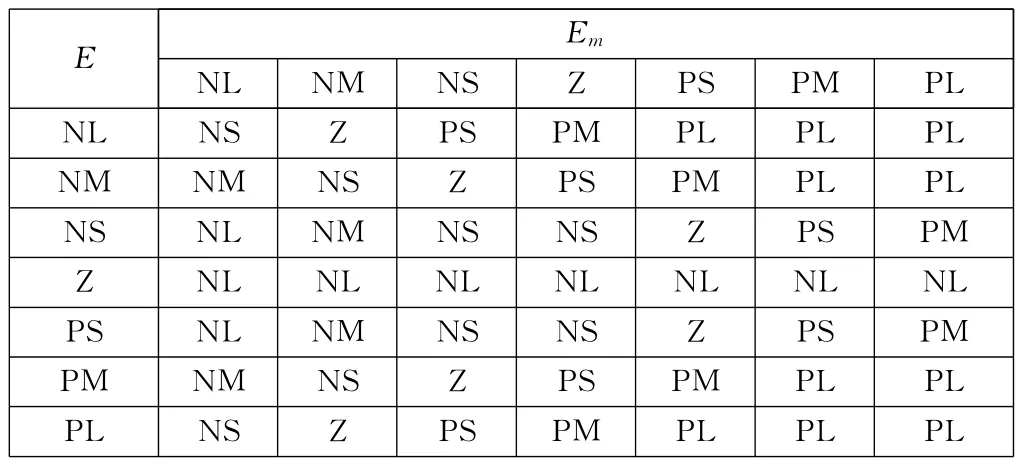
表1 fuzzy1模糊规则表(U1)
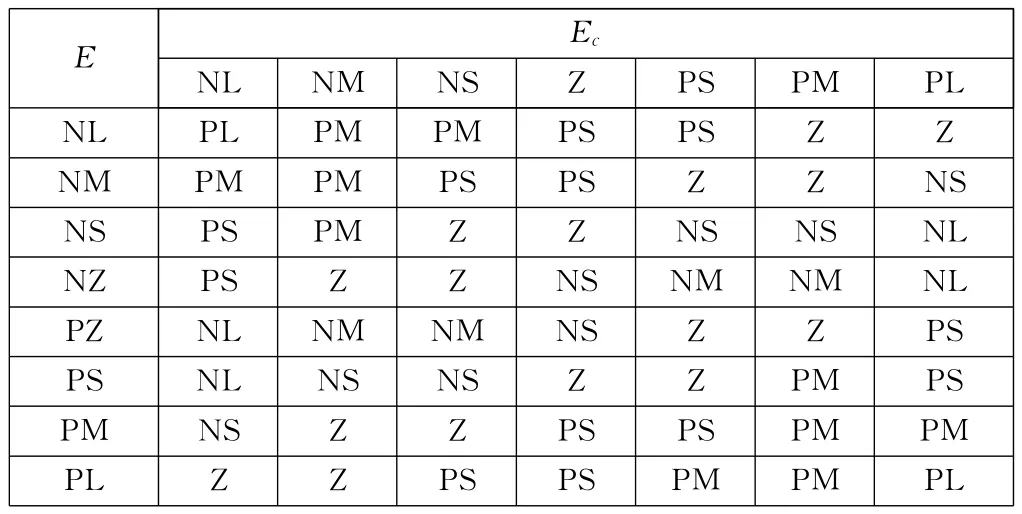
表2 fuzzy2模糊规则表(U2)
经过mamdani最小推理机得到的控制量是一个模糊向量,采用加权平均法解模糊,则由在其论域上的精确输出和经过量化因子反变换得到的实际模糊控制器输出值为:
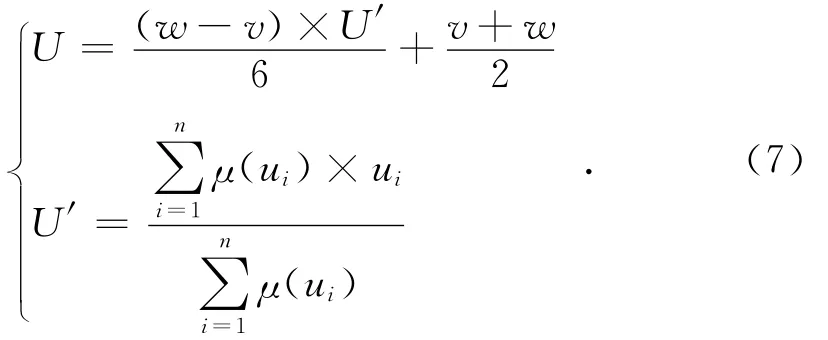
其中:μ(ui)为模糊控制量输出在其各模糊集上的隶属度;v、w为模糊论域边界值。
模糊控制器总输出为:

模糊控制器信号输入与扭矩信号输出关系如图3所示,图3(a)中横坐标为转速差E与打滑车轮上的驱动扭矩Em,纵坐标为制动控制校正信号输出U1;图3(b)中横坐标为轮速差E与轮速差变化率Ec,纵坐标为微调校正信号输出U2。可见二维模糊控制器对转速差、轮速差变化率和打滑车轮上的驱动扭矩信号的分析和叠加输出控制可对制动主值进行精确修正。
4 结论
本文提出的基于二维模糊控制的智能限滑分矩系统结构简单,易于根据不同车型与实际测试结果调校控制范围和优化模糊控制规则,可以较好地解决因单侧车轮打滑导致整车丧失地面牵引力而造成车辆无法行驶的问题,有一定的运用与推广价值。
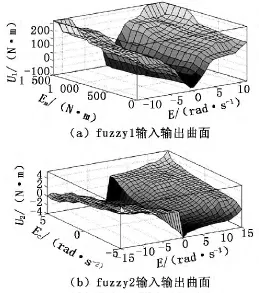
图3 MATLAB仿真模糊控制器输入输出曲面
[1]杨得军,林柏忠,郭学立,等.汽车动力传动系实时动力学仿真模型[J].汽车工程,2006,28(5):430-432.
[2]王建华,王云成,付铁军,等.装用机械摩擦片式限滑差速器后轮驱动车辆的动力性[J].吉林大学学报(工学版),2006,32(2):161-165.
[3]余志生,夏群生.汽车理论[M].北京:机械工业出版社,2002.
[4]赵明旺.智能控制[M].武汉:华中科技大学出版社,2010.
[5]Will A B,Zak S H.Antilock brake system modeling and fuzzy control[J].Vehicle Design,2000,24:221-233.
