置氢α钛几何与能量的第一性原理研究
2015-12-31魏圣泉郑玉斌王玉洁袁宝国
魏圣泉,郑玉斌,王玉洁,袁宝国
(合肥工业大学材料科学与工程学院,合肥 230009)
钛合金由于其优异的力学性能以及耐高温、抗腐蚀性强等特点,在航空航天领域有着广泛的应用[1—3]。长久以来,氢元素的富集一直被认为是导致钛合金发生氢脆的主要原因;而近年来的研究发现,适当含量的氢,可以改变钛合金的显微组织,从而改善钛合金的加工性能[4]。如1959年西德学者Zwiecker和Schleicher发现,适当含量的氢有利于改善钛合金热压力加工性能;李晓华[5]发现一定含量的氢可以明显减小钛合金的高温变形流变应力,如氢含量为0.3%(质量分数)时,流变应力峰值降低36% ~60%,变形温度降低50℃。
基于密度泛函理论的第一性原理是基于体系的哈密顿量,通过求解多粒子体系的薛定谔方程来研究体系的电子结构[6]。刘林飞[7]等人借助第一原理赝势平面波的方法,计算出了C,N,O在α铁中的扩散激活能,得出的结果与实验的误差小于6.2%;尚家香[8]等人通过第一性原理方法研究了氢原子在B2-NiAl和Cr合金中的占位以及对键合作用的影响,预测H在B2-NiAl/Cr体系中主要占据Cr的四面体间隙位置。
本研究采用第一性原理方法对Ti-H体系的几何结构和电子能量进行计算,研究不同氢含量对Ti-H体系结构和能量变化的影响。
1 计算模型和方法
1.1 计算模型
钛具有2种同素异形体,在882.5℃以下为密排六方结构(hcp)的α钛晶体;882.5℃至熔点间为体心立方结构(bcc)的β钛晶体。考虑到钛的实际应用,只取α钛为研究对象,α钛的理论晶格常数为:a=b=0.295 06 nm,c=0.464 78 nm,α=β=90°,γ =120°,空间群为 P63/MMC。采用超晶胞(Supercell)方法构建了α钛和氢物质的量比分别为16∶1,12∶1,8∶1,6∶1,16∶3 的钛氢结构模型,其中氢原子占据了α钛的八面体间隙位置,对应氢含量(质量分数)分别为 0.13%,0.1733%,0.2597%,0.3460%,0.3891%,理论模型见图1。
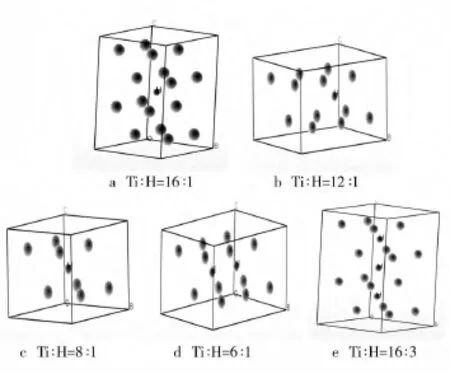
图1 H原子位于八面体间隙的α-Ti-H晶体结构模型Fig.1 Crystal structure models of α-Ti-H with one H atom at octahedral site
1.2 计算方法
所有计算均在基于密度泛函理论(DFT)的第一原理量子力学软件CASTEP(cambridge sequential total energy package)中进行。第一性原理又称从头计算,不需要任何经验参数,只需一些必要的晶体结构参数,通过求解多粒子系统的薛定谔方程来精确获得体系的结构与能量信息。首先通过绝热近似(波恩-奥本海默近似)[9]将电子和原子核运动分离,进而把多粒子体系转化成多电子系统;再利用Hartree-Fock方程与密度泛函近似理论,提出每个电子周围所处的势场可以看成等效势场,体系的能量由电子密度值唯一确定,这样就将多电子体系转化成了单电子体系;在上述近似的基础上,Kohn和Sham于1965年提出了一套用于求解多粒子系统能量与结构的Kohn-Sham方程,如式(1)所示。
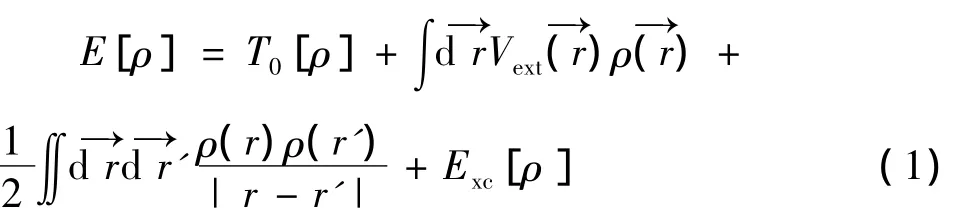
式中:E[ρ]为体系能量,由体系的电子密度确定,公式右侧第1项代表体系的动能,第2项代表电子在相同局域势Vext下受到的外势场影响,第3项是体系电子之间的库伦排斥项,第4项表示电子直接相互作用的交换关联项[10]。Kohn-Sham方程将具有相同粒子数密度且无相互作用的粒子动能T0[ρ]替代T[ρ],把T[ρ]和T0[ρ]两者之间的误差部分转移到交换关联项Exc[ρ]中。1965年W.Kohn和L.J.Sham提出用均匀电子气的交换关联能密度来代替非均匀的交换关联能密度,即所谓的局域密度近似(LDA):Exc[ρ]=∫εxc[ρ(r)]ρ(r)dr,该近似得到的模拟结果与实验值高度吻合,在计算科学领域得到了广泛的应用[11]。1986年,J.P.Perdew和K.Burke在LDA近似的基础上提出了广义梯度近似(GGA)[12],即交换关联项不仅与空间一点的局域密度(LDA)相关,还与电子附近的密度相关,即关联于电子的密度梯度,GGA近似的表示方程如下:,实际应用中经常采用的交换关联势有PW91,PBE,Beeke,RPBE等。
基于上述理论基础,采用周期性边界条件,用平面波基组展开多电子体系,Kohn-Sham方程中的外部势Vext采用超软赝势(USP)表示,交换关联能运用GGA下的PW91泛函近似,平面波截止能量精度设为Precise并调高Ecut为360 eV,布里渊区K点取值精度为Fine级别(3×5×5)。采用BFGS算法对电子体系进行几何优化,收敛条件设置如下:原子总能量收敛值为5.0×10-6eV/atom,原子的最大位移偏差值为5.0×10-4nm,原子的最大受力值小于0.01 eV/atom,最大应力值小于0.02 GPa。
2 计算结果与讨论
2.1 置氢对晶体结构的影响
将不同氢含量的α钛超晶胞完全弛豫,稳态后的晶格参数如表1所示。图2是不同氢含量时α Ti-H的体积、体积膨胀率变化情况。在Ti晶格的八面体间隙位置引入的H原子使Ti晶格发生畸变,随着氢含量的增加,晶胞的平衡常数a,b,c均有一定程度的增大,同时置氢后α钛的体积与体积膨胀率变大,说明置氢加速了α Ti-H的晶格畸变。如置氢量为 0.3891%时,α钛的膨胀率最大,达到1.8687%。比较不同氢含量α Ti-H的晶体结构可以发现,在低氢浓度(Ti∶H=12∶1)时晶胞保持密排六方(hcp)结构,较高氢浓度时变为稍微扭曲的密排六方结构,体积膨胀导致畸变能增大,当氢浓度达到一定的限度时,晶胞结构不稳定,容易生成更为稳定的Ti-H化合物[13]。
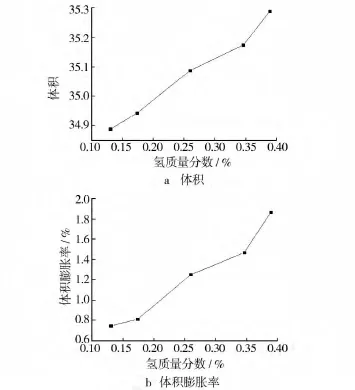
图2 氢含量对α-钛体积及体积膨胀率的影响Fig.2 Effect of the hydrogen content on the volume(a)and on the volume expansion rate(b)of α-titanium crystal

表1 α钛晶体的晶格常数计算结果Table 1 Calculated results of lattice constants of α-Ti
2.2 杂质形成能
为了讨论不同浓度的氢原子在α钛晶胞中的占位稳定性,分别计算了氢在Ti中的杂质形成能,杂质形成能采用式(2)计算。
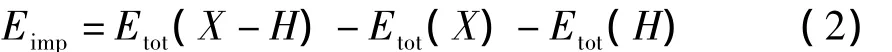
式中:Eimp为杂质形成能,X表示Ti,H表示氢原子,Etot(X-H)表示包含氢原子在内的α钛体系总能量,Etot(X)表示纯Ti体系总能量,Etot(H)表示一个氢原子的总能量[14]。经计算,自由Ti原子和H原子的能量分别为-1601.012 eV和-13.310 eV,钛氢物质的量比为16∶1的晶胞达到稳定后的能量为-25 679.094 9 eV,考虑到其超晶胞建模为(2×2×2)方式,换算成单晶胞得到的稳态能量为-3 209.886 9 eV,利用相同方法计算不同氢浓度下Ti-H晶胞的稳态能量与杂质形成能,结果如表2所示。

表2 α钛晶体的能量与杂质形成能计算结果Table 2 Calculated results of energy and Eimpof α-Ti
由表2可知,随着氢浓度的增加,Ti-H体系的稳态能量呈逐步下降趋势,同时杂质形成能Eimp也随着氢含量的增大而减小,从稳态能量和杂质形成能两方面可以得出结论:高氢含量的α-Ti晶体稳定性高于低氢含量的α-Ti晶体。
3 结论
1)置氢后α钛晶胞发生晶格畸变,导致Ti-H晶体发生体积膨胀,且体积膨胀率随着氢原子浓度的增加而增大,低氢浓度时晶胞保持hcp结构,高浓度时为稍微变形的hcp结构,因晶格畸变而储存的能量会促进Ti-H化合物的生成。
2)随着氢含量的增加,Ti-H晶体的能量和杂质形成能均呈下降趋势,α钛的稳定性进一步增强。
[1]姜波,王耀奇,侯红亮,等.氢对TC21合金高温变形行为的影响[J].材料工程,2011(5):70—75.
JIANG Bo,WANG Yao-qi,HOU Hong-liang,et al.Effects of Hydrogen on Hot Deformation Behavior of TC21 Alloys[J].Journal of Materials Engineering,2011(5):70—75.
[2]戴俊,李鑫,鲁世强,等.TC21钛合金高温变形本构方程研究[J].精密成形工程,2014,6(6):116—121.
DAI Jun,LI Xin,LU Shi-qiang,et al.Constitutive Equation of Titanium Alloy TC21 Deformation at High Temperature[J].Journal of Netshape Forming Engineering,2014,6(6):116—121.
[3]詹梅,褚强,石丰,等.TA15钛合金板材不贴模加热旋压成形规律研究[J].精密成形工程,2014,6(5):31—36.
ZHAN Mei,CHU Qiang,SHI Feng,et al.Forming Law of Flexible Hot Spinning of TA15 Titanium alloy[J].Journal of Netshape Forming Engineering,2014,6(5):31—36.
[4]KERR W R.The Effect of Hydrogen as a Temporary Alloying Element on the Microstructure and Tensile Properties of Ti-6Al-4V[J].Metallurgical Transactions A,1985,16(6):1077—1087.
[5]李晓华,牛勇,侯红亮,等.置氢Ti-6Al-4V合金显微组织演变与高温变形行为[J].中国有色金属学报,2008,18(8):1414—1420.
LI Xiao-hua,NIU Yong,HOU Hong-liang,et al.Microstructure Evolution and High Temperature Deforming Behavior of Hydrogenated Ti-6Al-4V alloy[J].The Chinese Journal of Nonferrous Metals,2008,18(8):1414—1420.
[6]王爱军.Ti-Al(Zr,Hf)-N耐磨涂层的热力学及力学性质的第一原理计算[D].长沙:中南大学,2012.
WANG Ai-jun.First-principles Calculations on the Thermodynamic and Mechanical Properties of Ti-Al-(Zr,Hf)-N Wear-resistant Coating Systems[D].Changsha:Central South University,2012.
[7]刘林飞,周上祺,黄玉堂,等.C,N,O在α-Fe中扩散激活能的计算[J].材料导报,2008,22(8):120—122.
LIU Lin-fei,ZHOU Shang-qi,HUANG Yu-tang,et al.Computation of Diffusion Activation Energies of C,N and O in α-Fe[J].Materials Review,2008,22(8):120—122.
[8]尚家香,于潭波.NiAl和Cr材料中H原子间隙的第一性原理计算[J].物理学报,2009,58(2):1179—1184.
SHANG Jia-xiang,YU Tan-bo.First-principles Study of Hydrogen Atom in Interstitial Sites of NiAl and Cr[J].Acta Physica Sinica,2009,58(2):1179—1184.
[9]BORN M,OPPENHEIMER R.Zur Quantentheorie der Molekeln[J].Annalen Der Physik,1927(20):457—484.
[10]KOHN W,SHAM L J.Self-Consistent Equations Including Exchange and Correlation Effects[J].Physical Review,1965,140(4A):1133—1138.
[11]PERDEW J P,ZUNGER A.Self-interaction Correction to Density-functional Approximations for Many-electron Systems[J].Physical Review B,1981,23(10):5048—5079.
[12]PERDEW J P,BURKE K,ERNZERHOF M.Generalized Gradient Approximation Made Simple[J].Physical Review Letters,1996,77(18):3865—3868.
[13]韩秀丽,王清,孙东立,等.钛-氢体系晶体结构和能量的第一原理计算[J].中国有色金属学报,2008,18(3):523—528.
HAN Xiu-li,WANG Qing,SUN Dong-li,et al.First-principles Calculation of Crystal Structures and Energies of Ti-H System[J].The Chinese Journal of Nonferrous Metals,2008,18(3):523—528.
[14]WEI Y,ZHANG Y,LU G,et al.A first-principles Study of Site Occupancy and Interfacial Energetics of an H-doped TiAl-Ti3Al Alloy[J].Science China Physics,Mechanics and Astronomy,2012,55(2):228—234.
