一种基于椭圆曲线的前向安全数字签名
2015-12-31陈辉焱万宗杰
陈辉焱 ,袁 勇 ,万宗杰 ,刘 乐 ,杨 毅
(1.北京电子科技学院 北京100070;2.西安电子科技大学 西安 710071)
1 引言
在一般的数字签名中,签名密钥一旦泄露,不但后面签名的安全性无法保证,先前签名的安全性也无法保证。为了解决这个问题,几种不同的方式被提出。很多人尝试通过几个系统的密钥分配来降低密钥泄露的可能性。就像在参考文献[1]中提到的,这种方法十分昂贵,以至于对于个体用户来说并不实用。既然每一个系统仍然可能遭受相同的攻击,因此实际的风险也并没有减少。
另一种降低由于密钥泄露所引起安全性的方法被称为前向安全。主要思想是确保密钥仅在很短的时间段内使用,当前的密钥泄露并不会影响前面时间段的安全性。设计一个如此系统的挑战在于,在不改变公共信息的前提下改变秘密信息。这种方式在参考文献[2,3]中在密钥交换背景下被看作前向安全。在数字签名中,前向安全与一些简单的方案首先被Anderson[4]提出。Bellare和Miner[5]首次给出了前向安全数字签名的正式定义,并基于Fiat A和Shamir A[6]签名方案给出了两个前向安全数字签名方案。
前向安全数字签名的主要思想是在传统的数字签名方案中添加了“密钥进化算法”。在密钥进化算法中,密钥被拆分为很多时间段,在每一个时间段中有不同的密钥。每一个密钥被用于签名特定时间段的签名信息,并且在每一个时间段结束时产生新的密钥。前一时间段的密钥被抹去。就像一般的签名方案一样,在所有的时间段内只存在唯一的公钥。验证算法不仅要检测签名是否有效,而且还要检测它是否是在特定的时间段内产生的。因此在一个具有前向安全的方案中,自适应选择信息的攻击者即使获得了当前时间段的密钥想要伪造前面时间段的签名是困难的。特别是过去的密钥并不能通过当前的密钥获得。在一个前向安全数字签名方案中,即使当前的密钥泄露了,过去时间段的签名仍然是可信的。
目前,多数前向签名方案的安全性都是建立在大素数因子分解和有限域离散对数问题之上的。随着用户对安全性要求的提高,密钥长度势必增加,造成了基于乘法群上的数字签名方案运行速度大大降低,使得现有的前向签名方案无法再适应拥挤的网络、智能卡和无线终端等资源有限的设备和环境,使得前向签名的实用性大大减弱。随着设备的要求越来越苛刻,椭圆曲线密码体制的优越性进一步体现出来。对于具有同样规模的密码参数,椭圆曲线加密(elliptic curve cryptography,ECC)算法每一字节密钥的强度要比RSA和ElGamal密码系统大得多。而要达到相同的加密强度,ECC参数的规模要比上述两者小得多。这使得ECC和椭圆曲线数字签名算法 (elliptic curve digital signature algorithm,ECDSA)在实现和实际应用中具有更快的速度和更大的安全优势[7]。
随着近两年计算机网络以及移动通信终端技术的快速发展,椭圆曲线密码体制[8]越来越受到人们的重视,正逐步成为当前主流的公钥密码体制。参考文献[9]提出了一种基于椭圆曲线的前向数字签名方案,但是该方案并不具备真正的前向安全性。因为攻击者一旦知道了签名人任意时段的签名私钥就可以伪造签名者任意时段的签名。因此本文在研究A-R算法[10]的基础上,根据椭圆曲线的相关知识构建了一种全新的基于椭圆曲线的前向安全数字签名方案。该方案具有真正的前向安全性,在下文将会进行详细的论述。
2 基本概念
本文用到的符号说明如下。
·Fp:表示有p个元素的有限域,其特征为大素数p。
·Zn*:表示有n个元素的整数环Zn除了0元素以外的其他所有元素。
·h(m):表示信息m用散列函数进行处理后的输出值。
2.1 前向安全签名方案的定义及性质
前向安全签名的定义如下。
定义1 (前向安全数字签名方案)前向安全数字签名方案一般包括密钥生成算法、密钥进化算法、签名算法和验证算法。可以形式化地表示为FS=(KG,evolving,sign,verify)。下面分别介绍这4个算法。
· 密钥生成(key generator,KG)算法:在该算法中,选择k∈N,T表示方案运行的总周期数,把作为秘密参数的k、T和其他参数输入系统,输出公钥PK和初始私钥SK0。用(PK,SK0)←KG(1k,T)表示。
· 密钥进化(evolving)算法:在该算法中,用户在本周期(j-1)结束时输入当前周期的私钥SKj-1,输出下一周期私钥SKj,然后删除上一周期的私钥SKj-1。用SKj←Evo(SKj-1)表 示 。
· 签名(sign)算法:在该算法中,输入已知的当前周期j、私钥SKj和要签名的签名消息M;输出该周期对消息M的签名(j,ξ)。用(j,ξ)←SgnSKj(M)表示。
·验证(verify)算法:在该算法中,输入已知的当前周期j、公钥PK、签名消息M、待验证签名(j,ξ);输出值为0表示拒绝该签名,输出值为1表示接受该签名。用b←VfPK(M,(j,ξ))表示。
在上面4个算法中,密钥产生算法和签名算法为概率性算法;而密钥进化算法和验证算法为确定性算法。约定如果总周期数为T,则SKT+1为空字符串。
定义 2 (不可伪造性)不可伪造性(unforgeability)是指在不知道前向安全签名私钥的条件下,任何攻击者都不可能成功伪造任何一个有效的前向安全签名。
定义3 (前向安全性)前向安全性(forward-secure)是指在前向签名方案中,即使入侵者获得了在t时刻的密钥,也无法还原t时刻之前的密钥,从而无法伪造t时刻之前的签名。
2.2 基于的困难问题
定义4 (椭圆曲线离散对数问题)给定一个椭圆曲线曲线E,P为椭圆曲线上的一点,且阶为大素数n。选取一随机数k∈,可以很容易计算出Q=kP。但是如果知道P和Q,求解k却是十分困难的。
定义5 (大数分解问题)p和q为两个大素数,N=p·q。知道p和q求解N是容易的,但是如果知道N想要求出p和q却变得十分困难。
3 基于椭圆曲线的前向安全签名设计
(1)密钥生成算法
·选取一条在域FP上的安全椭圆曲线E,取属于E上的一点P,其阶为大素数n。
· 设方案的总周期为T。随机选取两个不同的大素数p1和p2,计算N=p1p2且N>n。
· 取整数d0∈,输出私钥SK0=d0。
(2)密钥进化算法

(3)签名算法
①取整数k,使k∈。
②计算k2T+1-jP=(x,y),r=xmodn。若r=0,则转到步骤①。
③计算消息的散列值e=h(m||r||j),s=SKjekmodn。若s=0,则转到步骤①。
④发送签名(j,ξ)和信息m给验证者,其中ξ=(r,s)。
(4)验证算法
· 取得公钥PK=(P,E,n,Q),签名(j,ξ)和信息m,验证r,s∈。
· 计算e=h(m||r||j)。
· 计算(se-1)2T+1-jQ=(x1,y1)。
· 计算v=x1modn。
· 计算v=r,若成立,签名有效;否则签名无效。
4 安全性分析
4.1 正确性
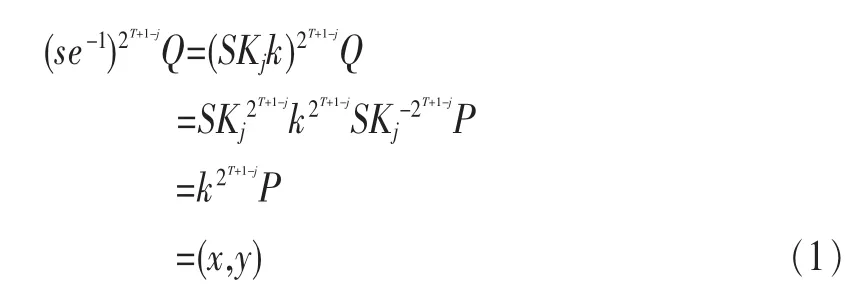
所以本方案显然是正确的。
4.2 前向安全性
(1)密钥进化算法的前向安全性

(2)签名算法的前向安全性
假如攻击者已经获得了第j时段的私钥,它如果想要第j时段的私钥来伪造第j-1时段的签名,如式(2):
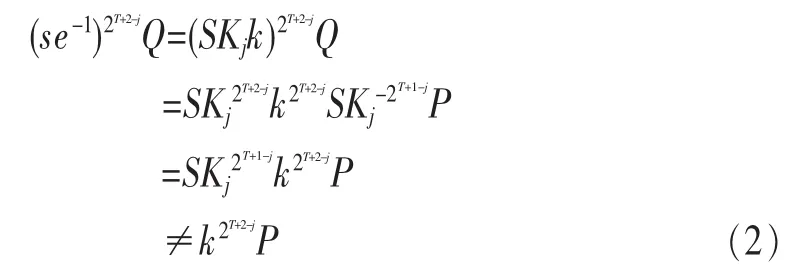
通过上面的分析,本方案解决了攻击者一旦知道了签名人任意时段的签名私钥,在不知道前面时刻私钥的情况下就可以伪造签名者任意时段签名的问题。
因此,通过以上两部分的系统分析可以得出:当攻击者知道第j时段的签名以及私钥时,攻击者无法伪造j时段之前的签名。所以本签名方案具有真正意义上的前向安全性。
4.3 抗伪造性
PK作为签名算法的公钥,如果攻击者想通过公钥PK中的参数Q来获取私钥SKj,那么他将面临椭圆曲线的离散对数问题。因此攻击者是无法通过公钥来获取签名者的私钥SKj。签名s作为签名在j时段的签名重要组成部分,由s=SKjekmodn可知,如果攻击者想通过s得到实际签名私钥SKj就必须知道k的值。而如果想要求解k就要面临椭圆曲线离散对数的求解问题,因此攻击者无法通过s获得签名私钥SKj。由前面的验证算法可知,如果攻击者在不知道私钥SKj和k的情况下,想用一个伪造的私钥进行签名,则验证无法通过,具体证明过程如下。
假设攻击者伪造j时段的私钥′,随机选取随机数计算 s′=SKj′ek′mod n,k′2T+1-jP=(x′,y′) 和 r′=x′mod n,进而伪造 j时段的签名记为(j,ξ′),其中 ξ′=(r′,s′),但是在验证过程中,由于:

因此,验证无法通过,本方案具有较强的抗伪造性。
5 方案性能
通过对基于椭圆曲线的前向安全数字签名方案的4个算法的描述能够发现:在密钥进化算法中采用的是二次剩余运算;在签名算法中只进行了一次点乘运算和零次模逆运算;在验证算法中只进行了一次点乘运算和一次模逆运算。在基于椭圆曲线的数字签名算法中最耗费时间的就是点乘运算和模逆运算,因此,本方案的签名与验证速度是非常快速的,计算效率也是相当可观的。
6 结束语
椭圆曲线密码已成为当前的主流密码算法,在人们的日常生活中发挥着越来越大的作用。本文基于椭圆曲线的离散对数问题构造了一种基于椭圆曲线的高效前向安全数字签名方案,并有力地保证了新签名方案的正确性和安全性,在电子商务或电子政务等领域中,具有广泛的应用前景。
1 Bellare M,Rogaway P.The exact security of digital signatures:how to sign with RSA and Rabin.Proceedings of Cryptology-Eucocrypt 1996 Lecture Notes in Computer Science(LNCS),Cambridge,UK,1996:399~416
2 Guillou L,Quisquater J.A practical zero-knowledge protocol fitted to security microprocessor minimizing both transmission and memory.Proceedings of Cryptology-Eurocrypt 1988 Lecture Notes in Computer Science(LNCS),Davos,Switzerland,1988
3 Micali S.Asecure and Efficient Digital Signature Algorithm.Technical Report,MIT/LCS/TM-501,1994
4 Anderson R.Two remarks on public-key cryptology.Proceedings of the 4th Annual Computer and Communications Security(ACM),Zurich,Switzerland,1997
5 Bellare M,MinerS K.A forward-secure digitalsignature scheme.Proceedings of the 19th Annual International Cryptology Conference,Santa Barbara,CAL,USA,1999:431~448
6 Fiat A,Shamir A.How to prove yourself:practical solutions to identification and signature problems. Proceedings of Cryptology-Crypto’86,Santa Barbara,CAL,USA,1986:186~194
7 隋爱芬,杨义先,钮心忻等.基于椭圆曲线密码的可认证密钥协商协议的研究.北京邮电大学学报,2004,27(3):28~32
Sui A F,Yang Y X,Niu X X,et al.Research on the authenticated key agreement protocol based on elliptic curve cryptography.JournalofBeijing University ofPosts and Telecommunications,2004,27(3):28~32
8 蔡满春,杨义先,胡正明.基于椭圆曲线密码机制的一种电子现金方案.北京邮电大学学报,2004,27(2):44~47
Cai M C,Yang Y X,Hu Z M.Electronic cash scheme based on elliptic curve cryptosystem.Journal of Beijing University of Posts and Telecommunications,2004,27(2):44~47
9 王尚平,候红霞,李敏.基于椭圆曲线的前向安全数字签名方案.计算机工程与应用,2006(18):150~151
Wang S P,Hou H X,Li M.A forward-secure digital signature scheme based on elliptic curves.Computer Engineering and Applications,2006(18):150~151
10 Michel A,Leonid R.A new forward-secure digital signature scheme.Proceedings of Advances in Cryptology-Asiacrypt 2000,Kyoto,Japan,2000:116~129
