云计算中一种高效的虚拟机在线动态分配算法
2015-12-31张丽敏
张丽敏
(西安外事学院现代教育技术中心 西安 710077)
1 引言
虚拟技术为云供应商提供更加便捷的方法来分配计算资源。云供应商定义不同的虚拟机(VM)组合,并以VM实例为单位出售资源。当前,云供应商使用定价策略分配和出售VM实例[1],使用拍卖算法来出售定价之后仍然闲置的资源。云供应商希望分配算法能够支持动态供应,以便他们根据市场需求就不同类型的VM实例数量做出决策。云供应商也希望实现营运收入最大化。
多篇文献已经对云计算的经济问题进行了研究。参考文献[2]针对目前国内并没有相应的云计算计价标准,价格高低直接影响网络利用率和收益的问题,在计价时考虑价格因素对网络负载的影响,提出了一种改进的蚁群算法,解决了计算资源闲置导致的网络利用率低下和收益减少问题。参考文献[3]提出了一种面向资源分配的第k+1个价格拍卖算法。通过理论分析与仿真得出,当资源和用户较多时,该算法既可以提高分配的效率,又可以增加云服务商的收入。参考文献[4]设计了一种基于马尔可夫决策过程的资源在线算法,给出了同一模型面对大规模问题时的近似求解方法。参考文献[5]设计了一种并行系统下可拓展并行作业的资源在线调度算法。该算法在其模型中支持作业抢占,如果作业的价值更高,那么即使提交时间晚于当前分配的作业,也可以获得优先权支持。参考文献[6]提出了一种云资源调度模型(cloud-resource scheduling model,CSM),该模型以实现效用最大为调度目标,可以充分提高用户的满意程度。文中通过求解CSM优化问题得到最优的虚拟机和物理机映射关系,实现了对云资源的最优分配。
另外,参考文献[7]针对云商务环境下信息服务资源分配过程中的定价问题,分别建立了服务者、服务用户和服务环境的模型,并提出相应的求解方法。仿真实验结果表明,当交易者的规模增加时,该方法可以在保证第三方收入的情况下,使参与交易的双方获取更高的服务效用。参考文献[8]提出了一种基于组合拍卖的VM分配算法CA-Provision,该算法通过假设资源以数量固定但类型不同的VM实例形式提前供应,从而解决VM分配问题。另外,CA-Provision算法拓展了参考文献[7]中的模型,并支持VM实例的动态供应和分配。然而,该算法在运行时需要收集一段时间内所有用户请求的所有信息,即这些算法是离线算法,需要定期运行来为用户分配资源。
为此,本文设计了一种云条件下VM实例的在线供应和分配算法。首先,设计了一种申请协议,当用户申请一批VM时,表明用户只对整批VM感兴趣,而不是其中的一部分。在接收到这些申请后,本文算法在线计算分配策略和花费。同时,分配不得被抢占,如果用户在时间t接收到分配策略,则在用户所请求的该段时间内始终占有资源。最后,通过理论分析和仿真实验验证了本文算法的有效性。
2 VM实例分配问题
假设云服务提供商提供的计算资源共有m种不同的VM实例类型,本文将这些实例类型表示为VM1,…,VMm。对每种类型的实例 VMi关联一个 “权重”ωi∈,ωi表示VMi相对云供应商提供的最强大VM实例 (即类型为VM1的实例)的计算能力。不失一般性,本文认为ω1=1且ω1≤…≤ωm。将可以用于分配的可用计算资源的总计算能力表示为M,定义为类型VM1的M个实例的等价计算能力。假设云供应商提供3种类型的VM实例:小型(VM1)、中型(VM2)、大型(VM3)。这些 VM 的配置如下:VM1为 1 个2 GHz处理器、8 GB内存、2 TB硬盘;VM2为 2个 2 GHz处理器、8 GB内存、2 TB硬盘;VM3为2个2 GHz处理器、16 GB内存、4 TB硬盘。对于该配置来说,VM的权重为:ω1=1、ω2=2、ω3=4。假设云提供商有足够的资源来提供100 000个VM1实例,则M=100 000。云提供商的目的是将其可用资源动态供应为VM实例,在将其高效提供给用户的同时实现收益最大化。
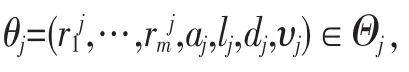


满足的约束条件为:

式(1)表示问题的目标,即云供应商使成功申请资源的用户价值之和最大化。式( 2 ) 表示在已知时间t分配的资源不得超过最大可用资源数量M。其中,,该集合表示在时间t及t之前分配到资源,并且在时间t所分配到的时间间隙还没有结束的用户集合。
上述问题的一种直接求解方法就是选择价值最大的用户,然后向这些用户收取各自的费用。然而,用户是理性用户,他们可能为了自身利益而误报自己的类型。例如,用户可能少报价值以便减少支付额度,或者多报价值以增加被分配概率。如果云提供商偏好截止日期较早的作业而忽略价值,则用户可能会早报他们的截止日期。因为这一信息是隐私信息,所以提供商需要使用一种算法来根据用户报告的价值计算分配策略及相关费用,以便提供商设定的全系统目标能够实现。
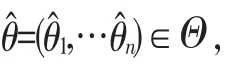
3 在线算法的设计

每个用户j可将价值函数Vj定义如下:

如果用户申请成功,则用户接收到的价值为υj;否则,接收到的价值为0。本文用效用函数来定量描述用户j的效益,该效用函数定义为用户从算法接收到的价值与用户需要支付的费用之差,即:

如果在线算法拒绝为其分配资源,则用户接收到的价值为0。此时,如果算法不向其收取任何费用,用户的效用也将为0。
定义 1 (激励作用)如果对任意用户j有∈Θj、-j∈Θ-j、并满足式(5),则算法E具有激励作用[9]。

用户如果不管其他用户的申请如何,而把自己的真实类型汇报给算法,则可以实现自身效用最大化。这是非常重要的算法,因为如果满足这一属性,参与算法的用户就不会向算法汇报虚假类型,即汇报真实属性是用户的最优策略。


不管其他用户的申请如何,用户只要参与在线算法并汇报了自己的真实类型,自己的效用一定不会为负。这也是在线算法的重要属性,因为可以鼓励用户积极参与在线算法。为了使算法具有激励作用,分配函数A必须单调且费用函数P必须实现临界值支付[10]。


如果用户j通过汇报类型而申请成功,则该用户汇报也会申请成功 ,其 中′比更 受 偏 好 。
定义4 (临界值支付)用户j的临界值 定义为

临界值是指用户为了申请成功而必须向算法汇报的最小值。费用函数应该向用户收取临界值费用,以便使算法具有激励功能。本文设计了一种解决OVMPA问题的在线算法。
4 在线VM分配算法
本节给出了解决OVMPA问题的在线VM分配和供应算法。
4.1 ODAA-VM
ODAA-VM采取事件处理程序架构,当新的申请到达或者用户分配到的批量资源到期,并且将VM实例返回给供应商时,调用事件处理程序。假设通过某种标准化协议,用户和资源的信息对算法是已知的。ODAA-VM利用这一信息来确定用户集合及当前时间可用资源,并可调用分配函数和费用函数。ODAA-VM流程如下。


ODAA-VM以事件、当前分配集合及费用集合为输入。事件类型包括资源的释放或到达的用户申请。假设系统存储这两个集合,并且当ODAA-VM被调用时将其传输给ODAA-VM。ODAA-VM更新集合,然后返回给系统。在第1~4行,ODAA-VM设置当前时间为t,且3个变量的初始化如下:N(t)为迄今还没有申请成功的用户申请集合;(t)为已经成功申请但是分配的资源还没有到期的用户申请集合;M(t)为在时间t可用于分配的资源总权重。只有当资源和用户可用时,算法才会运行。算法会调用以未获得成功的用户申请和时间可用资源为参数的函数ODAA-VM-Allocate。ODAA-VM-Allocate函数(见第4.2节)返回在时间t申请成功的用户集合A(t)。
然后,ODAA-VM将整个分配集合A更新为A(t)。A(t)中的申请也被插入费用集合,且 为初始费用。然而,通过调用ODAA-VM-Payment函数(见第4.3节)可以更新该费用(第11行)。实际上,用户j的费用会被更新多次,直到t=δj(即用户接收到所要求的批量实例)为止。因此,ODAA-VM-Payment函数计算这些用户的费用并更新费用集合P。ODAA-VM算法的下一个步骤是确定当前时间已经超过δj的用户j的申请集合NP(第12行)。然而,这一集合只包括t′之后已经度过δi时间的用户,其中t′表示上次调用ODAA-VM的时间(第12行)。如果用户j已经分配到了批量资源,则该用户的费用不会再改变,当前时刻的费用即最终费用。如果用户j直到时间t还没有申请成功且t>δj,则用户不会申请到完成他的作业所需要的资源。此时,用户j将支付的费用为pj=0(第14~19行)。
4.2 ODAA-VM-Allocate函数
函数ODAA-VM-Allocate的具体过程如下。



首先,ODAA-VM-Allocate函数按照ρj的非升次序对所有申请排序。按照如下次序打破关联:偏爱更早的δj、更小的以及更小的。然后,当资源允许时,算法将为这些用户分配各自请求的资源。最后,算法返回在时间t被选择分配资源的用户集合A(t)。
ODAA-VM-Allocate函数的目的是实现申请成功的用户价值之和最大化。当存在关联情况时,通过向δj较小的用户赋予优先级(即没有申请成功而将较早离开系统的用户),也可以保证受到服务的用户数量最大化。基于同样原因,对于δj关联情况,资源使用时间较短的用户也将受到优先对待。
4.3 ODAA-VM-Payment函数
ODAA-VM-Payment函数如下。


ODAA-VM-Payment函数的输入包括当前时间t、费用集合P、调用分配函数M(t)之前的可用资源、分配函数N(t)考虑的用户集合以及当前时间t占据资源的用户集合(t)。在时间t申请成功的用户也属于集合N(t)。
ODAA-VM-Payment函数的主要思路是将用户的到达时间看成t,然后计算δj≤t的用户j的临界费用。通过每个事件重复调用这一函数,ODAA-VM可以保证和 δj之间每次出现事件时,均会计算用户j的临界费用。ODAA-VM-Payment函数对 δj≥t的所有用户j计算时间t时的临界值为:
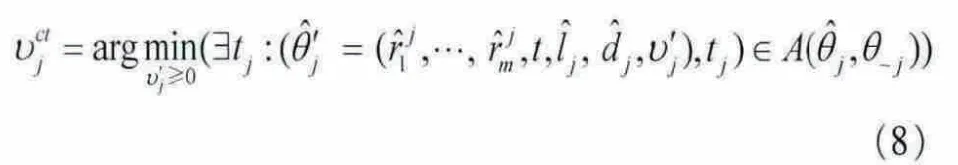
以该临界值为基础,ODAA-VM将临界值计算为:

ODAA-VM-Payment函数考虑费用集合中 δj≤t的用户。对于每个用户j,将其类型的到达时间元素设为t,价值设为每个用户的价值,以便确定用户j为了申请成功而需汇报的最小值(第2~16行)。如果未找到最小值,则将支付费用设为0(第17~21行),也可以将该数值设为预先确定的底价。最后,将更新过的集合P返回给在线算法。在线算法通过调用ODAA-VM-Payment函数以持续更新P,并在时间t向的δj 定理1ODAA-VM具有激励作用。 定理2ODAA-VM的时间复杂度为O(nlogn)。 ODAA-VM主要包括ODAA-VM-Allocate函数和ODAA-VM-Payment函数。其中,ODAA-VM-Allocate函数成本最大的操作是第2行的用户排序,这一操作的复杂度为O(nlogn)。ODAA-VM-Payment函数看上去非常复杂,因为它重复调用ODAA-VM-Allocate函数。但是,在实际部署中,当确定临界值时并不需要调用ODAA-VM-Allocate函数。对申请成功的用户j,需要以他们的非升次序考虑在时间t没有申请成功的用户j′,并且弄清如果j没有参与,用户j′能否申请成功。只需比较j占据的资源和j′请求的资源,就可以弄清这一点。当首次发现这一用户j′时,用户j的费用为′。需要在算法开始时对失败的申请进行一次排序,这一过程的复杂度仍然为O(nlogn)。因此,ODAA-VM的时间复杂度为O(nlogn)。 定理3 ODAA-VM的竞争比为η。 设有两个申请 θ1和 θ2,且s1=1,s2=M,(a1,l1,d1,υ1)=(0,l,l,υ),(a2,l2,d2,υ2)=(1,l,l+1,Mv+ε),l>1。一方面,ODAA-VM 将为用户1分配其在时间l>1要释放的资源。因为对于θ2,有a2+l2=1+l=d2,所以用户2必须在时间a2=1申请成功,否则用户2需要收回申请。由于其无法在截止日期前完成作业,因此ODAA-VM只会为用户1分配VM实例,并获得价值υ(式(1))。另一方面,最优离线算法将为用户2分配资源,获得价值Mυ+ε>M×υ。因此,ODAA-VM 算法的竞争比为 η。 通过对ODAA-VM和一种高性能离线算法的比较,证明ODAA-VM的优缺点。 [8]中的CA-Provision离线算法与本文的ODAA-VM进行比较。CA-Provision算法解决了云环境下的动态VM供应和分配问题。以固定时间间隔(如1 h)调用CA-Provision算法。当调用时,该算法考虑上次间隔期间收集的所有申请,通过组合拍卖来确定申请成功的用户、费用及分配的VM实例数量。分配的VM实例只能使用一个时间间隔,用户如果需要继续访问资源,就必须继续申请,直到满足这些用户的时间要求。如果需求量上升,则当前分配给用户的资源在以后可能被抢占。 本文使用的输入来自于参考文献[11]中的Parallel Workload Archive(并行工作负载数据库)。表1给出了工作负载的日志信息及相关统计信息,前4列分别为工作负载日志的名称、日志的采集时间、作业数量及日志总小时数,第5列给出了生成日志的系统的处理器数量。假设VM实例的权重对应于分配给该实例的处理器数量,则一个系统的处理器总数量表示计算资源的总权重s,将分配给工作负载ω的总体计算资源表示为Mω。表1的后4列表示相关统计数据:Jω表示每小时递交给系统的平均作业数量;平均运行时间Tω及单个作业的平均处理器数量Pω在计算时考虑工作负载日志的所有记录;最后一列为负载ω的“正规化负载”ηω,其计算式为: 表1 工作负载日志 正规化负载用来衡量请求的平均资源量与可用的单位计算资源之间的相对关系,帮助对异构工作负载进行排序,并解释部分实验结果。 表2 仿真参数 CA-Provision算法根据单个空闲VM实例的相关成本参数计算底价υres=cR-cI。虽然本文没有给出带有底价的ODAA-VM,但是通过抛弃低于底价的用户,并对申请成功的用户收取底价费用而不是0费用(ODAA-VM-Payment函数的第20行),即可集成底价策略。在本文实验中,ODAA-VM的底价与CA-Provision算法的底价相同。表2给出了所有参数值,对每个工作负载日志,基于不同的参数组合进行18次实验。 在图1中总结了每个工作负载的结果。水平轴表示工作负载和正规化负载,垂直轴表示成功申请的用户比例、每个成功申请的用户的平均收入以及每个成功申请的用户的平均效用。在图1(a)中,ODAA-VM的用户服务比例高于CA-Provision算法。最明显的性能增益出现于日志 LLNLuBGL-2006(正规化负载 7.41)和 DAS2-fs0-2003(正规化负载2.01)中,且是这里使用的工作负载的最大值。DAS2-fs0-2003负载的用户服务比例几乎翻倍,LPC-EGEE-2004负载的用户服务比例增长将近6倍。这是因为在CA-Provision算法中,即使有可用资源,用户也必须等待下次拍卖时间。那时,可能有更多用户到达,因此该用户可能拍卖失败。此外,对于部分用户来说,即使在部分拍卖中取得成功,但是如果他们需要长期占用资源来完成任务,将可能发生资源抢占,所以他们会选择离开。由于上述两种工作负载增加了申请密度,所以导致拍卖数量上升,而ODAA-VM由于其在线设计,可以容纳更多的申请。 从图1(b)可知,每个成功申请用户带来的平均收益下降。由于在线算法根据不完全信息确定分配策略,所以无法实现收入最优。一种直观解释就是ODAA-VM通过尽快做出分配决策,帮助用户避免与后续用户竞争。对于CA-Provision算法,用户必须与相同周期内的其他用户展开竞争,因此价格将会上升,但是成功申请用户的数量上升弥补了收益损失。 从图1(c)可以看出,ODAA-VM成功申请用户的平均效用与CA-Provision算法相当。虽然本文希望通过降低用户支出提高用户的效用,但是前提是两次拍卖所选择的分配用户集合相同。这是不可能实现的,原因有两点:一是CA-Provision算法会抢占价值较低的用户,将资源分配给价值高的用户,而ODAA-VM会把VM分配给用户,并让用户在其所申请的整个时段内使用资源,但是如果有价值更高的用户到达,则这可能导致没有可用资源,从而丢失该用户;二是ODAA-VM中成功申请的用户数量要多于CA-Provision算法,这说明ODAA-VM容纳了低价值用户,而这些用户导致平均效用较低。 总体来说,本文认为ODAA-VM提升了用户和云供应商的云体验,云供应商服务了更多用户,增加了用户满意度,最终增加了总体收入。 本文设计了一种云环境下VM在线供应和分配算法。在该算法下,每当有足够多的资源和合适的申请,就会分配VM实例。本文算法对用户具有激励作用,且可在多项式时间内运行;可增加被服务的用户数量,但是降低了平均收益,然而增加的用户数量可以弥补平均收益损失。在未来工作中,将针对CA-Provision算法中用户VM被抢占的情况,设置相应的赔偿代价,并将其再次与ODAA-VM进行比较,观察“用户的平均收益”是否有所改进。 图1 CA-Provision算法和ODAA-VM的总体结果 参考文献 1 刘正伟,文中领,张海涛.云计算和云数据管理技术.计算机研究与发展,2012,49(Z1):26~31 Liu Z W,Wen Z L,Zhang H T.Cloud computing and cloud data management technology.Journal of Computer Research and Development,2012,49(Z1):26~31 2 范杰,彭舰,黎红友.基于蚁群算法的云计算需求弹性算法.计算机应用,2011,31(1):1~4 Fan J,Peng J,Li H Y.Demand elasticity algorithm for cloud computing based on ant colony optimization algorithm.Journal of Computer Applications,2011,31(1):1~4 3 Lin W Y,Lin G Y,Wei H Y.Dynamic auction mechanism for cloud resource allocation.Proceedings of the 10th IEEE/ACM International Conference on Cluster,Cloud and Grid Computing(CCGrid),Melbourne,Australia,2010:591~592 4 ParkesD C,Singh S.An mdp-based approach toonline mechanism design.Proceedings of the 17th Annual Conference on Neural Information Processing Systems,Sydney,Australia,2003:1421~1426 5 Carroll T E,Grosu D.Incentive-compatible online scheduling of malleable parallel jobs with individual deadlines.Proceedings of the 39th International Conference on Parallel Processing,San Diego,CA,USA,2011:418~425 6 师雪霖,徐恪.云虚拟机资源分配的效用最大化模型.计算机学报,2013,36(2):252~262 Shi X L,Xu K.Utility maximization model of virtual machine scheduling in cloud environment.Chinese Journal of Computers,2013,36(2):252~262 7 罗贺,孙锦波,胡笑旋等.云商务环境下的多源信息服务资源分配模型.计算机集成制造系统,2013,19(10):137~142 Luo H,Sun J B,Hu X X,et al.Resource allocation model for multi-sources information service in cloud business.Computer Integrated Manufacturing Systems,2013,19(10):137~142 8 Zaman S,Grosu D.Combinatorial auction-based dynamic vm provisioning and allocation in clouds.Proceedings of IEEE 3rd International Conference on Cloud Computing Technology and Science(CloudCom),Athens,Greece,2011:107~114 9 Zaman S,Grosu D.A combinatorial auction-based mechanism for dynamic VM provisioningand allocation in clouds.IEEE Transactions on Cloud Computing,2013,1(2):129~141 10 Mu’alem A,Nisan N.Truthful approximation mechanisms for restricted combinatorialauctions.Proceedings ofthe 18th National Conference on Artificial Intelligence, Edmonton,Alberta,Canada,2002:379~384 11 Lublin U, Feitelson D G. The workload on parallel supercomputers:modeling the characteristics ofrigid jobs.Journal of Parallel and Distributed Computing,2003,63(11):1105~11225 算法性能

6 实验结果
6.1 实验配置


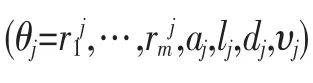

6.2 结果分析
7 结束语

