基于地标的静止轨道遥感卫星测定轨技术研究

罗 达，宋效正，沈毅力，张 洋

（上海卫星工程研究所，上海 200240）

0 引言

传统的卫星测定轨技术基于地面站观测卫星所得的测距、测速和测角信息。处在地球静止轨道（GEO）上的卫星，其相对地面观测站的空间位置变化很小，测速和测角信息不能得到有效利用，通常采用三点测距方法对其进行较高精度的测定轨，其定轨精度可优于100m。因我国布置在境外的地面观测站数量有限，对处于境外地球上空的GEO卫星，一般只能采用单站测定轨的方法进行测定轨，定轨精度在公里以上量级。处理对地遥感静止轨道卫星资料时需将地理经纬度网格精确地标识到卫星获得的地球图像中，因此卫星的轨道确定和预报精度是决定输出图像精确程度的基础，单站测定轨方法的定轨精度已不能满足要求。另外，考虑设备故障或国际形势的变化，地面观测站无法使用等情况，为保障在轨卫星的遥感任务对测定轨精度的要求，需研究无地面观测站条件下的测定轨技术。

地标是具清晰结构特征的地物，包括海岸线、岛屿、河流、湖泊等。有对地遥感功能的飞行器可利用所摄图像中的地标信息，提升自身任务性能。文献［1-2］基于地标信息设计了风云二号气象卫星的图像自动几何精校正方法和极轨气象卫星的自动地标导航方法，提高了图像的定位精度；文献［3］等基于等高地面控制点设计了航空摄像机的参数估计方法，取得了相对误差优于3%的相机参数估计效果；文献［4］基于地标图像信息设计了飞机惯性导航系统误差校正方法；文献［5］设计了根据地标信息进行航天器相对位置保持的算法。本文对基于地标的静止轨道遥感卫星测定轨技术进行了研究。

1 测定轨技术与方案

基于地标信息对遥感卫星进行测定轨原理如图1所示。将地面典型地标库作为模板图像并编号存储于星上计算机中；当卫星所摄地面区域中含地标时，其图像经处理后形成标准图像，与地标模板图像进行匹配，识别出地标及其对应编号；根据地标库中地标的地理坐标数据、地标图像在像平面中的坐标、遥感设备视轴在空间的指向可得地标－像矢量的方位角和俯仰角；根据地面站测距信息可得星－地面站的距离。则由两个角度信息和1个距离信息可确定卫星的空间位置。

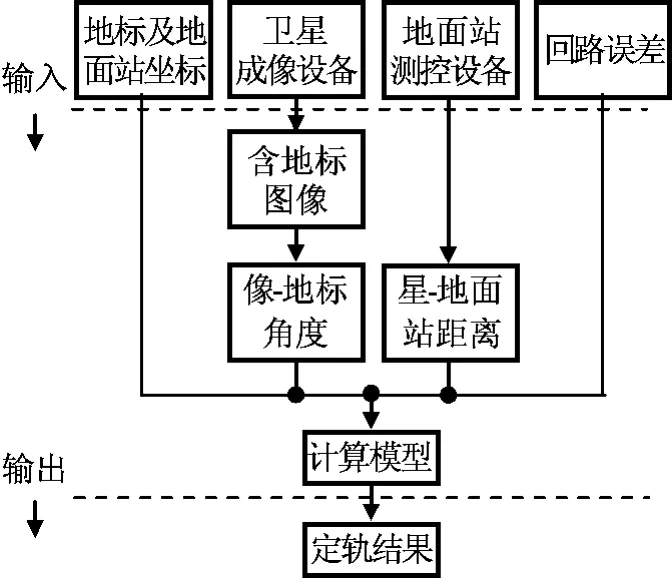
图1 基于地标信息对遥感卫星测定轨原理Fig.1 Principle of orbit determination based on landmark

地标及其所遥感的几何关系如图2所示。在地球固连坐标系Of－XfYfZf中，地标LM的坐标为（XLMf，YLMf，ZLMf），地 面 观 测 站 坐 标 为 （Xsf，Ysf，Zsf），卫星待求位置坐标为（xsatf，ysatf，zsatf）；在像平面坐标系Op－XpYpZp中，地标LM所遥感的坐标为（xLMp，yLMp）。

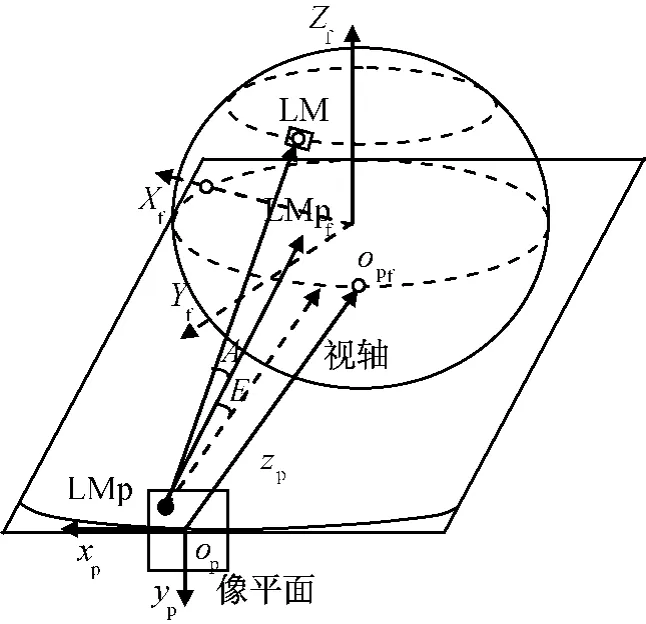
图2 地标及像几何关系模型Fig.2 Geometry model of landmark and image

在地固系中，记相机视轴指向矢量LA＝［xLAyLAzLA］T，可由卫星姿态及卫星与像平面的姿态转换矩阵得到；像元的空间角度分辨率为rp（定值），则地标－像矢量与LA的方位角A和俯仰角E（A，E∈成像视场）可表示为

由此可得像－地标矢量

因像元位置LMp至卫星质心距离相较地标至卫星质心距离很小（＜10－7），故可认为LM即为卫星-地标矢量sat＿LM。

若地面站对卫星的测距结果为Rssat，则卫星在地固系中坐标可表示为

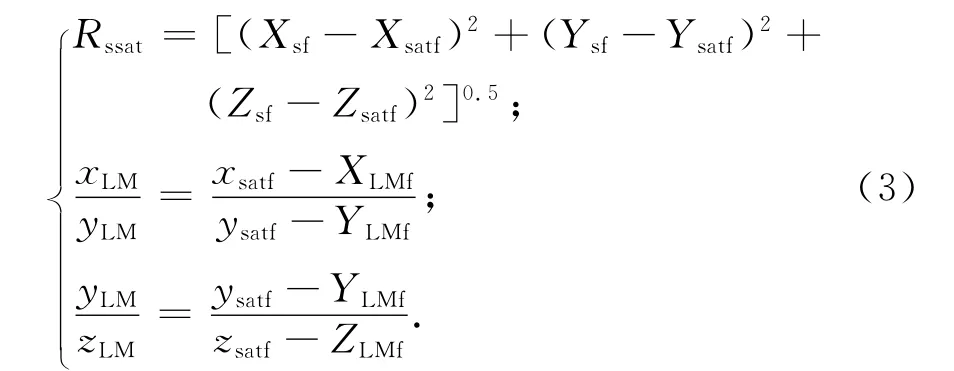
当地面站不可用时，可基于2个或以上地标相对卫星的角度信息，估算卫星的位置：

2 误差项影响

基于地标遥感所得的卫星定轨精度受卫星姿态确定误差、卫星及相机结构变形误差、相机空间分辨率、大气折射和地面站测距误差等的影响。以下分析某误差项时，暂不考虑其他误差的影响。

2.1 卫星姿态确定误差

LA由卫星姿态及卫星与像平面的姿态转换矩阵而得，故卫星姿态确定误差会引入LA，进而通过式（2）、（3）影响sat＿LM，如图3所示。记卫星姿态确定精度为amp，因其量级很小，由其引起的定轨误差可估算为

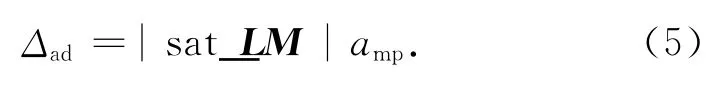
不同卫星姿态确定误差的定轨精度（3σ）见表1。表中：R为地球半径。

图3 姿态测量精度影响Fig.3 Effect of attitude measure precision

表1 不同姿态确定误差下的定轨精度Tab.1 Precision of orbit determination under various satellite attitude estimation

由表1可知：卫星姿态确定精度0.01°～1″时，基于地标定轨误差在千米至100m的量级；定轨误差随卫星与地标距离增大而变大。在当前姿态敏感器测量水平下，可实现3″的姿态确定精度，对应定轨误差约600m。

2.2 结构变形残差

结构变形误差包括卫星及相机由装配、运输、发射等导致的机械变形误差，以及由温度变化导致的热变形误差。该误差项影响了卫星至像平面的姿态转换矩阵、各像元与像平面几何中心的空间关系，需通过标定等进行修正以减小其对卫星遥感任务的影响。不同结构变形残差下的卫星定轨精度（3σ）见表2。

由表2可知：结构变形残差10～100μrad时基于地标定轨误差为100m至千米的量级；定轨误差随卫星与地标距离增大而变大。根据文献，遥感卫星结构变形误差修正后残差约50μrad，对应定轨精度约1.6km［6］。

表2 不同结构变形误差下的定轨精度Tab.2 Precision for orbit determination under various structure deformation

2.3 相机空间分辨率

相机像元的空间分辨能力影响地标遥感在像平面内的坐标偏差大小。对静止轨道上空间分辨率30μrad（3σ）卫星，对应地面的分辨误差约1km，即在地标位置精确已知时，地标的测量位置与真实位置间存在1km的随机差。由平行线性质可推算，其对应卫星的定位误差约1km。

2.4 大气折射大气模型误差

地面特征点反射或自身发出的光线以不同的天顶角通过大气到达卫星相机接收端过程中，会受大气折射和大气湍流等影响而改变光线的波前相位，即对应不同的光线传输方向，最终影响图像定位与配准模型参数的获取精度。

星下点的地面特征点光线方向变化较小，而地球边缘处的地面特征点的光线方向变化相对较大，理论仿真表明不大于2μrad（3σ）。

大气中存在不同强度的湍流，在对空中目标进行测量时目标会发生抖动，从而造成对光线入射角度的测量误差。大气湍流对光线角度的影响如图4所示。由图可知：地面目标受大气湍流影响后，视线角度偏量最大为3μrad（3σ），对光线方向的变化影响较小，其对应卫星的定位误差约100m。

2.5 地面站测距误差

若以地面观测站为圆心，以地面站对卫星的测距值为半径作一球体，sat＿LM与该球体的反向交点即为卫星位置。因此，地面站测距误差导致的定轨误差即为该测距误差值。我国地面站测距误差可控制在10m（3σ）以内。

图4 大气湍流对视线角度偏量影响Fig.4 Effect of atmospheric turbulence for line of sight angle error

3 仿真分析

若在同一幅图像中存在1个地标，可基于其角度信息和地面站测距信息解算卫星位置。若无地面站测量信息，可通过同一幅图像中2个或以上地标计算得到的sat＿LM角度信息，直接解算出卫星位置。若地面站个数为2个，则可利用两站的测距信息，从而提高最终定轨精度。

以东经－40°上空静止卫星为例，地面站1——智利站（东经289.3°、北纬－33.2°，高度733.3m）；地面站2——瑞典站（东经339.0°、北纬67.9°，高度402.3m）；海岸地标1（东经－35.74°、北纬－5.5°）；海岸地标2（东经－81.1°、北纬－4.2°）对其进行测定轨，统计仿真数据1 000组，结果见表3。

为比较其与星上轨道递推误差的差异，取对轨道递推影响最大的径向（R向）定位误差100m，切向T和法向N定位误差为0m，无其他定轨数据支持下自主递推，10d，6月的位置误差分别如图5、6所示。

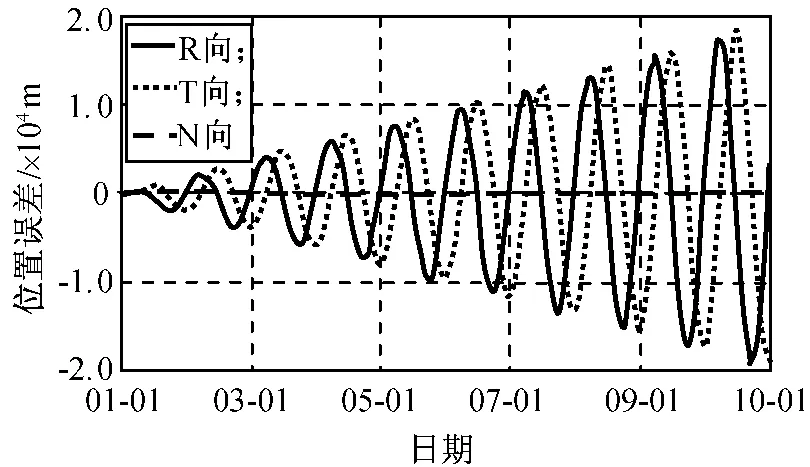
图5 仿真10dR、T、N向位置误差Fig.5 R，T，N position error by simulating 10days

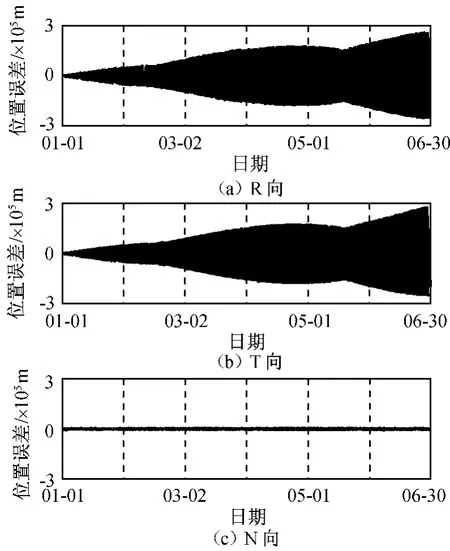
图6 仿真6月R、T、N位置误差Fig.6 R，T，N position error by simulating 6months

表3 不同地标／地面站组合的定轨精度（3σ）Tab.3 The orbit determination precision by different LM and ground stations’combination

由上述仿真结果可知：采用地标的测定轨精度优于星上自主轨道递推10d的定位精度。

4 结束语

本文对基于地标的静止轨道遥感卫星测定轨技术进行了研究。分析了地标遥感回路中各要素对测定轨精度的影响及量级，给出了多种模式的测定轨精度。仿真表明：当地面观测站数量有限或无法工作时，遥感卫星利用所摄图像中的地标信息，可有效确定自身的轨道位置。在现有卫星平台及相机性能条件下，可实现约400m的定轨精度，并且其自主定轨性能不随时间而降低，定轨精度优于星上自主轨道递推多天的定位精度，可实现数天至数月的长期在轨自主定轨。

［1］ 杨 磊.风云二号气象卫星图像自动几何精校正［J］.计算机工程与应用，2011，47（3）：202-209.

［2］ 杨 磊，杨忠东.极轨气象卫星自动地标导航方法［J］.应用气象学报，2009，20（3）：329-335.

［3］ 余家祥，萧德云，秦东兴.基于等高地面控制点的航空摄像机参数估计［J］.光学精密工程，2007，15（3）：350-355.

［4］ 陈大志，张广军.基于地标图像信息的惯导系统误差校正方法［J］.北京航空航天大学学报，2003，29（1）：79-82.

［5］ GASKELL R.Landmark navigation studies and target characterization in the hayabusa encounter with Itokawa［R］.AIAA，2006-6660.

［6］ ELLIS K.GOES-R advanced baseline imager image navigation and registration［C］.5thGEOS Users’Conference，P1：27.