火箭发动机双向摇摆机构运动学研究

钱昌年，傅俊勇，张 亮，朱康武

（上海航天控制技术研究所，上海 200233）

0 引言

火箭发动机摇摆机构是火箭控制系统的执行机构，其作用是响应控制系统的指令，通过调整发动机姿态改变发动机推力方向，从而实现调整箭体的姿态。双向摇摆火箭发动机采用2台伺服机构进行摆动控制，实质上构成了一种空间二自由度并联机构。根据伺服机构的伸缩位移求取发动机的空间姿态是火箭姿态控制设计的必要环节，传统采用近似线性化方法处理［1］。某新型双向摇摆发动机由于伺服机构支点与摇摆点不在一个平面内，采用传统方法设计忽略了火箭发动机摆角的正负不对称性和俯仰摆角与偏航摆角的互相干扰，存在较大的误差，需从并联机构的角度考虑火箭发动机摆角解析解求取问题。并联机构运动学正向求解指在已知机构输入关节的条件下求解机构末端的位置和姿态，反向求解指在已知机构末端位置和姿态的条件下求解机构的输入关节变量。因并联机构的正向运动学方程具高阶非线性特点，求解过程非常复杂［2］。一般，并联机构的运动学正向求解远难于反向求解，正解多采用数值解法［3］。本文对新一代运载火箭发动机双向摇摆机构运动学进行了研究。

1 系统描述

新一代运载火箭并联双向摇摆机构主要由发动机，电液伺服机构A、B，动支架，常平架（与箭体固连）等组成，如图1所示。常平架与动支架以及动支架与发动机间分别由两个互相垂直的铰链连接，两个铰链关节的轴线相交于点O，发动机能绕旋转中心O作自由度定点转动。发动机摇摆运动由2台电液伺服机构驱动，其上下支点分别通过球铰链与发动机喷管和常平架连接。伺服机构与发动机的铰接点分别为A，B；伺服机构与常平架的铰接点分别表示为OA，OB；平面OAOA垂直于平面OBOB。

图1 发动机并联双摇摆机构（初始姿态）Fig.1 Parallel two－way swiveling mechanism of launcher engine（initial configuration）

为描述发动机姿态，定义以下坐标系。

a）坐标系O－xyz：固连于常平架，xOy平面与水平面平行，Ox轴位于平面OAOA；Oy轴位于平面OBOB。分别定义发动机绕Ox，Oy轴的转角为俯仰角和偏航角，发动机姿态控制算法设计中主要考虑这两者。

b）坐标系O－x1y1z1：固连于常平架，由O－xyz系绕Oz轴逆时针旋转45°而得，Ox1轴为连接动支架和常平架的铰链轴线；Oy1轴为连接发动机和动支架的铰链轴线。

c）坐标系O－x2y2z2：固连于动支架。

d）坐标系O－x3y3z3：固连于发动机喷管。

发动机在任意时刻的姿态可描述为：O－x3y3z3系和O－x2y2z2系在零位姿态与O－x1y1z1系重合，发动机连体坐标系先绕Ox1轴转动α，再绕Oy2轴转动β，如图2所示。如已知发动机两个铰链转角α，β，就可通过转换得到发动机的俯仰角和偏航角（即发动机绕Ox，Oy轴的转角）。

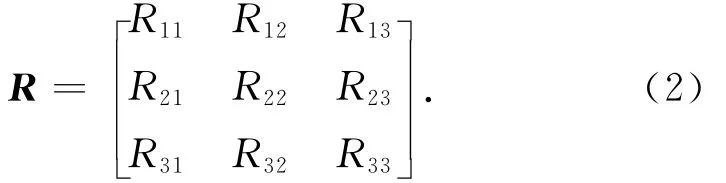
用旋转矩阵表示坐标系间的相对方位［4］。O－x3y3z3系相对O－xyz系的方位可表示为

式中：

图2 发动机姿态Fig.2 Description for configuration of engine

展开式（1），可得

式中：nA，nB分别为n′A，n′B在O－xyz系中的表示。在O－xyz系中定义矢量

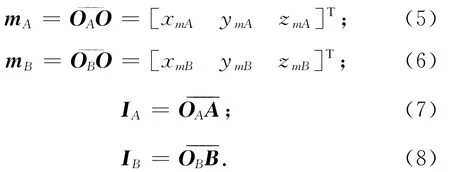
2 运动学正解

将两台伺服机构作动筒的伸缩量ΔlA，ΔlB分别作为发动机并联双摇摆机构的两个主动输入，发动机的两个铰链转角α，β为发动机摇摆机构的输出（或是发动机俯仰角和偏航角）。发动机双摇摆机构的运动学正解是已知ΔlA，ΔlB求发动机转角α，β。因现有火箭发动机不具备转角传感器，发动机的姿态只能由伺服机构作动筒的伸缩量求得，故有必要求解摇摆机构正向运动学问题。

在O－xyz系中，存在关系

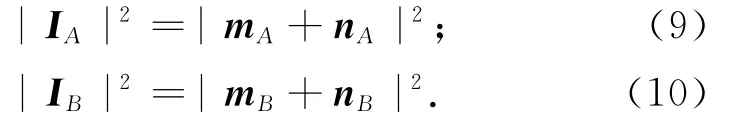
式中：｜IA｜2＝（lA0＋ΔlA）2；｜IB｜2＝（lB0＋ΔlB）2。此处：lA0，lB0分别为已知的两台伺服机构的初始长度。当给定输入ΔlA，ΔlB时，式（9）、（10）左边为已知量，此即火箭发动机并联双摇摆机构的运动约束方程。将式（2）～（8）代入式（9）、（10）并展开，可得关于α，β的一组方程

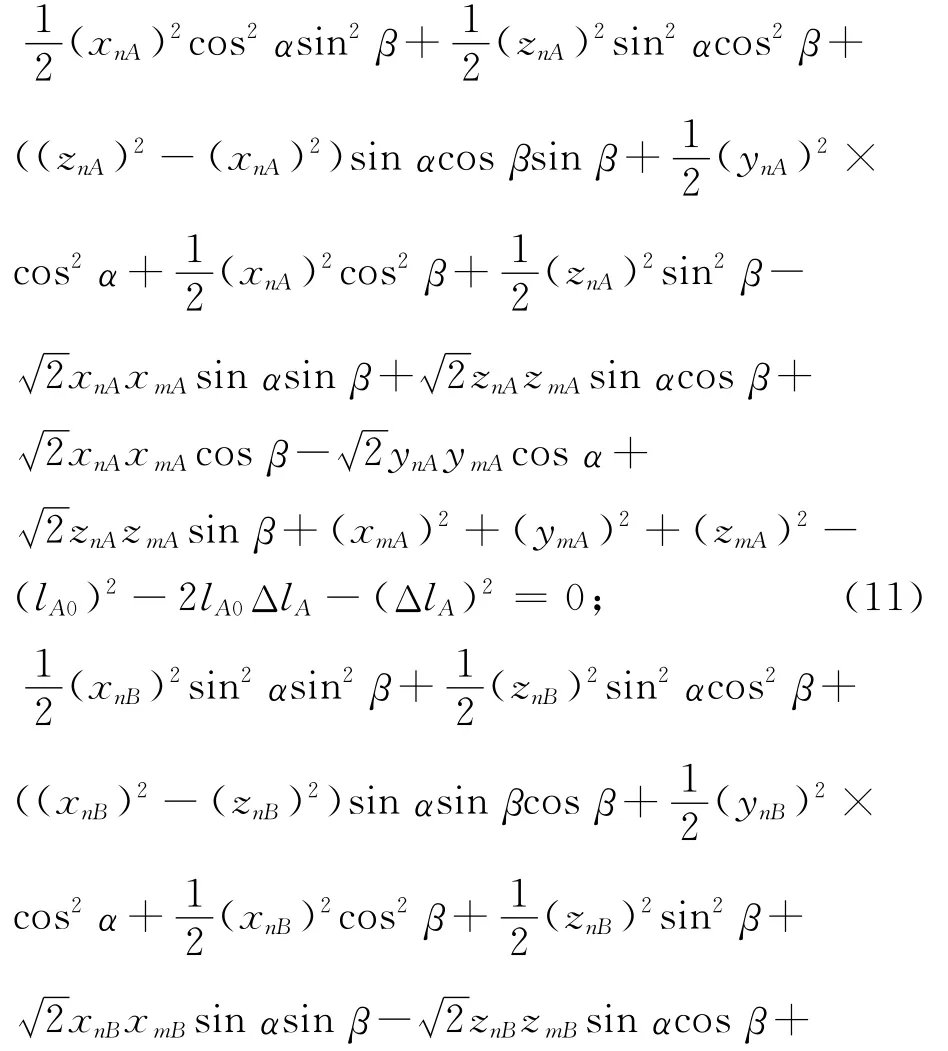
式（11）、（12）中只有α，β是未知量，其他参数均为结构已知参数。式（11）、（12）是关于α，β超越方程，为便于求解，将半角公式

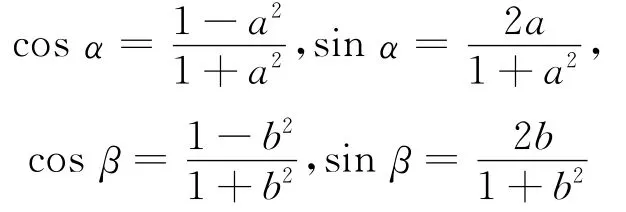
代入式（11）、（12），整理后得

成立［5］。化简后可得关于a的16次方程

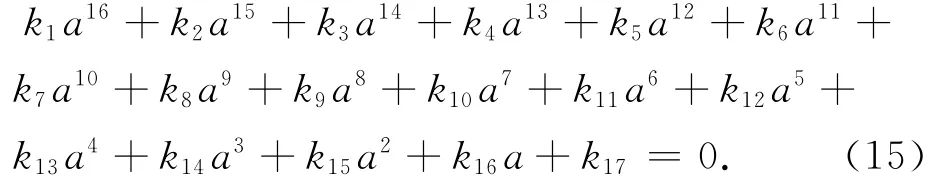
式中：k1，k2，…，k17为已知参数的表达式。

用上述方法消去未知量b，将一组二元高次方程组转为一元高次方程组，求解方程（15）可得a的16个解。此即求解高次方程的Sylvester消元法，但求解过程中需剔除引入的无效解。

式（15）是式（13）、（14）存在共同解的必要条件，并非所有a的实数解都能使式（13）、（14）同时成立。分别将a的实数解代入式（13）、（14），每个a的实数解都能由式（13）、（14）解出两组b的解（每组4个），若两组b的解中有相等的，则说明当前a为有效解，否则舍去。根据发动机并联双摇摆机构结构特点，如不考虑运动范围，对每一组输入 ｛ΔlA，ΔlB｝，发动机均有两个姿态满足约束条件（发动机喷管朝上或朝下），故对一组输入 ｛ΔlA，ΔlB｝，均能由式（13）～（15）确定两组有效的｛a，b｝，对每个a或b的实数解，都能在［0°，360°］唯一确定α＝2arctana，β＝2arctanb，即可由两组｛a，b｝确定两组｛α，β｝。实际发动机只限定在喷管朝上（图1为发动机实验环境，实际发动机喷管朝下）的范围内运动，且发动机在运行过程中α，β∈（－10°，10°），由这些条件可在一系列求解结果中筛选出唯一解。在求解唯一解时，先判定解的有效性，再判断解是否处于运动范围内，也可调换两个过程的顺序，能有效减少求解高次方程的次数。

设发动机双摇摆机构结构参数为

令输入｛ΔlA，ΔlB｝＝｛－60mm，105mm｝，将参数代入式（15），可得

求解并舍去复 数 解，有a1＝－1.980 2，a2＝－0.065 9，a3＝0.058 0，a4＝5.406 6，与之相应的α解 为α1＝－126.413 5°，α2＝－7.539 5°，α3＝6.633 6°，α4＝159.042 1°。显然只有α2，α3在运动范围（－10°，10°）内，舍去其余解，为剔除无效解，将a2＝－0.065 9分别代入式（13）、（14）求解并舍去复数解，分别得b1＝－5.055 0，b2＝0.099 3；b1＝－3.205 5，b2＝－0.157 2。可知a2＝－0.065 9不能使式（13）、（14）同时成立，为无效解。将a3＝0.058 0分别代入式（13）、（14），求解并舍去复数解，分 别 得b1＝ －5.635 9，b2＝－ 0.018 0；b1＝－3.172 0，b2＝－0.018 0。判断可知a3＝0.058 0，b2＝－0.018 0是式（13）、（14）的一组共同解，则β＝－2.062 4°，处于有效运动范围内。由此，当输入为｛ΔlA，ΔlB｝＝｛－60mm，105mm｝时，发动机的铰链转角 ｛α，β｝＝ ｛6.633 6°，－2.062 4°｝。

3 运动学反解

发动机并联双摇摆机构的运动学反解，就是在已知发动机姿态（即已知铰链转角α，β）的前提下求解两台伺服机构作动筒的伸缩量，即已知发动机推力矢量的方向 ｛α，β｝求 ｛ΔlA，ΔlB｝，摇摆机构运动学反解直接用于火箭姿态控制算法。与运动学正向求解过程相比，运动学反向求解简单。简化式（9）、（10）并将已知参数代入，可得

式中：LA，LB（＞0）为已知参数的函数表达式，其物理意义为电液伺服机构的总长度，且

由｜lA｜＝lA0＋ΔlA，｜lB｜＝lB0＋ΔlB，可得运动学反解 ΔlA＝LA－lA0，ΔlB＝LB－lB0。此处：lA0，lB0分别为两台伺服机构的初始长度。

将 上 述 运 动 学 正 解 ｛α，β｝ ＝ ｛6.633 6°，－2.062 4°｝代 入 式 （16），（17）可 得LA＝1 782.885 5mm，LB＝1 947.990 9mm，与之对应的｛ΔlA，ΔlB｝＝｛－60.114 5mm，104.990 9mm｝，该结果与上述正向求解的输入值｛ΔlA，ΔlB｝＝｛－60mm，105mm｝基本一致。

4 SimMechanics仿真验证

为验证运动学正向求解算法在整个发动机运动范围内的有效性和精度，根据发动机并联双摇摆机构的物理和几何关系，在SimMechanics环境中建立验证模型，在表1两种输入条件下对机构模型进行计算和仿真，结果如图3～6所示［6］。

图3 ΔlA＝－10mm时αFig.3 Calculating and simulation values of αatΔlA＝－10mm

图4 ΔlA＝－10mm时βFig.4 Calculating and simulation values of βatΔlA＝－10mm

由图可知：计算和仿真结果几乎完全重合，证明计算结果和模型正确。其中α，β的误差量级分别为10－4，10－3（β的误差大于α的原因是求解β过程中多次截断误差累加），该误差级别远小于机构弹性变形和加工工艺导致的误差，由此可见本文计算方法有充分的精度。

图5 ΔlB＝－8mm时αFig.5 Calculating and simulation values of αatΔlB＝－10mm

图6 ΔlB＝－10mm时βFig.6 Calculating and simulation values of βatΔlB＝－10mm

表1 两种输入条件Tab.1 Two input conditions

5 线性化方法误差分析

某新型火箭研制过程中，用传统线性化方法处理摇摆机构伺服作动筒伸缩位移和发动机俯仰角与偏航角关系，即简单认为伺服机构最大伸缩量110mm对应于发动机偏航角或俯仰角最大值6.5°，伺服机构最小伸缩量－110mm对应于发动机偏航角或俯仰角最小值－6.5°，将两者视为比例关系，其处理必存在误差。另外，由于发动机摇摆中心与伺服机构支点不在一个平面，发动机俯仰角和偏航角存在干扰。

在图1中，当俯仰伺服机构B推动发动机运动时，发动机绕Ox，Oy轴均有转动，即俯仰伺服机构的运动对发动机俯仰角和偏航角都有作用，偏航伺服机构亦是如此。传统近似处理方法忽略了伺服机构运动对另一个转角的影响。在表1输入条件下分析上述近似线性化方法存在的误差，结果如图7～10所示。由图可知：俯仰角（θx）和偏航角（θy）用近似线性化方法计算的结果存在较大误差，且偏差随输入值增大而变大，最大偏差为0.4°／6.5°＝6.15%。

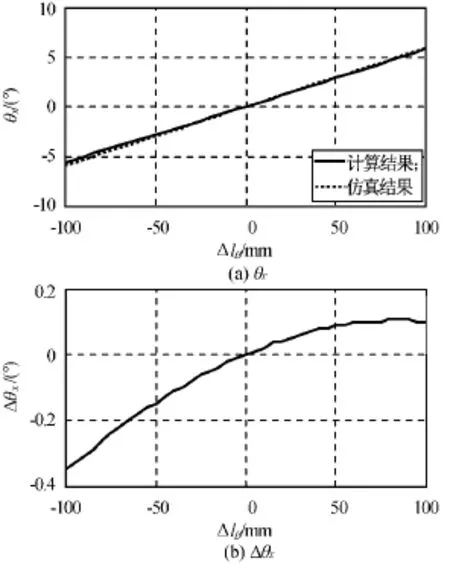
图7 ΔlA＝－10mm时θxFig.7 Calculating and simulation values of θxatΔlA＝－10mm

图8 ΔlA＝－10mm时θyFig.8 Calculating and simulation values of θyatΔlA＝－10mm

图9 ΔlB＝－8mm时θxFig.9 Calculating and simulation values of θxatΔlB＝－8mm

图10 ΔlB＝－8mm时θyFig.10 Calculating and simulation values of θyatΔlB＝－8mm

6 结束语

本文对火箭发动机并联双摇摆机构进行了运动学分析，根据机构物理构成特点，用矢量方法列出了运动约束方程，引入半角公式并用Sylvester消元方法得到了一元16次方程，给出了运动学正向求解方法，并导出了运动学反解的解析表达式。SimMechanics建模仿真验证结果证明运动学正向求解方法正确。用本文方法分析了现有线性化近似计算方法的误差。研究可为火箭控制系统设计提供参考。

［1］ 朱忠惠.推力矢量控制伺服系统［M］.北京：宇航出版社，1995：360－376.

［2］ PETUYA V，GUTIERREZ J M，ALONSO A，et al.A numerical procedure to solve non－linearkinematic problems in spatial mechanism［J］.International Journal for Numerical Methods in Engineering，2008，73（6）：825－843.

［3］ 黄 真.高等空间机构学［M］.北京：高等教育出版社，2006：141－146.

［4］ 蔡自兴.机器人学［M］.北京：清华大学出版社，2000：46－51.

［5］ 罗佑新.机构综合的结式消元法及其 MAPLE实现［J］.纺织学报，2005，26（2）：79－81.

［6］ 王英波，黄其涛，郑书涛，等.Simulink和SimMechanics环境下并联机器人动力学建模与分析［J］.哈尔滨工程大学学报，2012，33（1）：100－105.