基于极端风险假设的风电并网调峰充裕度评估

谢绍宇，蒋健

（广州供电局有限公司，广东 广州 510620）

基于极端风险假设的风电并网调峰充裕度评估

谢绍宇，蒋健

（广州供电局有限公司，广东 广州 510620）

针对大规模风电并网给电力系统带来的有功平衡困难，结合实际运行中偏保守的调度策略，提出一种基于极端风险假设的风电并网调峰充裕度评估方法。假设风功率预测完全不可靠，分析了含风电系统的最大调峰需求；假设各时段风功率为零，进行日前机组组合，确定峰荷时段的最大开机方式，再结合机组调峰深度，分析了调峰容量的供给。应用序贯蒙特卡洛模拟技术进行调峰充裕度评估。算例表明，随着规划风电规模的扩大，系统调峰充裕度指标迅速恶化。将风电装机容量分散到具有相关性的多风电场将显著减轻系统的调峰压力。

风电；调峰充裕度；序贯蒙特卡洛；机组组合

调峰是制约风电大规模并网应用的主要难题。风电的随机性、波动性有可能使系统等效负荷峰谷差增大，进而增加系统对调峰容量的需求[1-2]。在风功率预测精度不高的情况下，电网企业倾向于采用高备用水平的保守运行方式，而火电机组最小技术出力和最小启停时间反过来又会影响谷荷时段风电的消纳，导致弃风。控制运行风险和提高风电消纳水平成为可再生能源发电并网需要解决的主要矛盾。

为了应对电力系统调峰，发电设备定期检修及机组的随机故障，系统通常会配置一定的备用容量。调峰可以看作备用容量[3]概念的一部分，即调峰是为应对负荷变化而有计划地调用系统备用容量的过程。在含风电的电力系统中，既存在负荷较高时段风功率不足，需要常规机组向上调出力、使用正备用的情况，也存在负荷低谷时段风功率过大，需要常规机组向下压出力、调用负备用的情况。调峰需求实质上是对机组有功出力双向调节的深度和灵活性的需求。

针对大规模风电接入后系统调峰容量需求评估的难题已有大量研究工作。文献[4]计算了特定可靠性水平对应的备用容量，根据低谷常规机组调峰能力评估电网接纳风电能力。文献[5]通过电源调峰能力分析得到每日各时段的风电接纳空间，然后根据弃风功率时序曲线统计各类弃风指标。文献[6]从辅助服务价值的角度出发，区分火电机组的基本调峰服务和有偿调峰服务，提出考虑风电并网的有偿调峰服务成本分析模型。文献[7-8]对风功率预测精度进行分类，探讨它们对系统调峰需求的影响，并重新定义了调峰需求和调峰充裕度指标，以获取系统调峰裕度信息，为校验风电规划方案提供指导。然而，文献[7-8]事先指定了每天常规机组可用与否的状态，没有考虑日前开机计划对“哪些机组真正参与了调峰”的影响；也仅考虑了单一风电场的情况，没有计及多风电场风速时空相关性和互补性[9-10]对调峰裕度的影响。

在风功率预测精度没有重大突破的现状下，对风险敏感的电网还是倾向于采用偏保守的调度策略。因此，本文将基于2个“悲观假设”提出一种风险敏感的调峰充裕度评估方法：

1）假设日前风功率预测完全不可靠从而最大化调峰需求。

2）基于忽略风电出力的日前机组组合（unit commitment，UC）确定参与调峰的常规机组。基于调峰需求侧和供给侧的保守假设分析，更有利于风险厌恶的实际运行人员的认知和应用。同时，本文还将分析多风电场场景下风速相关性对系统调峰充裕度的影响，为风电装机规划决策提供有益的参考。

1 风电并网的调峰需求与供给

1.1 调峰需求分析

图1展示了风电并网前后调峰需求的确定方法，其中tv和tp为系统谷荷、峰荷对应的时段，负荷值分别为Pmin、Pmax风电容量为PW。在不含风电时，所有开机的常规机组的有功出力总和应满足峰荷Pmax，在谷荷时段tv应满足Pmin。这就要求系统在Pmax与Pmin之间具有一定的灵活可调节容量Pab，这部分容量通常由开机机组的可调出力区间和允许启停的机组容量组成。因此，根据负荷需求曲线P（t），可以确定风电接入前系统的调峰需求曲线为P（t）-Pmin。

图1 风电并网前后的调峰需求Fig.1 The peak regulation requirements before and after the integration of wind power

装机容量为PW的风电场接入系统后，在风功率预测完全不可靠的极端保守假设下，需要考虑以下2种情况：

1）在峰荷时段tp风电出力为零，常规机组的有功出力总和应承担峰荷Pad。

2）在谷荷时段tv风电满发，为了避免弃风，常规机组总出力应承担Pcd。

因此，常规机组可调整的容量（包括已开机、可上下调整出力的火电机组和可随时启停的各类机组）必须覆盖区间Pad-Pcd=Pac=（Pmax-Pmin）+PW，这是全天最大调峰需求。类似地，在“谷荷时刻风电可能满发”的逆调峰极端假设下，峰荷以外时段t风电出力可能为零，因此调峰需求为：

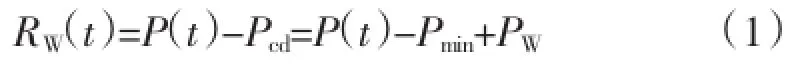
由于采用了风功率预测完全不可靠的极端假设，式（1）是t时段可能存在的最大调峰需求，反映了风险厌恶的决策者规避风电不确定性、谋求绝对可靠的风险心理。

1.2 调峰供给分析

接下来考虑由哪些资源提供调峰能力来满足式（1）中的调峰需求RW（t），将分析范围局限于发电侧，不考虑负荷侧资源。设系统中常规机组集合为G，编号为i。逻辑变量ui（t）为机组i在t时段的启停状态，1为开机，0为停机。

火电机组运行的技术特性决定了其可灵活调节的出力区间（即调峰深度）有限。文献[6]定义了各类机组的调峰容量比：

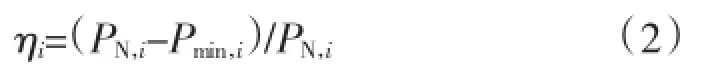
式中：ηi、PN，i和Pmin，i分别为第i台机组的调峰容量比、额定容量和最小技术出力。

有调节能力的水电和燃气、燃油机组可快速启停，调峰容量比为1；无调节能力水电、热电联产及核电机组一般满发承担基荷，调峰容量比为0。

结合图1，调峰需求RW（t）应该由以下3部分共同满足：

1）可灵活启停的机组提供一定的有功出力弹性：

2）已开机的大型火电机组提供一定的可调容量。由于实际运行中，大型火电机组日内一般不启停，日前确定的峰荷时段的开机组合（即最大开机方式）在1 d中一般都保持开机。

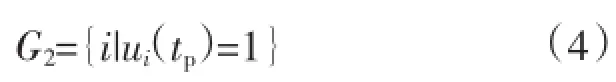
2 调峰充裕度评估

本文将从风险规避的观点来分析系统满足调峰需求PW（t）的能力。忽略负荷预测的不确定性，考虑参与调峰的中机组的强迫停运和风功率的随机性，采用概率性方法评估调峰充裕度。

2.1 根据日前UC确定参与调峰机组

利用日前UC确定G2。同样基于较保守的风险态度，在完整约束的UC中认为日前风功率预测完全不可靠，将1天24 h的风电出力取零，但也相应地不设置旋转备用约束。这样得到的峰荷时段的开机组合为最大开机G2方式，认为这时在线的大型火电机组在当天其他时段也保持开机。求解G2的UC的完整数学模型可参阅文献[11]，这里略去。

2.2 序贯蒙特卡洛模拟

采用序贯蒙特卡洛模拟评估系统在1 d中各个时段的调峰充裕度。假设调峰充裕度测度函数为g（·），发电系统某抽样状态sjt（系统中各机组正常运行与否的状态）的持续时间为D（sjt），总模拟天数为N。第j天经历的系统状态序列为共 Nj个状态（一般以1 d为周期、1 h为时间尺度研究调峰问题，故本文取Nj=24）。抽样第j天所得调峰充裕度指标为

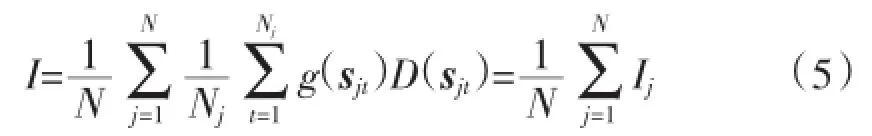
如果取

那么，I为调峰不足概率（loss of peak load probability，LOPLP），记为ILOPLP；

如果取

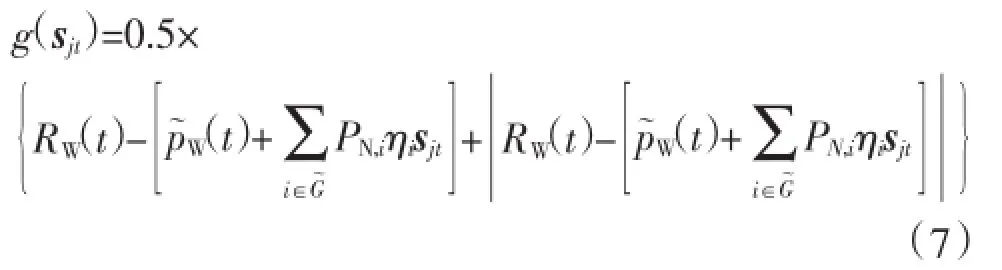
那么，I为调峰电量不足期望值（expected peak energy not supplied，EPENS），记为IEPENS。在恒定时间步长抽样中，D（sjt）一般取为1 h。

2.3 收敛性判别

类似于传统的可靠性指标，调峰充裕度指标I的标准差的无偏估计量为[13]：

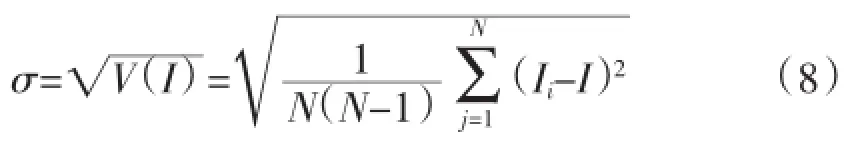
收敛性一般用指标I的方差系数检验：

由于SMCS是一个波动收敛的过程，β能够反映样本均值与理论均值之间的误差，误差越小则模拟精度越高，但计算消耗越大，应综合权衡。

3 算例分析

3.1 算例简介

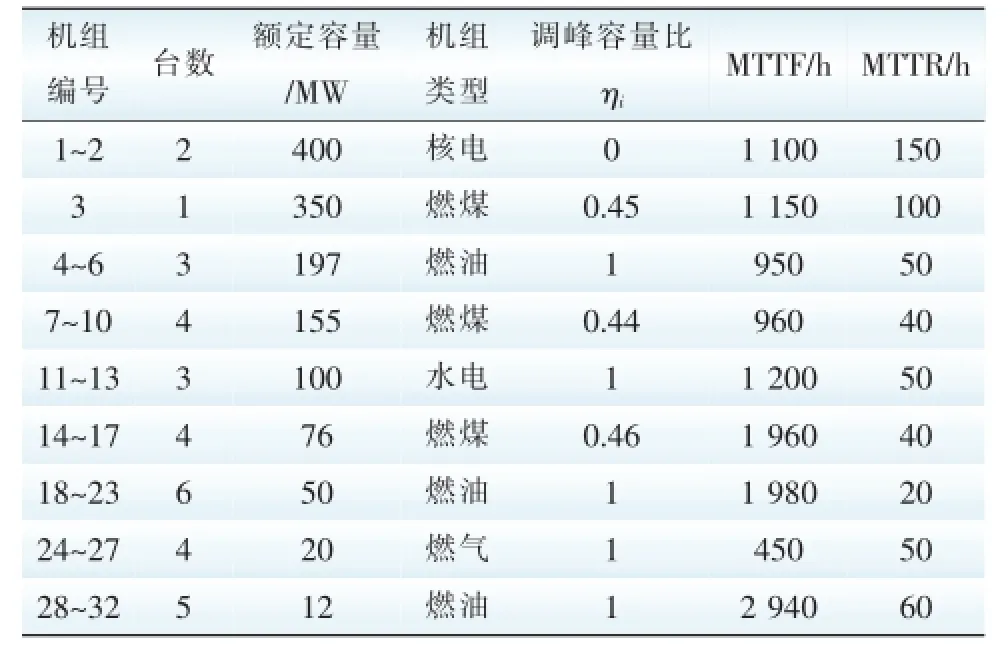
表1 IEEE-RTS79发电机组参数Tab.1 Parameters of IEEE-RTS79 generating units

算例采用IEEE-RTS79系统[14]，32台机总装机容量为3 405 MW，最大单台机组容量为400 MW，机组参数列于表1，其他参数可参阅文[15]。系统一典型日负荷曲线（标幺值）如表2所示，负荷基准值取为2 850 MW，从而该日的峰值负荷为2 308.5 MW，日负荷峰谷差为847 MW。将风电机组集群接入风电场，以整个风电场为单位，在某地实测风速数据[16]的基础上，通过自回归滑动平均法（auto-regressive moving average，ARMA）来模拟风速。根据实测数据建立的ARMA模型为：

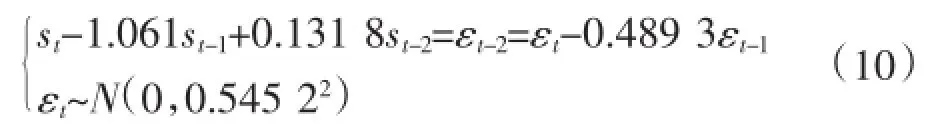
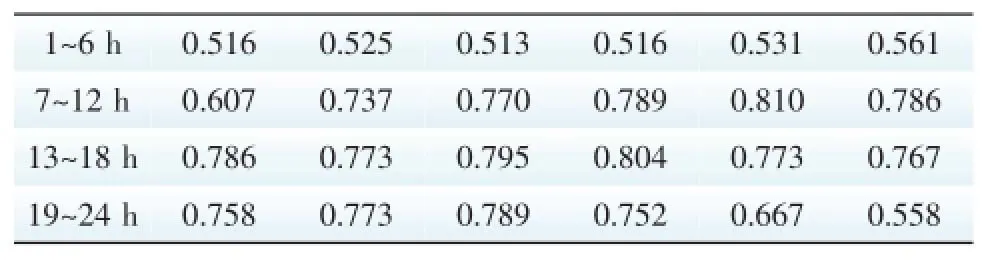
表2 时序负荷曲线Tab.2 Sequential load curve pu

在后文分析中将采用该模拟对风速进行模拟。

为了对比所提确定参与调峰的火电机组G2的方法与已有方法[8]的不同，构建2种情形。

情形1：任意指定开机组合，认为所有机组的调峰能力都可用。

情形2：根据保守的日前UC确定的峰荷时段开机组合确定该日可用的调峰机组。

3.2 利用日前UC确定开机计划

为了抵御风电出力不确定的风险，日前UC中不进行风功率预测，而是认为各时段风电出力都为零，谋求包络各种运行风险。得到1天24 h各机组的启停计划如图2所示，其中横轴表示1天内24个时段，纵轴为32台机组的编号（见表1），实心黑点表示该机组在该时段处于开机状态。应特别关注峰荷时段11时的开机情况。

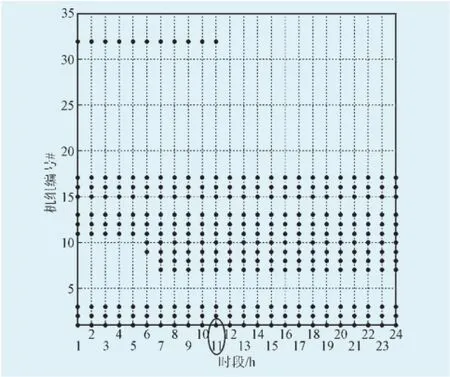
图2 日前开机计划Fig.2 Day-ahead unit commitment

可以看出，峰荷时段tp=11 h在线的机组包括，因此，可以确定为简化起见，假设峰荷时段开机的大型火电机组在日内均不启停，它们在1 d中各时段向上或向下调节出力以提供调峰深度。也就是说，在这1天中除了机组14号（因为在这1 d中14号根本没有开机且不具备快速启停能力）以外的其他机组均能在不同程度上提供调峰服务。在忽略机组强迫停运的情况下，常规机组提供的可调容量总计为1866MW，在不接入风电时超出系统最大调峰需求847 MW的120%，调峰容量是充裕的。

中国考古认为：汉水要比长江黄河早七亿多年；人类繁荣起源：地球的北纬30度线为起步线；汉江之滨的陕西安康市幅员正在北纬30度左右，或为人类始祖伏羲和女娲的诞生地。

3.3 收敛性讨论

图3给出了PW=1 000 MW时调峰不足概率指标ILOPLP的波动收敛过程。随着模拟天数的增加，ILOPLP逐渐趋近于理论均值。

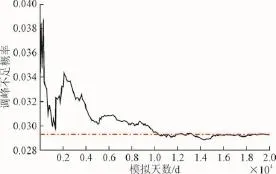
图3 调峰不足概率的收敛过程Fig.3 The convergence progress of the IL0PLP

图4给出了2种调峰充裕度指标的方差系数收敛曲线。当样本容量达到2×104d时，方差系数被控制到3%以内且基本不再变化，符合精度要求。与可靠性指标相似，概率指标比电量指标更容易收敛。

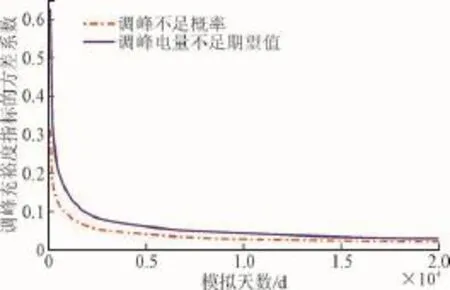
图4 方差系数随模拟天数变化曲线Fig.4 The coefficient of variation as a function of the number of samples

3.4 系统调峰充裕度分析

将不同额定容量的风电场接入IEEE-RTS79系统，分别评估系统的调峰充裕度。图5给出了2种情形下，对不同的风电装机容量，系统的调峰不足概率。从图5可以看出，当风电规模控制在0～600 MW时，2种情形下系统的调峰不足概率一直为0，调峰容量充裕。随着风电规模的扩大，2种情形下的ILOPLP都逐步上升。

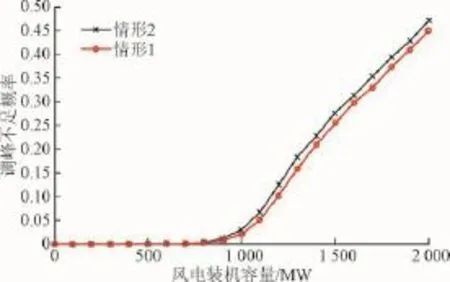
图5 不同风电装机规模下的系统调峰不足概率Fig.5 The IL0PLPunder different rated wind capacities

当风电规模增大至1 100 MW以上时，系统的ILOPLP快速上升，并且情形2下的调峰不足概率明显高于情形1——即由日前UC所得开机组合确定的参与调峰机组，将导致评估结果呈现更高的风险，表现得更为审慎。这是因为任意指定开机组合的方法认为14号机组也可以参与调峰，而事实上在日前按照最恶劣的假设（风电一直零出力）确定的开机计划中，14号机组并没有开机且不能快速启停，现实中不可能参与调峰。因此的系统实际调峰风险要高于认为的情况，未确定最优开机方式就任意指定哪些机组可以参与调峰的方法是偏离实际的。

可以看到，当风电装机容量增至2 000 MW时，2种情形下的ILOPLP分别高达0.470 9和0.448 9，系统存在严重的调峰困难。越大的风电装机规模要求越多的调峰资源，在系统现有有限的供给能力下，表现为越严重的供需不平衡和越高的调峰风险。

图6给出了2种情形下，调峰电量不足期望值随着风电规模的扩大而变化的曲线。类似地，当风电装机控制在0～600 MW时，系统不存在调峰电量损失。当风电规模超过1 000 MW时，系统的IEPENS迅速上升，并且也能观察到任意指定开机组合时对风险的估计偏低——因为不恰当地认为14号机组也能参与调峰。当风电规模达到2 000 MW时，2种情形下系统调峰电量损失期望分别高达5 337 MW·h/d和4 915 MW·h/d，存在较大的调峰风险。

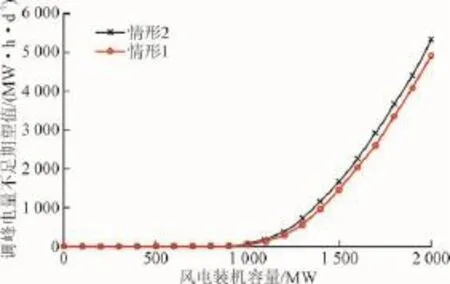
图6 不同风电装机规模下的系统调峰电量不足期望值Fig.6 The IEPENSunder different rated wind capacities

本节考虑多个风电场之间的相关性对系统调峰充裕度指标的影响。取同一测风塔相邻日的实测风速，作为不同空间位置的风电场同一天的实测风速。表3列出了不同风电装机容量由多个风电场组成的情况下，系统的调峰不足概率和调峰电量不足期望值指标。横向比较可以看出，随着风电装机容量增大，调峰充裕度都迅速恶化。纵向比较可以看出，一个装机1 000 MW的风电场，比5×200 MW的风电场，给系统带来显著更大的调峰难度；不同位置的5个400 MW的风电场，较之于10个200 MW的风电场，调峰风险要大很多。这说明同样的风电装机容量，空间分布越分散，风电场数越多，系统的调峰压力越小。这是因为多个风电场之间风功率体现一定的互补性，削减了总风功率的波动性和间歇性，使出力较之单个风电场更为平稳，从而更好地满足系统的调峰需求。

表3 不同装机容量、多个风电场对系统调峰充裕度指标的影响Tab.3 Impacts of different wind generation capacities and multi wind farms on the system peak-regulation adequacy indices

4 结语

本文从运行人员风险厌恶的心理出发，完善了一种基于极端风险假设的大规模风电并网后系统调峰充裕度分析方法。极端风险假设体现在：

1）分析调峰需求时认为风功率预测完全不可靠，最大化调峰需求以包络风功率的所有情形；

2）日前认为风功率一直为零来确定最大开机计划，以确定实际参与调峰的机组。

算例分析表明：

1）随着规划风电装机规模的增大，系统的调峰风险显著上升，需要配套更多的调峰资源。

2）从调峰充裕度的角度出发，在现有常规电源装机下，将风电的规划容量分散到具有相关性的多风电场，会显著减轻调峰压力。

3）调峰充裕度指标可以作为可靠性指标的有益补充，在那些需要可靠性评估的场合，可应用调峰充裕度指标以突出对系统调峰能力的考虑。另外，在考虑电源长期扩建计划时，以本文方法评估调峰风险，进行综合的成本收益分析，可以指导配备适当水平的调峰资源。

[1]吴俊，李建设，周剑，等.风力发电并网对电网的影响[J].南方电网技术，2010，4（5）：48-52. WU Jun，LI Jianshe，ZHOU Jian，et al.Influence of wind power generation integrating into power grids[J].Southern PowerSystemTechnology，2010，4（5）：48-52（in Chinese）.

[2]周鑫，张慧玲，刘娟楠.大规模风电接入对宁夏电网调峰的影响研究[J].电网与清洁能源，2014，3（2）：105-110. ZHOU Xin，ZHANG Huiling，LIU Juannan.Impacts of 1arge-scale grid-connected wind power on peak regulation in ningxia grid[J].Power System and clean Energy，2014，3（2）：105-110（in Chinese）.

[3]王若谷，王建学，张恒，等.水电机组调峰服务的成本分析及实用补偿方法 [J].电力系统自动化，2011，35（23）：41-46. WANG Ruogu，WANG Jianxue，ZHANG Heng，et al.A cost analysis and practical compensation method for hydropower units peaking service[J].Automation of electric Power Systems，2011，35（23）：41-46（in Chinese）.

[4]孙荣富，张涛，梁吉.电网接纳风电能力的评估及应用[J].电力系统自动化，2011，35（4）：70-76. SUN Rongfu，ZHANG Tao，LIANG Ji.Evaluation and application of wind power integration capacity in power grid[J].Automa-tion of electric Power Systems，2011，35（4）：70-76（in Chinese）.

[5]吕泉，王伟，韩水，等.基于调峰能力分析的电网弃风情况评估方法[J].电网技术，2013，37（7）：1887-1894. LÜ Quan，WANG Wei，HAN Shui，et al.A new evaluation method for wind power curtailment based on analysis of system regulation capability[J].Power System Technology，2013，37（7）：1887-1894（in Chinese）.

[6]张钦，辛颂旭，白建华，等.西北地区促进风电消纳的辅助服务市场机制研究[J].中国电力，2013，46（7）：111-115. ZHANG Qin，XIN Songxu，BAI Jianhua，et al.Study of ancillary service market mechanism for the promotion of wind power consumption in northwest region[J].electric Power，2013，46（7）：111-115（in Chinese）.

[7]张宏宇，印永华，申洪，等.大规模风电接入后的系统调峰充裕性评估[J].中国电机工程学报，2011，31（22）：26-31. ZHANG Hongyu，YIN Yonghua，SHEN Hong，et al. Peak-1oad regulating adequacy evaluation associated with 1arge-scale wind power integration[J].Proceedings of the CSEE，2011，31（22）：26-31（in Chinese）.

[8]张宏宇，印永华，申洪，等.基于序贯蒙特卡洛方法的风电并网系统调峰裕度评估[J].电力系统自动化，2012，36（1）：32-37. ZHANG Hongyu，YIN Yonghua，SHEN Hong，et al.Peakshaving margin evaluation associated with wind power integrated system based on sequential monte-carlo method[J]. Automation of electric Power Systems，2012，36（1）：32-37（in Chinese）.

[9]蔡菲，严正，赵静波，等.基于Copula理论的风电场间风速及输出功率相依结构建模[J].电力系统自动化，2013，37（17）：9-16. CAI Fei，YAN Zheng，ZHAO Jingbo，et al.Dependence structure models for wind speed and wind power among different wind farms based on copula theory[J].Automation ofelectricPowerSystems，2013，37（17）：9-16（in Chinese）.

[10]黎静华，文劲宇，程时杰，等.考虑多风电场出力Copula相关关系的场景生成方法[J].中国电机工程学报，2013，33（16）：30-36.

LI Jinghua，WEN Jinyu，CHENG Shijie，et al.A scene generation method considering copula correlation relationship of multi-wind farms power[J].Proceedings of the CSEE，2013，33（16）：30-36（in Chinese）.

[11]CARRIÓN M，ARROYO J M.A computationally efficient mixed-integer 1inear formulation for the thermal unit commitment problem[J].IEEE Trans.Power Systems，2006，21（3）：1371-1378.

[12]赵渊，周家启，刘志宏.大电网可靠性的序贯和非序贯蒙特卡洛仿真的收敛性分析及比较[J].电工技术学报，2009，24（11）：127-133. ZHAO Yuan，ZHOU Jiaqi，LIU Zhihong.Convergence analysis and comparison of sequential and nonsequential monte-carlo simulation for bulk power system reliability assessment[J].Transactions of China electrotechnical Society，2009，24（11）：127-133（in Chinese）.

[13]BILLINTON R，WENYUAN L.Reliability assessment of electric power systems using monte carlo methods[M].New York：plenum，1994：35-36，84-87.

[14]IEEE Task Force.IEEE reliability test system[J].IEEE Transactions on Power Apparatus and Systems，1979，PAS-98（6）：2047-2054.

[15]WANG C，SHAHIDEHPOUR S M.Effects of ramp-rate 1imits on unit commitment and economic dispatch[J].IEEE Trans.Power Systems，1993，8（3）：1341-1350.

[16]Iowa environmental mesonet&iowa state university department of agronomy.Wind speed data from the network of AWOS sensors[DB/OL].2011-04-01.http：//mesonet.agron. iastate.edu/request/awos/1min.php.

（编辑 董小兵）

Peak-Load Regulation Adequacy in Wind-Integrated Systems Based on Extreme Risk Hypotheses Adequacy Assessment

XIE Shaoyu，JIANG Jian
（Guangzhou Power Supply Company Limited，Guangzhou 510620，Guangdong，China）

Integration of a 1arge scale of wind power brings difficulties for power balances of the power system.Based on the conservative dispatching strategy which is adopted in the actual operation，a peak-1oad regulation adequacy analysis method in wind-integrated systems is proposed in this paper according to some extreme risk hypotheses.Assuming the wind power prediction completely unreliable，the maximum peaking demands are identified.Assuming the wind power output is zero，the day-ahead unit commitment is conducted，which will determine the maximum system operation method，and the supply of the peak-1ead regulation is determined after considering the peaking depth of each generating unit.The sequential Monte Carlo simulation is used to verify the proposed method. Numerical results show that with the expansion of the scale of wind power planning，the indexes of the peak-1oad regulation adequacy will deteriorate rapidly.The pressure of the peak-1oad regulation will be significantly reduced as the wind power is scattered in a bigger number of wind farms.

2014-07-22。

谢绍宇（1984），男，博士，主要研究方向为电力系统规划与可靠性评估，变电管理与运行；

蒋 健（1982），男，高级工程师，主要从事变电管理与运行。

1674-3814（2015）08-0088-06

TM614

A

KEY W0RDS：wind power；peak-1oad regulation adequacy；sequential Monte Carlo simulation；unit commitment