电网扰动状态下的机电转子稳定控制方法研究

彭秋红，周昕

（1.平顶山工业职业技术学院 自动化与信息工程学院，河南 平顶山 467000；2.平顶山工业职业技术学院网络教育学院，河南 平顶山 467000）

电网扰动状态下的机电转子稳定控制方法研究

彭秋红1，周昕2

（1.平顶山工业职业技术学院 自动化与信息工程学院，河南 平顶山 467000；2.平顶山工业职业技术学院网络教育学院，河南 平顶山 467000）

在对电网扰动状态下的机电转子稳定控制方法的研究过程中，采用当前的方法进行机电转子稳定控制时，转子角行波传输不稳定，控制性能较差。提出基于改进TORA转子位置反馈的机电转子稳定控制方法。该方法依据电网在扰动状态下的特有框架结构，融合FLOYD算法，计算并得到机电设备频率特征函数的变化规律，在此基础上对电网系统稳态时和电网扰动状态下，机电波到达后机电频率的特征进行有效的区分，完成了电网扰动状态下的机电转子稳定控制。实验证明，该方法控制精确度高，稳定性强。

高通滤波器；控制器；FLOYD算法

在电力行业不断发展的同时，电网规模也在快速扩大[1-3]。但随之而来的电网扰动问题也给电力行业带来了严重的危害。而电网扰动状态下的稳定控制方法则是解决这一问题的关键，引起了很多专家与学者的重视[4-6]。其中，电网扰动状态下的机电转子稳定控制在一些领域得到了较好的应用，也成为了业内人士研究的焦点课题，受到了广泛的关注，同时也出现了很多好的方法[7]。

文献[8]提出了将动力学转换为反馈形式的非线性级联来实现对电网扰动状态下的机电转子稳定控制。该方法较为简单，但是存在局限性大的问题。文献[9]重点研究了通过自调节模糊滑模控制实现电网扰动状态下的机电转子稳定控制。该方法耗时短，但是进行机电转子稳定控制时，转子角增量行波传输不稳定，存在控制性能不稳定的问题。文献[10]依据径向悬浮力与偏心位移的相互关联性，使机电对转子偏心位移进行直接控制，完成了电网扰动状态下的机电转子稳定控制。该方法适应性较强，但是计算较为繁琐，存在耗时较长的问题。

针对上述问题的产生，提出了一种基于改进TORA转子位置反馈算法，在电网扰动状态下，应用到了机电转子稳定控制中。

1 扰动状态下的机电转子稳定控制问题分析

一般情况下，电网扰动包含短路与切机/切负荷2种类型。当相关设备的定子连接到电网时，机电转子会由电压型交-直-交PWM变流器配备三相转差频率电流进行励磁。电网扰动状态下的机电转子稳定控制过程中，需要高频率的调节机电转子励磁电流的幅值、频率和相位，使得电网在扰动状态下发电机可以在同步速上、下大范围内做变速恒频运行，完成对有功、无功的解耦控制。具体的步骤如下详述。

在对电网扰动状态下的机电转子稳定控制中，B代表电机气隙磁密，顺着x与y轴位置上分量，可以用式（1）表述为：

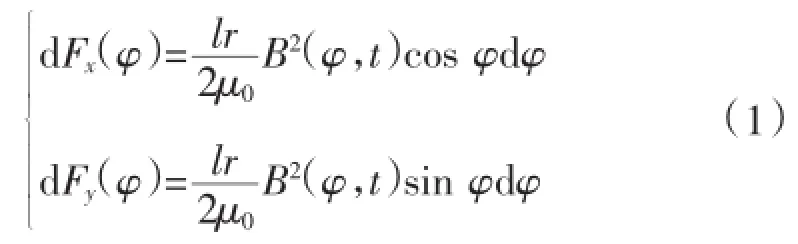
在上式中，由l代表电机定子铁心长度，可以表述为由r代表的外径。

在对电网扰动状态下的机电转子稳定控制中，当转子出现偏移时，其矢量可以表述为：

在上式中，由x、y表述为电涡流位移传感器，且各测得的转子沿x、y方向的偏心位移。

在对电网扰动状态下的机电转子稳定控制中，机电转子偏心位移的方向即偏心位移角度能够表述为：

依据上式可以得出，对机电转子的发电机有功、无功的解耦控制方程，可以用下式表述为：

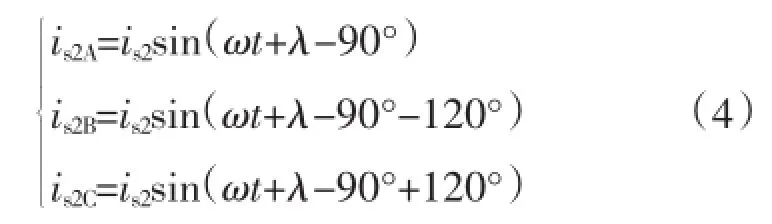
2 控制过程的优化

在对电网扰动状态下的机电转子稳定控制过程中，依据电网在扰动状态下的框架结构，引入FLOYD算法，计算并得到发电机频率特征函数的变化规律，在此基础上对电网系统稳态时和电网扰动状态下机电波到达后发电机频率的特征进行有效的区分。

2.1 电网扰动状态下的发电机频率规律分析

在电网正常运行的状态下，机电设备频率较为稳定，只是会因为负荷而形成频率在50 Hz范围内波动，周期较短。在电网扰动状态下，当机电信号到达后，因为受到长时间不平稳功率的影响，会形成加速或者减速情况，会促使频率在一定时间内出现单调上升和下滑的情况，且周期性较强。在电网稳态时，机电波出现较短周期的波动性，与在电网扰动状态下，当机电到达后周期性较强的单调性区别较为明显。

在对电网扰动状态下的机电转子稳定控制过程中，引入FLOYD算法。由CF（i）代表的时间序列，也可以表述为特征函数。用下式计算：

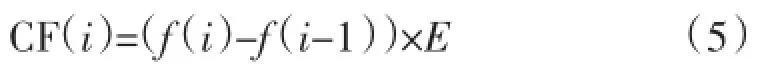
在上式中，由f（i）代表在第i时刻发电机的频率。

在对电网扰动状态下的机电转子稳定控制过程中，依据式（5）可以说明，由CF可以明显的区分电网系统稳态时和电网扰动状态下机电波到达后发电机频率的特征。由W1和W2分别代表发电机频率特征函数范围，利用下式分别定义由L1和L2代表的发电机频率特征函数范围：

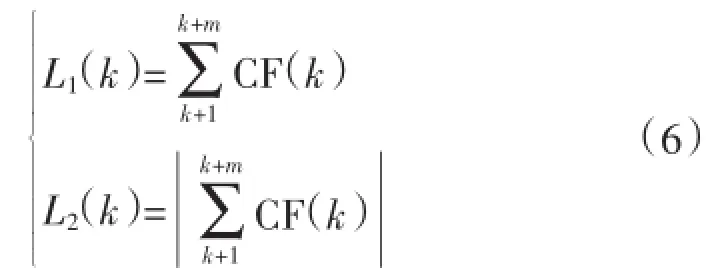
在对机电转子稳定控制过程中，定义由R（κ）代表的第κ点的判别函数，用下式表述为：

当电网的系统处于稳定的状态时，由CF代表的特征函数会形成较短的波动性，因为正负相抵消会促使每个时刻L1的数值较短，而L2的数值也会出现较小的正数，同时也说明了如果电网在稳定的状态下，会在零值范围内迭代。反之，在电网扰动的状态下的数值单调增大或者减小。

依据上述结论可以得到，在电网扰动状态下，机电波到达时刻判断规律如下：

综上所述可以说明，在对电网扰动状态下的机电转子稳定控制中，依据电网在扰动状态下的框架结构，融合于FLOYD算法，计算并得到发电机频率特征函数的变化规律，在此基础上对电网系统稳态时和电网扰动状态下机电波到达后发电机频率的特征进行有效区分的过程，为实现电网扰动状态下的机电转子稳定优化控制奠定了有利的基础。

2.2 机电转子稳定控制过程

在对电网扰动状态下的机电转子稳定优化控制过程中，计算并得到发电机频率特征函数的变化规律后，对电网系统稳态时和电网扰动状态下机电波到达后发电机频率的特征进行有效的区分，并构建一个含有电网系统能力性能控制的李亚普诺夫函数，融合于李亚普诺夫稳定性定理优化设计机电转子状态变量的控制器与高通滤波器，有效完成电网扰动状态下的机电转子稳定控制。具体的步骤如下。

在对电网扰动状态下的机电转子稳定控制过程中，构造的含有电网系统能力性能控制的李亚普诺夫函数用下式表述为：

在上式中，由κE、κθ分别代表电网系统的正常数，因为电网系统能量从始至终为非负，所以由v代表的李亚普诺夫函是正定的。利用下式对v进行计算，可以表述为：

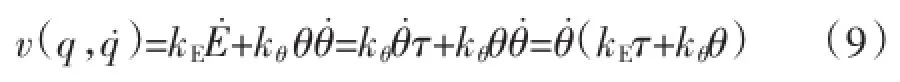
在对电网扰动状态下的机电转子稳定优化控制过程中，融合于李亚普诺夫稳定性判定，设计出机电转子状态变量的控制器，用下式表述为：

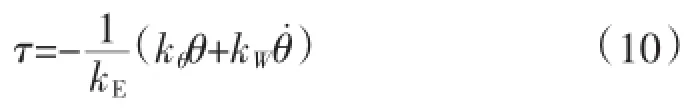
在对电网扰动状态下的机电转子稳定优化控制过程中，依据上式可以求得机电转子闭环控制系统的稳定性。

在对电网扰动状态下的机电转子稳定优化控制过程中，利用高通滤波器估计电网扰动状态下中的速度反馈变量。将控制李亚普诺夫函数重新设计为

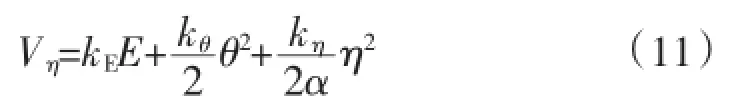
在上式中，由η代表动态滤波器的输出，由α，κη代表正常数。

在对电网扰动状态下的机电转子稳定优化控制过程中，需要设计一个滤波器促使其能够输出一个动态的伪角速度取代真实的机电转子的角速度反馈，因此设计的动态滤波器可以采用下式表述为：

在对电网扰动状态下的机电转子稳定优化控制过程中，利用下式对新的控制李亚普诺夫函数进行计算可以得出：

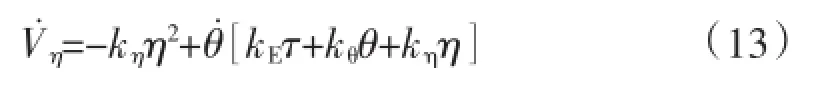
在对电网扰动状态下的机电转子稳定优化控制过程中，要想保证上式得出的由代表的李亚普诺夫函数非负，其控制输入可利 用下式可选为：

在对电网扰动状态下的机电转子稳定优化控制过程中，依据上述结论构建的闭环控制系统在李亚普诺夫意义上是稳定的。

3 实验仿真证明

为了证明电网扰动状态下的机电转子稳定控制方法的有效性，需要进行一次实验。

实验在psim6.0平台上搭建电网扰动状态下的机电转子稳定控制实验平台。利用psim调用C++编译的动态链接库实现电网扰动状态下的机电转子稳定控制实验。实验需要在2 000 r/min满功率时进行，在实际操作的实验中需要收集1 760 r/min满功率时的相应波形。

实验①

在升压变压器高压侧A相串联+10%（2.02 kV）的电压源，通过Dyll变压器后机组进线电压的幅值与相位都存在一定的扰动性，分别采用传统算法与改进算法进行机电转子稳定控制实验，不同算法的波形对比见图1。

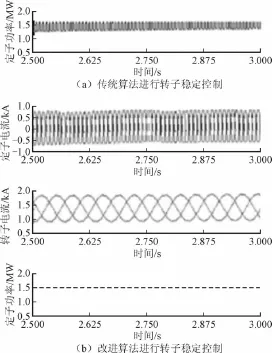
图1 不同算法的机电转子稳定控制对比Fig.1 Different algorithms of mechanical and electrical rotor stability control

从图1中可以看出改进算法进行机电转子稳定控制的稳定性要优于传统算法，这是由于改进算法先依据电网在扰动状态下的框架结构，融合于FLOYD算法，计算并得到发电机频率特征函数的变化规律，在此基础上对电网系统稳态时和电网扰动状态下机电波到达后发电机频率的特征进行有效的区分，因此有效地保障了对机电转子稳定控制的稳定性。

实验②

分别采用传统算法与改进算法进行电网扰动下的机电转子稳定控制实验。将不同算法的控制结果进行对比，用来衡量2种算法的控制效果，对比结果见表1。

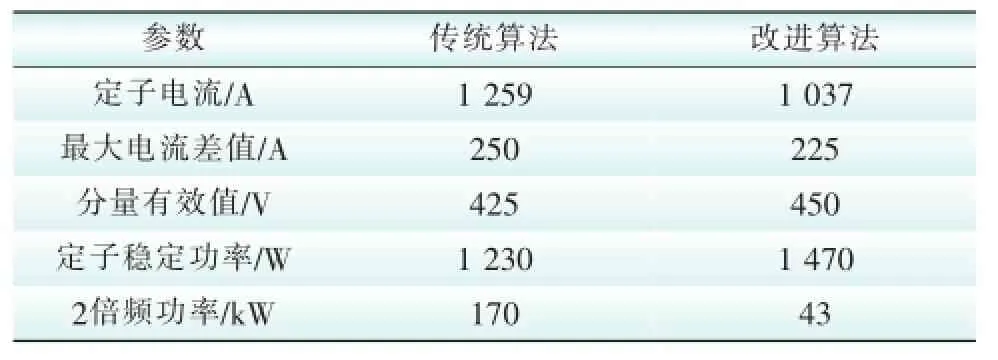
表1 不同算法机电转子控制结果对比Tab.1 The results of different algorithms of mechanical and electrical rotor control

表1可以说明改进算法进行电网扰动下的机电转子稳定控制的精确度要优于传统算法，这是因为使用改进算法计算并得到发电机频率特征函数的变化规律后，对电网系统稳态时和电网扰动状态下机电波到达后发电机频率的特征进行有效的区分，并构建了一个含有电网系统能力性能控制的李亚普诺夫函数，融合于李亚普诺夫稳定性定理优化设计出机电转子状态变量的控制器与高通滤波器，保障了算法控制的精确度。

上述实验可以证明基于改进TORA转子位置反馈算法的电网扰动状态下的机电转子稳定方法精确度高，稳定性强。

4 结语

针对采用当前的算法进行机电转子稳定控制时，转子角行波传输不稳定，造成控制性能差的问题，提出了一种基于改进TORA转子位置反馈算法的电网扰动状态下的机电转子稳定控制方法。该方法依据电网在扰动状态下的框架结构，融合于FLOYD算法，计算并得到发电机频率特征函数的变化规律，在此基础上对电网系统稳态时和电网扰动状态下机电波到达后发电机频率的特征进行有效的区分，并构建了一个含有电网系统能力性能控制的李亚普诺夫函数，融合于李亚普诺夫稳定性定理优化设计出机电转子状态变量的控制器与高通滤波器，有效的完成了电网扰动状态下的机电转子稳定控制。实验仿真证明，基于电网扰动状态下的机电转子稳定控制方法控制精确度高，稳定性强。

[1]邵庆华，邵昱，赵波，等.风速扰动情况下的风电并网电压稳定性研究[J].陕西电力，2013，41（3）：15-17. SHAO Qinghua，SHAO Yu，ZHAO Bo，et al.The wind speed disturbance of wind power grid voltage stability study[J].Journal of Shaanxi electric Power，2013，41（3）：15-17（in Chinese）.

[2]陈恩泽，刘涤尘，廖清芬，等.多重扰动下的跨区电网低频振荡研究[J].电工技术学报，2014（2）：290-296. CHEN Enze，LIU dichen，LIAO Qingfen，et al.Multiple inter-district grid disturbance under the 1ow frequency oscillation research[J].Journal of electrotechnics，2014（2）：290-296（in Chinese）

[3]薛家祥，钟良文，张思章，等.光伏系统中扰动观察法的控制方法研究[J].电气传动，2013，43（3）：40-44. XUE Jiaxiang，ZHONG Liangwen，ZHANG Sizhang，et al. In the photovoltaic system control method of perturbation of observation study[J].electric Drive，2013，43（3）：40-44（in Chinese）.

[4]王长青，张马林，王伟，等.随机扰动情况下绳系卫星状态保持阶段的最优控制[J].空间科学学报，2014，34（6）：881-886. WANG Changqing，ZHANG Malin，WANG wei，et al. The randomized cases tethered satellite state maintenance phase of the optimal control[J].Journal of Space Science，2014，34（6）：881-886（in Chinese）.

[5]李江，李国庆，邹维，等.固定增益与变增益最优励磁控制策略的小扰动稳定域研究[J].电力自动化设备，2014，34（2）：97-100. LI Jiang，LI Guoqing，ZOU Wei，et al.The fixed gain with variable gain the optimal excitation control strategy of small disturbance stability domain research[J].electric Power Automation Equipment，2014，34（2）：97-100.

[6]燕跃豪，毕天姝，杨奇逊.一种基于机电波理论的电网扰动在线定位方法[J].华北电力大学学报：自然科学版，2014，41（1）：1-6.

YAN Yuehao，BI Tianshu，YANG Qixun.A grid disturbance of online positioning method based on the theory of the electromechanical wave[J].Journal of North China electric Power University：Natural Science Edition，2014，41（1）：1-6（in Chinese）.

[7]胡柳，宋平岗.不对称故障下主辅电流控制对双馈电机转子侧变换器的研究[J].科技创新与应用，2013，（8）：13-14. HU Liu，SONG pinggang.Advocate complementary under asymmetric fault current control of doubly-fed motor rotor side converter study[J].Science and Technology Innovation and Application，2013（8）：13-14（in Chinese）.

[8]唐欣，李建霖，滕本科.提高扰动下VSC-HVDC供电电压质量的逆变站控制方法[J].电工技术学报，2013，28（9）：112-119. TANG Xin，LI Jianlin，TENG Benke.Improve the quality of disturbance of VSC-HVDC power supply voltage of inverter station control method[J].Journal of electrotechnics，2013，28（9）：112-119（in Chinese）.

[9]刘巨，孙海顺，文劲宇，等.交流互联电网中大扰动对联络线的冲击特性分析方法[J].电力系统自动化，2013，37（21）：17-22. LIU Ju，SUN Haishun，WEN Jinyu，et al.Ac interconnected power grid cuhk disturbance impact characteristics of 1ink analysis method[J].Automation of electric Power Systems，2013，37（21）：17-22（in Chinese）.

[10]付永新，张永明，张仁杰.电网模拟装置谐波控制器仿真研究[J].计算机仿真，2014，31（7）：140-143. FU Yongxin，ZHANG Yongming，ZHANG Renjie.Power grid harmonic controller simulator simulation[J].Computer Simulation，2014，31（7）：140-143.

（编辑 徐花荣）

Research on Mechanical and Electrical Rotor Stability Control Method under Grid Disturbances

PENG Qiuhong1，ZHOU Xin2
（1.Department of Automation and Information Engineering，Pingdingshan Industrial College of Technology，Pingdingshan 467000，Henan，China；2.School of Network Education，Pingdingshan Industrial College of Technology，Pingdingshan 467000，Henan，China）

In the process of studying the mechanical and electrical rotor stability under the power grid disturbance，if the current method is used for the mechanical and electrical rotor stability，the rotor angle traveling wave transmission is not stable and the control performance is poor.This paper proposes a new method for the mechanical and electrical rotor stability control based on the improved TORA rotor position feedback. This method，based on the unique frame structure of the power gird under disturbances and fusion of the FLOYD algorithm，calculates and obtains the change 1aw of the mechanical and electrical equipment frequency characteristic function.On the basis，effective distinguishing of the electrical and mechanical frequency characteristic upon arrival of the mechanical and electrical wave under both steady power grid conditions and grid disturbances is realized， and also the electrical and mechanical stability control under power grid disturbances is completed.Experiments show that the method is of high control precision and strong stability.

2014-04-08。

彭秋红（1966），女，工程硕士，副教授，主要研究方向为矿山机电技术；

周 昕（1973），男，工程硕士，讲师，主要研究领域为计算机网络技术。

1674-3814（2015）08-0055-04

TM131

A

KEY W0RDS：high-pass filter；the controller；FLOYD algorithm