一类半线性微分方程振动准则的注记

康永强

(广东顺德职业技术学院，广东佛山528300)

1 提出问题

本文在 －1＜p0≤p(t)≤0的情形下，考虑二阶中立型时滞拟线性微分方程

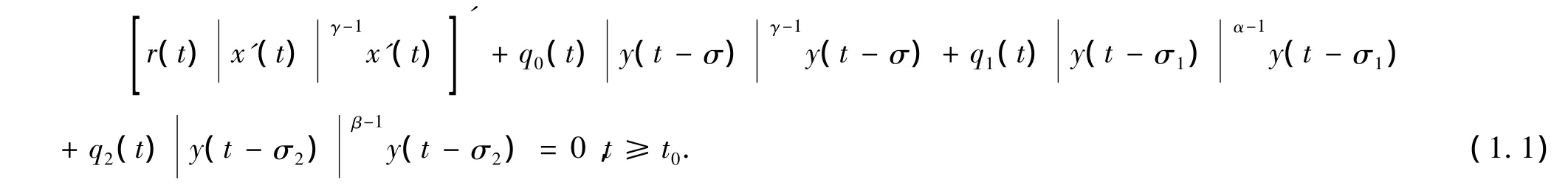
其中，x(t)=y(t)+p(t)y(t－ τ).

首先，有以下假设:

(A1)τ，σ，σ1，σ2是非负的常数，α，β，γ 是正的常数，σ ≥ σ1，σ ≥ σ2且0 ＜ α ＜ γ ＜ β;(A2)q0，q1，q2∈ C(［t0，∞)，R+)，R+= ［0，∞);

(A3)r∈ C(［t0，∞)，(0，∞ )) ，p∈C(［t0，∞)，R)且 －1 ＜ p0≤p(t)≤0，p0是常数.

函数 y(t)∈ C(［Ty，∞)，R)，Ty≥t0，是方程(1.1)的解，如果p(t)|x'(t)|α－1x'(t)∈C1(Ty，∞)且满足方程(1.1)，我们主要考虑方程(1.1)的非平凡解y(t)，即sup{|y(t)|:t≥T}＞0，T≥Ty.如果它有任意大的零点，称之为振动的;否则，称之为非振动的.如果方程(1.1)的所有非平凡解都是振动的，方程(1.1)称为振动的.

当时 p(t)≡0，q1(t)≡0，q2(t)≡0，σ =0 时，方程(1.1)转化为半线性微分方程

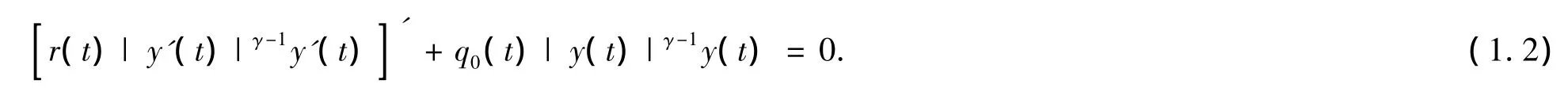
可参见 Elbert［3］，Li和 Yeh［4］.

当 q0(t)≡0，r(t)≡1，σ = σ1= σ2时，方程(1.1)转化为

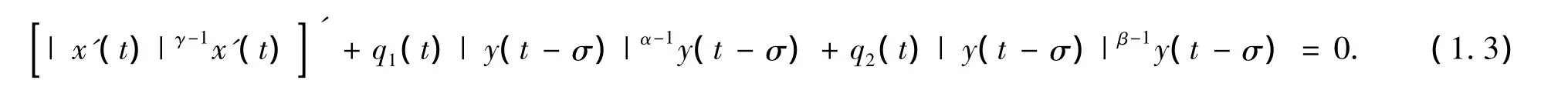
由Xu和Liu［9］得到如下结果.

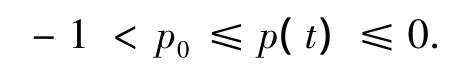
则方程(1.3)是振动的.且

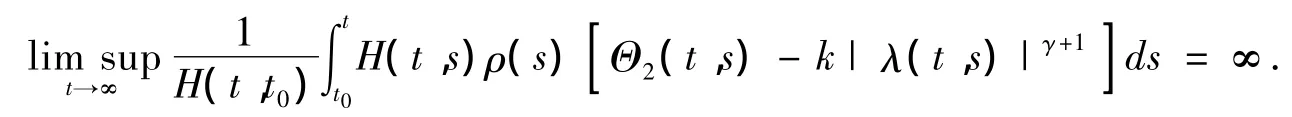
本文受 Wang［7］，Wang 和 Yang［8］，Xu 和 Liu［9］以及 Liu［10］等的启发，将文献［9］的结果推广至(1.1)，修正了Xu和Liu［9］其中的一些错误.

2 二阶中立型时滞拟线性微分方程的振动准则

本文在 －1＜p0≤p(t)≤0的情形下，建立方程(1.1)的新的振动准则.

为了方便表达，作出如下标记:

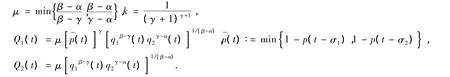
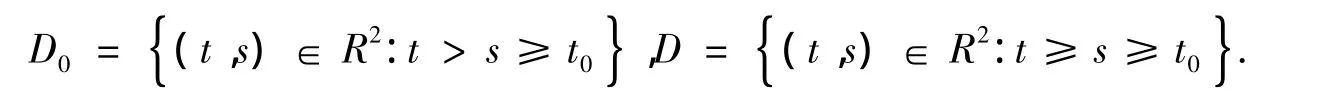
(H1)H(t，t)=0，t≥ t0，H(t，s)＞ 0，(t，s)∈ D0;

(H2)H关于第二个变量有连续和非正的偏导数，满足

对于给定的函数 h ∈ C(D，R)，ρ∈ C1(［t0，∞)，R+)和 η ∈ C1(［t0，∞)，R)，记

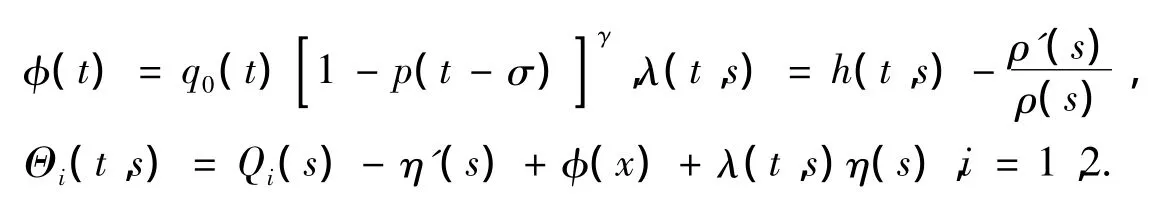
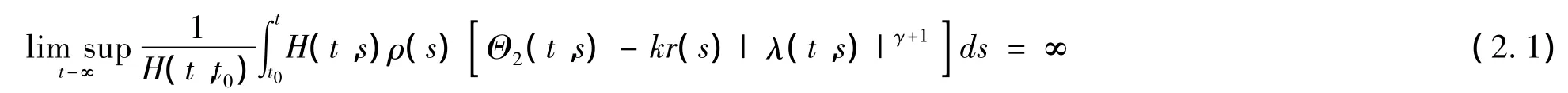
满足，则方程(1.1)的解或者是振动的，或者当t→∞ 时趋于0.

证明 假定y(t)是方程(1.1)的非振动的解，不失一般性，假定y(t)≠0，t≥t0.不妨设存在t1＞t0，使得

成立，类似与文献［11］中引理1(1)的证明.根据文献［11］引理1(2)和文献［10］，对某个T0≥t1+τ+σ，有x'(t)＞ 0且x″(t)＜ 0，但x(t)＞ 0或x(t)＜ 0，t≥T0－ τ － σ.

(i)当x(t)＞0时，注意到y(t)≥x(t)，当t≥T0时，有

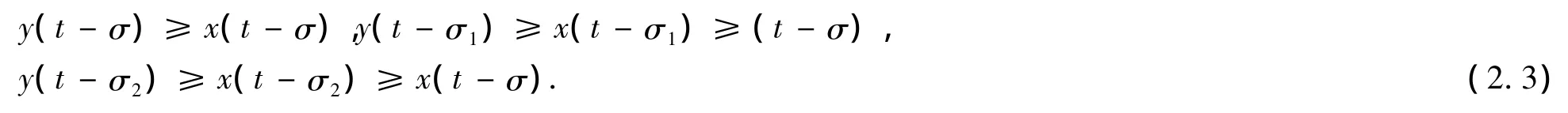
由方程(1.1)，可得

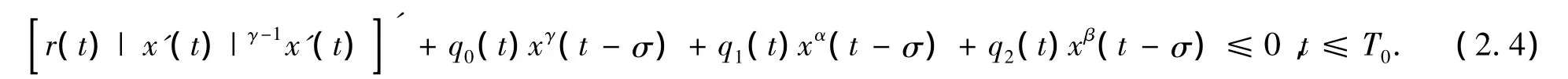
定义ω(t)，

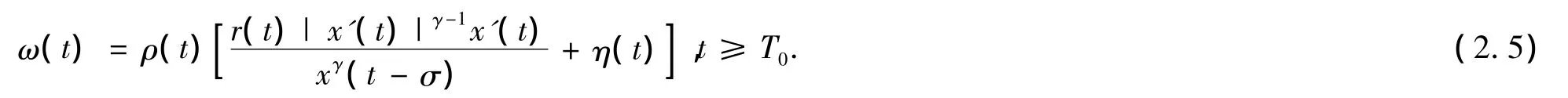
对(2.5)微分，有

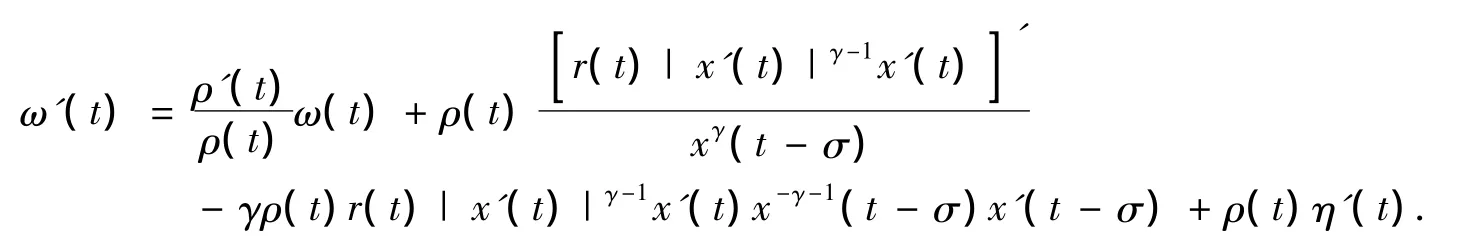
由(2.4)和x'(t)＜ x'(t－ σ)，可得

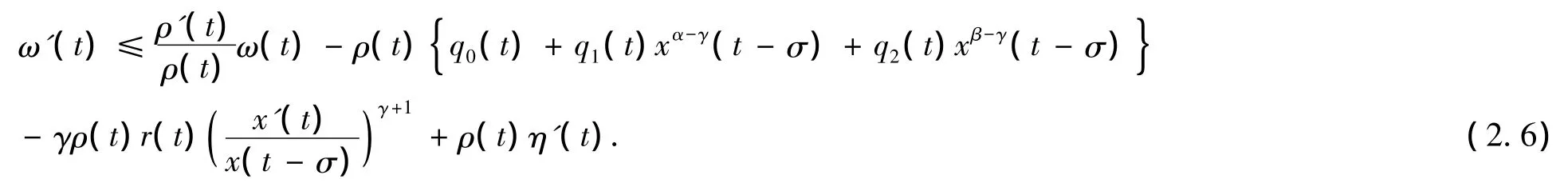
由 Hardy［16］，定理 61，可得

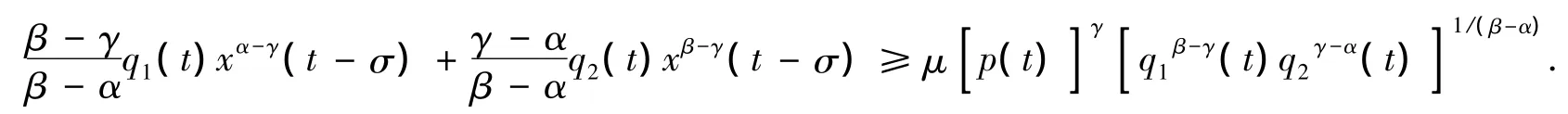
于是

结合(2.6)和(2.7)，当 t≥ T0时，有

将(2.8)用 s代换 t，用 H(t，s)相乘，并在［T，t］上积分，根据(H2)，对所有的 t≥ T ≥ T0，有

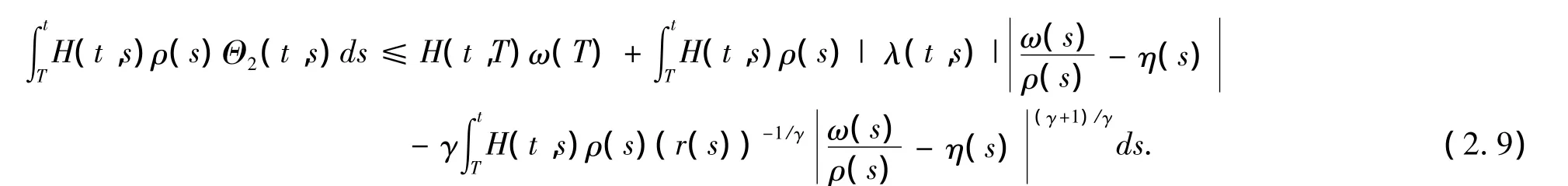
现令

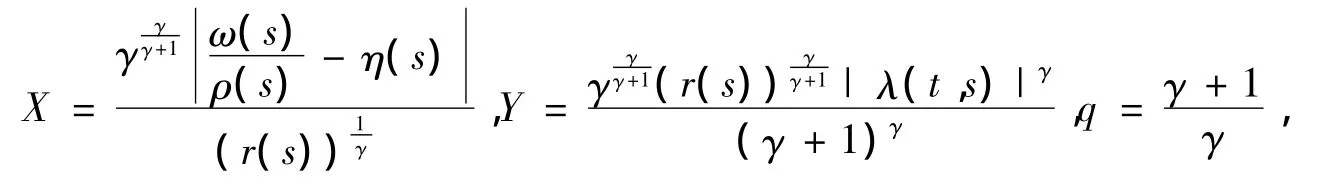
根据文献［16］，则有

将(2.10)代入(2.9)，得到

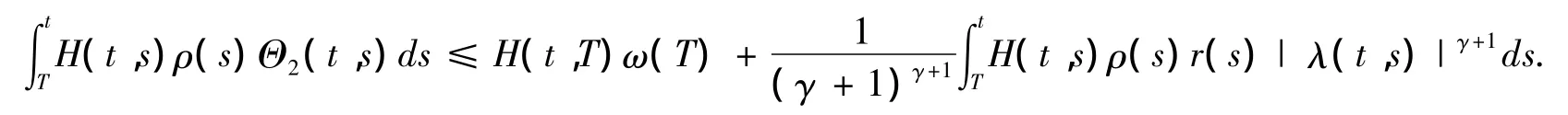
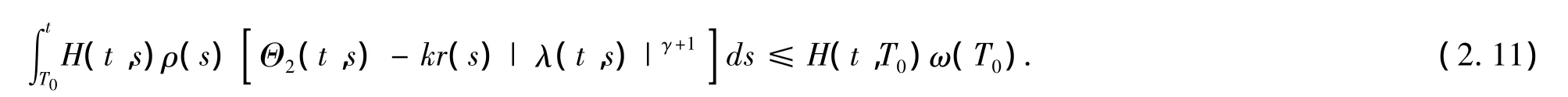
因此，根据(H2)，得到

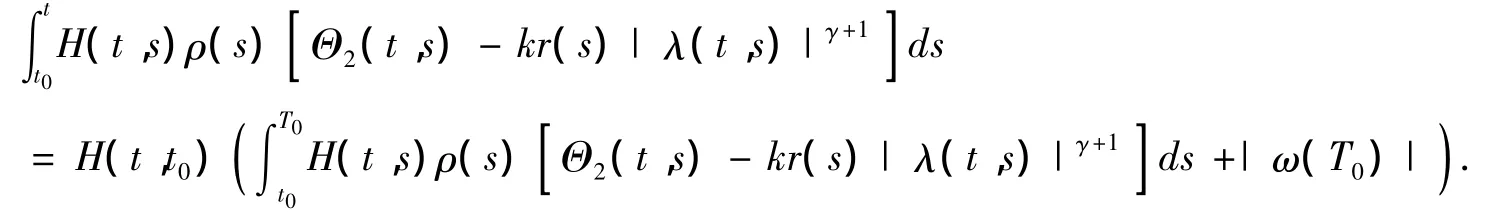
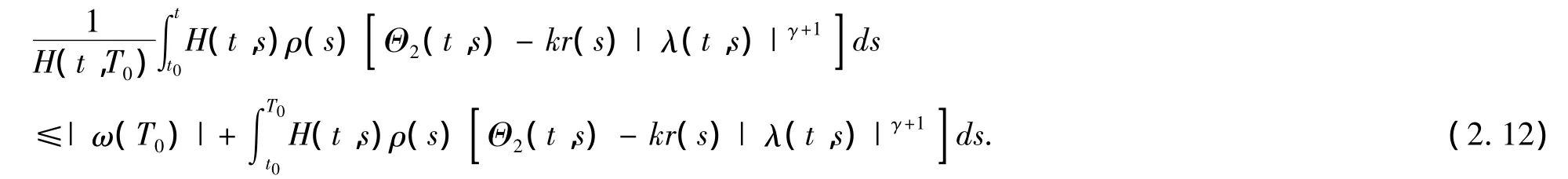
(2.12)在t→∞ 时的上极限的结果与条件(2.1)矛盾，即y(t)是振动的.

(ii)当x(t)＜0时，由文献［10］的结论可知，当t→∞ 时，y(t)趋于0.

由(i)和(ii)，定理2.1得证.

且有

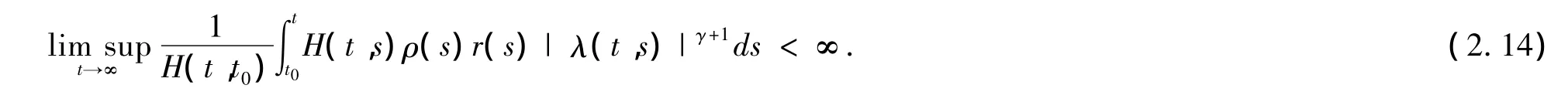
存在 φ ∈ C(［t0，∞)，R)，使得

且对所有的T≥t0，有

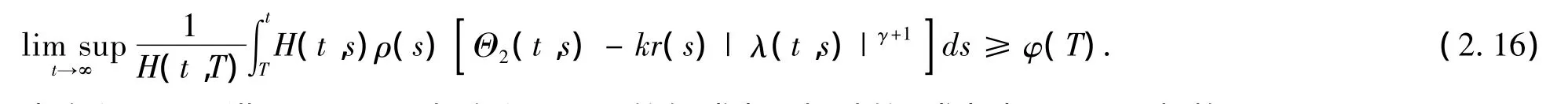
当方程(1.1)满足(2.15)时，方程(1.1)的解或者是振动的，或者当t→∞ 时，趋于0.

证明 定理2.2的证明过程和定理2.1的情形类似，有(2.9)和(2.11)成立.因此，由(2.11)，对于所有的t＞ T≥T0，有

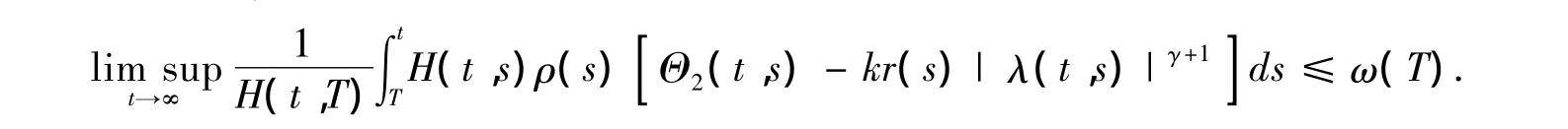
同时，根据(2.16)，则有

定义

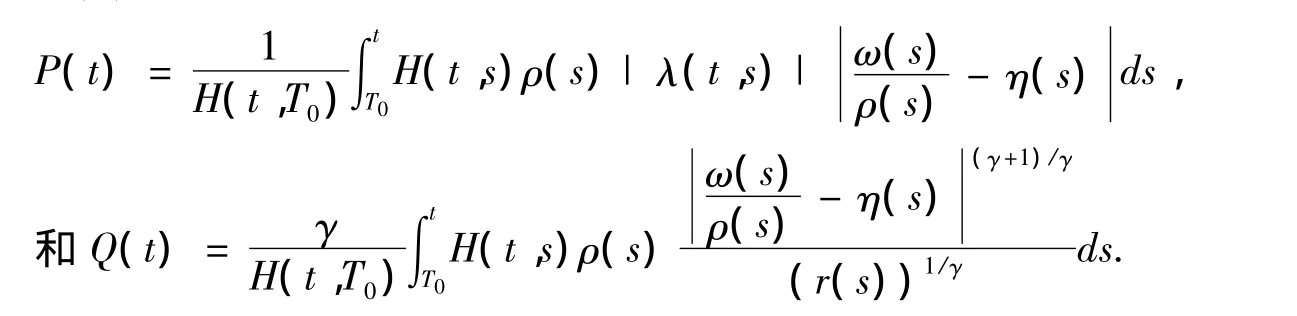
则根据(2.11)和(2.17)，可知

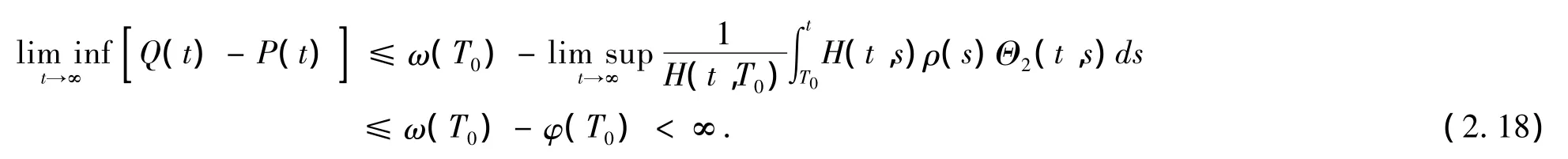
现在，我们断定有下式成立

否则，假定(2.19)相反的情形

根据(2.13)，存在一个正的常数k1，使得

令k2是任意常数，从(2.20)可知，存在T1≥T0，使得

而且

根据(2.21)，存在一个 T2≥ T1，使得 H(t，T1)/H(t，T0)≥ k1，对任意 t≥ T2，说明 Q(t)≥ k2y，即

接下来，观察(2.18)，可以确定一个在［t0，∞)的数列，满足

即存在常数M，使得

对任意大的n∈N，由(2.23)确定

另外，由(2.24)表明

因此，由(2.24)和(2.26)，得出不等式

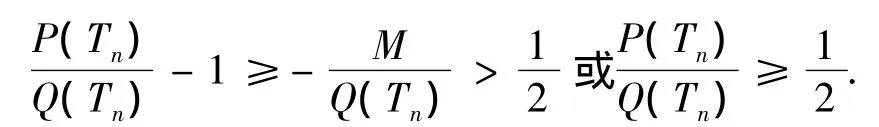
对任意大n∈N，观察上式从及(2.26)，有

这样，由(2.27)，则

与(2.15)矛盾，因此(2.21)成立.由(2.19)和(2.21)得到

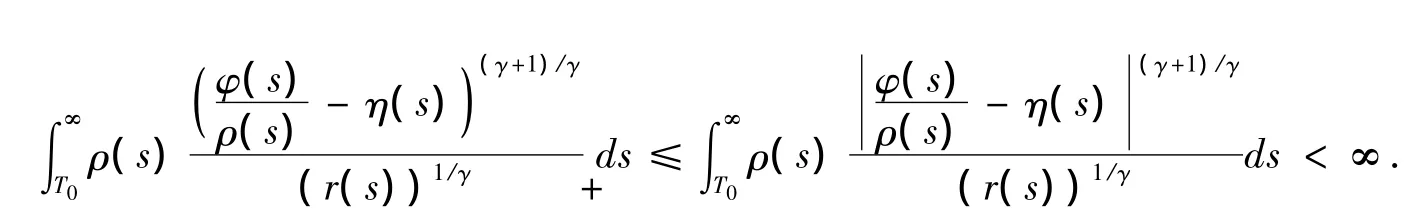
与(2.15)矛盾.则定理2.2 得证.

以下定理的证明都类似于定理2.1和定理2.2，故略去.

存在 φ∈C (［t0，∞)，R )，使得(2.16)成立，且对所有的T≥t0，有

当方程(1.1)满足(2.28)时，方程(1.1)的解或者是振动的，或者是当时t→∞，趋于0.

当方程(1.1)满足(2.29)时，方程(1.1)的解或者是振动的，或者是当t→∞ 时，趋于0.而且，假设φ∈C(［t0，∞)R)，且(2.16)和(2.28)成立.

3 结论

当 －1 ＜ p0≤p(t)≤0时，定理2.1、定理2.2、定理2.3和定理2.4修正了Xu和Liu［9］中相应的结果.具体地，由于Xu和Liu［9］引用的文献［11］中引理1(2)有误［10］，得到方程(1.3)是振动的;而我们的结论是:方程(1.1)的解或者是振动的，或者是当t→∞ 时，趋于0.

［1］C.A.Swanson.Comparison and Oscillation Theory of Linear Differential Equations［M］.New York:Academic Press，1968.

［2］燕居让.常微分方程的振动理论［M］.太原:山西教育出版社，1992.

［3］A.Elbert.A half－ linear second order differential equation，Colloq［J］.Math.Soc.Janos Bolyai:Qualitative Theory of Differential Equations，Szeged，1979:153 －180.

［4］H.J.Li，CC.Yeh.Sturmian comparison theorem for half－ linear second－order differential equations［M］.Proc.Royal Soc.Edinburgh，1995，125A:1193 －1204.

［5］J.V.Manojlovi’c.Oscillation criteria for second－order half－ linear differential equations［J］.Math.Comput.Modelling，1999(30):109－119.

［6］Ch.G.Philos.Oscillation theorems for linear differential equations of second order［J］.Arch.Math.(Basel)，1989(53):482－492.

［7］Q.R.Wang.Oscillation and asymptotics for second－order half－ linear differential equations［J］.Appl.Math.Comput，2001(2):253－266.

［8］Q.R.Wang，Q.Yang.Interval criteria for oscillation of second－order half－ linear differential equations［J］.J.Math.Anal.Appl，2004，291(1):224 －236.

［9］XU Zhiting，LIU Xiuxiang.Philos－ type oscillation criteria for Emden－Fowler neutral delay differential equations［J］.J.Comput.Appl.Math.，2007(2):1116 －1126.