数学软件Mathematica在高等数学中的应用
2015-12-29孔祥强
孔祥强
(菏泽学院 数学系,山东 菏泽 274015)
Mathematica软件是一款集符号计算、数值运算和绘图功能于一身的数学类软件.其主要特点有:(1)入门简单,命令多样,易操作;(2)软件的编程语言简单,便于编程;(3)强大的绘图功能,可绘制平面图形和空间图形;(4)可与MATLAB软件、Maple软件之间互相调用[1].高等数学是高等院校学生重要的基础课程,对学生专业课的学习有很好的辅助作用,而高等数学的内容比较抽象,概念较难理解,计算较繁琐,使得部分同学不知如何学这门课.为了提高学习的积极性,调动起学习的主动性,在大学课堂里引入数学软件是一种非常好的教学模式.通过Mathematica软件,将抽象的内容以图形的方式展现出来,方便观察或验证一些规律和结论[2].Mathematica软件学生版的出现,学生们使用起来会更加方便[3].
文章通过案例,说明了软件在函数极值、立体体积、中值定理和二次型中的具体应用.
1 Mathematica软件在求函数极值中的应用
一元函数求极值,主要的是利用一阶导数和二阶导数的知识,一般计算量不大.而二元函数求极值,用到二阶偏导数,计算量大.利用软件,可快速求出驻点,判断在二阶偏导处的值,得出极值点,通过作图,直观理解所求的极值点在图形上的位置,加深对多元函数极值点的理解.
案例1 求s(x,y)=x3-2y3+6x2+3y2+9x-9的极值,并通过作图对结果进行说明.源程序如下

求出驻点的坐标为(-3,0),(-3,1),(-1,0),(-1,1).


求出在驻点处的AC-B2的值、A的值、s(x,y)的值为
{-36,-6,-9},{36,-6,-8},{36,6,-13},{-36,6,-12}
在点(-3,0)处,AC-B2=-36<0,故不是极值点;
在点(-3,1)处,AC-B2=36>0,故是极值点,又 A=-6<0,是极大值点;
在点(-1,0)处,AC-B2=36>0,故是极值点,又 A=6>0,是极小值点;
在点(-1,1)处,AC-B2=-36<0,故不是极值点.
因此s(x,y)在(-3,1)处取得极大值,为-8;在(-1,0)处取得极小值,为-13.
作出函数s(x,y)的图形

从图1明显得出,函数有两个极值点.在Mathematica窗口下,用鼠标点击图形,任意改变视角,可方便观察两个极值点的位置,比较极值点和周围点所对应的函数值,深刻理解极值的概念.
除了上面的方法,还可用等高线研究s(x,y)的极值.调用ContourPlot命令,

图1 s(x,y)=x3-2y3+6x2+3y2+9x-9图形


图2 函数s(x,y)的等高线图
从上图看出,s(x,y)有两个极值点,分别为(-3,1)和(-1,0),验证了所求的结论是正确的.
2 Mathematica软件在求空间立体体积中的应用
要求空间立体的体积,首先应作出立体图形,再选择用直角坐标、极坐标、柱面坐标或球面坐标.利用软件,可方便作图.
案例2 求由平面x=0,y=0,z=0,x+y=-1及曲面z=8-3x2-3y2所围成的立体Ω的体积,并作图.
由于Ω为空间立体,首先应该清楚Ω的形状和在坐标面上的投影,然后用二重积分来求Ω的体积.调用Mathematica软件的ParametricPlot3D命令,作出三个坐标面x-0,y=0,z=0、柱面x+y=-1、抛物面z=8-3x2-3y2的图形.程序如下


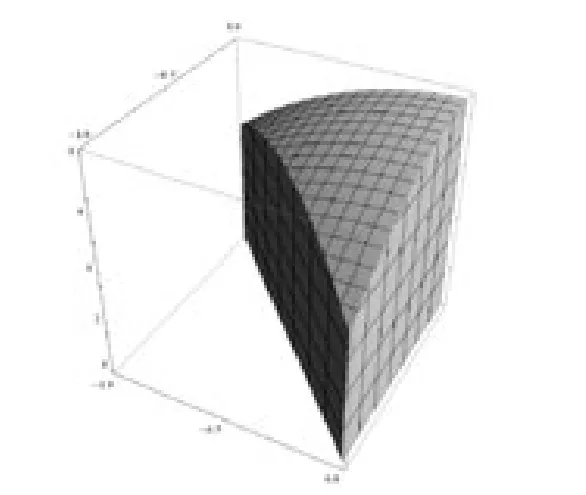
图3 立体Ω的图形
Ω在坐标面x=0上的投影为直角三角形,见图4.

图4 立体Ω在xoy面上的投影
分析清楚Ω的空间形状和在坐标面上的投影后,利用Integrate命令,就可求出Ω的体积,

3 Mathematica软件在中值定理中的应用
高等数学中的泰勒定理非常抽象,较难掌握.麦克劳林公式作为泰勒定理的特例[4],一般考察函数的麦克劳林展式.
若函数f(x)在点x0=0的某领域内U(x0)内有n+1阶导数,f(x)在x0=0处的n阶麦克劳林展式为

调用Series命令,得展开式.

调用Plot命令,作出图形.
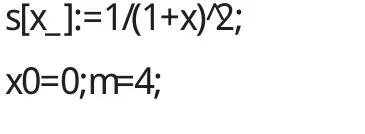


图5 f(x)=1/(1+x)2的各阶麦克劳林展开式
在Mathematica窗口下,可动态观察各阶曲线与函数f(x)=1/(1+x)2的逼近程度,阶数越高,和函数的逼近程度越好,误差很小.
4 Mathematica软件在二次型中的应用
二次型是大学数学中的重要内容,其中化二次型为标准形是重要的题型.这类题目的特点是用到的知识点多,计算繁琐.利用Mathematica软件和多媒体技术,作起来非常轻松.
案例4 用正交变换的方法化二次型f(x1,x2,x3)=x12-2x22-2x32-4x1x2+4x1x3+8x2x3为标准形,并指出f(x1,x2,x3)=1表示何种二次曲面[5].
针对这种题型,一般先求出二次型所对应的矩阵A,再求A的所有特征值和属于每一个特征值的特征向量,然后用Schmidt正交化过程[6],将特征向量正交化、单位化,从而得到正交矩阵P,正交变换为x=Py,最终得到二次型的标准形.这个计算过程非常复杂,稍有不慎就会出错.引入Mathematica软件,调用Eigenvalues和Eigenvectors命令分别得特征值和特征向量,用Orthogonalize命令进行Schmidt正交化过程.


故二次型的标准形为f(x1,x2,x3)=-7y12+2y22+2y32,f(x1,x2,x3)=1即-7y12+2y22+2y32=1,表示单叶旋转双曲面.
通过Mathematica软件中几个简单的命令,避免了冗长繁杂的计算,快速、高效的解决了问题.数学软件与多媒体技术结合的教学模式,能增加学生学习的趣味性,更能深刻的理解所学的知识,掌握解题的整体框架结构,全面把握问题.
5 结语
在高等数学的教学过程中引入Mathematica软件,加强了对数学概念的直观理解,真正的学懂数学.华罗庚先生说:“数无形时少直觉,形无数时难入微”,可见数形结合的重要性,而软件就是通过图形深刻揭示表达式中隐含的数学联系.软件的演示功能,活跃了课堂气氛,增进了师生的交流,促进了学生的积极思考,激发了学习的主动性.
〔1〕李尚志,陈发来.数学实验[M].北京:高等教育出版社,2004.10-186.
〔2〕李士恒.Mathematica在数学实验中的应用[J].中央民族大学学报(自然科学版),2014,23(3):14-17.
〔3〕许和乾,杜炜.基于数学软件Mathematica的高等数学教学实践[J].合肥师范学院学报,2014,32(3):76-78.
〔4〕李伟.高等数学[M].北京:高等教育出版社,2011.131-160.
〔5〕徐仲,陆全,张凯院,等.高等代数考研教案[M].西安:西北工业大学出版社,2009.200-271.
〔6〕王萼芳,石生明.高等代数[M].北京:高等教育出版社,2013.355-393.
〔7〕马千里.Mathematica软件在微积分教学中的应用[J].陕西师范大学学报(自然科学版),2009,37(Sup):135-136.
