基于高温铸坯蠕变规律的连铸坯幂函数连续矫直法

基于高温铸坯蠕变规律的连铸坯幂函数连续矫直法

任廷志韩培培

燕山大学国家冷轧板带装备及工艺工程技术研究中心，秦皇岛，066004

摘要：根据国内外近年来高温铸坯蠕变规律研究成果，建立了矫直区内铸坯变形的数学模型，由此推导出矫直区内铸坯连续矫直曲线方程。辊列按照该矫直曲线布置，完全满足高温铸坯蠕变变形规律。矫直区内的铸坯在中间段实现了等应变速率变化规律，起始段和末尾段实现幂函数形式的应变速率变化规律。利用实验辊列装置对该矫直曲线进行了实验研究，采用一种常温完全蠕变锡铋合金代替高温铸坯，对实验铸坯所受矫直力与铸坯应变进行测量，所测结果与理论计算结果相吻合。

关键词：连铸；连续矫直；应变；应变速率

中图分类号：TF777.1

收稿日期：2015-06-08

基金项目：国家科技支撑计划资助项目(2011BAF15B01)

作者简介：任廷志，男，1960年生。燕山大学国家冷轧板带装备及工艺工程技术研究中心教授、博士研究生导师。主要研究方向为连铸机设计理论及装备、连铸过程数值模拟、机械设计及智能化。发表论文50余篇。韩培培，男，1986年生。燕山大学国家冷轧板带装备及工艺工程技术研究中心博士研究生。

Power Function Continuous Straightening Method for Casting Strand Based on Creep

Behavior of Metal at Elevated Temperature

Ren TingzhiHan Peipei

National Engineering Research Center for Equipment and Technology of Cold Strip Rolling,

Yanshan University,Qinhuangdao,Hebei,066004

Abstract:According to the recent study results of the creep behavior of metal at elevated temperature, a mathematical model of the strand deformation was developed and a continuous straightening curve was derived. The rollers were arranged along the curve, making the roll apron fully accommodate the creep behavior of metal at elevated temperature. Then the strand deformation features were presented. During the straightening process, the strain rates of the strand remained constant in the middle part of the straightening zone; while at the start and the end parts of the straightening zone, the strain rates of the strand were in the form of power function. Finally, an experimental research on the curve was carried out using a pilot roll supporting system. And the experimental material was a kind of Sn-Bi alloy to substitute the steel at elevated temperature. During the experimental process, the bending forces acting on the strand and the strains of the strand were measured. And the measurement results are in good agreement with the theoretical calculations.

Key words: continuous casting; continuous straightening; strain; strain rate

0引言

随着连铸坯带液芯弯曲与矫直技术的诞生和发展，铸坯弯曲与矫直造成坯壳凝固前沿的内裂成为影响铸坯内部质量的关键因素。当坯壳固液交界面处的应变超过临界应变时，裂纹将会产生，而在凝固前沿，临界应变不是一个定值，它与应变速率有关，降低应变速率可以提高临界应变值[1-4]。因此，准确计算铸坯在弯矫区的应变速率，确定合理的弯矫区曲线对于连铸机设计和保证产品质量具有十分重要的意义。

在连铸技术领域，学者们围绕连铸坯弯曲和矫直已进行了大量的理论和应用研究。自Olsson[5]提出逐步弯曲矫直的思想以来，连铸机弯矫区辊列设计理论可分为两个发展阶段。第一个阶段是从弯矫区辊列布置曲线设计出发，辊列按照曲率逐步变化或逐渐变化的曲线布置。如Bungeroth等[6]提出多段圆弧相连接构成弯矫区辊列布置曲线的方法，使总应变分散到圆弧连接点上。该方法也被称为多点矫直法，首次应用于胡金根公司的超低头连铸机上。Schneckenburger[7]提出用悬链线、双曲线、抛物线中的任意一种作为铸机辊列布置曲线，Bondanelli[8]也提出了抛物线和双曲线的辊列布置形式。第二个阶段的设计方法基于特定的力学模型从铸坯应变速率角度出发设计弯矫区辊列曲线。奥钢联Voest-Alpine弯曲法中，铸坯受4对矫直辊作用完成弯曲或矫直[9]，林茨工厂的二号板坯连铸机辊列设计采用的就是这种方法。康卡斯特连续矫直法中，铸坯同样是在4对辊子的作用下完成矫直[10]。该方法的首次应用是在法国Sollac厂的1号板坯连铸机上。基于铸坯的受力模型对弯矫区辊列进行设计是铸坯矫直理论发展的一个重要进步。

然而康卡斯特连续矫直法未考虑起始段和末尾段的线性弯矩对铸坯变形的影响；奥钢联连续矫直法虽然考虑了起始段和末尾段的线性弯矩对铸坯变形的影响，但其矫直曲线也不能完全满足铸坯的蠕变规律，使辊列布置曲线与铸坯变形曲线存在一定偏差。这种偏差将对整个矫直区内的铸坯受力与变形产生影响，使铸坯产生不必要的变形，铸坯坯壳未按照连续矫直曲线的规律发生变形，不能实现真正意义上的坯壳等应变速率变形，这会对铸坯质量产生不利的影响。本文基于国内外近年来对高温铸坯蠕变规律的研究成果，建立矫直区内铸坯变形的数学模型，由此推导矫直区内铸坯连续矫直曲线方程。利用实验辊列装置对该矫直曲线进行实验研究，采用一种常温完全蠕变锡铋合金代替高温铸坯，对实验铸坯所受矫直力与铸坯应变进行测量。

1连续矫直法基本原理

连续矫直法以奥钢联Voest-Alpine弯曲法以及康卡斯特连续矫直法为代表。两种连续矫直法的理论中铸坯在矫直区内的受力模型如图1a所示，铸坯在矫直区只受4对辊子的矫直作用，其他辊子不参与矫直。矫直区弯矩分为3段，如图1b所示：AB段弯矩从零线性变化至某一常量并在BC段保持恒定，该常量在CD段线性变化至零。两种连续矫直法的理论中铸坯坯壳在矫直区BC段按等应变速率规律变化。对于矫直区AB段与CD段，奥钢联Voest-Alpine弯曲法认为铸坯坯壳的应变速率线性变化与弯矩图规律相同[9]，如图1c所示。康卡斯特连续矫直法直接忽略了AB段与CD段铸坯的变形[10]，如图1d所示。奥钢联Voest-Alpine弯曲法与康卡斯特连续矫直法提出的矫直曲线，其中间矫直段的等应变速率矫直满足高温铸坯蠕变规律，而起始段和末尾段的非等应变速率矫直不满足高温铸坯蠕变规律。

图1　连续矫直曲线的特征

理想的连铸坯矫直方法应根据图1a所示的力学模型，根据高温铸坯的本构方程计算整个矫直区内铸坯变形曲线，并按照铸坯变形曲线进行辊列布置。为了满足这些要求，提出了幂函数连续矫直法。

2幂函数连续矫直法

2.1高温状态下铸坯的本构方程

合适的材料本构方程是研究连铸过程中坯壳变形行为的基础。在高温状态下，铸坯材料发生变形时，应力具有显著的应变速率敏感性，材料符合黏塑性本构模型。很多学者对连铸过程中坯壳材料的本构关系进行了研究，提出了相应的黏塑性本构方程[11-17]。其中，描述材料黏塑性本构关系的Arrhenius定律认为，蠕变变形是一种热激活过程；Norton定律则概括了幂函数形式的材料黏塑性本构方程，这些本构方程在铸坯坯壳变形的计算中得到了应用与验证[18-21]。两种定律的本构方程为

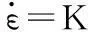
(1)

Kozlowski等[16]用式(1)中的Arrhenius定律描述碳含量w(C)范围为0.005%～1.54%、温度范围为900～1400℃的碳钢的本构关系，其中C′=24 233+49 973w(C)+48 757w2(C)，Qa=49 480R，n=5.331+4.116×10-3T-2.116×10-6T2；El-Bealy等[17]用式(1)中的Norton定律描述温度范围为850℃～TL(TL为液相线温度)的铁碳合金的本构方程，并将其应用于铸坯矫直过程中坯壳应变的计算，其中K=1.215×107(TL-T)-5.932，n=3.313。在矫直过程中坯壳温度在0.7Ts以上(Ts为材料固相线温度)，在这个温度范围内，材料变形符合黏塑性本构模型。本文将式(1)作为研究矫直区内铸坯变形规律的本构方程。

2.2矫直曲线的数学模型

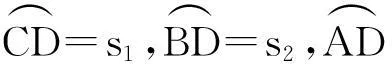
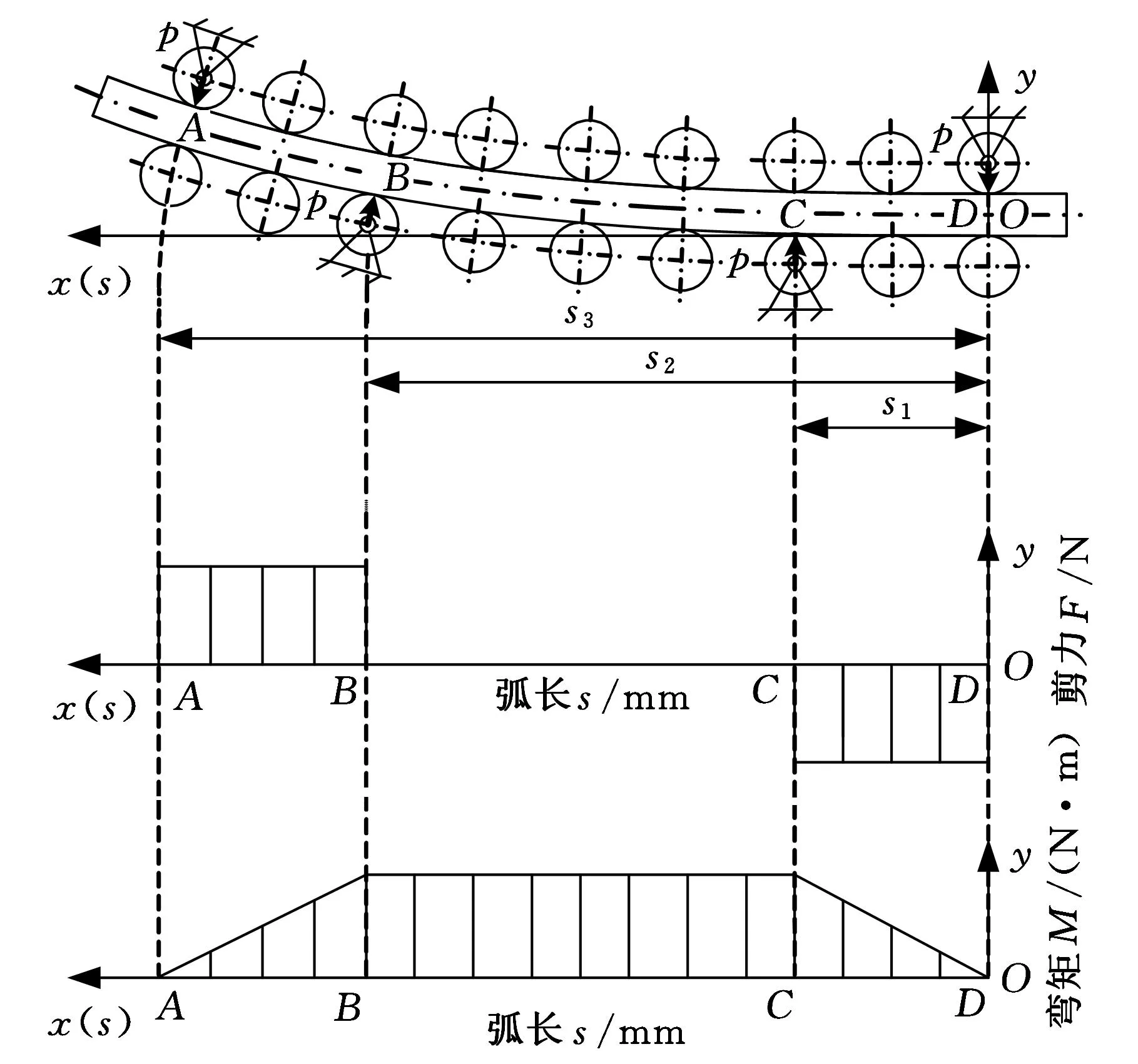
图2　铸坯在矫直区的力学模型

图2中的弯矩图方程为

(2)

令ps1=M0，可得p=M0/s1，代入式(2)可得

(3)

铸坯在矫直过程中，平面假设依然成立[10]。铸坯矫直弯矩M(s)与横截面上应力σh的关系为

M(s)=∫ShσhdS

(4)

式中，S为铸坯横截面的积分面积；h为铸坯横截面上任意一点距中性轴的距离；σh为铸坯横截面上距离中性轴h处的应力。

铸坯横截面上距中性轴h处的坯壳应变ε与铸坯变形曲线在s处的曲率k(s)的关系为

ε=-k(s)h

(5)

式(5)对时间求导可得

(6)

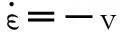
(7)

(8)

Ic=-∫S(-C′(-1/n)/n)exp(-Qa/RT)h1+1/ndS

由于整个矫直区内铸坯温度与坯壳厚度变化均不大，可认为Ic在矫直区是常数。

将式(3)代入式(8)可以得到受力模型中铸坯变形曲线的曲率导数方程：

(9)

对式(9)积分可得在受力模型中铸坯变形曲线的曲率方程：

(10)

在铸机辊列中，A点是矫直区与圆弧区的连接点，因此铸坯在A点曲率应等于铸坯在圆弧区的曲率1/Rm，Rm为铸机半径。将s=s3，k(s)AB=1/Rm代入式(10)可得

(11)

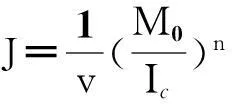
(12)

式(12)代入式(9)得到矫直区内铸坯变形曲线的曲率导数方程:

(13)

式(12)代入式(10)得到矫直区内铸坯变形曲线的曲率方程:

(14)

对式(14)积分得到矫直区内铸坯变形曲线的转角方程:

(15)

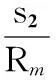
根据微分三角形原理，并用泰勒公式分别展开正弦函数和余弦函数:

(16)

式中，x为矫直曲线在直角坐标系的横坐标；y为矫直曲线在直角坐标系的纵坐标；θ为矫直曲线的转角。

式(15)代入式(16)消去θ，对所得方程进行积分可得直角坐标系下矫直区内铸坯变形曲线关于弧长s的方程。式(15)代入式(16)的一阶泰勒级数消去θ，可得x=s，对所得方程进行积分可得

(17)

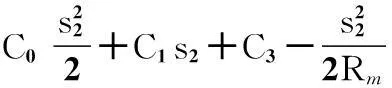
由式(17)可以看出，直角坐标系下矫直区内铸坯变形曲线方程形式为高阶幂函数，矫直区辊列按照铸坯变形曲线进行布置，这种铸坯的矫直方法即为幂函数连续矫直法。

2.3矫直曲线的适用范围

幂函数矫直法的矫直模型中，有4对辊子参与矫直。对于板坯连铸机，矫直区辊列除了矫直功能外还兼具支导铸坯、控制坯壳鼓肚的作用，其辊子的数量大于4对，因此该矫直曲线适用于板坯连铸机的矫直区辊列。对于小方坯或大方坯连铸机，辊列的支导作用通常在矫直段前就完成了，其矫直过程由专门的矫直设备完成。小方坯的矫直设备通常只具有3对辊子，因此该矫直曲线不适用于这种类型的小方坯矫直设备。大方坯的矫直设备通常具有4对辊子，这4对辊子的几何位置可以通过该模型计算得出，以在矫直区实现大方坯的连续矫直，因此该矫直曲线适用于这种类型的大方坯矫直设备。

3实验

实验装置分为圆弧段辊列、矫直段辊列与水平段辊列，矫直段辊列可以根据不同的矫直曲线进行布置，并可对辊子的受力进行测量，试验装置带有4个驱动辊对，可实现不同的拉坯速度，如图3所示。实验装置中，圆弧段半径为1.2m；辊子直径为30mm；实验材料为锡铋合金，其规格为40mm×80mm×1700mm。矫直区共有10对辊子，辊列编号为1～10，其位置根据幂函数连续矫直法的矫直曲线进行布置，矫直曲线长度为sCD=230mm,sBD=790mm,sAD=1010mm，如图4所示。

图3　实验装置

图4　实验装置原理图

实验材料锡铋合金的主要化学成分如下：w(Pb)=42%，w(Bi)=53%，w(Sn)=5%。该材料与高温铸坯具有相似的力学性能，实验铸坯材料力学性能如图5所示。

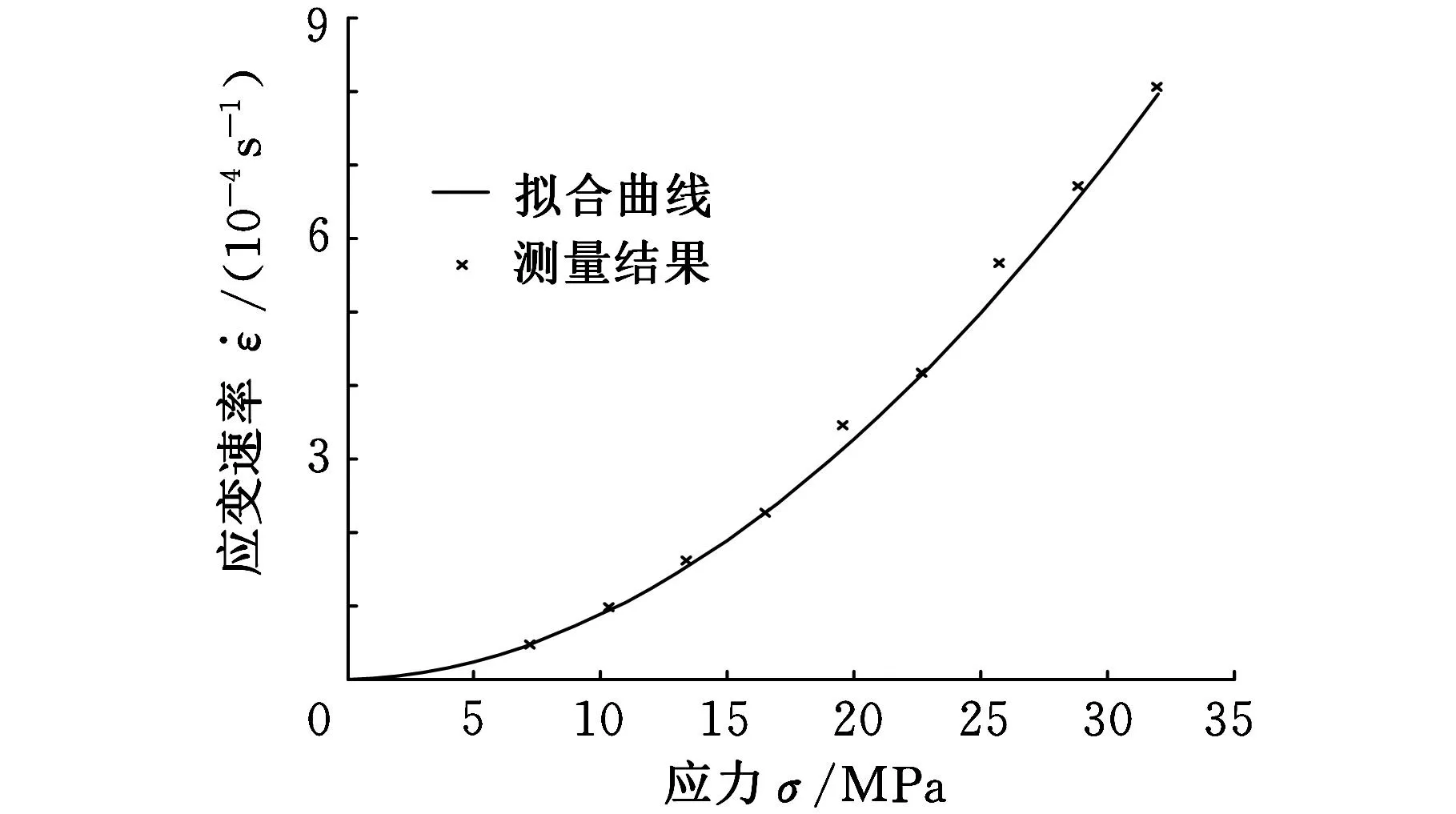
图5　实验材料力学性能

实验测量矫直过程中矫直区辊子受力值以及铸坯上表面的应变。分别以0.12m/min、0.27m/min和0.54m/min的拉坯速度对实验铸坯进行矫直。矫直力的计算值与测量值如表1、表2和表3所示。

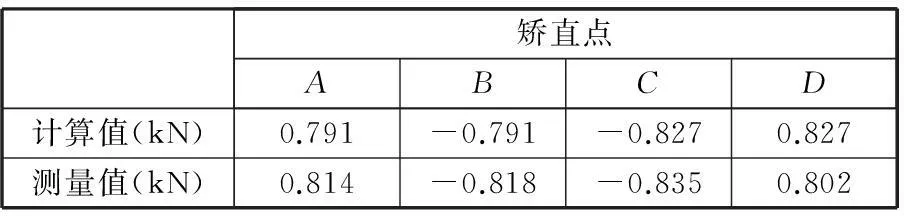
表1　矫直力计算值与测量值( v=0.12m/min)

表2　矫直力计算值与测量值( v=0.27m/min)

表3　矫直力计算值与测量值( v=0.54m/min)

实验铸坯的受力与变形如图6所示，图6中，由上而下依次为受力模型、矫直区辊子受力的测量值与计算值(v=0.54m/min)、矫直区铸坯的剪力图、矫直区铸坯的弯矩图、铸坯表面的应变测量值与计算值、铸坯表面的应变速率。

图6　实验铸坯的受力与变形

由表1、表2和表3可以看出，矫直力的测量结果与计算结果误差在5%以内；铸坯所受矫直力随着拉坯速度的增大而增大。由图6可以看出，辊列按幂函数连续矫直曲线布置，铸坯在矫直区所受矫直力的实测值与理论值吻合得很好，说明实验铸坯在矫直区实现了理论受力模型；铸坯在矫直区应变的实测值与理论值吻合得很好，说明铸坯在矫直区实现了理论变形规律。根据图6的铸坯坯壳表面的应变速率图，铸坯BC段发生等应变速率变形，AB段与CD段铸坯变形的应变速率为幂函数形式。

4结论

(1)根据国内外近年来对高温铸坯蠕变规律研究成果，建立了矫直区内铸坯变形的数学模型，由此得到矫直曲线方程——幂函数连续矫直法。矫直曲线方程的推导过程中以铸坯变形曲线的弧长作为方程的变量，得到的铸坯变形曲线方程能够准确描述矫直区内铸坯的变形。

(2)在幂函数连续矫直法中，矫直区内的铸坯在中间矫直段实现了等应变速率变化规律，起始段和末尾段实现幂函数形式的应变速率变化规律。因此，矫直区辊列按幂函数连续矫直曲线布置能够完全满足高温铸坯蠕变变形规律。

(3)实验材料锡铋合金与高温铸坯具有相似的力学性能，理论计算结果和实验数据相吻合。

参考文献：

[1]Won Y M, Yeo T J, Seol D J,et al. A New Criterion for Internal Crack Formation in Continuously Cast Steels[J]. Metallurgical and Materials Transaction B, 2000, 31(4): 779-794.

[2]Pierer R, Bernhard C, Chimani C. A Contribution to Hot Tearing in the Continuous Casting Process[J]. La Revue de Métallurgie-CIT, 2007, 104(2): 72-83.

[3]Rappaz M. A New Hot-tearing Criterion[J]. Metallurgical and Materials Transaction A, 1999, 30(2): 449-455.

[4]Rogberg B. An Investigation on the Hot Ductility of Steels by Performing Tensile Tests on In-Situ Solidified Samples[J]. Scandinavian Journal of Metallurgy, 1983, 12(2): 51-66.

[5]Olsson E A. Methods of Bending Casting in a Continuous Casting Process: Germany, 1124450[P]. 1961-11-14.

[6]Bungeroth A,Schrewe H. Method of Deflecting Towards the Horizontal a Curved Continuously Cast Descending Billet: Germany, 1250973[P]. 1963-05-03.

[7]Schneckenburger E. Continuous Casting Plant for Metals: Germany, 1433022[P]. 1961-05-04.

[8]Bondanelli C. Continuous Casting Process and Plant: Italy, 650613[P]. 1961-04-30.

[9]Voest A G. Continuous Casting Secondary Cooling Zone-in Which Bending and Straightening Rolls Are Positioned According to Given Formula: Germany, 2341563[P]. 1973-08-16.

[10]Vaterlaus A. Continuous Straightening Process[C]//Steelmaking Conference Proceedings. Warrendale:Iron & Steel Soc. of AIME, 1985: 471-487.

[11]Koric S, Thomas B G. Thermo-mechanical Models of Steel Solidification Based on Two Elastic Visco-plastic Constitutive Laws[J]. Journal of Materials Processing Technology, 2008, 197(1/3): 408-418.

[12]Huespe A E, Gardona A, Nigro N. Visco-plastic Constitutive Models of Steel at High Temperature[J]. Journal of Materials Processing Technology, 2000, 102(1/3): 143-152.

[13]Wang Wentao, Guo Xunzhong, Huan Bo,et al. The Flow Behaviors of CLAM Steel at High Temperature[J]. Materials Science & Engineering A, 2014, 599: 134-140.

[14]Rowan M, Thomas B G, Bernhard C,et al. Measuring Mechanical Behavior of Steel during Solidification: Modeling the SSCT Test[J]. Metallurgical and Materials Transaction B, 2011, 42(4): 837-851.

[15]Martin C L, Favier D, Suéry M. Viscoplastic Behaviour of Porous Metallic Materials Saturated with Liquid Part I: Constitutive Equations[J]. International Journal of Plasticity, 1997, 13(3): 215-235.

[16]Kozlowski P F. Simple Constitutive Equations for Steel at High Temperature[J]. Metallurgical Transaction A, 1982, 23(3): 903-918.

[17]El-Bealy M. On the Mechanism of Halfway Cracks and Macro-segregation in Continuously Cast Steel Slabs(Ⅰ). Halfway Cracks[J]. Scandinavian Journal of Metallurgy, 1995, 24(2): 63-80.

[18]Shigeyuki M, Kaname W, Yukio I. Analysis of Bulging in Continuously Cast Slabs[J]. Tetsu to Hagane, 1983, 69(12): 226.

[19]Hibbeler L C, Koric S, Xu K,et al. Thermo-mechanical Modeling of Beam Blank Casting[J]. Iron and Steel Technology, 2009, 22(4): 8-14.

[20]Víctor D, Fachinotti, Alberto C. Constitutive Models of Steel under Continuous Casting Conditions[J]. Journal of Materials Processing Technology, 2003, 135: 30-43.

[21]Wray P J. Effect of Carbon Content on the Plastic Flow of Plain Carbon Steels at Elevated Temperatures[J]. Metallurgical Transaction A, 1982, 13(1): 125-134.

(编辑王旻玥)