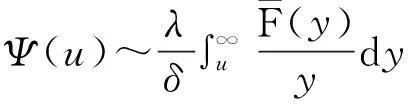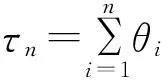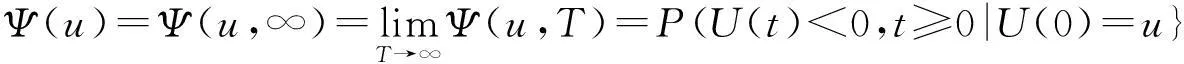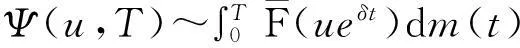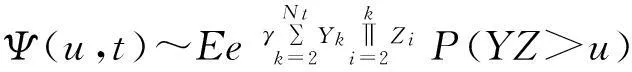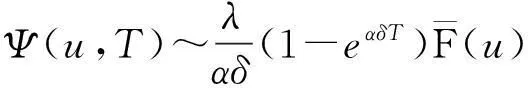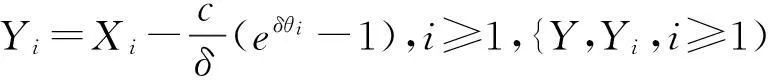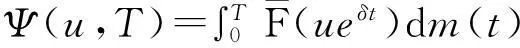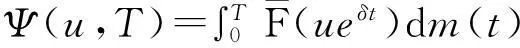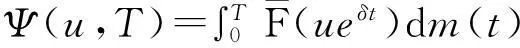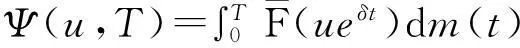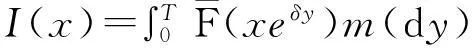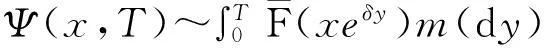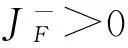重尾分布下常利率风险模型破产概率的研究进展
2015-12-29乔克林,张宁,高渊
重尾分布下常利率风险模型破产概率的研究进展
乔克林,张宁,高渊
(延安大学数学与计算机科学学院,陕西延安716000)
摘要:在重尾分布的条件下,对带常利息力风险模型的破产概率的最新研究进展进行综述。首先,简要介绍经典风险模型及其主要研究成果;其次,重点介绍重尾分布下所建立的带常利息力风险模型的研究成果;最后,对重尾分布在保险实业中的应用前景进行进一步的展望。
关键词:破产概率;常利息力;重尾分布;更新风险模型
中图分类号:O211.9
文献标识码:A
文章编号:1004-602X(2015)01-0009-05
收稿日期:2014-12-26
基金项目:陕西省教育厅自然科学基金(2013JK0576)
作者简介:乔克林(1964—),男,陕西佳县人,延安大学副教授。
Abstract:This article aims at summarizing the development of research on ruin Probabilities in the risk model with constant force of interest in the heavy-tailed distribution.At first,we introduce the classical risk model and its main research results;Then,we mainly introduce research achievements established under constant force of interest in the risk model of heavy-tailed distribution;At last,further the application prospect of heavy-tailed distributions in insurance industry in China is addressed.
风险理论是对保险业所面临的各种风险进行数理分析的理论。而破产理论是风险理论研究的核心问题,它主要针对保险公司如何估计所面临的风险,讨论在一段时间内保险公司发生破产的概率。
瑞典精算师Filip-Lundberg在1903年发表的博士论文开启了破产理论研究的篇章,但是他的工作并不是那么严谨,后来以HaraldCramér为首的Stockholm学派在不断探究中将其严格化,也正是Cramér把Lundberg的工作建立在了非常坚实的数学基础上,才有了现在颇受学者青睐的Filip-Lundberg经典破产模型。
由于破产理论在金融经济领域的应用非常广泛,具有巨大的研究价值,因而许许多多的学者在长期的研究过程中不断地对经典风险模型进行改进,力求其更加符合实际需要。而重尾分布下风险模型的研究是风险理论的前沿问题之一,它对于解决那些灾难性的保险问题很有帮助。因此,近年来许多学者采用不同的方法,从不同的角度对其进行了研究,也得到了许多有用的研究成果。本文旨在对近年来的工作做一个全面系统地梳理,希望能形成一个比较清楚的研究网络,为后续学者的研究指引方向。
1关于Lundberg-Cramér经典破产模型及其主要研究成果
Lundberg-Cramér经典破产模型是现代破产论研究的基本模型和起点。它的基本内容是:设保险公司在时刻t的盈余由下式给出
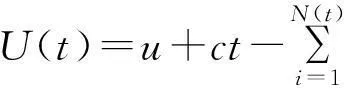
其中:
(1)u(u>0)为保险公司初始准备金;
(2)c(c>0)为保险公司单位时间内收取的保费,即保费率;
(3)Xi表示保险公司第k次的索赔额,且{Xi,i≥1}是恒正的、相互独立与X同分布的随机变量序列,分布为F(x)=P(X≤x),∀x≥0,(F(0)=0);
(4)N(t)则表示截止时刻t所发生的理赔总次数,{N(t),t≥0}是以λ(λ>0)为参数的Poisson过程,且{N(t),t≥0)和{Xi,i≥1)相互独立;
(5)c=(1+θ)λμ,其中θ>0,称为相对安全负载;
(6)调节系数存在唯一性。
在以上假设的基础上,研究经典风险模型得出的主要结果有:


(3)Lundberg-Cramér近似:存在正常数C,使得
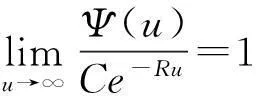
(4)Lundberg不等式:Ψ(u)≤e-Ru,∀u≥0。
2重尾分布下带利息力风险模型的研究进展
2.1 常见重尾分布族及相关定义
定义1对于一个非负随机变量X,对任意的t>0成立,如果矩母函数MX(t)=EetX=∞,就称X是重尾的。否则,如果MX(t)<∞,就称X是轻尾的。
下面介绍一些常见的重尾子族:
L族(长尾分布族):对任意固定的y,分布函数F满足

S族(次指数族):对任意的n≥2,分布函数F满足
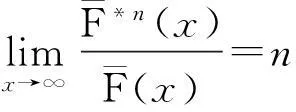
D族(可控变化分布族):对任意的0 S*族:具有有限期望μ>0的分布F满足 ERV族:对某1<α≤β<∞,对任意的y>1,若满足 M族:分布函数F满足 C族:分布函数F满足 S(γ)族:分布函数F在[0,∞]满足 特别的,当γ=0时,S(γ)即亚指数分布族S。 定义2令F为支撑在[0,∞)上的分布函数,对于任意的y>1,记 定义3称两r.v.sX1,X2为负象限相依的(NQD),若对所有的实数x1和x2, P(X1 或等价的, P(X1 见Lehmann(1966)[1]。称r.v.s{Xn,n≥1)}为两两NQD的,若对所有的正整数i≠j,Xi和Xj是NQD的。 自从经典的Lundberg-Cramér破产模型建立以来,不少学者对其模型进行了改进,从模型、研究对象、研究方法等方面做了全方位的推广,其中一种推广就是考虑利息因素,从而引入了带常利息力的经典模型。即t时的盈余可以表示为: 其中,δ为常数利息力。该模型对现实有很强的描述能力,因此成为当前保险理论界和实务界特别关注的对象。目前不少学者对此都颇有研究,比较前沿的首先应该提到Klüppelberg & Stadtmuller[2],他们得到了:在常数利息力δ的假定下以及在经典模型的场合,有如下的结果: 这里,假设索赔额属于R-α。 其后,在索赔额属于强次指数分布的假定下,Asmussen[3]和Asmussen等[4]分别证明了 (1) Kalashnikov and Konstantinides[5],Konstantinides[6]和Tang[7,8]等把研究扩展到更大的重尾分布族,其中Tang[7]得到了在泊松场合以及次指数索赔额的假定下,得到了(1)式。Tang[8]得到了索赔额服从次指数分布的带常利率的复合Poisson模型的有限时破产概率。 特别地,文献[2]以及[7]中的方法还在本质上依赖于索赔额的正则性。 下文将带常利息力的经典模型中齐次Poisson过程推广到一般的更新过程,就得到如下模型: (a)索赔额{Xi,i≥1}构成一个独立同分布非负随机变量序列,具有共同的分布F和有限的期望μ; (b)两次索赔到来的时间间隔{θi,i≥1)是独立同分布的非负随机变量,具有共同的分布G和有限的期望m>0,且与序列{Xi,i≥1)相互独立; (d)保险公司的费率(单位时间收到的保费)c为常数。 设初始资本为u,令δ>0是常利率,也就是说,时间t以后一个资本x就变为xeδt。我们用U(t)来定义到时间t时的总资本,则 (2) 此处当U(t)>0时表示保险公司的内部总资本有剩余。由此我们可以在有限时间T内的破产概率Ψ(u,T)满足下面式子 ψ(u,T)=P{U(t)<0,0≤t≤T|U(0)=u}。 而无限时破产概率定义为 对带利息力的更新风险模型的研究在近些年比较热门,其主要研究成果如下: 定理2[10]在模型(2)中,索赔额{Xi,i≥1)是独立同分布的随机变量,分布函数F∈S,则有限时间T的破产概率可表示为 定理3[11]在带有固定利息δ>0的更新模型中,如果F∈S(γ)∩R-∞,则对任意的有0 以下是带利息力的更新风险模型的特殊情况的结论: 定理4[12]在索赔额服从Pareto分布,索赔来到过程为泊松风险过程,则在时间区间[0,T]内的有限时间的破产概率满足如下的渐近公式: 定理5[11]在带有固定利息δ>0的复合Poisson模型中,如果F∈S(γ),则对任意的0 在市场需求多元化的条件下,保险公司经营的险种越来复杂多元化、市场化、国际化,而各索赔之间、各险种之间、索赔额和险种之间往往都是具有相关性的。故引入经典的相依情况—负相依的理论,研究索赔额在负相依情况下的破产概率渐近表达式。 若索赔额Xi是负相依同分布的随机变量,则上述模型(2)称为负相依常利率更新风险模型。 近年来,chen和Kai W.Ng(2007)[13]利用纯概率的方法研究了索赔额{Xn,n≥1}为两两NQD,有共同分布F∈εRV(-α,-β)且索赔间隔时间为i.i.d的破产概率的渐近公式。其结果如下: 定理6在上述模型(2),若索赔额{Xn,n≥1}为两两NQD的,有共同分布F∈εRV(-α,-β),索赔时间间隔独立同分布,则有限时破产概率为: 在随机变量服从两两负相依关系和模型不变的条件下,王跃宝等[14]考虑在F∈C族情形下,破产概率的渐近公式。其结果如下: 定理7在上述模型(2),若索赔额{Xn,n≥1}为两两NQD的,有共同分布F∈C,则有限时间T的破产概率满足 在此基础上,江涛[15]进一步将模型推广到F∈D∩L的情况时,破产概率的渐近公式。其结果如下: 定理8在上述模型(2),若索赔额{Xn,n≥1}为两两NQD的,有共同分布F∈D∩L,则有限时间T的破产概率满足 随后,吴永等[16]又将模型推广到F∈S的情况下,等到如下结果: 定理9在上述模型(1),若索赔额{Xn,n≥1}为两两NQD的,有共同分布F∈S,则有限时间T的破产概率满足 为了使模型的描述更符合保险公司的实际,李景芝[17]在索赔额{Xn,n≥1}为两两NQD,有共同分布F∈D的基础下,进一步假定索赔发生的时间间隔θn,n≥1也具有某种负相依的结构,并得出了在有限时间和无限时间的破产概率,其结果如下: I(x)≤Ψ(x,T)≤L-1FI(x)。 特别地,若F∈C,则 3展望 在金融保险域中,重尾分布破产概率作为破产论的一个重要分支,近来,引起众多学者对它的研究兴趣,也在这方面取得了丰富的研究成果。本文主要综述了带常利息力的风险模型的破产概率的研究进展。但文中仍有许多值得我们进一步研究探讨的问题:第一,对带常利息力的各风险模型的研究仍停留在理论研究阶段,故在后续的工作中,我们将会深入研究并完善已有的结论,并通过实证分析,让其不仅具有重大的理论意义,而且也具有更加重要的实际经济意义。第二,文中各风险模型下破产概率的研究成果都是在一定假设条件下成立的,如对索赔额、索赔发生的时间间隔的假定,故对于弱化模型的条件从而得到更符合保险实际的结果,也有待于进一步的研究探讨。 参考文献: [1]Lehmann,E.L.Some concepts of dependenc[J].Annals of Mathemtical Statistics,1966,37(5),1137-1153. [2]Klüppelberg C,Stadtmuller U.Ruin probabilities in the presence of heavy-tails and interest rates[J].Scand Actuar J,1998,1:49-58. [3]Asmussen S.Subexponential asymptotics for stochastic processes: extremal behavior,stationary distributions and first passage probabilities [J]. Ann Appl Probab,1998,8(2):354-374. [4]Asmussen S,Kalashnikov V,Konstantinides D,et a1.A local limit theorem for random walk maxima with heavy tails[J].Statist Probab Lett,2002,56(4):399-404. [5]Kalashnikov,V.,Konstantinides,D. Ruin under interest force and subexponential claims:a simple treatment[J].Insurance Math.Econom,2000,27(1):145-149. [6]Konstantinides,D.,Tang,Q.,Tsitsiashvili,G. Estimates for the ruin probabilityin the classical risk model with constant interest force in the presence of heavy tails[J]. Insurance Math.Econom,2002,31(3):447-460. [7]Tang Qihe. Asymptotic ruin probabilities of the renewal model with constant interest force and regular variation[J].Scand Actuar J,2005 (1): 1-5. [8]Tang Qihe. The finite-time ruin probability of the compound Poisson model with constant interest force.[J].Appl Probab,2005,43(3):608-619. [9]汪春华.一类带常利率的更新过程的研究[J].宁波职业技术学院学报,2007,11(5):6-9. [10]吴永,邵明阳.重尾索赔下常利力更新风险模型的破产概率[J].重庆理工大学学报,2010,24(10):97-100. [11]王晶晶.常值利息力下破产概率的渐进估计[J].安庆师范学院学报(自然科学版),2012,18(1):30-46. [12]江涛.正则变化场合常利息力度的破产概率[J].数学的实践与认识,2008,38(8):46-50. [13]Chen Y,Kai W N.The ruin prbability of the renewal model with constant interest force and negatively dependent heavy-tailed claims[J].Insurance Math.Econom,2007,40(3):415-423. [14]YuebaoWang,KaiyongWang,JingzhiLi. Finite-time Ruin Probability w- ith NQD Dominated Varying-tailed Claims and NLOD Inter-arrival Times[ J]. Jrl Syst Sci & Complexity,2009,22:407-414. [15]Tao Jiang.Ruin Probability with Constant Interest Force and Negatively Dependent Insurance Risk[ C]/ / Proceedings of the World Cong- ress on Engineering. London:[s.n.],2009. [16]Shao M,Wu Y.Ruin Probability with Negatively Dependent and Subexponential claims[J].The International Workshop on Economics,2011. [17]LiJ.,Wang,K.,Wang,Y.Finite-time ruin probability with NQD dominated vaxying-tailed claims and NLOD inter-arrival times[J].accepted by Journal of Systerns science and Omplexity,2007. [18]Wang yuebao,Yangyang.The structure and precise moderate deviations of random variables with dominatedly varying tails[J].Journal of Systems Science and Complexity 2005,18(2). [责任编辑毕伟] Research Progress on Ruin Probabilities in the Risk Model with Constant Interest Force QIAO Ke-Lin,ZHANG NING,GAO YUAN (College of Mathematics and Compnter Science,Yan'an University,Yan'an 716000,China) Key words:ruin probabilities; constant force of interest; heavy- tailed distribution; renewal risk model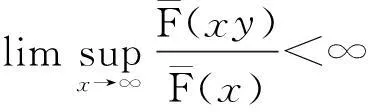
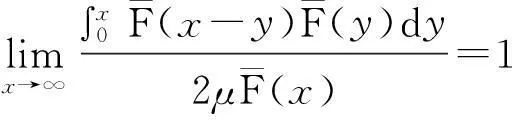

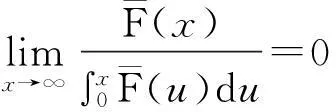
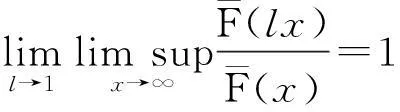
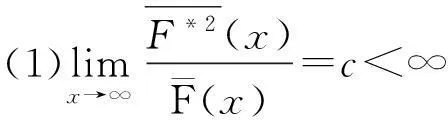
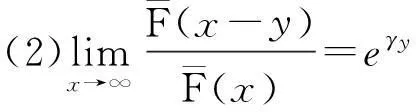

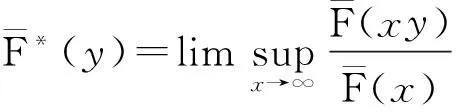
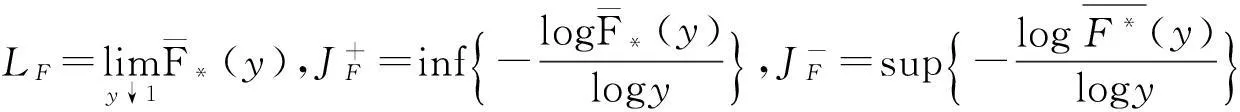

2.2 带利息力风险模型破产概率的研究进展