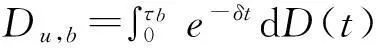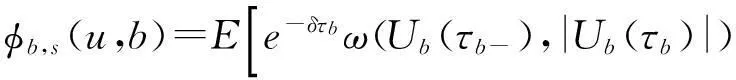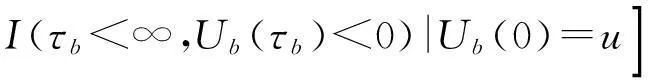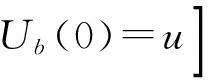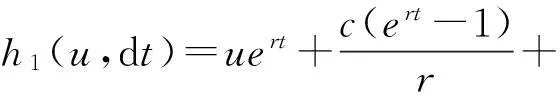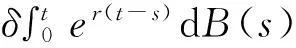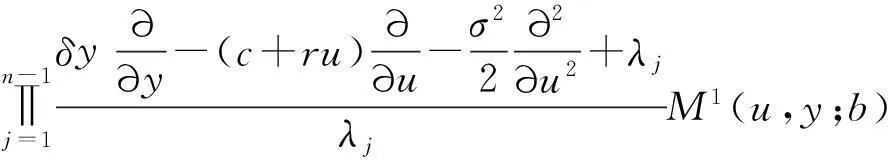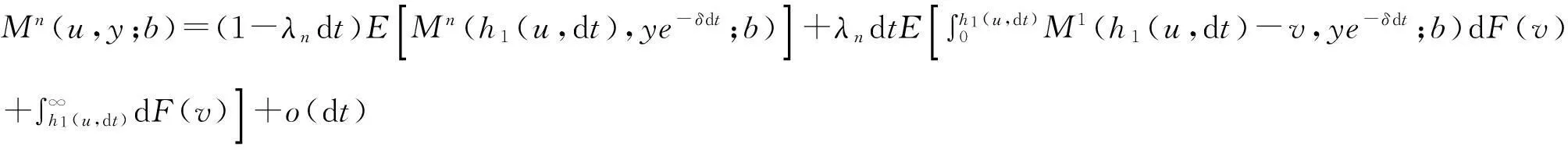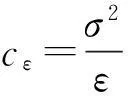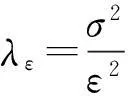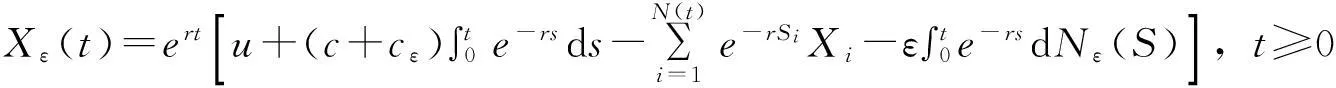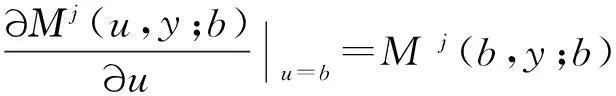常利率环境下带扰动的广义Erlang( n)风险过程的Gerber-Shiu函数问题

常利率环境下带扰动的广义Erlang(n)风险过程的Gerber-Shiu函数问题

王健，王传玉，胡莎娜

(安徽工程大学数理学院，安徽芜湖241000)

摘要：在常利率环境条件下研究在带扰动的广义Erlang(n)风险过程中保险公司的Gerber-Shiu函数问题。在障碍策略下，得出其矩母函数所满足的积分-微分方程及方程的边界条件和Gerber-Shiu函数所满足的积分-微分方程及方程的边界条件。

关键词：常利率；广义Erlang(n)风险模型；Gerber-Shiu函数

中图分类号：O211.9

文献标识码：A

文章编号：1004-602X(2015)01-0003-04

收稿日期：2014-11-21

基金项目：国家自然科学基金项目(61203139)；安徽省重点教研项目(2012jyxm277)

作者简介：王健(1989—)，男，安徽六安人，安徽工程大学在读硕士研究生。

Abstract：We consider the Gerber-Shiu function in a generalized Erlang(n) risk process perturbed by diffusion with a constant interest under a dividend barrier strategy. Under such a strategy,Integro-differential equations with certain boundary conditions for the moment generating functions and the Gerber-Shiu function are derived.

破产理论的研究可以追溯到瑞典精算师Filip Lundberg在1903年发表的博士论文[1]。在这篇论文中，Lundberg首次提出了一类重要的随机过程Poisson过程。保险公司支付红利给股东。De Finetti在1957年一文[2]中首先在贝努力模型中提出了红利障碍策略，以此来更真实地反映保险投资组合的盈余现金流。然后，学者们在不同的模型中研究了不同的分红策略和Gerber-Shiu函数。如Albrecher et al.(2005a，2005b)[3,4]，Avanzi et al.(2007)[5]，Gao和Yin(2008a)[6]等。

Shuangming Li(2005)[7]一文中在障碍分红策略下带扰动的广义Erlang(n)风险模型中研究了保险公司盈余过程的瑕疵更新方程。Gao和Yin(2008)[6]一文中在障碍分红策略下常利率环境中研究了带几何布朗运动的广义Erlang(n)风险模型，推导出满足模型的Gerber-Shiu函数的积分-微分方程及边界条件，同时给出特殊情形的详细解。

本文将在以上的障碍策略下，在常利率环境中研究带扰动的广义Erlang(n)风险模型的Gerber-Shiu函数问题。

1模型的建立

本文考虑盈余过程：

引入利率r≥0，则在时刻t时的盈余过程为

(1)

其中Si为第i次索赔发生的时刻。

模型(1)，我们引进一个障碍策略，则改进的盈余过程{Ub(t),t≥0}表示为

dUb(t)=cdt+rUb(t)dt-dS(t)+σdB(t),

0≤Ub(t)

(2)

然后，我们感兴趣的矩母函数表示为

M(u,y;b)=E[eyDu,b|Ub(0)=u]。

类似于Gerber和Landry(1998)[7]一文中，我们将贴现惩罚函数分为两部分

φb(u,b)=φb,s(u,b)+φb,d(u,b)，

这一贴现惩罚函数是由索赔所引起的。

这一惩罚函数是由扰动所引起的，且令

ω(0,0)=1。

2积分-微分方程

定理2.1当0≤u

(3)

边界条件为：

(4)

当j=1，…,n时有

(5)

证明：运用马尔可夫性质中指数分布的无记忆性，通过分解索赔次数为n个独立的指数分布的和的风险过程，其指数分布的系数分别为λ1,λ2,…,λn，得：

当风险过程达到第i步时，令Mj(u,y;b)表示Du,b的矩母函数，且

M(u,y;b)=M1(u,y;b)。

当0≤u

(6)

泰勒展开得：

Mj(h1(u,dt),ye-δdt;b)=Mj(u,y;b)+

(7)

将(7)代入(6)中，两边同除以t，得：

λjMj+1(u,y;b)=0，

整理得：

(8)

由(8)得：

Mn(u,y;b)=

类似地，当j=n时有：

推导出：

(9)

通过(8)、(9)得到方程(3)。

如果u=0，则立刻发生破产，没有红利支付，这时Mj(0,y;b)=1，j=1，…，n，由(8)式得(4)式。

当ε→0时有：

由保险公司盈余过程的弱收敛性，当{N(t),

当ε→0时，由(8)式得(3)式。定理得证。

定理2.2当0≤u

(10)

边界条件为：

=0，j=1,…,n

(11)

和

=0，j=1,…,n

(12)

证明：设φb,s(j)(u,b)表示当风险过程达到第j(j=1,…，n)步时的惩罚函数。

令φb,s(1)(u,b)=φb,s(u,b)。这样当0≤u

j=1，…，n-1可得

由于e-δdt=1-δdt+o(dt)，我们得到

(13)

泰勒展开有

(14)

(13)式两边同时对dt求导，并令dt→0，运用方程(14)，可得

整理为

(15)

类似地，当j=n时，我们得

推导出

(16)

由(15)式有

(17)

由(16)(17)式得(10)式。

类似定理2.1的证明，可得(13)式。

定理2.3当0≤u

边界条件为：

和

=0，j=1，…，n。

定理2.4当0≤u

边界条件为：

和

=0，j=1，…，n。

证明：由定理2.2和定理2.3，且φb(u,b)=

φb,s(u,b)+φb,d(u,b)可得证。

参考文献：

[1]Lundberg F I.Approximerad Framstallning av Sannolikhersfunktionen.Aterforsakring av Kollektivrisker [D].Almqvist Wiksell,Uppsala,1903.

[2]De Finetti,B.Su unimpostazione alternativa dell teoria collettiva del rischio[J].Transactions of the XVth International Congress of Actuaries,1957,32(2):433-443.

[3]Albrecher H,Claramunt M M,Marmol M.On the distribution of dividend payments in a Sparre Andersen model with generalized Erlang(n) interclaim times[J].Insurance: Mathematics and Economics,2005a,37: 324-334.

[4]Albrecher H,Hartinger J,Tichy R.On the distribution of the dividend payment and the discounted penalty function in a risk model with a linear dividend barrier[J].Scandinavian Actuarial Journal,2005b,2: 103-126.

[5]Avanzi B,Gerber H U,Shiu E S W.Optimal dividends in the dual model[J].Insurance: Mathematics and Economics,2007,41: 111-123.

[6]Gao H L,Yin C C.A perturbed risk process compounded by a geometric Brownian motion with a dividend barrier strategy[J].Applied Mathematics and Computation,2008a,205:45-64.

[7]Gerber,H.U.,Landry,B.On the discounted penalty at ruin in a jump diffusion and the perpetual put option[J].Insurance: Mathematics and Economics,1998,22: 263-276.

[8]Wan,N.Divident payments with a threshold strategy in the compound Poisson risk model perturbell by diffusion[J].Insurance:Mathematics and Economics,2007,40:509-523.

[责任编辑毕伟]

The Gerber-Shiu Function Problems of Ruin in a Generalized

Erlang(n) Risk Process Perturbed by Diffusion

with Constant Interest

WANG JIAN,WANG Chuan-yu,HU Sha-na

(School of Mathematics and Physics,Anhui Polytechnic University,Wuhu 241000,China)

Key words：a constant interest; the generalized Erlang(n) risk process by diffusion; the Gerber-Shiu function