关于Diophantine方程 x 3-1=3pqy 2

关于Diophantine方程x3-1=3pqy2

冯蕾，赵西卿，刘建

(延安大学数学与计算机科学学院，陕西延安716000)

摘要：主要利用递归数列、同余式、平方剩余以及Pell方程解的性质，证明了：设素数p≡q≡1(mod12)，(p/q)=-1，Diophantine方程x`3-1=3pqy`2仅有整数解，即(x,y)=(1,0)。

关键词：Diophantine方程；同余式；平方剩余；Pell方程

中图分类号：O156.4

文献标识码：A

文章编号：1004-602X(2015)01-0001-02

收稿日期：2014-11-04

基金项目：陕西省教育厅科研计划资助项目(2013JK0557)；延安大学自然科学专项基金项目(YDZ2013-05)；延安大学研究生教育创新计划项目

作者简介：冯蕾(1989—)，女，陕西子长人，延安大学在读硕士研究生。

Abstract：Using recurrent sequence , congruence , quadratic residue and Pell equation to prove that:the Diophantine equation x`3-1=3pqy`2 only has interger solution(x,y)=(1,0) when p,q are primes with p≡q≡1(mod12) and (p/q)=-1.

1主要结论及证明

关于Diophantine方程x3-1=Dy2(D>0，D无平方因子，x,y∈Z)，罗明[1]，高丽[2]，李鑫[3]等就D为不同因数做过一些研究.本文证明了下面的定理：

定理设素数p≡q≡1(mod12)，(p/q)=-1，则丢番图方程

x3-1=3pqy2

(1)

的整数解仅有(x,y)=(1,0)。

证明由题知式(1)可表为(x-1)(x2+x+1)=3pqy2，(x-1,x2+x+1)=1或3。

情形一，当(x-1,x2+x+1)=1时，设y=uv，(u,v)=1，方程(1)可分以下八种情况进行研究

(Ⅰ)x-1=3pqu2,x2+x+1=v2；

(Ⅱ)x-1=u2,x2+x+1=3pqv2；

(Ⅲ)x-1=3u2,x2+x+1=pqv2；

(Ⅳ)x-1=pqu2,x2+x+1=3v2；

(Ⅴ)x-1=3pu2,x2+x+1=qv2；

(Ⅵ)x-1=qu2,x2+x+1=3pv2；

(Ⅶ)x-1=3qu2,x2+x+1=pv2；

(Ⅷ)x-1=pu2,x2+x+1=3qv2。

以下讨论这八种情况：

(Ⅰ)由第二式得x=0,1，代入第一式发现均不满足条件，故方程(1)无整解。

(Ⅱ)因u2≡0,1(mod3)，由同余性质知，若u2≡0(mod3)，与(u2,3pqv2)=1矛盾；若u2≡1(mod3)，则x-1=u2≡1(mod3)，x≡2(mod3)，从而3pqv2=x2+x+1≡7≡1(mod3)，显然不成立，故方程(1)无整解。

(Ⅲ)由第一式得，x-1=3u2≡0(mod3)，即有x≡1(mod3)，则有pqv2=x2+x+1≡3≡0(mod3)，与(3u2,pqv2)=1矛盾，故方程(1)无整解。

(Ⅳ)由题知，第二式可化为(2x+1)2-3(2v)2=-3，将第一式代入上式得(2pqu2+3)2-3(2v)2=-3，故方程X2-3Y2=-3的全部解由以下两个非结合类给出[4]

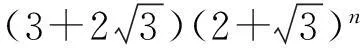
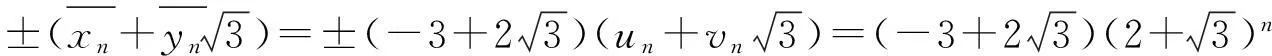
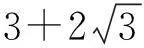
un+2=4un+1-un,u0=1,u1=2；

(2)

vn+2=4vn+1-vn,v0=0,v1=1；

(3)

xn+2=4xn+1-xn,x0=3,x1=12；

(4)

xn+2=6vn+3un。

(5)

若n≡1(mod2)时，把(2)，(3)代入(5)得到

xn=6(4vn-1-vn-2)+3(4un-1-un-2)=24vn-1+12un-1-6vn-2-3un-2=…

=24(vn-1-vn-3+…+v2)+12(un-1-un-3+…+u2)+(6v1+3u1)

=24(vn-1-vn-3+…v2)+12(un-1-un-3+…+u2)+12。

当xn≡0(mod2)，3=±xn-2pqu2≡0(mod2)，显然不成立；当xn≡0(mod3)时，±xn-3=2pqu2≡0(mod3)，则有pqu2≡0(mod3)与(pqu2,3v2)=1矛盾。故方程(1)无整解。当xn≡0(mod4)，xn≡0(mod6)，xn≡0(mod12)时，可类似证明，且方程(1)无整解。

若n≡0(mod2)，同理可证方程(1)无整解。

(Ⅴ)由题知，第二式可化为(2x+1)2-4qv2=-3，将第一式代入第二式得(6pu2+3)2-4qv2=-3，对上式两边同取模p有qv2≡3(modp)，而p≡q≡1(mod12)，(p/q)=-1。所以(qv2/p)=-1，但(3/p)=1，与之矛盾。故方程(1)无整解。

(Ⅵ)证明类似于(V)得方程(1)无整解。

(Ⅶ)证明类似于(Ⅲ)得方程(1)无整解。

(Ⅷ)由题知，第二式可化为(2x+1)2-12qv2=-3，将第一式代入第二式得(2pu2+3)2-12qv2=-3，对上式两边同取模p有qv2≡1(modp)。而p≡q≡1(mod12)，(p/q)=-1，所以(qv2/p)=-1，但(1/p)=1，与之矛盾。故方程(1)无整解。

通过对以上八种情况进行讨论研究知方程(1)无整解。

情形二，当(x-1,x2+x+1)=3，且x≠1时，有3|(x-1)，不妨设x-1=3x1，则x=3x1+1将其代入方程(1)得(3x1+1)3-1=3pqy2，对上式两边同取模3有2≡0(mod3)，显然不成立。所以方程(1)无整数解。当x=1，y=0时即满足方程(1)，故方程(1)只有平凡整数解(x,y)=(1,0)。

综上所述，方程(1)仅有整数解(x,y)=(1,0)，即定理得证。

参考文献：

[1]罗明.关于不定方程x3±1=14y2[J].重庆交通学院学报(自然科学版)，1995，41(3)：112-115.

[2]高丽，鲁伟阳.关于丢番图方程x3+1=301y2[J].广西科学，2014，21(3)：290-292.

[3]李鑫，梁艳华.关于不定方程x3-1=111y2[J].西南师范大学学报(自然科学版)，2009，34(1)：12-15.

[4]柯召，孙琦.谈谈不定方程[M].上海：上海教育出版社，1980.

[责任编辑毕伟]

On the Diophantine Equationx3-1=3pqy2

FENG LEI,ZHAO Xi-qing,LIU JIAN

(College of Mathematics and Computer Science,Yan'an University,Yan'an 716000,China)

Key words：Diophantine equation; recurrent sequence; congruence sequece; Pell equation