基于矩阵博弈的两机攻防对抗空战仿真
2015-12-28车竞钱炜祺和争春
车竞,钱炜祺,和争春
(中国空气动力研究与发展中心 计算空气动力学研究所,四川 绵阳621000)
0 引言
空战决策是指在空战过程中作战双方如何根据作战态势以及作战环境选择战胜对方和保存自己的攻防策略选择方法,其中比较有影响力的方法包括:微分对策法、专家系统法、矩阵博弈法、智能微分对策法及神经网络法等[1]。
矩阵博弈法是空战对策研究中提出较早、技术最成熟的方法之一,实质是微分对策的离散化。其基本思路是:首先列举空战对抗中双方可采取的典型机动飞行方式,然后把各种机动方式组合成不同的对抗模式,得到对抗模式矩阵(支付矩阵),最后根据希望达到的战术目的,对矩阵中每一种对抗模式计算相应的支付函数值进行量化打分。根据计算出的各模式组合的得分总数,选出得分最高者作为飞行轨迹[2]。
空战对抗中的传统矩阵博弈方法是寻找鞍点的过程,即红蓝双方分别利用最小-最大策略选择支付矩阵中的支付函数值,得到各自的飞行模式。当支付矩阵可分时,鞍点存在,此时双方的支付函数值相同,且均能获得最保守的最大利益[3]。但由于该方法不考虑空战双方的机动策略,而且鞍点也往往不存在,因此应用上有一定局限性。本文对传统的矩阵博弈进行了扩展,将飞机的机动分为攻击和逃避两大策略,根据策略不同选择不同的支付函数计算公式;其次是摒弃了鞍点概念,红蓝双方各自建立自己的支付矩阵,并各自根据最小-最大策略选择支付矩阵中的支付函数值,得到各自的飞行模式;最后通过示例进行了仿真验证。
1 矩阵博弈问题描述
矩阵博弈建立在支付矩阵的基础上,而支付矩阵则是在双方完成某一特定机动动作后由支付函数计算得到,因此必须为双方建立合适的机动动作库。
1.1 支付矩阵
文献[3]提出较为常用的7种空战机动方式:(1)定常平飞;(2)最大加速平飞;(3)最大减速平飞;(4)最大负载爬升;(5)最大负载下降;(6)最大载荷右转;(7)最大载荷左转。文献[4-6]分别提出16,25,22种机动动作,例如:(1)直线飞行;(2)定常盘旋;(3)前置跟踪;(4)俯冲增速;(5)斜拉起;(6)急拉起;(7)纯跟踪;(8)半斤斗;(9)跃升半滚;(10)高过载上滚;(11)高过载下滚;(12)规避转弯;(13)急规避;(14)增速转弯;(15)蛇形机动;(16)筒滚;(17)急盘降;(18)大坡度外转;(19)回转;(20)急上升转弯;(21)下降急转;(22)下滑倒转;(23)半滚倒转;(24)高速 Yo-Yo;(25)低速 Yo-Yo等。
本文以7种空战机动方式为例,空战双方会形成49种对抗模式,从而可建立双方各自立场上的支付矩阵。红方的支付矩阵如表1所示。

表1 红方支付矩阵Table 1 Score matrix of red plane
表中,fij(t)表示蓝方和红方分别采用i和j机动策略对抗结局的评分,分值越大,代表红方优势越大。传统矩阵博弈中,红方总是选择分数最大的机动方式,而蓝方正相反,选择的结果是达到了博弈论中的平衡点,即“鞍点”。本文则针对红方和蓝方分别建立各自的支付矩阵,并根据最小-最大原则各自选择分数最大的机动方式。
1.2 支付函数
支付矩阵中,分数值由支付函数计算。支付函数实际上是对完成相应机动动作后双方态势、攻击优势的估计,通常是相对方位、相对距离、速度和地形等自变量的函数。例如,文献[7]中给出的一种形式为:

式中:s为总得分数;s1为与相对方位角有关的分数;s2为与相对距离有关的分数;s3为加速度的得分数。
(1)方位贡献
图1为红蓝双方相对位置关系。站在红方立场,由图1可知,当红方(R)进攻时,其方位角贡献为:

当红方逃避时,其方位角贡献为:

蓝方(B)的方位角贡献计算方法与红方相同。(2)距离贡献
当红方攻击时,希望双方距离越来越近。此时,距离贡献为:

当红方逃避时,希望双方的距离越来越远。此时,距离贡献为:

式中:r为双方距离;rm为攻击方导弹射程。蓝方的距离贡献计算方法与红方相同。
(3)总的贡献
当优先改变距离因素时,s=s2;当优先改变方向因素时,s=s1;当同时考虑距离改变和方向改变时,s=s1s2。

图1 红蓝双方相对位置关系Fig.1 Relative position of red and blue planes
2 机动动作库设计
考虑7种基本机动动作组成动作库,分别是:
(1)定直对称平飞:在水平面内匀速飞行,倾侧角γv=0°,保持高度稳定,推力由阻力平衡确定。
(2)最大加速平飞:水平面内最大加速飞行,γv=0°,保持高度稳定,推力开到“加力”状态。
(3)最大减速平飞:水平面内最大减速飞行,γv=0°,保持高度稳定,推力开到“怠速”状态。
(4)最大过载爬升:分为三个阶段,首先以最大法向过载拉起,γv=0°,推力开到“加力”状态,直到倾角达到指定倾角;然后保持该倾角加速爬升,直到爬升高度达到指定高度;最后改出成水平定直飞行状态(1)。
(5)最大过载俯冲:分为三个阶段,首先以最大过载下压,飞机翻转γv=180°,推力开到“加力”状态,直到倾角达到指定倾角;然后飞机翻转γv=0°,维持当前倾角俯冲,直至俯冲高度达到设定值;最后改出成水平定直飞行状态(1)。
(6)最大过载右转:分为两个阶段,首先在保持高度的情况下以最大法向过载、最大倾侧角右转,推力开到“加力”状态,直至达到指定速度偏角;然后γv=0°,改出成水平定直对称飞行状态(1)。
(7)最大过载左转:分为两个阶段,首先在保持高度的情况下以最大法向过载、最大倾侧角左转,推力开到“加力”状态,直至达到指定速度偏角;然后γv=0°,改出成水平定直对称飞行状态(1)。
3 仿真示例
以两架F-16战斗机挂载空空导弹为例进行空战仿真验证。设置蓝方在重量、推力以及机动性方面稍弱于红方。假设:当一方进入对方的雷达扫描范围和距离时便被发现;当一方同时也进入对方导弹的发射角范围和射程时,定义为被锁定,此时仿真结束。
3.1 两机对抗仿真示例1
设置红方初始位置坐标为(0,11,0)km,初始速度为 235.8 m/s,初始航迹倾角和偏角为(0°,0°),质量为7 000 kg,发动机加力系数为1.62。蓝方初始位置坐标为(20,13,3)km,初始速度为235.8 m/s,初 始航迹倾角和偏角为(0°,-15°),质量为9 000 kg,发动机加力系数为1.42。
设置双方机动原则为:未被对方发现时采取“攻击”原则,被对方发现时采取“逃避”原则;当双方互相发现时,由于红方参数占优,故红方依然“攻击”,蓝方“逃避”。
红方支付函数采取同时考虑方向和距离改变的方式,蓝方“逃避”时采取“优先改变方向”模式。设置仿真时长为500 s,每个机动动作为20 s,仿真积分步长0.2 s。
双方飞行过程中的机动动作如表2所示,空战航迹如图2和图3所示。

表2 红蓝双方追逃仿真示例1的机动动作与状态Table 2 Tactical actions and stations in the first simulation for red and blue planes
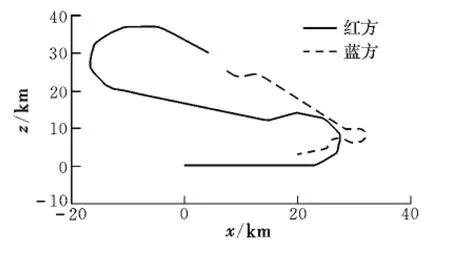
图2 仿真示例1的x-z航迹Fig.2 x-z flight path of the first simulation

图3 仿真示例1的t-y航迹Fig.3 t-y flight path of the first simulation
由仿真过程可以看出:在初始条件下,红方处于有利地位首先发现并攻击蓝方,但蓝方通过快速改变方向迅速摆脱了红方,并且逐渐地取得有利地位,期间双方数次发现并攻击对方。由于蓝方“逃避”时采用“优先改变方向”的策略,因此最终取得制胜位置,锁定了红方。
3.2 两机对抗仿真示例2
将红方“逃避”时的策略设置为“优先改变方向”,其余设置与示例1相同。双方空战航迹如图4和图5所示,飞行过程中的机动动作如表3所示。
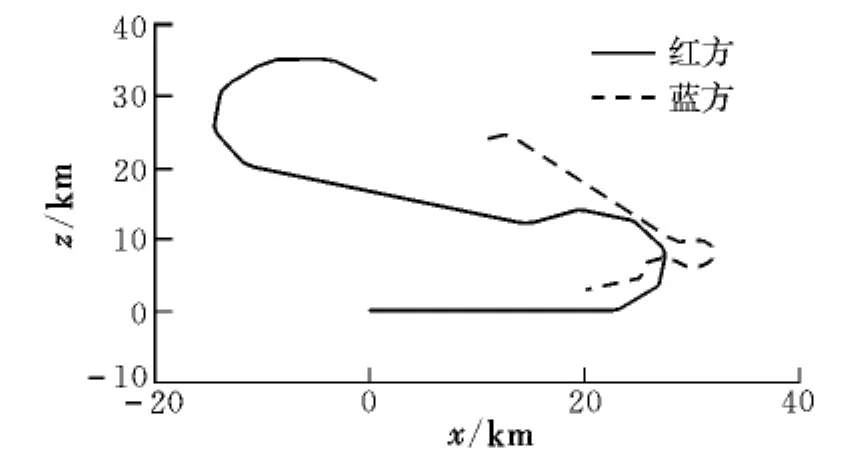
图4 仿真示例2的x-z航迹Fig.4 x-z flight path of the second simulation

图5 仿真示例2的t-y航迹Fig.5 t-y flight path of the second simulation

表3 红蓝双方追逃仿真示例2的机动动作与状态Table 3 Tactical actions and stations in the second simulation for red and blue planes
从仿真过程可以看出:由于红方在“逃避”时采取“优先改变方向”策略,因此在仿真181.8 s被蓝方发现时红方采用第一种机动动作而不是示例1中的第二种机动动作,从而在飞行323.2 s时提前锁定蓝方,获得制胜位置。
4 结束语
本文建立了基于7种机动动作库的矩阵博弈空战仿真模型。在该模型中,改变了传统矩阵博弈双方基于同一支付矩阵求鞍点的模式,分别建立对策双方各自的支付矩阵,根据各自“攻击”还是“逃避”策略选择支付函数的形式,并采用最小-最大原则选择机动动作,完成了两例战机的空战数值仿真验证。仿真结果表明,当战机处于劣势时,大机动改变两机相对方位角关系是尽快获得有利位置的重要手段。
[1] 于梅祥,李一波.无人战斗机空战对策研究综述[J].沈阳航空工业学院学报,2009,26(1):23-25.
[2] 王义宁,姜玉宪.空战对策的发展现状与未来[J].电光与控制,2000,7(2):13-17.
[3] Fred Austin,Giro Carbone,Michael Falco,et al.Automated maneuvering for air-to-air combat[R].AIAA-87-2393,1987.
[4] 朱宝鎏.作战飞机效能评估[M].第2版.北京:航空工业出版社,2006:165.
[5] 胡秉科.歼击机一对一空战模拟系统及其应用[J].航空系统工程,1992(5):17-25.
[6] 梁学政.双机空战的仿真与分析[J].火力与指挥控制,1994,19(4):8-15.
[7] 吴云洁,宋立国,姜玉宪.飞行综合控制系统空战决策方法[J].北京航空航天大学学报,1999,25(3):272-274.
