峰值电流模式控制数字移相全桥变换器的分析与设计
2015-12-28杜建华
王 均 ,杜建华 ,纪 婧 ,马 皓
(1.浙江大学电气工程学院,杭州 310027;2.北京控制工程研究所,北京 100190)
引言
数字控制移相全桥软开关变换器广泛应用于DC/DC电源,针对其数字控制策略,已有大量文献进行了研究[1-3],但都相当局限。 文献[1]只在数字控制单电压环下进行的分析与设计;文献[2]提出可以使用数字控制实现平均电流模式移相全桥软开关,但是对环路的分析建模都使用了传统的数字重设计法;文献[3]给出了电流峰值控制的移相全桥的方案,但没有涉及到软开关的分析设计相关内容。关于峰值电流模式控制,国内外研究主要集中在模拟控制电流内环的小信号建模与分析[4]。而对于峰值电流模式控制数字移相全桥变换器方面的研究少有涉及。然而峰值电流所具有的动态响应快,磁通自动平衡以及数字控制设计灵活,可靠行强等优点,使其在移相全桥变换器上的应用具有很好的发展前景。
本文建立了数字控制峰值电流模式下移相全桥变换器的离散域模型,分析了斜坡补偿、漏感和数字控制延时对数字移相全桥系统稳定性的影响。在此基础上,设计了系统补偿函数,并对比了直接数字设计和数字重设计方法。实验证明了理论建模和分析的准确性。
1 移相全桥变换器小信号模型
移相全桥变换器是一种带隔离变压器的Buck类变换器,但是由于移相全桥存在占空比的丢失,两者的小信号模型并不能等同,其拓扑如图1所示。

图1 移相全桥变换器拓扑Fig.1 Phase-shift full-bridge converter topology
关于移相全桥变换器的小信号模型建模,国外已经有学者做过相关工作。文献[5]给出了2个重要传递函数,即

其中,Rd=4n2Lrfs。
2 数字控制系统分析与设计
对于系统环路建模,考虑到主功率级和峰值电流控制环是在模拟电路下工作,因此能够直接在连续域内进行设计。而电压外环是通过数字处理的,从而采用离散域设计。因此,本文建立了峰值电流模式控制数字移相全桥变换器环路模型,如图2所示。 图中,Gc(z)为电压环补偿函数,Hd(z)为 DSP 采样延时和输出误差延时,ZOH为数字处理与模拟电路之间的零阶保持器,Fm为斜坡补偿,He为反映峰值电流模式控制下电流环采样特性的函数。对于DSP而言,ADC采样和DAC变换的比例分别为1/3.3和 3.3。
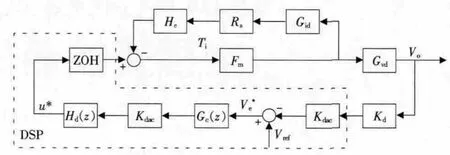
图2 数字移相全桥变换器控制环路框图Fig.2 Block diagram of digital phase-shift full-bridge converter control loop
2.1 斜坡补偿量对系统稳定性影响分析
峰值电流模式控制下的电流环框图如图2中的Ti。关于峰值电流模式控制电流环小信号模型的推导分析,文献[6]给出了为表征峰值电流模式的次谐波振荡现象而引入的He(s)传递函数,即

式中,Tw为电流环工作周期。考虑到移相全桥系统的工作频率是开关频率的2倍,则Ts=2Tw。式(3)说明当采用峰值电流模式控制时,除了采样电阻等造成的增益之外,自身的电流采样过程是存在增益和相移的。这也解释了不加斜坡补偿时次谐波振荡发生的原因。
比较外环输出的误差信号与采样电流,得到占空比的小信号增益传递函数为

为了消除当占空比大于0.5时出现的次谐波振荡现象,必须对电流环进行斜坡补偿。为了分析方便,以mc作为斜坡补偿量,则电流环开环传递函数Ti满足Ti=RsFmGidHe,可以得出

式(5)揭示了一个很重要的特性,即电流环与电流采样电阻是无关的,也即实际中采样增益不影响电流环的稳定特性。以mc为变量,伯德图如图3所示。
可以看出,首先是1/2工作频率点之前,Ti体现出的是二阶系统特性,在谐振频率点开始转折,1/2工作频率点之后,增益开始增加上扬,这是He影响导致。当不加斜坡补偿时,mc=1,增益曲线都大于0,系统不稳定;增大mc,相位裕度和增益裕量增大,系统进入稳定状态;当mc较大时,相角裕度也较大,这容易导致系统动态性能变差。通常斜坡补偿值的经验取值是输出滤波电感电流的下降斜率,即mc=2.286,由伯德图可以说明,经验取值下电流环是稳定的,本文所有涉及到mc为常量的取值都是此经验值。

图3 不同mc时电流环伯德图Fig.3 Bode plot of current loop with difference mc
对于整个系统,不考虑延时、ZOH和电压环补偿,则开环传递函数可表示为Gi=KdFmGvd/(1+Ti),伯德图如图4所示。当未加斜坡补偿时,400×103rad/sec处,即是1/2工作频率点,相位上爬,增益下降,说明开环传递函数分母存在两个右半平面极点,系统不稳定。增加补偿量,相位裕度增加,增益曲线下移。随着mc值增大,转折频率前移,相位下降点向前变化,下降斜率增大,这说明了:增加斜坡补偿后,右半平面的2个极点向左半平面移动,随着补偿的加大,这两个极点会向两端移动,一个极点向输出LC滤波的谐振点靠近,另一极点则远大于1/2工作频率。
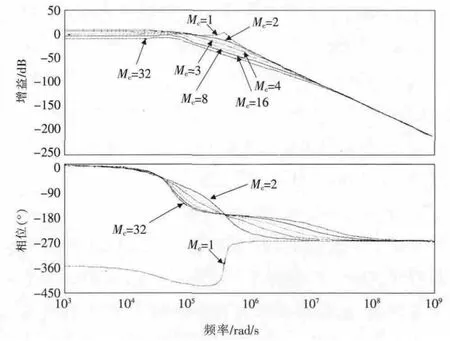
图4 双环下斜坡补偿对系统影响Fig.4 Effects of slope compensation in double-loop
2.2 谐振电感对系统环路稳定性影响分析
移相全桥区别于普通的Buck型电路其中之一是谐振电感的利用。然而,在实际中,谐振电感Lr不仅包括了缠绕的辅助谐振电感,而且包括了变压器的漏感。而变压器的漏感是无法一致的,因此,很有必要分析谐振电感对整个控制环路稳定性的影响。
考虑到Lr只与Rd相关,因此,将Rd作为变量,不考虑延时和补偿函数,则离散域系统的开环传递函数可以表示为
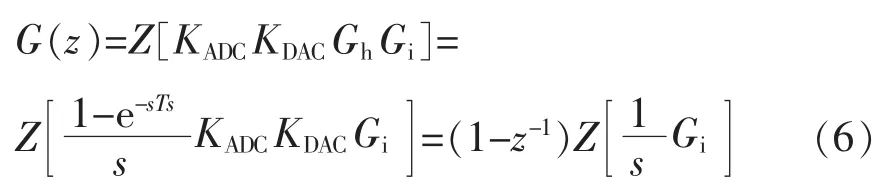

图5 Lr为7μH和21μH时系统根轨迹Fig.5 Root locus of system with Lris 7μH and 21μH
式中,Gh为零阶保持器的传递函数。其根轨迹如图5所示,其中虚线表示 Lr=7 μH,实线表示 Lr=21 μH,对于1+KG(z)=0,与单位圆交点分别对应K值2.73和3.12。根轨迹单位圆内都是系统稳定的区域,这说明了当谐振电感增大后,稳定范围变大,系统稳定带宽变宽,即表示抗环路的增益扰动能力增强。但是,谐振电感的加大使得占空比丢失严重。因此,选择合适的谐振电感非常重要。
2.3 延时对系统稳定性的影响
数字系统相较于模拟系统,一个突出的特征就是存在延时。移相全桥在数字处理时,延时了1个开关周期,也就是e-sTs,转化为离散域,那么延时可以表示成[7]z-1,因此,在考虑系统延时后,不包括补偿网络,那么,离散域系统开环的传递函数为
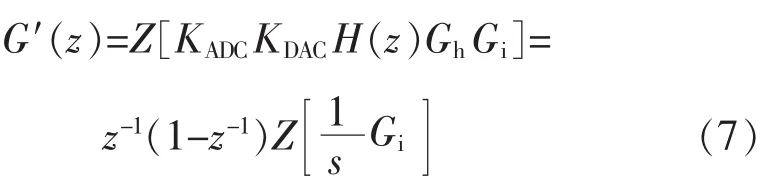
根轨迹图如图6所示。选取单位圆与根轨迹相交的临界点。当加入延时之后,当K<0.83时,根轨迹均处于单位圆内,系统稳定;与之相比,在不加延时情况下,K<2.73是系统稳定的范围。这说明,在系统加入延时之后,很明显的结果是边界K值减小了,也就是说系统的带宽变窄,延时导致了系统抗环路干扰能力的减弱。另外,在不加补偿时,原系统K=1>0.83,所对应的根轨迹不在单位圆内,系统不稳定。因此,在数字控制电路中,不同于模拟电路,延时的引入降低了系统的抗干扰能力,在实际设计中要对其加以特别的考虑。

图6 考虑延时后系统的根轨迹Fig.6 Root locus of considered delay time
2.4 系统补偿网络设计
数字控制电路的补偿网络设计必须考虑延时因素,从根轨迹可以看出,未加补偿时原系统是不稳定的。本文采用的补偿函数为PI补偿,借助Matlab SISO design tool,设计出的补偿函数为
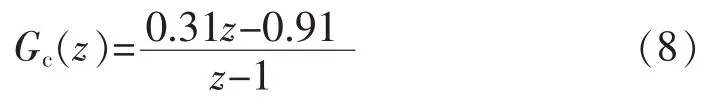
补偿后系统的伯德图如图7所示。穿越频率为2.15×104rad/s,即约为采样频率的 1/20,相角裕度为67°,增益裕量为8.4 dB,这说明所设计参数对系统具有良好的稳定性能。
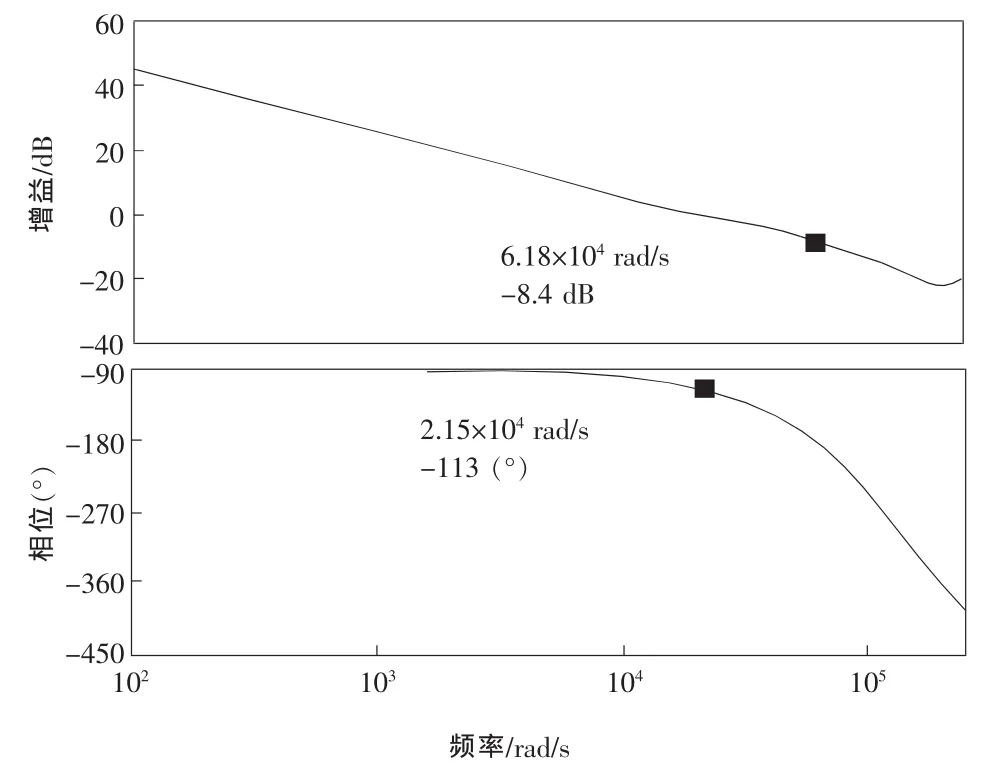
图7 补偿后系统的伯德图Fig.7 Bode plot of system after compensation
数字重设计是指连续域下设计出补偿函数,再变换为离散域进行数字处理;改进型数字重设计则在补偿函数设计时考虑了延时的影响。对延时采用Pade 二阶近似,PI系数可表示为:Kp=0.25,Ki=7.8×103。改进型数字重设计方法的伯德图如图8所示。与数字直接设计相比,两者穿越频率一致,但相角裕度和增益裕量分别增大了12°和2.9 dB,这是由于数字重设计模型中不存在零阶保持器所导致。因此,2种设计方法之间存在着差异,工程上要特别注意。

图8 改进型数字重设计的系统伯德图Fig.8 Bode plot of improved digital redesign system
3 实验结果与分析
表1 给出了本文使用到的基本变量参数。

表1 本文使用到的基本变量参数Tab.1 The variable parameters in the paper
图9 给出了输入电压300 V、输出电压13.5 V/150 A时变压器的原边电流、输出电压波形和对管的驱动波形。由图可以看出,电路运行状态良好。这说明所建立的峰值电流模式控制数字移相全桥变换器离散域模型和所设计出的斜坡补偿值和电压环补偿函数的正确性。
对系统做动态测试。当输入电压300 V时,在输出电流42 A和112 A间以50 Hz频率相互切载。图10给出了动态响应。切载时,纹波变化的主要由电容ESR导致。由图可以看出,切载过程导致输出电压变化,到调整为稳定所用的时间很短,切载过程只有1个尖峰并且最大波动值为490 mV,未出现多次振荡过程,体现了系统环路良好的动态性能。

图9 满载时电路主要波形Fig.9 Main waveforms in full-load
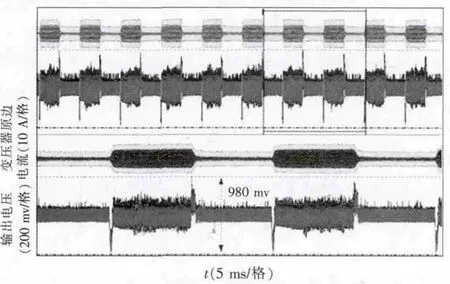
图10 切载时动态响应波形Fig.10 Waveforms of dynamic response in load variation
4 结语
本文建立了数字控制峰值电流模式下移相全桥变换器的离散域模型。分析了斜坡补偿的加大,有利于系统的稳定,但过大的补偿会使系统的动态性能变差。同时,漏感的增加可以使系统稳定带宽变宽,但会导致占空比丢失严重。数字控制延时的引入对数字移相全桥系统稳定性的影响较大,降低了系统的抗干扰能力。基于模型,使用直接数字设计方法设计系统补偿函数,对比改进型的数字重设计方法,其结果更准确。最后,实验结果验证了模型和理论分析的准确性。
[1]George N, Panchalai V N, Sebastian E, et al,Digital voltage-mode-control of a full-bridge phase-shift-modu-lated DC-DC converter.2014 Annual International Conference on,2014,7(2):1-6.
[2]Kim T H,Lee S J,Choi W.Design and control of the phase shift full bridge converter for the on-board battery charger of electric forklifts[J].Journal of Power Electronics,2012,12(1):113-119.
[3]吴红雪,杨威,杨世彦.基于TMS320F28027的数字控制移相全桥 DC/DC 变换器设计[J].电源学报,2012,10(4):24-28.Wu Hongxue,Yang Wei,Yang Shiyan.Design of phaseshifted full-bridge DC/DC converter based on digital control with TMS320F28027[J].Journal of Power Supply,2012,10(4):24-28(in Chinese).
[4]Tan F D,Middlebrook R D.A unified model for currentprogrammed converter.IEEE Transactions on Power Electronics,1995,10(4):397-408.
[5]Yadav G N B,Narasamma N L.An Active Soft Switched Phase-Shifted Full-Bridge DC-DC Converter:Analysis,modeling,design and Implementation[C].Power Electronics,IEEE Transactions on,Power Electronics,2014,9(29):4538-4550.
[6]Ridley R B.A new,continuous-time model for currentmode control.IEEE Transactions on Power Electronics,1991,6(2):271-280.
[7]Buso S,Mattavelli P.Digital control in power electronics.Lectures on Power Electronics,2006,1(1):59-61.
