一种新型Quasi-Z源逆变器及并网应用研究
2015-12-28刘海利庄圣贤郭允丰李矫鹏
刘海利,庄圣贤,郭允丰,李矫鹏
(1.西南交通大学电气工程学院,成都 610031;2.首钢京唐钢铁联合有限公司,唐山 063200)
引言
传统的电压型逆变器输出的交流电压峰值总是小于输入端的直流电压。因此,在输入电压较低或者变化范围较大时,如新能源发电系统,通常需要在其前级加入DC/DC升压电路,将直流电压升到足够大的值,以输出要求的交流电压,这不仅增加了系统的复杂性,而且降低了可靠性[3]。Z源阻抗网络的提出弥补了传统电压源逆变器的上述不足,然而传统的Z源逆变器存在着输入端电流断续,直流电压利用率低;器件应力过大,存在严重的启动冲击;升压能力有限的不足。针对这些不足,国内外学者展开了Z源逆变器拓扑优化方面的研究。文献[1]提出了电流连续型Quasi-Z源逆变器;文献[2]电容电压减小型Quasi-Z源逆变器;文献[4]提出在传统Quasi-Z源逆变器拓扑基础上,对拓扑结构进行改进,利用传统的Quasi-Z源逆变器模块的混联及串联,提出3种新拓扑,有效降低了电容电压,但升压比没有得到改善。
本文在文献[4]的启发下提出将 2个传统Quasi-Z源逆变器模块并联在直流源和逆变器之间,与传统的Quasi-Z源逆变器相比极大的减小了阻抗网络中的一个电容的电压,并且提高了升压比,降低了启动电感电流峰值。
1 传统的Quasi-Z源逆变器
图1 为传统的输入电流连续型Quasi-Z源逆变器拓扑结构。Quasi-Z源逆变器除了与传统的电压型逆变器一样存在8种开关矢量外,还多了一种直通零矢量状态,因此具有9中矢量即6种有效矢量、2种传统零矢量和1种直通零矢量。直通零矢量与零矢量一样,不会对输出电压产生影响。它是插入到传统零矢量中,是同一桥臂上、下开关管同时导通得到的。通过这个特有的直通零矢量达到升压目的。

图1 传统Quasi-Z源逆变器拓扑Fig.1 Topology of tranditional Quasi-Z source inventer
传统Quasi-Z源逆变器的直流侧的峰值电压Udc与直流电源电压 Uin之间的关系[1]为

式中:D0为直通占空比;B为逆变器的升压因子。由式(1)可知B大于等于1,从而实现了升压目的。则逆变器输出的相电压峰值可表示为

式中:M为调制因子。
由式(3)可知,逆变器的输出侧电压是由D0和M共同决定的,而且二者之间存在约束关系:M+D0≤1。可以看出D0不能无限制的增加,当D0增大时,M的调制范围会随之减小,而小的调制因子会对输出电压质量产生不良影响,限制了Quasi-Z源逆变器的升压能力。由式(1)可知当D0无限制地接近1/2时,逆变器直流端的峰值电压会越来越大,同时由式(2)可知:UC1、UC2上的电压也会越来越大,则对电容的耐压有更高的要求,这样就增加了电容的体积,降低了电路的可靠性,同时增加了电路的成本。
2 新型Quasi-Z源逆变器
2.1 电路拓扑及工作原理
新型Quasi-Z源逆变器拓扑见图2所示。图中,2个传统Quasi-Z源逆变器模块并联,使得电容UC2电压降低,输入侧电流连续,提高了Z源网络的升压能力。同时,高度的对称性有利于电路分析和参数选取。

图2 新型Quasi-Z源逆变器拓扑Fig.2 Topology of new Quasi-Z source inverter
新拓扑的工作原理类似于传统Z源逆变器,整个工作状态由直通和非直通2个工作状态组成,其等效电路如图3所示。为简化分析,假设所有器件均为理想状态, 并且 L1=L2=L3=L4=L,C1=C2=C3=C4=C。 在图 3(a)直通状态下,二极管 D1、D2被迫截止,电感 L1、L2、L3、L4储存能量; 电容 C1、C2、C3、C4释放能量,则可以得出此状态下的电路方程为


图3 新型Quasi-Z源逆变器的2种工作状态等效电路Fig.3 Two work state equivalent circuit of new Quasi-Z source inverter
在图3(b)非直通状态下,逆变器直流侧等效为一电流源,电压为Udc;此时二极管D1、D2导通,电感 L1、L2、L3、L4储释放能量。 电容 C1、C2、C3、C4存储能量。则此状态下的电路方程为
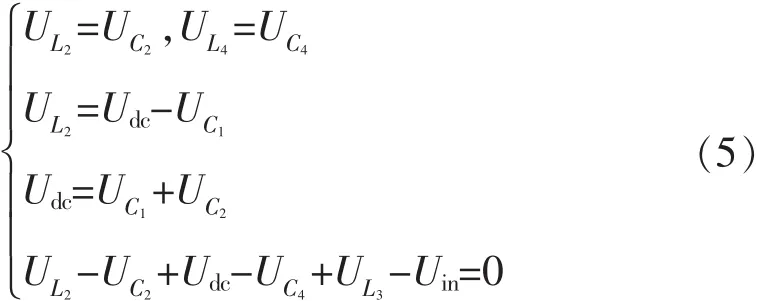

直流侧峰值电压与输入电压的关系为

式中:B为升压因子。当直通占空比D0≤1/3时,升压因子B大于等于1,从而实现了升压功能。
2.2 启动电感电流应力分析
在输入电压Uin和逆变器直流侧电压峰值Udc相同时,新型Quasi-Z源逆变器和传统Quasi-Z源逆变器的电感L1的电流如图4所示。由图对比可知新型Quasi-Z源逆变器启动电感电流的峰值小于传统Quasi-Z源逆变器。

图4 2种拓扑的电感电流对比Fig.4 Comparison of two topologies inductive current
2.3 Z源网络升压能力分析
阻抗网络的升压能力和逆变器的调制策略共同决定了Z源逆变器的升压能力。由式(1)和式(7)可知,在相同的直通占空比条件下,新型Quasi-Z源逆变器比Quasi-Z源逆变器具有更高的升压能力,如图5所示。
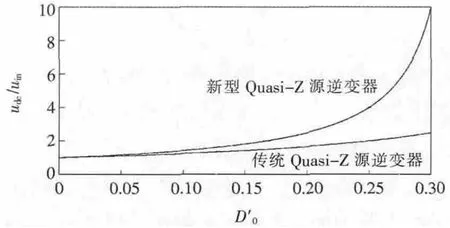
图5 2种拓扑在相同直通占空比下的升压能力对比Fig.5 Boot ability comparison of two topologies in same direct duty ratio
2.4 电容电压应力分析
文献[1]给出传统Quasi-Z源逆变器中Z网络电容电压应力为式(2)所示,由式(1)和(7)可知Quasi-Z源逆变器和新型Quasi-Z源逆变器的升压比不同,因此在分析他们的电容电压应力时需进行换算。在输入电压Uin和逆变器直流侧电压峰值Udc相同时,可得
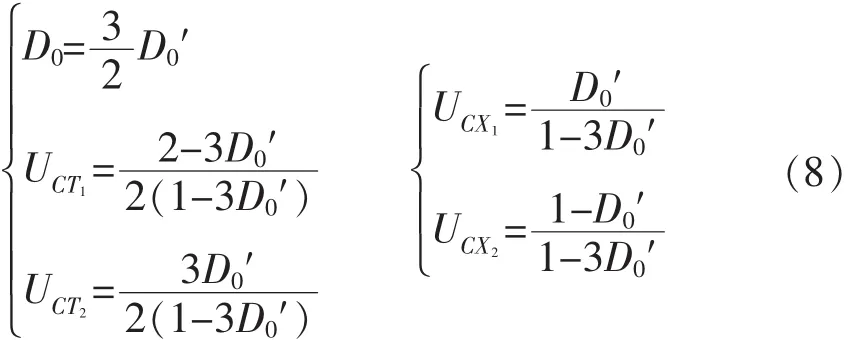
式中:D0′为新型Quasi-Z源逆变器的直通升压比;D0为传统源逆变器的直通升压比;UCT1、UCT2为换算过后的传统Quasi-Z源逆变器阻抗网络电容电压;为新型Quasi-Z源逆变器阻抗网络电容电压。由式(6)和式(8)得到Z源网络的电容电压与输入电压的比值UC/Udc和直通占空比D0′之间的关系曲线,如图6所示。

图6 两种拓扑结构的电容电压应力对比Fig.6 Capacitor voltage stress comparison of two topologies
由图6可知,在相同直通占空比条件下,对于对称结构中的电容,传统Quasi-Z源网络的UC2电容电压应力高于新型Quasi-Z的电容电压应力。而新型Quasi-Z源网络的UC1电容电压应力高于传统Quasi-Z的电容电压应力。
3 新型Quasi-Z源逆变器并网应用
由于采用SVPWM最大恒定升压调制策略进行调制,直通状态均在传统的零状态下加入,逆变器的输出决定于有效矢量。因此,逆变器的逆变桥到输出侧的分析完全与传统逆变器相同。文献[5]建立了三相逆变桥在dq旋转坐标系下的数学模型,即

式中:usd、usq分别为三相电网电压的直轴和交轴分量;分别为逆变器桥臂输出电压的直轴和交轴量分别为三相并网电流的直轴和交轴分量;ω为电网角频率;R为滤波电感的等效电阻。
由式(9)可知,直轴与交轴分量是相互耦合的,为了实现新型Quasi-Z源逆变器单位功率因数并网的要求,逆变器并网输出电流的q轴分量为0,其对d轴的影响可以不予考虑,而并网电流d轴分量耦合到交轴的分量,给电流控制器的设计带来难度。对式(9)进行解耦整理可得
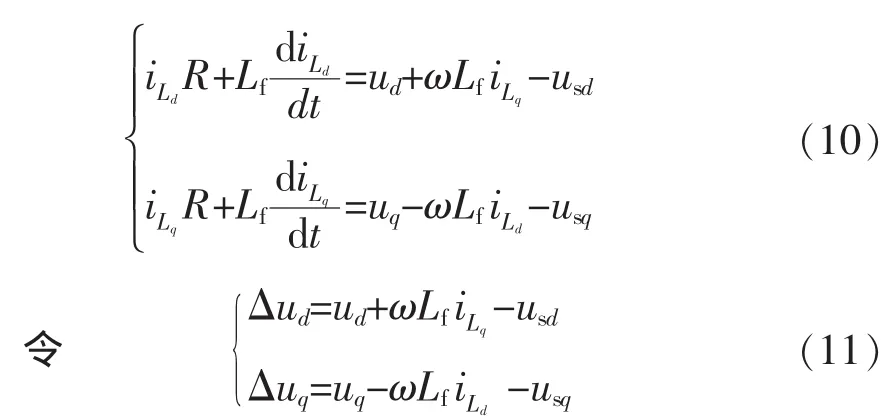
结合式(10)及式(11)可得

由式(12)可以看出,解耦之后,即在以Δud和Δuq作为电流等效控制变量时,直轴分量和交轴分量的并网电流是相互独立的,其等效控制变量可以由电流环PI控制器来决定,即
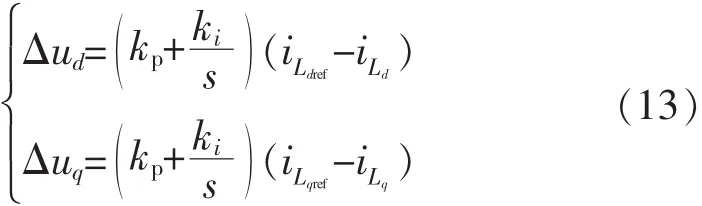
式中:kp、Ki为PI调节器的比例系数和积分时间常数,iLdref、iLqref分别为d轴和q轴的并网电流参考值
因此,可得
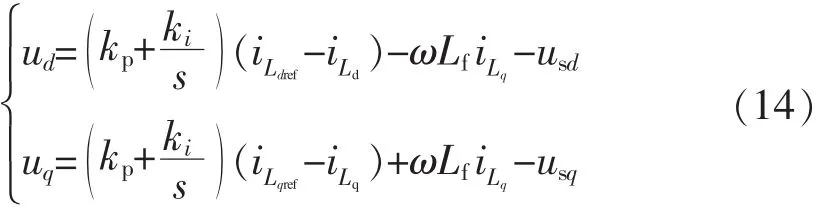
由以上推到可知,此时 d轴和q轴的控制量已相互独立,实现了并网电流的解耦。
对于新型Quasi-Z源逆变器,由于直流链电压Udc是脉动的电压,要想对其瞬时进行采样控制具有难度。因此,通常通过控制阻抗网络电容电压uC来间接控制直流链电压Udc的稳态。采用PI调节器来控制Udc的稳定,并获得直通占空比。
基于以上分析,建立的新型Quasi-Z源逆变器并网控制系统如图7所示。整个控制策略在dq坐标系下进行,整个控制系统分为2个闭环结构:并网电流控制电路和阻抗网络电容电压控制电路,其中并网电流控制电路以实现单位功率因数并网为控制目标。

图7 新型Quasi-Z源逆变器并网控制原理Fig.7 Principle of grid-connected control system of new Quasi-Z source inverter
4 仿真验证
4.1 开环电路性能仿真
为验证理论分析的正确性,对新型Quasi-Z源逆变器和传统Quasi-Z源逆变器进行对比仿真研究。
当直流电源电压Uin相同均为150 V,且直通占空比均为0.2时,新型Quasi-Z源逆变器和传统Quasi-Z源逆变器的直流母线电压Udc、交流侧相电压Ua和相电流ia的波形如图8所示。当直流电源电压Uin相同且均为150 V、直流母线电压Udc相同均为250 V时,新型Quasi-Z源逆变器和传统Quasi-Z源逆变器的阻抗网络电容电压的波形如图9所示。
对比图8和图9可得:在相同输入和相同直通占空比下,传统的Quasi-Z源逆变器直流母线电压为250 V,新型Quasi-Z源逆变器直流母线电压为375 V,与理论计算值相符,新型Quasi-Z源逆变器升压比增大;在相同输入和直流母线电压下,传统的Quasi-Z源逆变器阻抗网络电容电压Uc1=200 V,Uc2=50 V新型Quasi-Z源逆变器阻抗网络电容电压Uc1=216 V,Uc2=33 V。 与理论计算值相符,新型Quasi-Z源逆变器减小了一个电容电压。

图8 相同输入电压和D0下2种拓扑的波形Fig.8 Waveforms of two topologies in same input voltage and D0

图9 相同Uin和Udc下2种拓扑的波形Fig.9 Wareforms of two topologies in same Uinand Udc
4.2 并网仿真
并网仿真参数如表1所示。

表1 新型Quasi-Z源逆变器参数Tab.1 Parameters of new Quasi-Z source inverter
当直通占空比设为0.2、电网频率设为6 kW时,新型Quasi-Z源逆变器的直流母线电压、并网电压和电流的稳定波形如图10所示。

图10 并网稳态仿真波形Fig.10 Simulation waveforms of grid-connection steady state
0.35 s时输入电压突降40 V,直流母线电压Udc,输出三相交流电压uabc和三相电流iabc的仿真波形如图11所示。直流母线电压出现短期小幅的波动后迅速回复到800 V并维持稳定状态,而并网电流保持原状态不变,不受输入电流变化影响。由此可知,电容电压控制的直流母线电压闭环具有较好的稳定性。
0.3 s时,有功电流 idref由 12.9 A 增大至 16 A时,直流母线电压Udc,输出三相交流电压uabc和三相电流iabc的仿真波形如图12所示。由图可见,输出电流快速上升并保持稳定,表明在负载波动时,系统能够快速地做出调整,保证逆变器输出电压电流稳定。

图11 输入电压突变时的仿真波形Fig.11 Simulation waveforms when input voltage chops
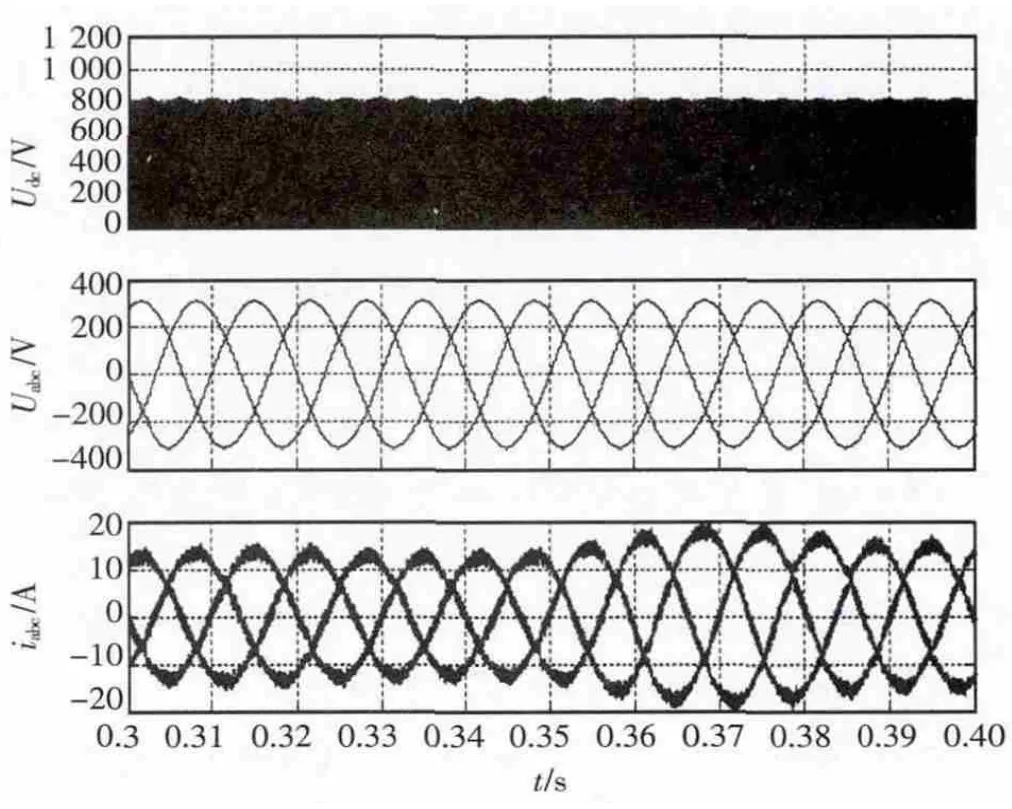
图12 并网电流突变时的仿真波形Fig.12 Simulation waveforms when grid current chops
5 结语
本文在Quasi-Z源逆变器的基础上提出一种新型Quasi-Z源逆变器拓扑,其输入侧电流连续,有效降低了阻抗网络中的一个电容的电压,并且提高了升压比,有效降低了器件的要求,提高了系统的可靠性。采用SVPWM最大恒定升压调制策略进行调制将该拓扑应用于三相并网系统,基于dq坐标系电流解耦及阻抗网络电容电压恒定的原理设计了控制。理论分析与仿真结果均验证了该结构模型的正确性和可行性。
[1]盛况,曲延滨,蔡春伟.准Z源逆变器SVPWM最大恒定升压调制策略研究[J].电气传动,2011,41(12):33-36.Sheng Kuang,Qu Yanbin,Cai Chunwei.Maximum constant boost control of Quasi-Z-source inverter based on SVPWM[J].Electric Drive,2011,41(12):33-36(in Chinese).
[2]蔡春伟,曲延滨,盛况.准Z源逆变器的暂态建模与分析[J].电机与控制学报,2011,15(10):7-13.Cai Chunwei,Qu Yanbin,Sheng Kuang.Transient modeling and analysis of Quasi-Z-source Inverter[J].Electric Machines and Control,2011,15(10):7-13(in Chinese).
[3]王利民,前照明,彭方正.Z源升压变换器[J].电气传动,2006,36(1):28-32.Wang Liming,Qian Zhaoming,Peng Fangzheng.Quasi-Z-source boost converter[J].Electric Drive,2006,36(1):28-32(in Chinese).
[4]汪成明,孙春霞,滕青芳.改进型 Quasi-Z源逆变器[J].电气传动,2013,43(8):38-43.Wang Chengming,Sun Chunxia, Teng Qingfang.Improved versions of Quasi-Z-source inverter[J].Electric Drive,2013,43(8):38-43(in Chinese).
[5]孙春霞,汪成明,滕青芳.一种改进型Quasi-Z源逆变器[J].兰州大学学报,2012,12(31):59-62.Sun Chunxia,Wang Chengming,Teng Qingfang.An improved versions of Quasi-Z-source inverter[J].Journal of Lanzhou Jiaotng University,2012,12(31):59-62(in Chinese).
[6]李红新,周林,郭珂,等.Z源逆变器最新进展及应用研究[J].电源技术,2013,137(3):504-508.Li Hongxin,Zhou Lin,Guo Ke,et al.Progress of Z-source inductor latest progress and its application development[J].Chinese Journal of Power Sources,2013,137 (3):504-508(in Chinese)
[7]邓凯,梅军,郑建勇,等.改进型开关电感准Z源逆变器[J].电网技术,2013,37(11)3254-3258.Deng Kai,MeiJun,Zheng Jianyong,etal.Improved switched-inductor Quasi-Z-source inverter[J].Power System Technology,2013,37(11)3254-3258(in Chinese)
[8]刘孝辉,郑建勇,尤鋆,等.开关电感型Quasi-Z源逆变器[J].电力自动化,2011,31(9)65-68.Liu Xiaojun,Zheng Jianyong,You Jun,et al.Switched-inductor Quasi-Z-source inverter[J].Electric Power Automation Equipment,2011,31(9)65-68(in Chinese)
[9]蔡春伟,曲延滨,盛况.增强型Z源逆变器[J].中国电机工程学报,2011,31(SI):259-266.Cai Chunwei,Qu Yanbin,Sheng Kuang.Enhanced Quasi-Z-source inverter[J].Proceedings of the CSEE,2011,31(SI):259-266(in Chinese)
[10]吴晓迪,梁占红,陶瑞.开关电感型Quasi-Z源逆变器SVPWM调制策略仿真研究[J].电源技术,2014,138(5): 925-929.Wu Xiaodi,Liang Zhanhong,Tao Rui.Simulation study of switched-inductor Quasi-Z-source inverter SVPWM modulating strategy[J].Chinese Journal of Power Sources,2014,138(5): 925-929(in Chinese)
[11]盛况.延展型Z源逆变器建模与调制策略研究[D].哈尔滨:哈尔滨工业大学,2011.Sheng Kuang.Research on Modeling and modulating strategy of extend Quasi-Z-source inverter[D].Harbin:Harbing Institute of Technology,2011(in Chinese)
