基于等效磁荷理论的磁力驱动器磁场计算

王春艳，李玉福

(1.长春师范大学计算机科学与技术学院，吉林长春130032;2.长春水务集团有限责任公司，吉林长春130012)

磁力驱动器利用永磁材料或电磁铁所产生的磁力作用，来实现力或转矩无接触传递。盘式磁力驱动器的主动磁环和从动磁环之间由金属隔离盘隔开，从而实现了液体无泄漏输送，其广泛地应用于磁力驱动泵、磁力驱动搅拌反应釜及磁力驱动控制器等设备中［1］。在优化磁力驱动器设计中，磁场分析与计算、涡流发热是两类需要解决的关键性问题。而磁力驱动器的磁场分布是影响隔离套中涡流的主要原因，解决涡流发热问题的前提是正确分析并计算磁场分布。目前常用的方法是基于磁路设计的基本原理，采用ANSYS软件，对磁场进行数值计算［2－4］。这种方法使用方便，但软件的有限元计算本身存在一定误差，采用不同的计算公式也是出现误差的重要原因，并且软件自带的网格划分无法进行磁场瞬态分析。本文以盘式磁力驱动器为研究对象，基于等效磁荷理论对气隙磁场分布进行分析，建立起气隙磁场数学模型，分析各主要结构参数对磁场的影响，提出一种新的基于时间划分网格的磁场分析方法。

1 盘式磁力驱动器结构与基本理论

1.1 盘式磁力驱动器基本结构

按照结构形式，磁力驱动器可分为圆筒式和圆盘式，盘式结构如图1所示。在图1中，1为主动磁环，2为隔离盘，3为从动磁环。

为方便计算，假设隔离盘的厚度远远小于其径向长度，这样可以忽略端部效应，近似认为磁场沿轴向没有变化，把三维问题转化为二维问题进行处理;忽略隔离盘因被交替磁化而在其内部产生的涡流磁场;假设永磁体沿轴向均匀磁化［5］。

1.2 基本公式

盘式磁力驱动器由主动磁环、隔离盘和从动磁环组成。为了研究磁感应强度与各位置参数之间的关系，建立圆柱坐标系和笛卡尔坐标系，分别来描述永磁体源点与待求场点的位置及待求场点磁感应强度的方向，如图2所示。

图1 盘式磁力驱动器结构

图2 盘式磁力驱动器坐标系

按照磁的库仑定律［6］，隔离盘上任意一点A处的磁感应强度为

用同样的方法，分别可以得到主动磁环M块永磁体外表面和从动磁环M块永磁体内、外表面在A点产生的磁感应强度。A点处总磁感应强度为

2 基于时间划分网格的磁场分析

当主、从动磁环转动时，隔离盘处于交变磁场中，该磁场的磁感应强度随时间规律性变化，以转过两个磁极所需要的时间为一个周期。在对时变磁场进行求解时，将磁感应强度与时间建立关系。

(ⅰ)由于磁环从开始转动到稳定这段时间很短，可以忽略因从动环速度慢而产生的转角差，即t0时刻起转角差为。以磁块一边作x轴。两个磁环的转角差，时间tx极小。

(ⅲ)在主动磁环上，关于时间划分时取相同间隔，把tn平均分成n份。即t1= Δt，t2=2Δt，…，tn=nΔt，由此得到 α1= ω1Δt，α2=2ω1Δt，αn=nω1Δt。m 个磁块在 A 点所产生的磁感应强度为

其中，有关参数说明如下:

i——控制磁环上的块数;

j——控制磁块的转动，随时间的变化;

k——控制隔离盘上沿径向等分数;

l——控制隔离盘上沿周向等分数;

Δt——对应转过一个磁块圆心角所用时间分的最小计算间隔。

同样方法，可以得出主动磁环永磁体外表面、从动磁环永磁体内表面和外表面所产生的磁感应强度。并由此计算磁感应强度总和如下:

Bx=Bnc1－x+Bnc2－x+Bwc1－x+Bwc2－x，

By=Bnc1－y+Bnc2－y+Bwc1－y+Bwc2－y，

Bz=Bnc1－z+Bnc2－z+Bwc1－z+Bwc2－z.

3 实验研究

以一个12极盘式磁力驱动器为例，用上述方法计算磁场及磁转矩。该磁力驱动器的参数见表1和表2。

表1 磁环几何参数

表2 隔离盘参数

3.1 磁场分析

在计算时，将隔离盘沿径向50等分，周向120等分。根据表1和表2中的数据，得出磁场分布结果如图3、图4所示。

图3 磁场与角度关系曲线

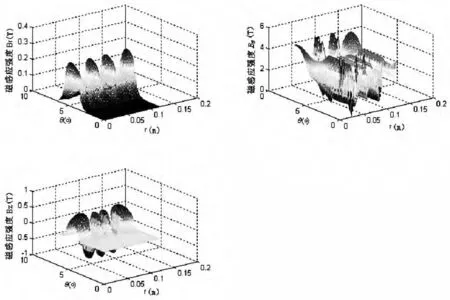
图4 磁场随隔离盘半径变化

对于不同时间参数，以两个磁极为一个周期，一个周期内的轴向磁感应强度变化曲线如图3所示。当主、从磁环相对转角逐渐增大时，磁感应强度向磁环转动方向偏移。形状呈近似正弦波，且在同一个周期内呈不严格奇对称。对于磁感应强度B=B(r，θ，t)，当t一定时，B关于(r，θ)的曲面形状基本一致，只是大小上有区别，由此在进行求解时可先给定t值，拟合出B=B(r，θ)。

3.2 磁转矩分析

只改变磁力驱动器磁极数，得到磁转矩与磁极数关系曲线，如图5所示。可以看出，磁极数对转矩影响较大。在一定范围内，磁转矩随着磁极数的增加而增大，说明磁极数多有利于转矩的传递。但磁极数目也不能过多，否则转矩会越来越减少。这是因为磁极数过多，漏磁增多，使得气隙中的磁通密度减小，传递的转矩降低。本文中磁力驱动器选择12极。

图5 磁转矩与磁极数关系

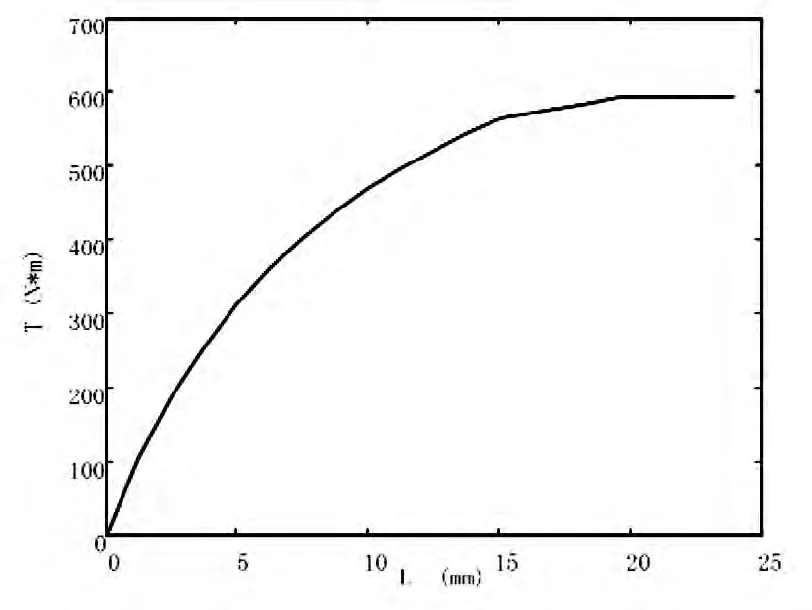
图6 磁转矩与磁块厚度关系

保持磁力驱动器其他参数不变，只改变从动磁环磁块的厚度，得到转矩与磁块厚度的关系，如图6所示。在一定范围内，磁转矩随磁块厚度迅速增加，当磁块厚度增加到一定值时，磁转矩增加缓慢，甚至基本不再变化。这是因为随着从动磁环磁块厚度的增加、磁势增加的同时，磁阻也增加，气隙中的磁通密度减小，造成转矩变小，所以实际应用中磁块的厚度不宜过厚。

保持其他尺寸不变，只改变气隙厚度大小，得到磁转矩随气隙厚度变化的曲线，如图7所示。转矩随气隙厚度的增加而迅速减小。由于磁环作为磁源，气隙中的磁阻要比主、从动磁环中的磁阻大得多，磁势主要消耗在气隙中，气隙厚度大，造成气隙中的磁通密度减小，从而导致磁转矩降低。

4 结语

综上所述，通过对基于等效磁荷理论的盘式磁力驱动器磁场的分析，建立起磁感应强度与隔离盘半径及角度参数之间的数学模型。采用对转角差划分和对时间参数划分的方法进行计算得出磁场分布情况，可以直观地观察磁力驱动器中磁感应强度的分布状况和隔离盘结构参数对磁场的影响。本文所做工作是进一步研究盘式磁力驱动器涡流发热问题的基础，研究磁力驱动器的不同参数对输出转矩的影响规律，为平面式磁力驱动器的优化设计提供了依据。

图7 磁转矩与气隙厚度关系

［1］赵克中.磁力驱动技术与设备［M］.北京:化学工业出版社，2003.

［2］孔繁余，陈刚，曹卫东，等.磁力泵磁性联轴器的磁场数值计算［J］.机械工程学报，2006(11):213－218.

［3］孔繁余，张勇，邵飞，等.高速磁力泵隔离套的磁涡流损失［J］.农业工程学报，2012(1):61－65.

［4］张孝春.磁力泵磁力驱动仿真系统的研究［D］.镇江:江苏大学，2009.

［5］张清.圆盘式磁力驱动器的涡流分析［D］.长春:吉林大学，2006.

［6］赵凯华，陈熙谋.电磁学［M］.北京:高等教育出版社，2003.

［7］Wang Chun － yan，Tan Qing － chang.Analysis of Magnetic Field Distribution in Disc Magnetic Drivers［C］.2010 conference on energy sources and smart grids development，2010(12):397 －400.