基于粒计算优化的DCT车辆起步离合器模糊控制

孔慧芳， 徐 超， 鲍 伟， 尹良杰

（1.合肥工业大学 电气与自动化工程学院，安徽 合肥 230009；2.安徽江淮汽车股份有限公司技术中心，安徽 合肥 230601）

车辆起步过程中，离合器的控制具有非线性、时变、强耦合和难于建模的特点，且工况复杂，而控制要求做到寿命长、舒适性好，因此双离合器接合过程的控制是 DCT（dual－clutches transmission）起步控制的核心和难点［1］。传统控制方法需要建立离合器的精确模型，而模糊控制技术则不需要［2－3］，所以更适合于离合器的控制，该技术已成为国内外学者研究的热点。文献［4］采用模糊方法控制离合器压力，文献［5］采用模糊神经网络方法控制离合器接合速度，文献［6］采用基于FCMAC智能方法控制离合器压力等，都取得了满意的控制效果。但DCT起步模糊控制系统在综合考虑人、车、路诸多因素时，输入维数多，在语言变量值较多的情况下，易出现模糊规则数量暴增、冗余严重、推理时间增长等现象，不利于实际应用。粒计算可以从大量数据中分析、推理、挖掘隐含知识及规律，与模糊控制结合后，可提取、简化决策过程中的控制规则［7］，提高控制效率。

本文将模糊控制技术与粒计算相结合，提出了一种对模糊规则约简的方法，减少了起步过程离合器控制的模糊规则数量，在满足起步控制要求［8］的前提下，能有效提升控制的实时性。

1 基于粒计算优化的模糊控制

1.1 粒计算定义

定义1 高阶粒［9－11］。设S＝（U，A，V，f）为一个信息系统，已知基本粒G1＝（φ1，m（φ1））和G2＝（φ2，m（φ2）），通过合取联结词∧构成二元对G＝ （φ，m（φ））＝（φ1∧φ2，m（φ1∧φ2）），由阶数求取公式λ＝Num（φ）表示φ包含的合取联结项的个数。λ＝2的粒称为二阶粒，由信息系统S上的所有二阶粒组成的集合称为二阶粒库，类似可推及λ＝n时的n阶粒和n阶粒库，λ≥2的粒称为高阶粒。

定义2 规则覆盖度和置信度［9－11］。设S＝（U，C∪D，V，f）为一个决策信息系统，已知G1＝（φ，m（φ））、G2＝（ψ，m（ψ））分别为条件知识粒和决策知识粒，｜＊｜表示＊对象的个数，如｜m（φ）｜表示m（φ）对象的个数。邻域是基于Rough集划分理论的一个扩展［12］，使用它作为粒计算表达，假设粒G1、G2对应的决策规则的描述为φ→ψ，则定义该规则覆盖度与置信度的计算公式分别为：

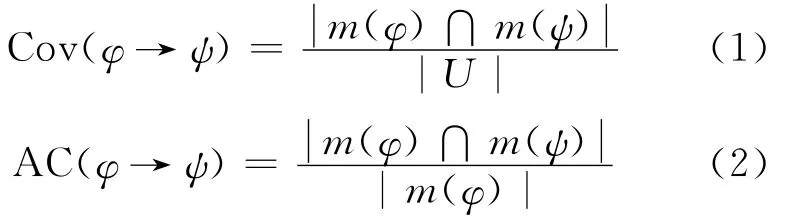
其中，（1）式反映决策规则φ→ψ对U中对象的覆盖程度；（2）式反映决策规则φ→ψ的确定性程度。

1.2 基于粒计算优化的模糊控制方法

基于粒计算优化的模糊控制方法主要由模糊规则的制定和规则约简2个部分组成。

模糊规则的制定可通过专家经验和工程知识、操作人员实际控制过程、自学习等方法实现。

根据粒计算理论，针对制定的模糊规则，引用不同粒度层次的简洁规则提取算法［8］，以规则覆盖度与置信度为启发信息，对大数量级的冗余模糊规则进行简化、优化，具体算法步骤如下。

输入：原始模糊规则表R＝（U，C∪D，V，f）。

输出：R的简化决策规则。

（1）根据条件属性集C、决策属性集D计算相应的条件基本粒库GC＝（φ，m（φ））和决策基本粒库GD＝（ψ，m（ψ））。

（2）计算GC中每个条件粒GCi对于决策粒GD1的覆盖度，获取知识粒库GR＝｛∀GRi＝（φi，m（φi））∈GC｜Cov（φi→ψ1）≥Cov0｝。

（3）对于GR中的每个粒GRi，计算其对于决策粒 GD1＝（ψ1，m（ψ1））的置信度 AC（φi→ψ1）。若 AC（φi→ψ1）≥AC0，则输出覆盖此决策粒GD1的决策规则φi→ψ1。

（4）将GR中规则未覆盖到且分属不同条件属性的条件粒合并成高阶粒，生成高阶粒库GCh，计算每个高阶粒G′i对于 GD1＝（ψ1，m（ψ1））的覆盖度Cov（Gi′），若 Cov（Gi′）≥Cov0且该高阶粒未被覆盖过，则转步骤（3）计算高阶粒对决策粒GD1＝（ψ1，m（ψ1））的置信度。逐步增加高阶粒的阶次，重复步骤（4），直至所有高阶粒均被覆盖。

（5）重复步骤（2）～（4）对决策粒库GD中的其余决策粒 GDi＝（ψi，m（ψi））进行规则提取。

（6）收集所有输出的决策规则，创建决策规则库。

将上述步骤提取的简化决策规则作为模糊控制器的规则，来控制系统的行为。

2 DCT起步过程模糊控制规则优化

粒计算优化的DCT车辆起步离合器模糊控制器的设计主要分为3个部分：模糊控制器结构及参数确定、起步控制规则制定、简化的决策规则获取。

2.1 DCT车辆起步模糊控制器结构及参数确定

本文通过控制离合器油压以控制离合器接合速度，实现车辆平稳快捷起步。基于复杂工况，选定2层模糊控制器，并设计了DCT车辆起步控制系统逻辑结构框图，如图1所示，其中，电磁阀电流计算模块由标定获得的电磁阀执行机构的P－I特性曲线表构成。

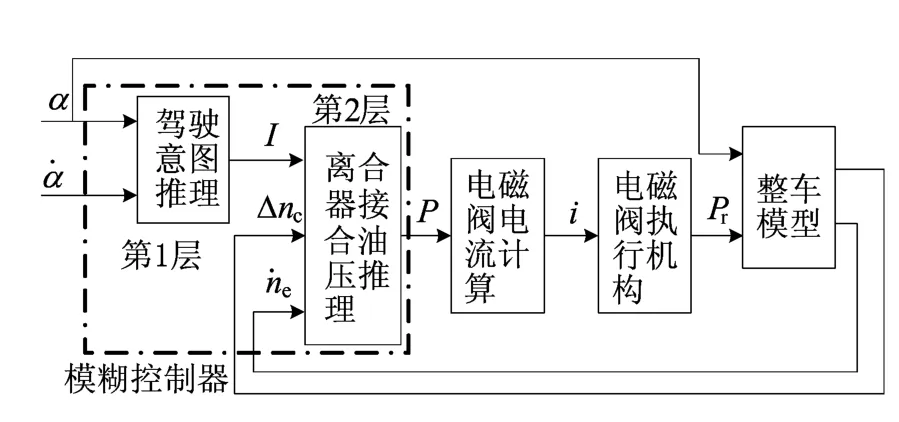
图1 DCT车辆起步控制系统逻辑结构框图

模糊控制器的第1层为驾驶意图推理，根据油门开度α及其变化率α˙推理出驾驶意图I；第2层为离合器接合油压推理，根据发动机转速变化率˙ne、离合器主从动盘转速差Δnc和驾驶意图I推理出离合器目标油压P；再由P经查P－I特性曲线表得电磁阀电流i和控制离合器实际油压Pr，Pr与α输入至整车模型后可以实时得到Δnc、˙ne，并反馈给模糊控制器。

模糊控制器的各输入输出变量的模糊语言集和论域定义见表1所列。

表1 模糊控制器各变量的模糊语言集和论域

2.2 DCT车辆起步模糊规则制定

根据驾驶员经验和专家知识，制定DCT起步模糊规则控制离合器油压，主要原则如下：① 通过油门踏板开度及其变化率识别驾驶意图，为离合器油压的确定提供依据；② 快起步时，要求在保证车辆不熄火前提下，尽量缩短起步时间；③ 慢起步和正常起步时，要求在保证车辆不熄火并满足相应冲击度的前提下，尽量减小滑摩功。

归纳制定第1层驾驶意图推理规则见表2所列，第2层离合器油压推理规则共有245条，篇幅所限，仅列出I＝VS时的规则，见表3所列。

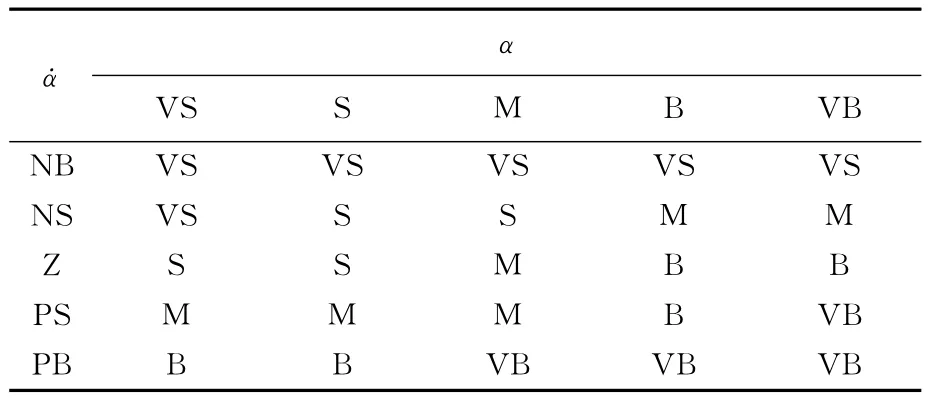
表2 驾驶意图I推理规则表

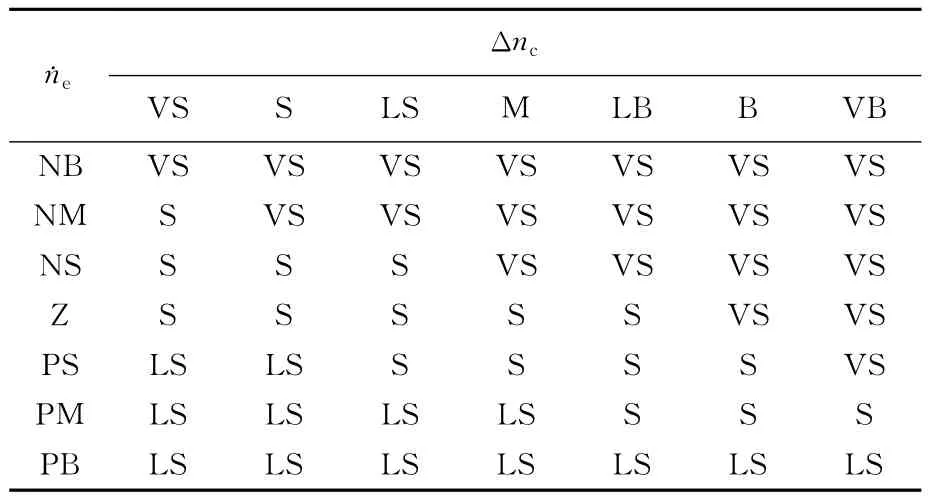
表3 I＝VS时DCT起步离合器油压P模糊规则表

2.3 DCT车辆起步的简化决策规则获取

对第2层离合器油压推理的245条规则进行简化，以表3为例进行规则简化说明：选择条件属性集C＝｛I，˙ne，Δnc｝、决策属性集D＝｛P｝，归纳得到条件基本粒库GKV＝ ｛I＝VS，˙ne＝NB，˙ne＝ NM，˙ne＝ NS，˙ne＝Z，˙ne＝ PS，˙ne＝ PM，˙ne＝PB，Δnc＝ VS，Δnc＝S，Δnc＝ LS，Δnc＝M，Δnc＝LB，Δnc＝B，Δnc＝ VB｝和决策粒库GD＝ ｛P＝VS，P＝S，P＝LS｝；根据1.2节中算法步骤进行规则的覆盖度和置信度计算，并选择Cov0＝1／49、AC0＝0.7对表3进行简化，获得的简化规则见表4所列。

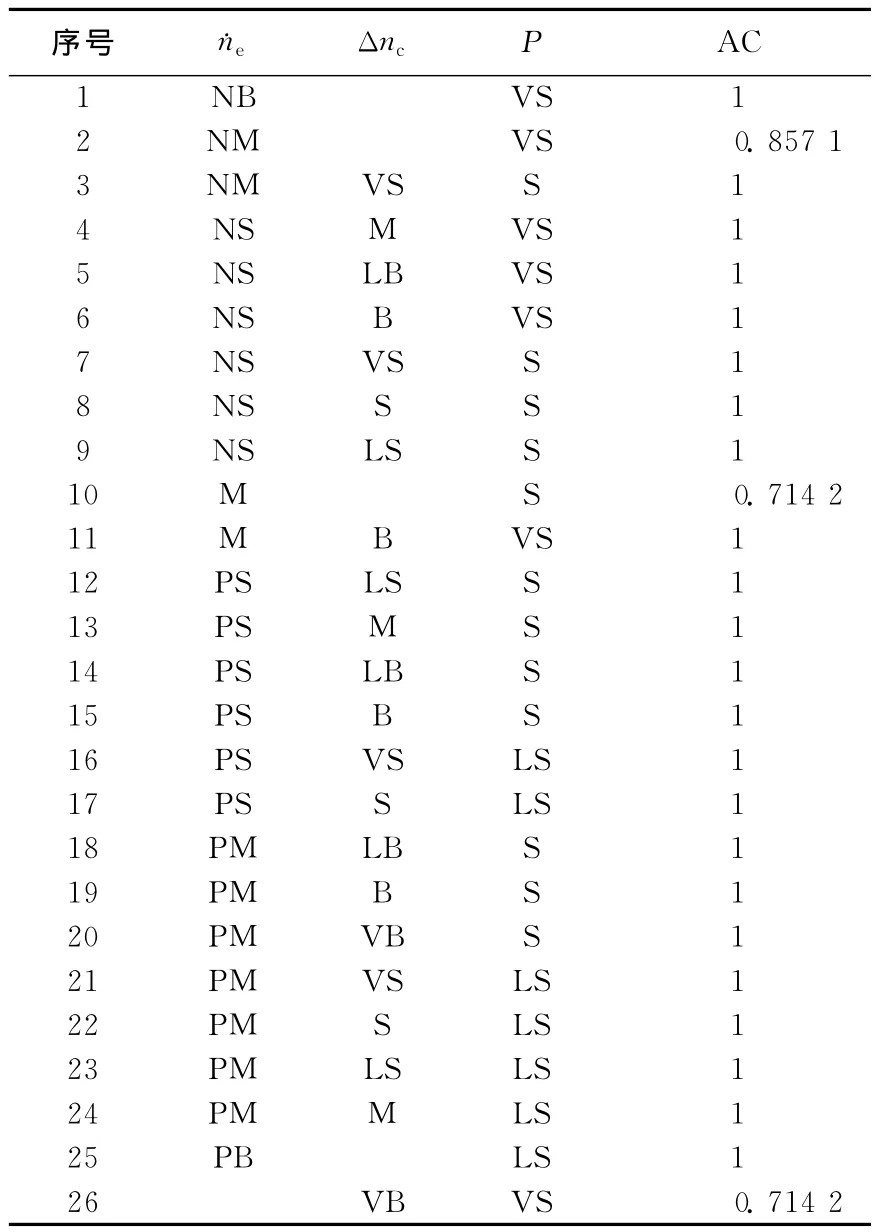
表4 I＝VS时DCT起步离合器油压P简化决策规则表

比较表3和表4可以看出，简化后模糊规则由49条减少为26条。

表4中规则1、2、10、25、26共覆盖表3中的32条规则，但其中包含置信度不为1的规则；表4中剩余21条规则对表3中未覆盖到的规则进行表述，并对置信度不为1的规则进行更细致的表述。综上可知，表4的26条规则实际已覆盖表3的49条规则，但规则数量减少，达到简化效果。选择Cov0＝1／245、AC0＝0.7，对第2层的245条模糊规则进行简化，最终得到145条置信度超过0.7的简化决策规则。

3 仿真分析

利用 Matlab／Simulink软件建立DCT车辆起步控制系统的仿真模型对DCT起步过程进行仿真。

DCT快起步和慢起步的仿真结果如图2所示。

图2中实线和虚线分别为未优化的和粒计算优化后的模糊规则下的仿真结果，其中图2a和图2d为离合器接合过程仿真曲线，图2b和图2e为冲击度仿真曲线，图2c和图2f为滑摩功［6］仿真曲线。

比较图2中各虚线与实线可知，两者均能满足平滑快捷的起步要求，且效果基本一致，具体指标及相应规则数由表5、表6列出。

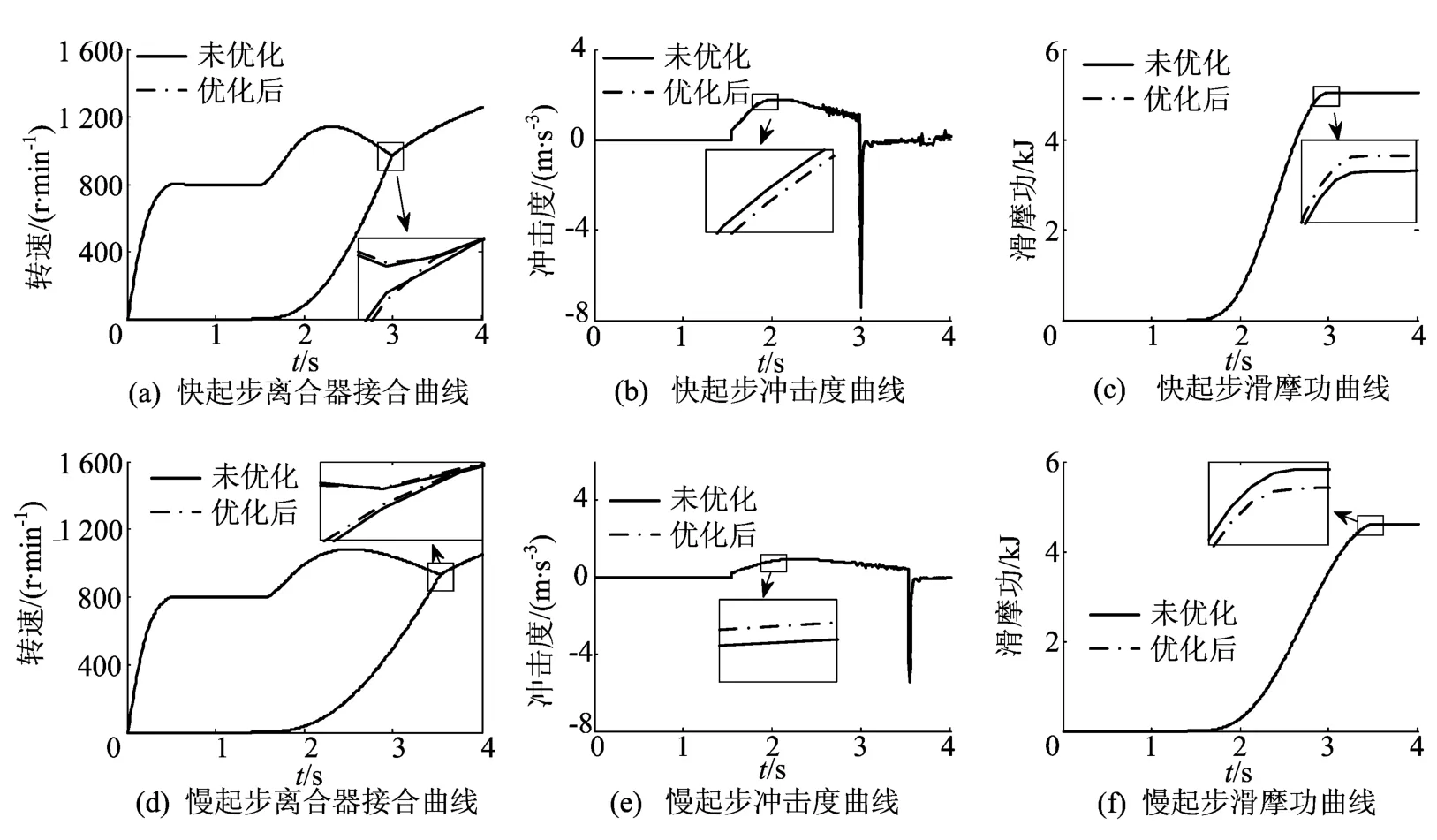
图2 粒计算优化前、后的模糊控制仿真结果对比图

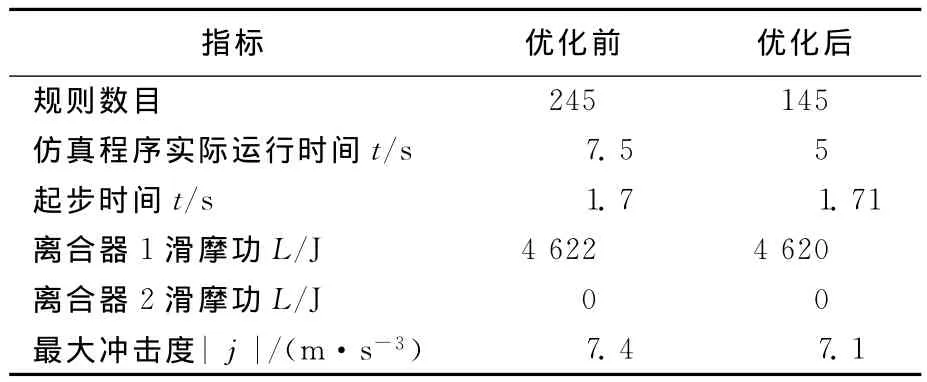
表5 快起步粒计算优化前、后的模糊控制仿真结果对比

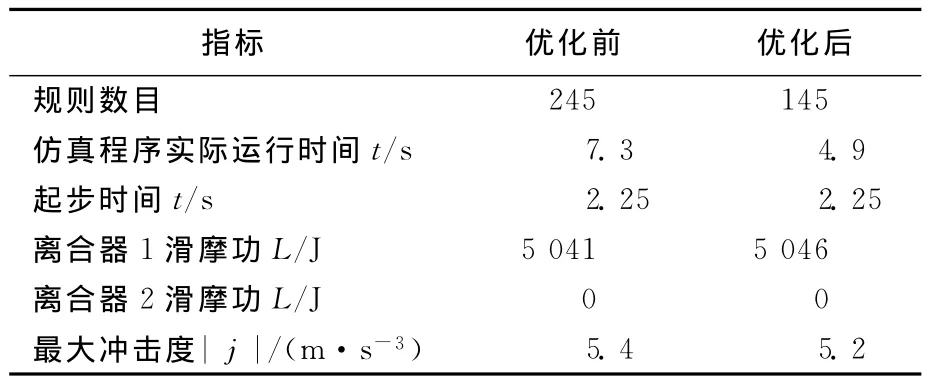
表6 慢起步粒计算优化前、后的模糊控制仿真结果对比

由表5和表6可知，同等工况、同等仿真条件下DCT车辆的起步品质指标在2种规则控制下基本保持不变，但基于粒计算优化后的模糊控制规则数目仅占未优化的模糊控制规则的60%，规则存储空间减小，仿真程序实际运行时间缩短，表明模糊推理时间缩短，控制系统效率提升。

综上可知，基于粒计算优化的模糊控制可以简化规则，并较好地控制离合器接合，实现DCT车辆平稳快捷起步。

4 结 论

（1）本文提出的基于粒计算优化的模糊控制方法为解决多输入、多语言变量的复杂结构下模糊规则指数增长、冗余严重且难以简化导致实际应用困难的问题提供了一种新思路。

（2）本文方法为DCT车辆起步离合器控制的一项新探索，仿真结果显示，基于粒计算优化的模糊控制减少了模糊规则、提升了控制效率，且基本不影响DCT车辆起步性能。

（3）本文方法中最小覆盖度与最小置信度的选取对规则的简化程度影响较大，选择不当可能对控制性能产生不利影响，需要进一步研究。

［1］ 张世义，李光辉.双离合器自动变速汽车起步模糊控制研究［J］.重庆交通大学学报：自然科学版，2009，28（4）：794－800.

［2］ Golea N，Golea A，Benmahammed K.Fuzzy model reference adaptive control［J］.IEEE Transactions on Fuzzy Systems，2002，10（4）：436－444.

［3］ Ren T J，Chen T C.A robust model reference fuzzy control for nonlinear systems［C］／／Proceedings of the 2004IEEE International Conference on Control Applications，Vol 1.IEEE，2004：165－170.

［4］ Kong H F，Li X P，Bao W.Control of clutch on DCT dur－ing start process［J］.Applied Mechanics and Materials，2012，130／131／132／133／134：357－360.

［5］ 吴光强，司建玉.双离合器自动变速器起步的智能控制策略［J］.同济大学学报：自然科学版，2012，40（1）：81－87.

［6］ 王印束，程秀生，冯 巍，等.湿式双离合器式自动变速器起步智能控制［J］.江苏大学学报：自然科学版，2011，32（6）：658－662.

［7］ 谢克明，陈泽华，谢 刚.粗糙集理论及其在智能控制中的新进展［J］.计算机科学，2004，31（10）：41－44.

［8］ 孔慧芳，任亚明.基于遗传算法优化的汽车起步模糊控制策略［J］.合肥工业大学学报：自然科学版，2009，32（1）：21－23.

［9］ 徐久成，史进玲，成万里.粒计算中决策规则的提取［J］.计算机工程与应用，2009，45（25）：132－134.

［10］ 李 娓.基于粗糙集的粒计算在数据挖掘中的研究与应用［D］.武汉：武汉理工大学，2011.

［11］ Pawlak Z.Rough sets and intelligent data analysis［J］.Information Science，2002，147（1）：l－12.

［12］ 王 蕊.基于粒计算的不完备决策系统数据挖掘研究［D］.成都：西南交通大学，2008.