冷作中用三角函数法提高做任意角的精度

■吉林市厦林化工分离机械工业有限公司 王鑫缘，曹红爱，李占文

在冷作中进行放样、成形、组装、检验及现场测绘等工序中，求做任意角是经常发生。当角边长较大、角度α为非30°、45°、60°特殊角度，或角度精度要求较高时，尤其所做角要求达到“分”、甚至“秒”的精度要求时，是一个棘手的问题。本文介绍一种采用三角函数计算法，通过长度度量的量具来求做角的方法，不仅方便易行，且可以显著改善上述存在的问题难度。尤其当角度为任意值时，更有实用价值。

1. 基本做法

（1）正切法 当所求角度为α，其做法如下：做一确定长度线段AB，长度自定，但宜大不宜小（一般可采用1000～2000mm）（见图1)。做BP⊥AB，在BP上截取r=BC=ABtanα，得C点。连接AC，则角∠BAC即为所求角α。

（2）正弦法 当所求角度为α，其做法为：画一以直径AO=OB=2r，O为圆心的弧 (AB=1000～2000mm即可)（见图2）。 以B点为圆心，以r=ABsinα为半径，在⊙O的半圆弧上截得C点。连接AC、BC，则角∠BAC即为所求的角α。

图1 正切法求做一角

图2 正弦法求做一角

2. 示例

正切法做∠α=33°25'37"为例，做法为：采用CADIO型（牌）计算器查阅tan33°25'37"=tan33.426945°=0.660053466取AB=1000mm，则

且BC⊥AB。连接AC，则角∠BAC即为所求的角α。

3. 精度分析

一般情况下，冷作下料采用粉线和滑石笔划线时，将尺寸偏差精度有效控制在±2mm内是能够稳定实现。当采用划针时，其精度偏差可控制在小于±0.5mm范围内。

本文按冷作实际划线操作保证误差精度，能够稳定控制在±2mm范围内，以所画最长边长AB=1000mm，BC=600mm时为例进行误差分析。

（1）最大负偏差分析 以上述示例采用正切法做角为例：当三角形底边AB实际长度偏差为+2mm，直角边BC长度为负偏差-2mm时，角α显然处于负偏差范围内，且处于最大负偏差之处，其偏差值

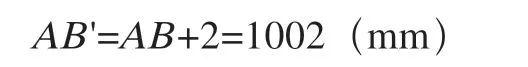
而当

（2）最大正偏差分析 AB' =AB-2=998（mm），而当时（见图4），显然其角度偏差处于正偏差范围内，且处于最大正偏差之处

对于最大角度90°＞α＞89°和最小角度0°＞α＜1°状态下的误差分析从略。

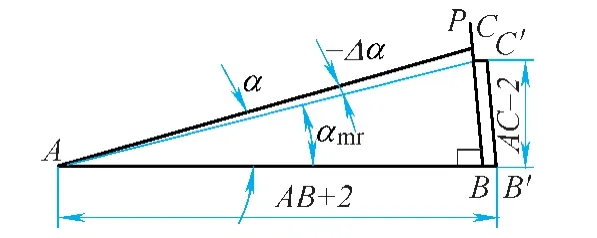
图3 最小负偏差角度

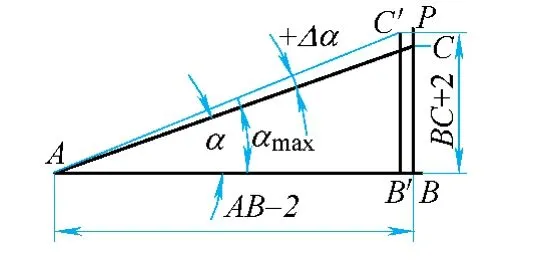
图4 最大负偏差角度

上述误差分析，对于一般要求其误差允许范围在±30'时，显然是能够完全充分满足验收要求的。如果需要提高所做角度精度，在保证所做角边长测量精度控制在±2mm时，可通过增加所做角边长来实现。因为当所选择角度底边AB长度增加与所做角度的精度呈正相关。