由6个相似压缩确定的自相似Cantor集的Hausdorff测度的准确值

许绍元

（韩山师范学院数学与统计学院，广东潮州 521041）

由6个相似压缩确定的自相似Cantor集的Hausdorff测度的准确值

许绍元

（韩山师范学院数学与统计学院，广东潮州 521041）

研究了一个由6个相似压缩确定的满足开集条件的自相似Cantor集，得到了它的Hausdorff测度的准确值.

自相似Cantor集；Hausdorff维数与Hausdorff测度；开集条件

1 引言与预备知识

众所周知，Hausdorff维数与Hausdorff测度是分形几何的理论基础，因此计算或估计分形集的Hausdorff维数与Hausdorff测度是十分重要的问题.一般来说，分形集的Hausdorff维数与Hausdorff测度计算或估计都十分困难，而计算分形的Hausdorff测度就更难了.至今为止，研究最成功的分形是满足开集条件的自相似集，它的Hausdorff维数等于自相似维数，其Hausdorff测度则是一个有限正数.但目前，就是对这么一个简单的分形，其Hausdorff测度的计算仍然十分困难.

近年来，许多学者试图计算自相似集的Hausdorff测度的准确值，并得到一些有用的结果（见文献[1-12]），其中文献[12]介绍的一种基本方法（见下文引理2.1）计算满足开集条件的自相似集的Hausdorff测度的准确值，并举例计算出由4个相似压缩构成的迭代函数系所确定自相似Cantor集的Hausdorff测度的准确值.本文同样采用这一方法，讨论了由六个相似压缩构成的迭代函数系所确定的自相似Cantor集，得到了它的Hausdorff测度的准确值.

一些基本概念、符号和已知结果见文献[9-12].

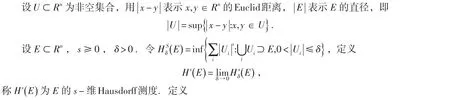
2 主要结果

首先，给出一个有用的引理.

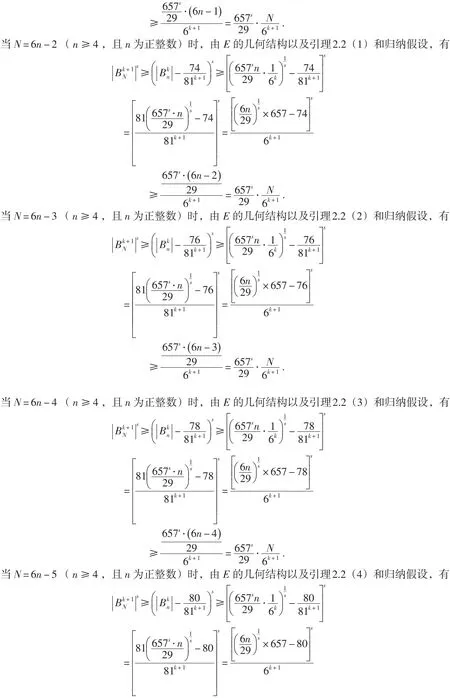
（致谢：衷心感谢审稿人仔细审阅原稿，并提出了宝贵的修改意见.）

[1]ZHOU Z，FENG L.Twelve Open Problems on the Exact Value of the Hausdorff Measure and on Topological Entropy:a Brief Survey of Recent Results[J].Nonlinearity，2004，17：493-502.

[2]MARION J.Mesures de Hausdorff D’ensembles Fractals[J].Ann.Sci.Math.Quebec，1987，11（1）：111-132.

[3]SRICHARTS R S.Exact Hausdorff Measure and Intervals of Maximum Density for Cantor Sets[J].Trans.Amer.Math.Soc.，1999，351（9）：3725-3741.

[4]WU M.The Hausdorff Measure of Some Sierpinski Carpets[J].Chaos，Solitons and Fractals，2005（24）：717-731.

[5]ZHOU Z.Hausdorff Measure of Self-Similar Set-the Koch Curve[J].Sci.China.（Ser.A）:1998，41（7）：723-728.

[6]ZHOU Z，FENG L.A New Estimate of the Hausdorff Measure of the Sierpinski Gasket[J].Nonlinearity，2000，13：479-491.

[7]ZHOU Z，WU M.The Hausdorff Measure of a Sierpinski Carpet[J].Sci.China，（Ser.A）,1999,29（2）：138-144（in Chinese）.

[8]ZHOU Z，WU M，Zhao Y.The Hausdorff Measure of a Class of Generalized Sierpinski Sponges[J].Chin.J.Contemp.Math.，2001，22：55-64.

[9]FALCONER K J.The Geometry of Fractal Set[M].Cambridge:Cambridge University Press，1985.

[10]FALCONER K J.Fractal Geometry-Mathematical Foundations and Applications[M].New York：John and Sons，1990.

[11]HUTCHINSON J E.Fractals and Self-similarity[J].Indiana Univ.Math.J.1981，30：713-747.

[12]许绍元，周作领，苏维宜.自相似集的质量分布原理与Hausdorff测度及其应用[J].数学学报，2010，53（1）: 117-124.

On the Exact Hausdorff Measure of a Self-similar Cantor Set Yielded by 6 Similarities

XU Shao-yuan
（School of Mathematics and Statistics,Hanshan Normal University,Chaozhou,Guangdong,521041）

In this paper,a self-similar Cantor set with the open set condition(OSC)yielded by 6 similarities is discussed and its exact Hausdorff measure is computed.

self-similar Cantor set；Hausdorff measure and dimension；open set condition

O 189.1

A

1007-6883（2015）06-0001-07

责任编辑 朱本华

2015-10-29

韩山师范学院创新强系项目（项目编号：2013）.

许绍元(1964-)，男，湖北武汉人，韩山师范学院数学与统计学院教授.