磨削弧区热源分布形状研究

王德祥,葛培琪,2,毕文波,郑传栋

(1.山东大学机械工程学院,250061,济南;2.山东大学高效洁净机械制造教育部重点实验室,250061,济南)



磨削弧区热源分布形状研究

王德祥1,葛培琪1,2,毕文波1,郑传栋1

(1.山东大学机械工程学院,250061,济南;2.山东大学高效洁净机械制造教育部重点实验室,250061,济南)

为了研究磨削力与磨削热耦合作用的残余应力场,基于磨粒轨迹分析和磨粒接触分析,采用概率统计的方法建立了磨削弧区热源分布模型。模型分析了磨削弧区热量分配关系,不需预先假设沿磨削弧总热源分布形状及热量分配比一致,即可获得磨削弧区热源分布形状,解决了以往热源分布形状常被假设为矩形和直角三角形,但矩形热源和直角三角形热源并不能准确地描述热源分布形状的问题。采用有限元法仿真分析了工件磨削温度场,采用热成像仪实测了磨削温度场,并将磨削温度场有限元仿真结果和热成像仪测量结果进行了对比分析,结果表明:有限元模拟结果与热成像仪测量结果具有很好的一致性,磨削弧区最高温度预测值与实测值之间的误差在2.24%～15.3%范围内;直角三角形热源并不能准确地描述磨削弧区热源分布形状;磨削弧区热源分布形状更接近四次多项式函数曲线。

热源分布;热源形状;热量分配比;磨削温度场

磨削加工需要极高的能量,几乎所有的能量都在磨削弧区转化为磨削热[1]。磨削加工时进入工件的磨削热会导致工件表层产生残余拉应力,从而降低被加工表面的疲劳寿命。工件表层的高温以及极大的温度梯度是产生残余拉应力的主要原因。热源分布形状是进入工件表面的热流密度分布,是分析磨削温度场的重要依据。一般把热源分布形状假设为矩形或直角三角形,磨削试验表明,直角三角形热源比矩形热源更加准确[2-4],文献[5]也认为三角形热源更加符合实际磨削工况。近年来,热源分布形状被假设为多项式曲线[6]、抛物线[7]和椭圆[8]等形状,利用试验测得的磨削温度场数据进行传热逆分析,可以获得热源分布形状[9-13],研究发现直角三角形并不是最准确的热源分布形状[13]。但是,根据试验结果反推热源分布形状的方法,对试验误差和随机误差很敏感,不便于工程应用。

如前所述,热源分布形状被假设为矩形、直角三角形或其他形状,但是这些假设都是基于特定的磨削条件,不能反映热源分布的真实形状。因此,本文基于磨粒轨迹和磨粒接触情况,分析了磨削弧区热量分配关系,研究了磨削弧区热源分布形状,建立了瞬态磨削温度场有限元模型,仿真分析了工件瞬态磨削温度场。

1 热源分布建模

图1为磨削弧区热源分布建模方案。首先,计算磨削接触弧长lc和最大未变形切屑厚度hcu,max,两模型参数主要用于磨粒轨迹分析。然后,进行磨粒轨迹分析和磨粒接触分析,计算磨削力。再根据磨削弧区切向磨削力分布,获得磨削弧区总热源分布。最后,分析磨削弧区热量分配关系,获得磨削弧区进入工件的热源分布形状。

图1 热源分布建模方案

1.1 磨削接触弧长

磨削接触弧长lc是磨削加工时砂轮与工件的真实接触弧长,它直接决定了热源的长度,而且在法向磨削力Fn的作用下,磨削弧区真实接触弧长lc比几何弧长lg大,因此需要确定lc。

在建立磨削弧区热源分布模型时,由于磨削力未知,将磨削弧区几何弧长lg作为lc的初始值。根据磨削原理,lg=(aeds)1/2,ae是磨削深度,ds是砂轮直径。在获得法向磨削力Fn后,再对lc和hcu,max进行修正,直到获得稳定的磨削接触弧长lc。本文采用的Rowe推导的磨削接触弧长公式[14]如下

(1)

式中:Rr是粗糙系数;b是磨削宽度;Ks是砂轮弹性模量;Kw是工件弹性模量。

1.2 磨削力求解

根据文献[15],通过磨粒轨迹分析和磨粒接触分析,获得最大未变形切屑厚度hcu,max。本文在磨削力求解过程中,通过磨粒轨迹分析,确定磨削弧区任意位置l处的磨粒接触类型,即滑擦、耕犁或切削。在磨粒接触分析的基础上,分别建立单颗滑擦磨粒、单颗耕犁磨粒和单颗切削磨粒的微观作用力模型。将磨削弧区均匀离散成n个子区域,每个子区域长度Δl=lc/n。针对每个子区域,结合磨粒轨迹分析结果与单颗磨粒作用力模型,求解磨削弧区任意位置l处的磨削力Fl,其法向分量和切向分量分别为Fnl和Ftl。累加Fl,即可获得磨削弧区总磨削力F,其法向分量和切向分量分别为Fn和Ft。Ftl用于获得磨削弧区总热源分布,Fn用于修正磨削接触弧长。

1.3 磨削弧区热量分配关系分析

准确描述砂轮表面形貌是分析热量分配关系的重要基础。根据文献[15],可以得到砂轮表面形貌的描述公式式(2)～式(4)。

(1)磨粒尺寸概率密度函数为

(2)

式中:x∈[-a,a];a=dmax-dmean,dmax是最大磨粒直径,dmean是平均磨粒直径,dmean=(dmax+dmin)/2,dmin是最小磨粒直径。

(2)磨粒突起高度概率密度函数为

(3)

式中:h是磨粒突起高度;ha是最高磨粒突起高度hmax与平均磨粒突起高度hmean之差,即ha=hmax-hmean,hmax和hmean在数值上分别等于dmax和dmean。

(3)磨削弧区任意位置l处的磨粒接触半径为

(4)

式中:h0是磨削弧区位置l处的最小磨粒突起高度,h0=hmax-hcu,maxl/lc;hcutx是磨粒切入深度,hcutx=h-hmin,hmin是磨削弧区与工件材料接触磨粒的最小突起高度。

磨削弧区总热源分布通过Ftl获得,表述为

(5)

式中:vs是砂轮速度;Ftl是磨削弧区任意位置l处的切向磨削力。

如图2所示,磨削弧区任意位置l处的热量ql分别传入砂轮、工件、切屑以及磨削液等周围介质,即

(6)

式中:qwhl、qwl、qchl和qfl分别为进入砂轮、工件、切屑和磨削液等周围介质的热量。

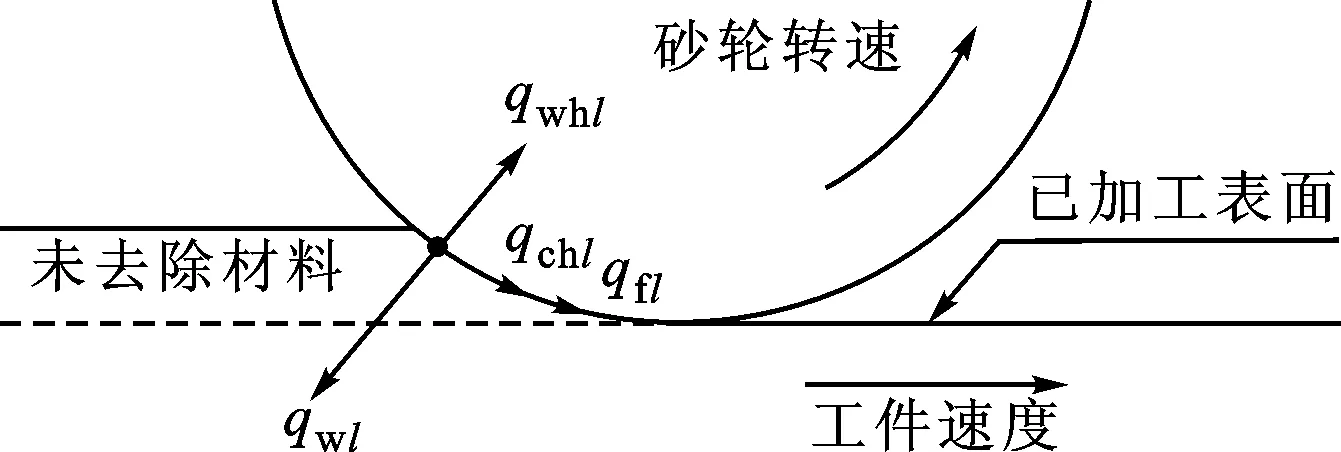
图2 磨削弧区热量分配关系

由于任意时刻磨削弧区产生的切屑很少,本文忽略磨削弧区由切屑带走的热量,即qchl=0。那么,式(6)变为ql=qwhl+qwl+qfl。

传入磨削液等周围介质的热量为

(7)

式中:T0l是温升;T∞是周围环境温度;Tinitial是介质初始温度;hfl是对流换热系数。

基于磨粒接触分析,建立砂轮与工件之间的热量分配比模型[16],表达式为

(8)

式中:k、ρ、c分别是热传导系数、密度、比热容;下标g、w分别表示磨粒、工件;ro是磨粒接触半径。

将式(4)代入式(8),即可得到磨削弧区任意位置l处的砂轮与工件之间的热量分配比

(9)

根据磨粒接触分析[17],可得到以下关系

(10)

那么,磨削弧区进入工件的热源分布qwl可表达为

(11)

1.4 热源分布形状研究

在矩形热源和直角三角形热源分布模型推导时,首先需获得切向磨削力Ft,Ft可通过磨削试验直接测量或利用经验公式求解;再利用公式q=Ftvs/blc计算磨削弧区平均热流密度q;然后分析磨削弧区热量分配关系,求解热量分配比ε,获得进入工件的平均热流密度qw,qw=εq;最后假设进入工件的热源分布形状为矩形或直角三角形,推导矩形热源或直角三角形热源的表达式为

(12)

推导矩形热源或直角三角形热源的表达式时,一般基于两个假设条件。第一,假设磨削弧区总热源分布形状,推导矩形热源的表达式时,假设磨削弧区总热源分布形状为矩形;推导直角三角形热源的表达式时,假设磨削弧区总热源分布形状为直角三角形。第二,假设热量分配比沿磨削弧区均匀分布。

本文通过式(5)获得磨削弧区总热源分布形状,不需假设总热源分布形状。热量分配比沿磨削弧区是变化的[18],本文基于磨粒接触分析,考虑沿磨削弧区变化的磨粒接触半径,得到了沿磨削弧区变化的热量分配比,如图3所示。因此,本文不需要以上两个假设条件即可建立磨削弧区热源分布形状。

在相同的磨削工艺参数下,将利用式(12)得到的矩形热源、直角三角形热源和利用式(11)得到的热源绘于图3。将利用式(11)得到的热源分布数据进行曲线拟合,发现利用下式的四次多项式函数可以得到准确的拟合结果

qwl=1.706×107[0.005-0.199(l/lc)+

1.947(l/lc)2-1.964(l/lc)3+4.533(l/lc)4]

(13)

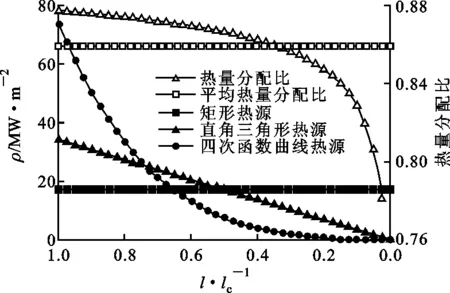
vs=20 m/s; vw=1 500 mm/min; ae=30 μm图3 热源分布及热量分配比分布

由于在不同的磨削工艺参数下,利用式(11)得到的热源分布形状均接近四次多项式函数曲线,只是具体热流密度值不同,因此,将利用式(11)得到的热源命名为四次函数曲线热源。

2 平面磨削瞬态温度场有限元模型

如图2所示,进入工件的热量qwl一部分传入未去除材料,在后续磨削过程中随切屑一起离开磨削弧区。砂轮接触表面对应的圆心角很小,可将磨削弧区近似看作倾斜平面。因此,建立如图4所示的瞬态磨削温度场有限元模型,模拟工件磨削温度场。

2.1 几何模型及网格划分

将工件看作二维平板,为方便加载热源,工件长度取20倍的磨削接触弧长,高度与工件实际高度一致,取12 mm。沿工件高度方向,工件表面附近划分细密网格,以捕捉表层较大的温度梯度,远离工件表面的位置,划分相对稀疏的网格;沿磨削方向,网格长度划分为磨削弧长的1/20。采用单元生死功能,模拟已被去除的工件材料,如图4中虚线所示。

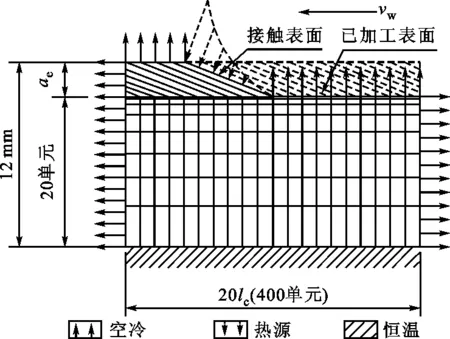
图4 瞬态磨削温度场有限元建模

2.2 材料特性

考虑工件材料性能随温度的变化,相关热物性参数如表1所示。

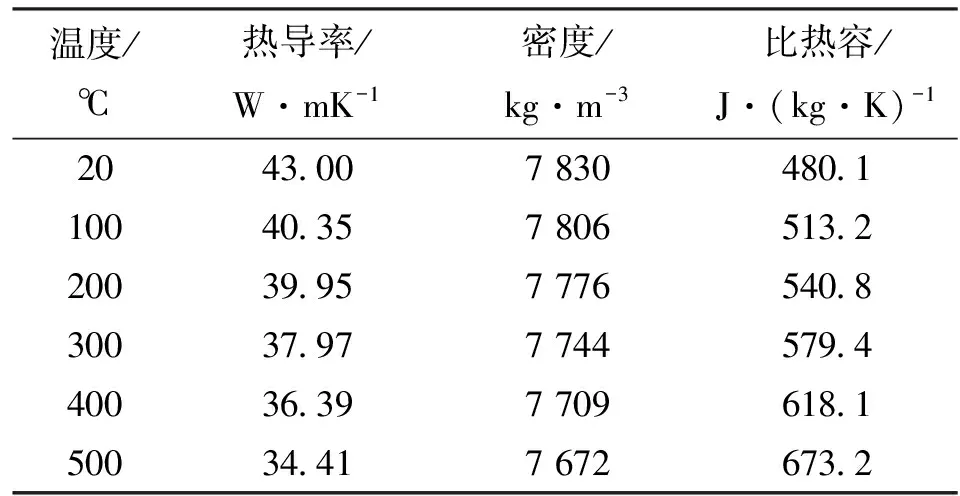
表1 淬硬轴承钢GCr15的热物性参数[19]

2.3 边界条件

工件初始温度设为20 ℃,干磨时,工件与周围环境之间发生对流换热,但是对流换热系数的具体数值难以确定,只能得到对流换热系数的大概范围为20～100 W/(m2·K)。经分析发现,对流换热系数从20 W/(m2·K)增加到100 W/(m2·K),工件最高温度仅降低5 ℃左右,这说明有限元模型对对流换热系数的微小变化并不敏感,因此设置对流换热系数为60 W/(m2·K)。

由于直角三角形热源比矩形热源更加准确,因此,本文在模拟工件磨削温度场时,将直角三角形热源和四次函数曲线热源作为移动热源,加载到有限元模型的接触表面上,沿磨削方向步进,并相应地更新边界条件,模拟瞬态磨削温度场。

3 磨削温度测量试验

平面磨削试验在MKL7120×6 CNC磨床上进行,在每次磨削之前,进行砂轮修整,磨削试验参数如表2所示。平面磨削试验共进行了9组,工艺参数如表3所示。使用YDXM-III97型测力仪测量磨削力,经JY5002型电荷放大器和A/D采集卡后,输入计算机,利用Labview软件采集记录电压信号。

表2 磨削试验参数

表3 磨削试验工艺参数

采用NEC-TH5104R型热成像仪测量磨削温度,最小焦距为30 cm,成像像素为255×223,空间分辨率为0.66 mm左右,测温范围为150～1 500 ℃。测量磨削温度前,使用丙烯酸树脂均匀地将工件表面涂黑,丙烯酸树脂的发射率为0.94。磨削时,固定热成像仪,保证热成像仪与磨削弧区之间无相对运动,磨削温度测量试验示意如图5所示。

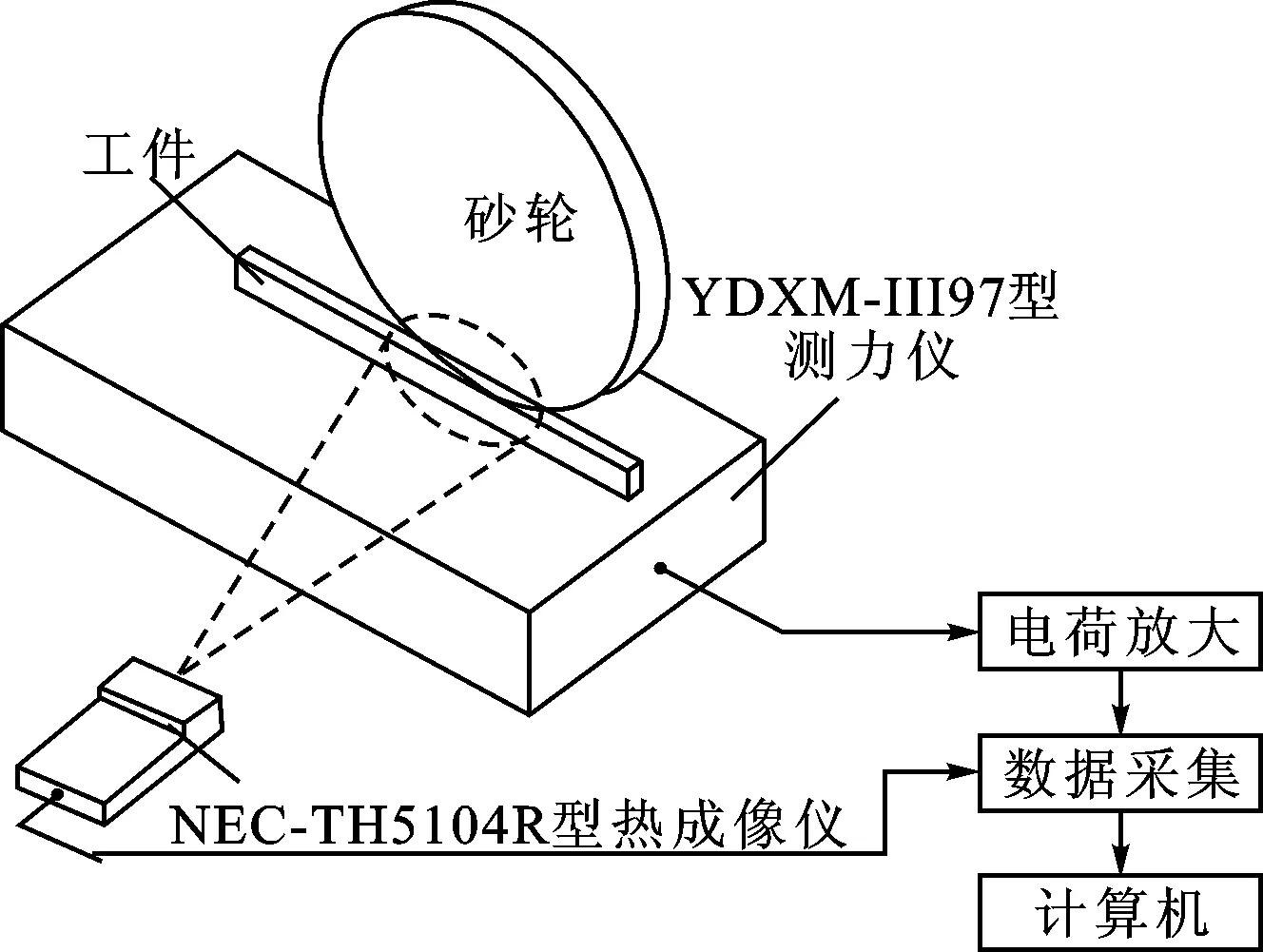
图5 磨削温度测量试验示意图

4 结果及讨论

图6为热成像仪测量云图与有限元模拟云图之间的对比。从图中可以发现,有限元模型可以获得与热成像仪相似的温度场分布云图。两云图略有差异,产生差异的主要原因是:①分辨率不同,热成像仪的分辨率为0.66 mm左右,而有限元模型的分辨率为0.16 mm左右;②温度范围不一致,热成像仪的温度范围是150～1 500 ℃,而有限元模型的温度范围是0～1 500 ℃;③数据处理软件不同,虽然两云图都是通过MATLAB软件绘制,但是热成像仪通过自带软件输出温度数据,而有限元模型通过ANSYS软件输出温度数据。

vs=20 m/s; vw=1 500 mm/min; ae=30 μm图6 热成像仪测量云图与有限元模拟云图的对比

在磨削温度场有限元模型中,分别施加四次函数曲线热源和直角三角形热源,得到的磨削弧区已加工表面温度与试验温度的对比见图7。经分析发现,直角三角形热源产生的最高温度比四次函数曲线热源产生的最高温度稍高,四次函数曲线热源产生的最高温度更加靠近磨削弧区前端,加载四次函数曲线热源获得的温度分布比加载直角三角形热源获得的温度分布更加接近热成像仪测得的温度分布。

vs=20 m/s; vw=1 500 mm/min; ae=30 μm图7 磨削弧区已加工表面温度分布

图8为有限元模型预测的与热成像仪测得的磨削弧区最高温度之间的相对误差。由图8可以发现,有限元模型预测的最高温度最大误差为15.3%,最小误差为2.24%。

图8 磨削弧区最高温度预测误差

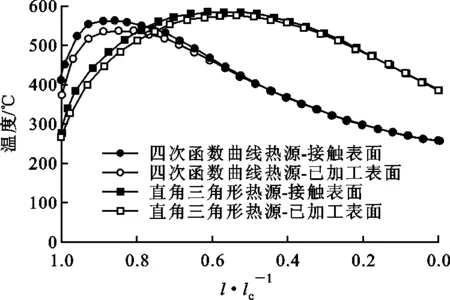
vs=20 m/s; vw=1 500 mm/min; ae=30 μm图9 磨削弧区温度分布

图9为磨削弧区已加工表面温度与接触表面温度之间的比较。由图9可以发现,已加工表面与接触表面的温度分布趋势一致,沿磨削弧区后端到前端,随着接触表面与已加工表面之间距离的增加,两者之间的温度差也逐渐增大。由于存在未去除材料,造成磨削弧区已加工表面温度比接触表面温度低。但是,由于磨削深度较小,已加工表面和接触表面之间的温度相差不大。

5 结 论

本文研究了磨削弧区热源分布形状,分析了工件瞬态磨削温度场,结论如下。

(1)本文建立的磨削弧区热源分布模型和磨削温度场有限元模型可以准确地预测磨削温度,磨削弧区最高温度预测值与实测值之间的误差在2.24%～15.3%之间。

(2)利用本文研究方法,不需预先假设沿磨削弧总热源分布形状及热量分配比一致,即可获得磨削弧区进入工件的热源分布形状。

(3)直角三角形热源并不能准确地描述磨削弧区热源分布形状,磨削弧区热源分布形状更接近四次多项式函数曲线。

[1] MALKIN S, GUO C. Thermal analysis of grinding [J]. CIRP Annals: Manufacturing Technology, 2007, 56(2): 760-782.

[2] 张磊. 单程平面磨削淬硬技术的理论分析和试验研究 [D]. 济南: 山东大学, 2006.

[3] GUO C, WU Y, VARGHESE V, et al. Temperatures and energy partition for grinding with vitrified CBN wheels [J]. CIRP Annals: Manufacturing Technology, 1999, 48(1): 247-250.

[4] ROWE W B, BLACK S C E, MILLS B, et al. Experimental investigation of heat transfer in grinding [J]. CIRP Annals: Manufacturing Technology, 1995, 44(1): 329-332.

[5] ZHANG L, MAHDI M. Applied mechanics in grinding: IV The mechanism of grinding induced phase transformation [J]. International Journal of Machine Tools and Manufacture, 1995, 35(10): 1397-1409.

[6] LI B, ZHU D, PANG J, et al. Quadratic curve heat flux distribution model in the grinding zone [J]. The International Journal of Advanced Manufacturing Technology, 2011, 54(9/10/11/12): 931-940.

[7] 毛聪. 平面磨削温度场及热损伤的研究 [D]. 长沙: 湖南大学, 2008.

[8] SHAH S M, NELIAS D, ZAIN-UL-ABDEIN M, et al. Numerical simulation of grinding induced phase transformation and residual stresses in AISI-52100 steel [J]. Finite Elements in Analysis and Design, 2012, 61: 1-11.

[9] GUO C, MALKIN S. Inverse heat transfer analysis of grinding: part 1 Methods [J]. Journal of Manufacturing Science and Engineering, 1996, 118(1): 137-142.

[10]GUO C, MALKIN S. Inverse heat transfer analysis of grinding: part 2 Applications [J]. Journal of Manufacturing Science and Engineering, 1996, 118(1): 143-149.

[11]HONG K K, LO C Y. An inverse analysis for the heat conduction during a grinding process [J]. Journal of Materials Processing Technology, 2000, 105(1): 87-94.

[12]KIM H J, KIM N K, KWAK J S. Heat flux distribution model by sequential algorithm of inverse heat transfer for determining workpiece temperature in creep feed grinding [J]. International Journal of Machine Tools and Manufacture, 2006, 46(15): 2086-2093.

[13]BROSSE A, NAISSON P, HAMDI H, et al. Temperature measurement and heat flux characterization in grinding using thermography [J]. Journal of Materials Processing Technology, 2008, 201(1): 590-595.

[14]ROWE W B, MORGAN M N, QI H S, et al. The effect of deformation on the contact area in grinding [J]. CIRP Annals: Manufacturing Technology, 1993, 42(1): 409-412.

[15]WANG D, GE P, BI W, et al. Grain trajectory and grain workpiece contact analyses for modeling of grinding force and energy partition [J]. The International Journal of Advanced Manufacturing Technology, 2014, 70(9/10/11/12): 2111-2123.

[16]ROWE W B. Thermal analysis of high efficiency deep grinding [J]. International Journal of Machine Tools and Manufacture, 2001, 41(1): 1-19.

[17]HADAD M, SADEGHI B. Thermal analysis of minimum quantity lubrication-MQL grinding process [J]. International Journal of Machine Tools and Manufacture, 2012, 63: 1-15.

[18]JU Y, FARRIS T N, CHANDRASEKAR S. Theoretical analysis of heat partition and temperatures in grinding [J]. Journal of Tribology, 1998, 120(4): 789-794.

[19]SHAH S M A. Prediction of residual stresses due to grinding with phase transformation [D]. Lyon, France: INSA de Lyon, 2011.

(编辑 杜秀杰)

Heat Source Profile in Grinding Zone

WANG Dexiang1,GE Peiqi1,2,BI Wenbo1,ZHENG Chuandong1

(1. School of Mechanical Engineering, Shandong University, Jinan 250061, China; 2. Key Laboratory of High-Efficiency and Clean Mechanical Manufacture at Shandong University, Ministry of Education, Jinan 250061, China)

A heat source distribution model in grinding zone is established with probability statistical method to reveal the residual stress field induced by the coupling of grinding force and grinding heat following grain trajectory analysis and grain contact analysis. Heat partition analysis in grinding zone is performed in the modeling of heat source distribution. Heat source profile was always assumed to be rectangular or triangular in the previous studies, however rectangular or triangular heat source can not describe the heat source profile accurately. On the assumption of uniform heat partition ratio in grinding zone and without providing profile of total heat source in advance, the heat source distribution model enables to obtain the heat source profile in grinding zone. Finite element method is used to simulate grinding temperature field. An infrared thermal imager is used to measure grinding temperature field. A comparison indicates that the simulations coincide well with the measurements of grinding temperature field, and the errors of the maximum temperature in grinding zone range from 2.24% to 15.3%. The heat source distribution in grinding zone approaches the profile of quartic polynomial curve.

heat source distribution; heat source profile; heat partition ratio; grinding temperature field

2015-01-28。 作者简介:王德祥(1988—),男,博士生;葛培琪(通信作者),男,教授,博士生导师。 基金项目:国家“973计划”资助项目(2011CB706600)。

时间:2015-05-04

10.7652/xjtuxb201508019

TG580.1

A

253-987X(2015)08-0116-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150504.0900.005.html