考虑热-变形耦合的主轴-轴承系统瞬态热特性分析

米维,闫柯,吴文武,洪军,刘光辉

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)



考虑热-变形耦合的主轴-轴承系统瞬态热特性分析

米维,闫柯,吴文武,洪军,刘光辉

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)

为了更准确地预测主轴-轴承系统的温度场并实时监测关键零部件的温升情况,建立了考虑热-变形耦合的轴系瞬态热网络模型。根据热弹性力学理论,推导出主轴-轴承系统在装配应力、离心应力和热应力综合作用下的径向复合变形方程,基于热网络法优选试验轴系关键部件作为温度节点,综合考虑润滑剂黏温效应及轴系径向复合应力与变形,实时修正轴系热源、热边界条件等特性参数,实现了温度场与变形的耦合分析。通过编程求解获得了不同条件下轴承的瞬态温升曲线及轴系关键热参数的瞬态特性,结果表明,主轴转速越高,轴系热平衡温度越高,平衡时间越短;迭代步长的选取只影响温升曲线的收敛时间,不影响稳态温度值。与试验数据的对比结果表明,使用该瞬态热网络模型预测轴系温度场可显著降低计算误差。

主轴-轴承系统;热-变形耦合;瞬态热特性;热网络法

主轴-轴承系统的温度场分布及关键零部件的温升过程是其优化设计的重要指标,瞬态热分析对于准确预测轴系温度场及瞬态热特性、提高轴系性能具有重要意义。运转中的轴系属于热时变系统,其润滑剂黏度、热源、热边界条件等热特性参数随其瞬态温度场时刻变化。同时,在初始装配应力、离心应力和热应力的共同作用下,轴系高速运转时的复合变形会导致轴承结构参数改变,引起热源、热阻等热参数的变化。因此,进行主轴-轴承系统瞬态热特性分析,需要综合考虑热与变形耦合效应下轴系温度场与变形的瞬态特性。

基于有限元法的轴系热分析已经较为成熟[1-2]。文献[1]利用有限元方法对机械主轴稳态温度场和结构变形进行了计算,并通过温升实验进行了验证。文献[3]建立了高速电主轴的有限差分热模型,并基于此模型进行了稳态和瞬态温度场分析。由于有限元法在网格划分、边界条件处理等方面的限制,其计算过程一般相对繁琐,相比之下,热网络法在处理复杂系统传热问题时更具优势[4]。文献[5]利用热网络法求解了某主轴系统的稳态温度分布,并分析了预紧力、转速等参数对节点温度的影响。但是,目前热网络法普遍应用于轴系稳态温度场求解,而且计算时忽略了轴承热源及热边界条件等参数的动态变化,造成温度场计算结果误差较大,且无法预测关键零部件的瞬态温升过程及轴系的热平衡时间。另外,轴系在运转中由复合应力引起的变形会导致其热参数的变化,从而影响轴系的温度场分布。文献[6-7]等分别研究了装配应力、离心应力及热应力与轴系变形的关系,但没有考虑瞬态温度场下3种应力与变形的耦合效应。综上,该领域缺乏一种不依赖于有限元方法且考虑热-变形耦合的瞬态热分析模型。

本文首先推导出主轴-轴承系统在初始装配应力、离心应力和热应力共同作用下的径向应力-变形方程,在此基础上,基于热网络法确定轴系主要热特性参数,建立瞬态热平衡方程,在迭代过程中将轴系温度场与变形耦合,构建瞬态热网络模型。通过求解,获得了轴系温度场及热参数的瞬态变化特性,分析了转速及迭代步长对轴承瞬态温升曲线的影响,并结合试验验证了瞬态模型的准确性。

1 主轴-轴承系统径向变形

主轴及轴承的装配关系如图1所示,主轴转子内半径为a,轴承内圈的内、外半径分别为b、c,外圈的内外半径分别为d、e,其对应的稳态温度值依次为T1、T2、T3、T4、T5。

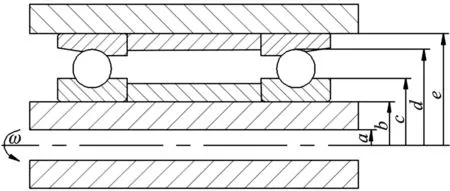
图1 主轴-轴承系统装配关图

1.1 轴承内、外圈径向变形

轴承内、外圈的截面尺寸远大于其轴向厚度,可以将其看作一个温度场轴对称的空心圆盘等效为热弹性体的平面应力问题进行求解[6]。

以轴承内圈为研究对象,根据热弹性力学理论,联立平面应力问题的平衡方程、几何方程及应力-应变方程,可以得到如下关系

(1)

式中:ν为材料泊松比;E为材料弹性模量;α为材料热膨胀系数;ρ为材料密度;ω为旋转角速度;r为转子半径;u为径向变形。

根据传热学理论,对于内、外半径分别为ri和ro,内、外表面温度分别为Ti和To的单层圆筒,其温度沿半径方向的分布满足对数曲线[8]

(2)

由式(2)可知,温差ΔT沿半径方向也满足相应的对数曲线。将温差关系代入式(1)中,求得轴承内圈径向变形及径向应力的表达式如下

(3)

(4)

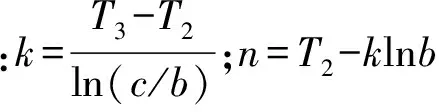
若轴承内圈与主轴间的过盈量为δ1,则其装配应力p1可通过下式求得[9]

(5)

轴承内圈内径与主轴的配合应力为p1,内圈外径为自由面,因此轴承内圈受力的边界条件可描述为

(6)

将式(6)代入式(4),求得常数C1、C2,再将C1、C2的值代入式(3),则可得到轴承内圈在半径r处的径向变形值。

轴承外圈的变形计算与内圈类似,区别在于外圈在轴系运转过程中静止不动,因此不需要考虑离心应力的影响,即令式(3)、式(4)中ω=0,再结合轴承外圈应力边界条件

(7)

可得轴承外圈径向变形值,p2为轴承外圈与轴承座间的配合应力,若轴承外圈与轴承座为间隙配合,可视为负过盈代入式(5)计算装配压力。

1.2 主轴轴颈径向变形

主轴转子轴向尺寸较大,截面尺寸相对较小,可以等效为一个等截面梁,按轴对称平面应变问题求解[6]。

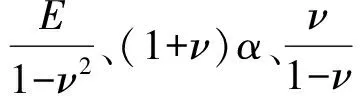
(8)

可求得主轴轴颈在半径r处的径向变形值。

2 轴系瞬态热网络模型的建立

2.1 热节点布置及热网络参数确定

试验主轴的结构简图及热网络节点布置如图2所示。整个系统关于主轴中心线对称,不需要考虑圆周方向的传热,根据试验台轴系结构布局及材料分布,将系统划分为46个热网络节点,图中“·”代表热节点位置。采用整体法[10]计算轴承发热,并认为轴承滚动体承担一半的发热量,内外圈各承担1/4的发热量[11]。

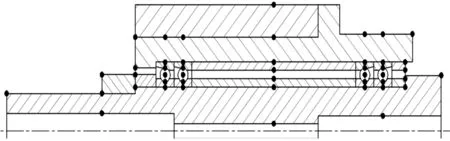
图2 试验主轴结构简图及热节点分布

在一维稳态传热过程中,导热热阻和对流热阻的计算模型分别为[4]

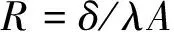
(9)

R′=1/hA

(10)

式中:λ为材料热导率;δ为导热特征长度;A为换热面积;h为对流换热系数。

将空心轴、轴承内外圈等部件均简化为空心圆筒,根据热阻定义及材料和尺寸参数,可求得各节点间的轴向及径向热阻。

由传热学理论可知,对流换热系数为

h=Nuλa/de

(11)

式中:λa为空气热导率;de为对流换热特征长度,对于圆柱取外表面直径;Nu为努赛尔数,根据对流换热方式的不同由相应经验公式[12]求得。

2.2 瞬态热平衡方程建立

利用热网络法建立的稳态热平衡方程的一般形式为[5]

(12)

式中:To为待求节点温度值;Ti为周围与之相关各节点的温度值;Ro-i为节点间热阻(i=1,2,3,4);Qo为该节点发热量。

将式(11)推广到整个传热系统中,即得到系统的稳态热平衡方程组,用矩阵形式表达为

GT=Q

(13)

式中:G为热导矩阵,是由节点间热阻值组成的n阶方阵,n为节点个数;T为待求解的温度场矩阵,Q为热源矩阵,T和Q均为n维列向量。对于无内置电机的主轴-轴承系统,热源节点Q(即轴承节点)取用整体法计算出的轴承发热量,其余节点Q取0。

主轴-轴承系统从开始运转至稳态前满足热流平衡原理,即任意时刻节点的净热流量等于该节点相关体积内能的增加[13]

qi=CiρiVidTi/dτ

(14)

式中:qi、ρi、Ci、Vi、Ti分别代表节点i处的净热流量、材料密度、材料比热容、材料体积和温度;τ为时间;dTi/dτ为节点i处的温升率。

结合稳态热平衡方程,根据能量守恒原则建立瞬态的热流平衡方程

(15)

为了得到轴系瞬态温度场的数值解,将连续时间τ按一定的步长Δτ离散为一系列小的时间序列

(16)

则τk+1时刻的温度场可由τk时刻的温度场递推得到

(17)

联立式(15)、式(17),可得节点瞬态热平衡方程数值解形式如下

(18)

瞬态热过程的每一步都可以看作近似稳态热过程,因此在迭代过程中只需求解相应的线性方程组,再将所得温度场作为输入条件即可递推得到下一时刻的温度场结果。

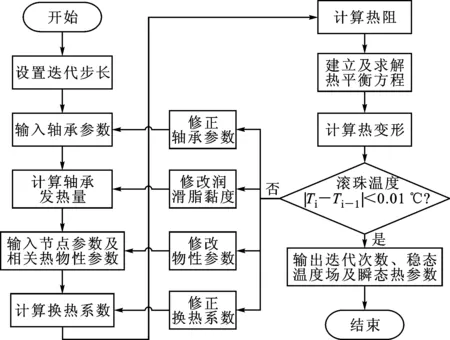
图3 考虑热-变形耦合的瞬态温度场求解流程

综合上述分析,可以得到用热网络法求解轴系瞬态温度场的一般流程(如图3所示)。给定主轴转速等初始条件并确定所需计算精度,所有节点初始温度均取环境温度,计算出相应的热特性参数,建立并求解瞬态热平衡方程。根据每一步求解的节点温度修正润滑脂黏度及换热系数,同时利用主轴及轴承关键节点温度求出其径向变形,修正发热量及相关热阻阻值,当温度场计算结果满足给定收敛条件时停止迭代。此时可以得到满足给定精度的最小迭代次数,再按迭代过程将节点温度、变形等中间变量依次输出,即可得到所需热参数的瞬态特性曲线。

3 计算结果及试验分析

3.1 轴承瞬态温升曲线

选取轴承型号为NSK7014C,设环境温度为21 ℃,迭代步长Δτ=0.1,根据上述瞬态热网络模型绘制试验轴系在不同转速下轴承外圈的瞬态温升曲线,如图4所示。图5为轴系在6 000 r/min时不同迭代步长下轴承外圈的温升曲线。从这两图可以看出:轴承温度随时间推移逐渐升高,在轴系达到热平衡后趋于稳定;轴承的平衡温度随转速上升而升高;转速越高迭代步长越大,热平衡时间越短,曲线收敛越快;迭代步长只影响收敛速度,不影响最终的稳态温度值。

图4 不同转速下轴承瞬态温升曲线

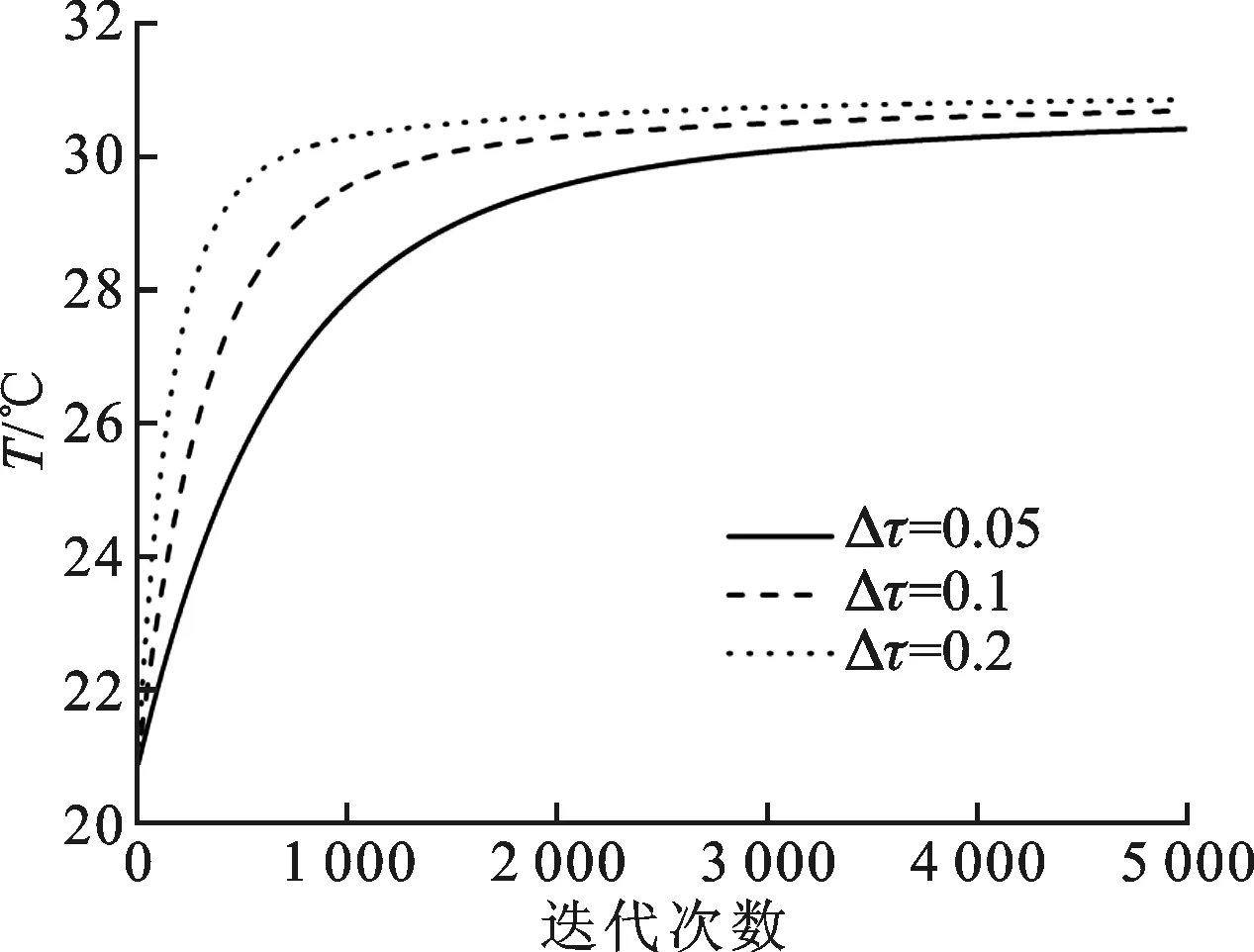
图5 迭代步长对瞬态热特性的影响

3.2 热参数的瞬态特性

输出迭代过程的中间变量,可以得到轴承发热量、热阻等参数的瞬态特性。取图4中相同的环境温度及迭代步长,设定主轴转速为6 000 r/min,输出每一步的轴承发热量并绘制其瞬态特性曲线,如图6所示。由图可知,在轴系运转过程中,轴承发热量逐渐降低直至趋于稳定,这是由于轴承润滑剂存在黏温效应,其黏度随温度升高而降低,因此轴承发热量随温升逐渐减小。

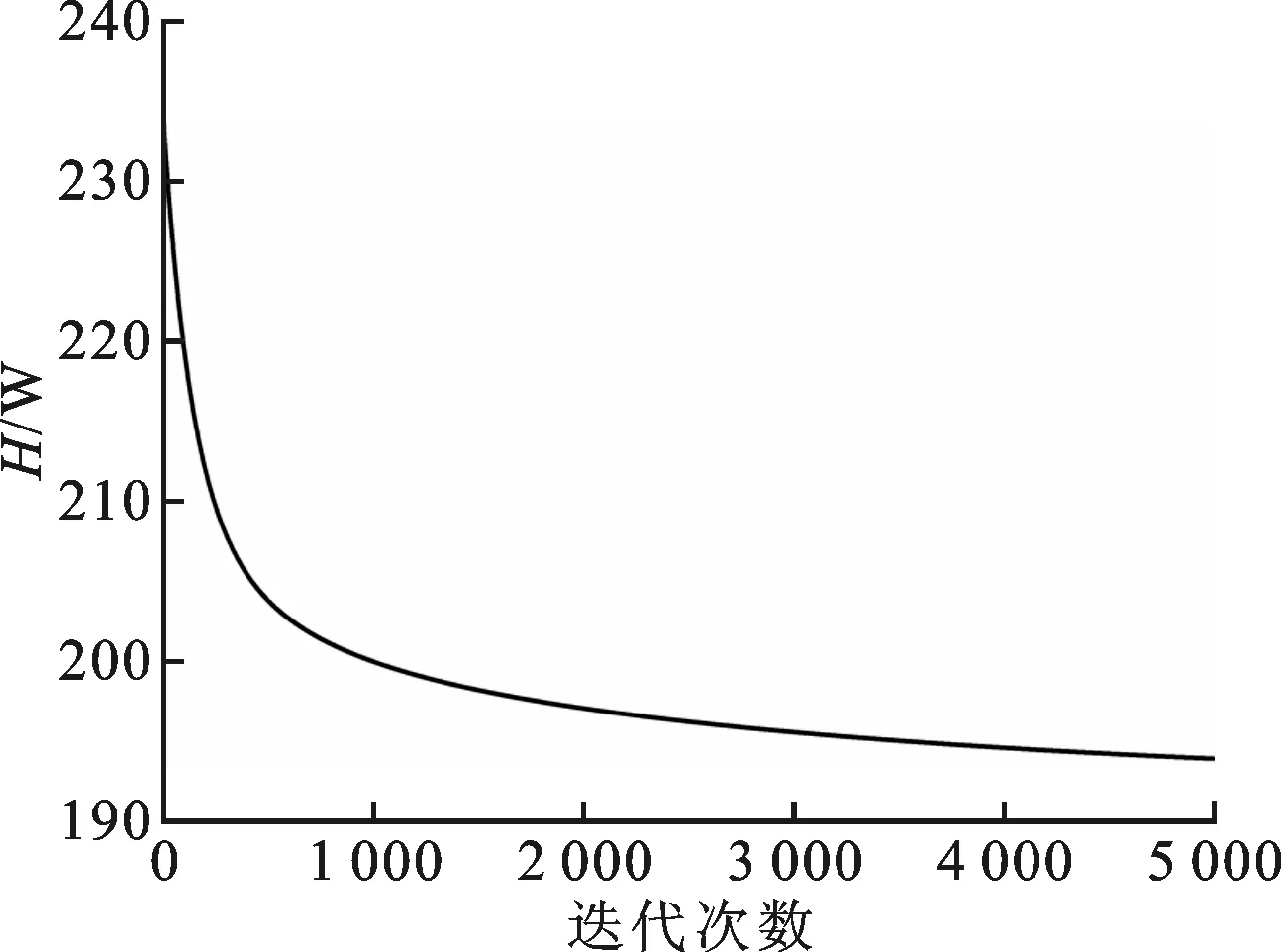
图6 轴承发热量瞬态特性

受初始装配应力、离心应力和热应力的综合作用,在轴系运转过程中,主轴及轴承的几何尺寸发生改变,导致热节点间热阻的改变。图7为相同初始条件下轴承内圈外径随时间变化的曲线。由图可知,随着时间推移,内圈外径受应力作用逐渐增大,当轴系达到热平衡时趋于稳定。

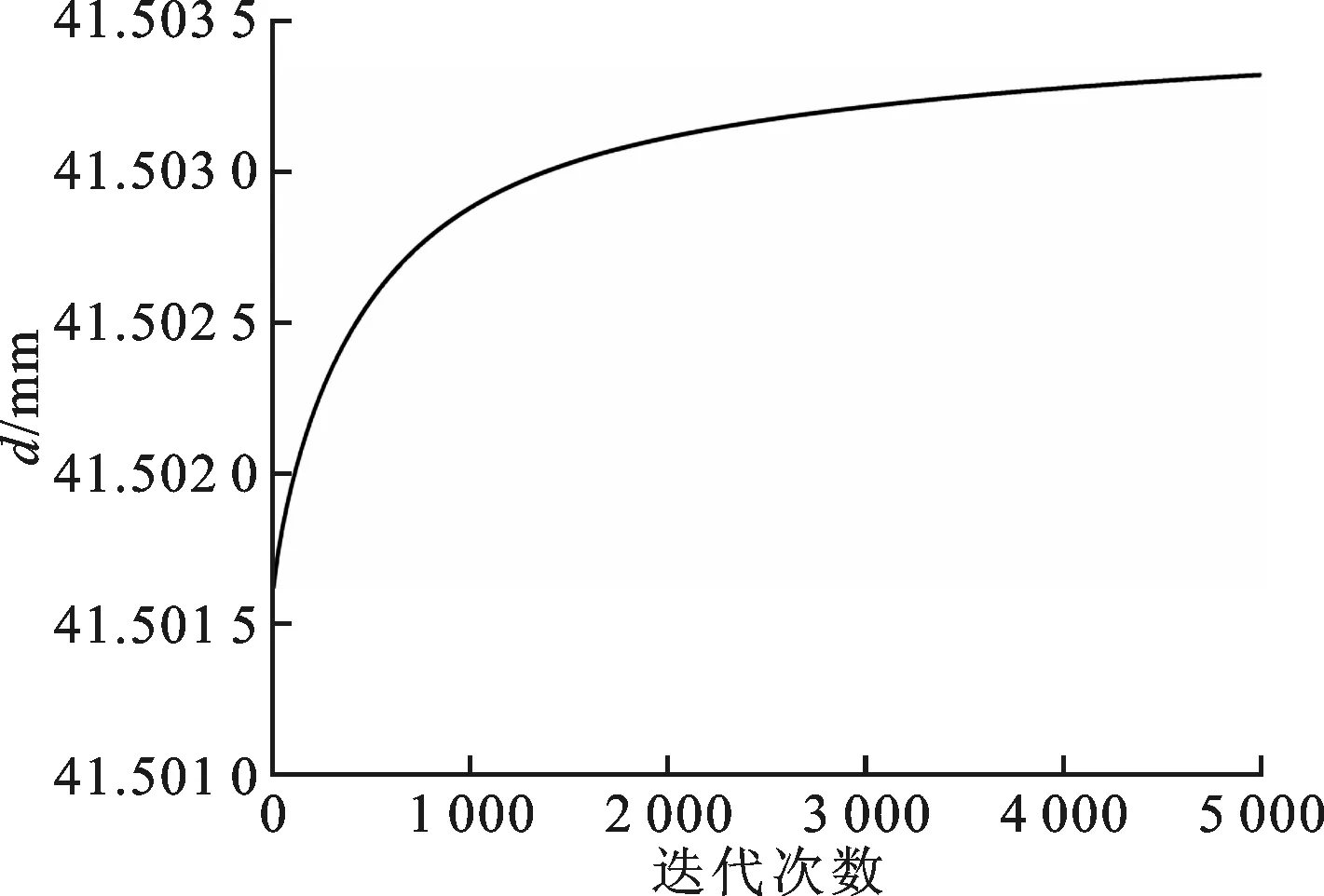
图7 内圈外径瞬态变化特性

由图6可以看出,轴系在热平衡过程中除温度场外,热参数也在瞬态变化,传统的稳态热网络模型忽略了热参数的动态性,将其简化为固定值,因此会对结果造成较大误差。

3.3 试验验证

试验台及传感器布置如图8所示,试验台轴系及轴承的基本信息及试验工况如表1所示。

图8 试验主轴及传感器布置

主轴类型机械主轴驱动方式皮带驱动润滑方式脂润滑轴承型号NSK7014CTYNSULP4轴承安装方式DBB传感器MISUMI温度传感器采集系统NI数采系统环境温度/℃235测量转速/r·min-12000，4000，6000，8000

取与试验工况相同的环境温度及转速等工况,迭代步长Δτ=0.1,根据瞬态热分析流程编制MATLAB程序并求解,获得试验台轴承的瞬态温升曲线,与试验测量结果对比如图9所示。从图中可以看出,本文提出的瞬态模型求解结果在一定转速范围内与试验数据吻合较好。

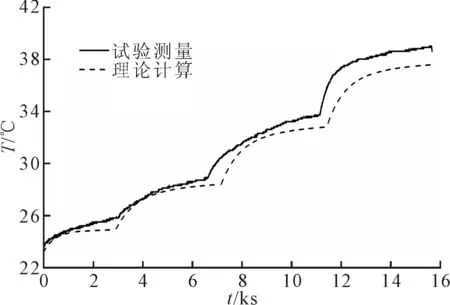
图9 前轴承外圈瞬态温升曲线与试验结果对比

结合试验数据对比了稳态热模型与瞬态热模型,并将两种模型得出的各转速下轴承外圈平衡温度与试验测量结果进行对比,结果如图10所示。由图10可知,稳态模型计算出的温度场与试验偏差较大,最大误差达到26.2%,而瞬态模型的最大误差仅为7.7%。这是由于稳态模型忽略了轴系热参数的动态变化,而瞬态热网络模型考虑因素更为全面,更真实地模拟了实际传热过程,因此计算结果与试验测量结果更为接近。

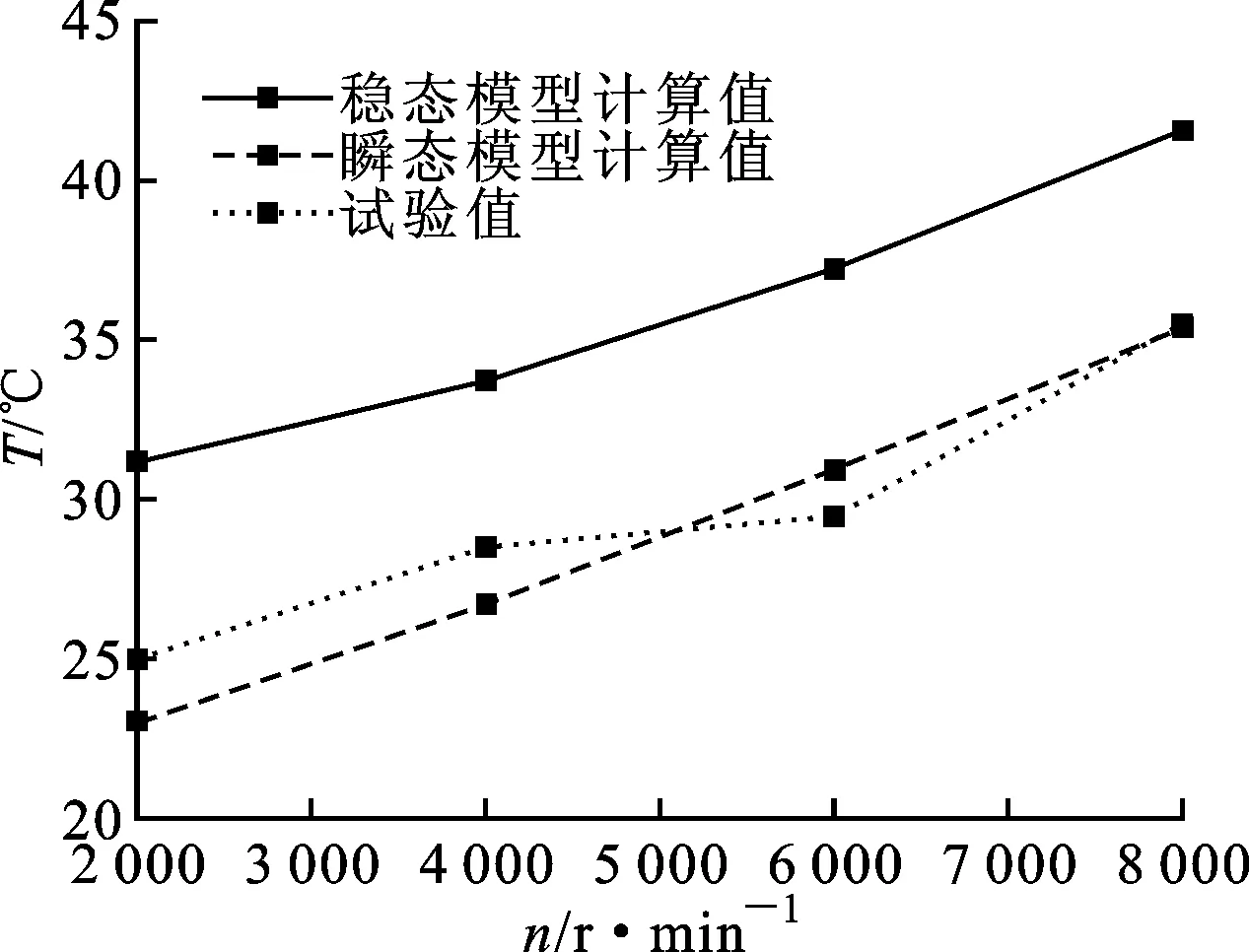
图10 轴承稳态温度随转速变化对比

4 结 论

(1)本文在推导主轴-轴承系统在装配应力、离心力和热应力共同作用下的径向应力-变形方程的基础上,结合黏温效应及径向变形实时修正热特性参数,建立了考虑热-变形耦合的主轴-轴承系统瞬态热网络模型。

(2)不同条件下的轴承瞬态温升曲线表明,由瞬态热网络模型求解的轴系热平衡时间随转速及迭代步长的增加而减小,而稳态平衡温度只与主轴转速有关。

(3)轴系热特性参数随温度场时刻变化,轴承发热量由于黏温效应逐渐减小,轴承径向尺寸受复合应力作用逐渐增大。

(4)结合试验验证了瞬态热网络模型的准确性并对比了稳态与瞬态模型,结果表明,在中、低转速下,使用本文提出的瞬态热网络模型预测轴系温度场可明显降低误差。但是,由于本文所用试验主轴设计转速较低,无法验证模型在较高转速下的精度。另外,该模型未考虑润滑剂的动压作用、零部件的加工精度及材料的本构性能等影响因素,因此仍存在一定局限性。

[1] HOLKUP T, CAO H, KOLAR P. Thermo-mechanical model of spindles [J]. CIRP Annals: Manufacturing Technology, 2010, 59: 365-368.

[2] 陈小安, 刘俊峰, 合烨, 等. 高速电主轴热态性能及其影响 [J]. 机械工程学报, 2013, 49(11): 135-142. CHEN Xiao’an, LIU Junfeng, HE Ye, et al. Thermal properties of high speed motorized spindle and their effects [J]. Journal of Mechanical Engineering, 2013, 49(11): 135-142.

[3] BOSSMANNS B, TU J F. A thermal model for high speed motorized spindles [J]. International Journal of Machine Tools & Manufacture, 1999, 39: 1345-1366.

[4] 刘昌华, 骆广进, 何卫, 等. 基于热网络的某主轴系统稳态热分析 [J]. 中国机械工程, 2010, 21(6): 631-635. LIU Changhua, LUO Guangjin, HE Wei, et al. Steady state thermal analysis of a spindle system based on thermal network [J]. China Mechanical Engineering, 2010, 21(6): 631-635.

[5] 黄东洋, 洪军. 热阻网络法在轴系温度场求解中的应用 [J]. 西安交通大学学报, 2012, 46(5): 63-66. HUANG Dongyang, HONG Jun. Thermal resistance network for solving temperature field in spindle system [J]. Journal of Xi’an Jiaotong University, 2012, 46(5): 63-66.

[6] 曹宏瑞, 李兵, 陈雪峰, 等. 高速主轴离心膨胀及对轴承动态特性的影响 [J]. 机械工程学报, 2012, 48(19): 59-64. CAO Hongrui, LI Bing, CHEN Xuefeng, et al. Centrifugal expansion of high-speed spindle and its influences on bearing dynamic characteristics [J]. Journal of Mechanical Engineering, 2012, 48(19): 59-64.

[7] 王保民, 梅雪松. 计入套圈径向热位移的角接触球轴承动力特性分析 [J]. 设计与研究, 2010(4): 61-66. WANG Baomin, MEI Xuesong. Dynamic characteristics analysis of angular contact ball bearing considering radial thermal displacement of ring raceways [J]. Design and Research, 2010(4): 61-66.

[8] 杨世铭, 陶文铨. 传热学 [M]. 4版. 北京: 高等教育出版社, 2006: 16.

[9] 李维特, 黄保海, 毕仲波. 热应力理论分析及应用 [M]. 北京: 中国电力出版社, 2004: 66-67.

[10]HARRIS T A, KOTZALAS M N. 滚动轴承分析: 第一卷 [M]. 万长森, 译. 北京: 机械工业出版社, 2010: 184-186.

[11]BURTON R A, STAPH H E. Thermally activated seizure of angular contact bearings [J]. ASLE Transactions, 1967, 10(4): 408-417.

[12]沈浩, 赵跃超, 聂海强. HMC380卧式加工中心电主轴热态性能分析 [J]. 机械设计与制造, 2011(6): 7-9. SHEN Hao, ZHAO Yuechao, NIE Haiqiang, et al. Thermal characteristics analysis for spindle of HMC80 horizontal machining center [J]. Machinery Design & Manufacture, 2011(6): 7-9.

[13]张永红, 苏华, 刘志全, 等. 行星齿轮传动系统的瞬态热分析 [J]. 航空学报, 2000, 21(6): 542-544. ZHANG Yonghong, SU Hua, LIU Zhiquan, et al. Transient thermal analysis of planetary transmission system [J]. Acta Aeronautica et Astronautica Sinica, 2000, 21(6): 542-544.

(编辑 杜秀杰)

Transient Thermal Property Analysis for Spindle-Bearing System Considering Thermo-Deformation Coupling

MI Wei,YAN Ke,WU Wenwu,HONG Jun,LIU Guanghui

(State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

To predict the temperature field of spindle-bearing system more accurately and monitor the temperature rise of key parts, a transient thermal network model with the coupling of the temperature field and deformation was established. The radial compound stress-deformation equation under the initial assembly stress, centrifugal stress and thermal stress was derived following thermo-elasticity theory. The key system components were picked out as the heat nodes according to thermal network optimization. Taking both temperature-viscosity effect and radial compound stress-deformation into account, several key thermal parameters, such as heat source and thermal boundary conditions, were modified in real time. The coupled temperature field and deformation of spindle-bearing system were analyzed. The transient temperature curves of bearings under different conditions and the transient properties of key thermal parameters were obtained numerically. The results shows that the higher of the spindle speed, the higher of the equilibrium temperature, and the shorter of the equilibrium time. The iterative step can only affect the equilibrium time but not the equilibrium temperature. A comparison with a set of experiments indicates that the transient thermal network model enables to reduce errors remarkably in predicting the temperature field of spindle-bearing system.

spindle-bearing system; thermo-deformation coupling; transient thermal properties; thermal network method

2015-01-28。 作者简介:米维(1991—),女,硕士生;闫柯(通信作者),男,讲师。 基金项目:国家重大科技专项资助项目(2015ZX04014021)。

时间:2015-05-04

10.7652/xjtuxb201508009

TH133.2

A

0253-987X(2015)08-0052-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150504.0900.003.html