用于机械系统固有频率及阻尼比计算的改进频域方法

孟庆虎,,朱永生,刁瑞朋

(西安交通大学机械工程学院,710049,西安)



用于机械系统固有频率及阻尼比计算的改进频域方法

(西安交通大学机械工程学院,710049,西安)

针对传统的机械系统固有频率及阻尼比计算方法中,时域方法易造成主观误差,频域方法存在一定精度限制的问题,提出了一种利用指数衰减正弦信号频谱校正算法计算系统阻尼比和固有频率的新方法。该方法首先利用基于汉宁窗的插值频谱校正方法获得频率偏移量和衰减因子,再结合有阻尼自由振动响应与指数衰减正弦信号的相似性关系求取固有频率,进而获得系统阻尼比和有阻尼固有频率,最终计算出无阻尼固有频率。分别使用传统时域方法和本文提出的频域方法对压电悬臂梁的固有频率及阻尼比进行计算,结果表明新方法拥有更高的计算精度和更好的信噪比适应性。与传统的频率拟合方法相比,本文所提方法也更简单,计算效率更高。

衰减信号;频谱校正;固有频率;阻尼比;压电悬臂梁

系统自由振动幅值逐步减少的过程称为阻尼现象[1],其本质是振动系统能量的转换,即从机械能转换为热能或其他形式能量的过程。阻尼比是指阻尼系数与临界阻尼系数之比,用来表达结构阻尼的大小,描述结构在振动过程中能量的耗散情况。较为精确地获得系统的固有频率和阻尼比,在结构动力学计算、结构故障诊断、振动实时监控、响应预测、荷载识别、能量转换等课题研究和工程实际应用方面,有着很重要的作用。

目前常见的计算系统固有频率和阻尼比的方法可分为时域法和频域法两种。时域法有对数衰减率法、易卜拉欣时域法(Ibrahim time domain, ITD)[2]、少时时域法(spare time domain, STD)[3]、随机减量法[4]等;频域法有半功率带宽法[5]、峰值法、导纳圆法等[6]。其中,时域方法具有操作简单、易于实现等特点,但是该方法需要人工进行选点,会带来一定的主观输入误差。此外,在信噪比较低的信号时域波形上也难以准确地估计信号周期,这也为正确地选点造成了困难。半功率点法应用较广,但存在栅栏效应、能量泄漏的离散谱线上很难精确找到半功率点。传统的频域识别方法在进行快速傅里叶变换(fast Fourier transform, FFT)的时候,亦会导致一定的能量泄漏,从而在精度上受到一定的限制。如何提高阻尼比识别精度,使之便于工程实际应用,便成为了一项难题。

受到指数衰减信号频域插值校正理论的启发,本文提出了一种新型的识别系统固有频率和阻尼比的指数衰减正弦信号频谱校正方法。利用离散傅里叶变换后两相邻谱线的比值关系可以精确获得衰减因子,而这个重要的频谱校正参数与阻尼比存在确定的关系。与传统的时域方法和频域方法相比,本文方法利用校正的信号参数进行计算避免了人工选点造成的主观误差,而通过插值方法校正出的固有频率和阻尼比基本不受采样率的影响,具有较高的估计精度。同时,本文方法又具有较强的适应性和更简单的计算过程,并适用于多模态的阻尼比的计算。使用本文方法计算了压电悬臂梁固有频率和阻尼比,并与传统时域方法进行了对比,获得了较为准确的结果,证明本文所提方法可以作为计算系统固有频率和阻尼比的一种可选方法。

1 方法描述

1.1 基于频域差值的非平稳信号参数识别方法

由M个频率分量组成的指数衰减正弦信号一般形式为

(1)

式中:Am、fm、φm为第m个频率分量的幅值、频率、初相位;αm为第m个频率分量的衰减因子,该参数表征指数衰减正弦信号的衰减速率,衰减因子越大,信号幅值的衰减速率越快;N为采样点数。其中一单频指数衰减正弦信号可表示为

(2)

式(2)的离散傅里叶变换为

X[k]=A0ejφ0W[k-f0;α0],k=0,…,N-1

(3)

式中:W[k-fm;αm]由下式给出

(4)

假设频率f0的理论位置为θ0,其两侧的两根离散谱线的位置分别为k0-1和k0,则存在如下关系

(5)

由式(3)可知,f0两侧的两根谱线对应值为

(6)

由式(5)和式(6)可知,f0两侧两根谱线的离散傅里叶变换比值为

(7)

定义变量

(8)

将式(4)和式(8)代入式(7),可解出τ的值为

(9)

由式(8)可知,τ为一复数,根据复数模和幅角的定义可知

(10)

式中:arg(τ)为τ的幅角。

因此,指数衰减正弦信号频率的校正值为

(11)

由式(3)可知

A0=|X[k]|/|W[-δ0;α0]|

φ0=arg(X[k])-arg(W[-δ0;α0])+π/2

(12)

基于矩形窗的频域差值方法存在频谱泄漏大、衰减因子偏差较大的不足。为了有效地抑制频谱泄漏的影响,提高频谱参数估计的精度,刁瑞朋等提出了基于汉宁窗的指数衰减正弦信号矢量插值频谱校正方法并推导出了具体的实现公式,可获得衰减因子和频率偏移量的校正值[7]

(13)

(14)

频率的校正值为

(15)

幅值和相位的校正值为

(16)

(17)

至此,我们获得了指数衰减正弦信号基于汉宁窗的插值频谱校正公式。为了方便起见,将此插值频谱校正方法简称为HDIDFT(Hanning damping interpolated discrete Fourier transform)。

本文拟采用基于汉宁窗的指数衰减正弦信号矢量插值频谱校正方法,并根据振动力学的公式,提出一种计算系统阻尼比和固有频率的方法。

1.2 基于频域方法的系统固有频率和阻尼比计算

由振动力学知识可知,系统欠阻尼情形单自由度系统的自由振动响应[8]为

(18)

根据三角函数和差化积公式,式(18)可表示为

(19)

其中

式(19)表明,欠阻尼情形的单自由度系统对初始条件的响应是一种振幅按指数规律逐渐衰减的简谐振动,与指数衰减信号式(1)具有相同的表示形式。对比两个公式可以看出,式(19)中的-ζωn即是式(1)中的衰减因子项2πα,而有阻尼系统的固有频率ωd与式(1)中2πf意义相同,即2πf为系统的有阻尼固有频率,而衰减因子2πα和频率f刚好是本文提出的频谱校正方法所校正出的两个参数,见式(13)和式(15)。由此可见,指数衰减信号的频域插值频谱校正方法可以用来计算欠阻尼情形下的阻尼比及固有频率。

下面给出本文提出的利用指数衰减信号频谱校正方法计算阻尼比的公式。由式(1)和式(19)可知

α=-ζωn/2π

(20)

则有阻尼固有频率ωd和衰减因子α的比值为

(21)

根据式(20)即可求出阻尼比

(22)

式中:fd=ωd/2π为有阻尼固有频率,单位为Hz。

具体计算阻尼比时,首先用指数衰减正弦信号频域插值校正方法获得衰减因子α和有阻尼固有频率fd两个值,代入式(21)即可求出阻尼比ζ和固有频率ωd。然后根据ωd与ωn的关系即可求出系统的无阻尼固有频率为

(23)

2 压电悬臂梁固有频率及阻尼比实验

随着无线传感设备及微机电系统的日益发展,以化学电池为主的供能方式的弊端日渐显露。为实现微机电系统的长时间供能,需要大力发展能量回收技术,将外界能量转换成系统可利用的电能。由于振动现象几乎无处不在且具有较高的能量密度,因此对振动能量的转化及回收利用的研究在近年逐步兴起。目前,振动能量回收技术主要分为静电式、电磁式和压电式3类。其中,压电式方法以其具有的结构简单、不发热、无电磁干扰、清洁环保和易于微型化等诸多优点而得到了极大重视[9-10]。

压电发电装置利用环境中的振动使压电材料发生变形来产生电能,其核心部件是换能器,它决定了系统的能量转换效率[10]。目前,最常用的换能器结构为悬臂梁式结构,如图1所示。换能器设计的一个基本要求是其谐振频率与外界的振动频率一致,使电能输出最大,因此需要对其形状和结构进行优化设计。理论分析压电悬臂梁的电能输出时,将其阻尼设为瑞利阻尼,忽略质量阻尼,而只考虑材料的结构阻尼,此时压电悬臂梁的机电耦合微分方程中的阻尼系数可由阻尼比和固有频率计算得到。

图1 压电悬臂梁结构图

具体实验中,将压电悬臂梁固定在Z型支架上,如图2所示。给其自由端一个微小的瞬时位移激励,然后让其自由振动,利用电涡流位移传感器测量质量块在垂直方向发生的位移量,进而利用该位移量计算求取其固有频率及结构阻尼比。采集信号时,设置采样率为1 000 Hz,从采集信号中截取采样时长为601 ms的数据。图3给出了测得的质量块自由衰减时域曲线和FFT波形图。

图2 压电悬臂梁实验图

3 对比分析

下面分别用时域方法和基于频谱校正的频域方法计算压电悬臂梁的固有频率和阻尼比,并将两种方法进行对比。

3.1 时域方法

时域方法[11-13]是一种简便有效的计算自由振动阻尼比和固有频率的方法。具体来说,分别记录时域曲线上相隔固定周期的几个时刻的位移值,然后利用式(24)计算出系统的阻尼比,根据采集到的信号周期估计出固有频率[10]

(24)

式中:N为计算阻尼比需要的数据点数;τ为相邻两个数据点间所包含的信号周期数。

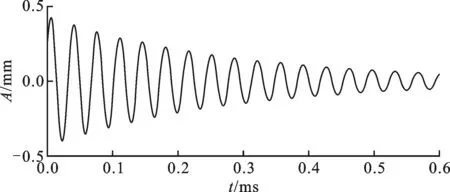
(a)时域波形图

(b)FFT频谱图图3 压电换能器自由衰减时域波形及FFT频谱图

本例中每隔2个周期选择一个数据点,共选择7个数据点,即N=7,τ=2。数据点的位置和对应的位移值分别见图4和表1。

图4 计算阻尼比的7个数据点

使用时域方法,利用7个数据点计算出了6组阻尼比和固有频率。表2给出了使用不同区间的数据的计算结果。

表1 不同数据点的位移

表2 使用不同区间计算出的阻尼比

3.2 基于衰减信号参数估计的频域方法

为了用频域方法计算悬臂梁的固有频率和阻尼比,首先需要用频域插值校正出固有频率和衰减因子的准确值。表3给出了FFT和HDIDFT计算出的信号参数,由于FFT不能计算出衰减因子,因此该项的值为空。

将表3中由HDIDFT计算出的有阻尼固有频率和衰减因子代入式(22),则阻尼比为

表3 信号的FFT和HDIDFT计算结果

(25)

将有阻尼固有频率的值代入式(23),则系统的无阻尼固有频率为

fn=[1-0.01982]-1/2×28.5=28.506 (Hz)

(26)

以上对阻尼比和固有频率的计算结果表明,时域方法和本文提出的利用指数衰减正弦信号频谱校正算法计算系统固有频率和阻尼比的方法具有基本相似的计算结果。本文方法还可应用于多模态的阻尼比的计算中。由于本文方法校正出的固有频率值和衰减因子相对准确,基于二者计算出的参数也较时域方法要准确些。

4 结 论

指数衰减正弦信号广泛存在于机械系统中,因此对该类信号进行分析和参数识别具有重要的理论和现实意义。在分析有阻尼自由振动响应方程的基础上,结合指数衰减正弦信号插值频谱校正技术,本文提出一种利用指数衰减正弦信号频谱校正算法来计算阻尼比和固有频率的新方法,并给出了计算公式。该方法利用校正的信号参数进行计算,从而避免了人工选点造成的主观误差,而通过插值方法校正出的固有频率和衰减因子基本不受采样率的影响,具有较高的估计精度。为了验证该方法的性能,使用其对压电悬臂梁的固有频率和阻尼比进行计算。与传统时域方法相比,本文所提方法适应性更好,精度更高,计算过程也更简单。与传统的频率拟合方法相比,本文所提方法也更简单,计算效率更高。

[1] CHOPRA A K. Dynamic of structures [M]. 2nd ed. Englewood Cliffs, New Jersey, USA: Prentice Hall, 2000: 12-13.

[2] IBRAHIM S R, MIKULCIK E C. Method for the direct identification of vibration parameters from the free response [J]. Shocked Vibration Bulletin, 1977, 47: 183-198.

[3] IBRAHIM S R. An approach for reducing computational requirements in modal identification [J]. AIAA Journal, 1986, 24(10): 1725-1727.

[4] IBRAHIM S R. Random decrement technique for modal identification of structures [J]. Journal of Spacecraft and Rockets, 1997, 14(11): 696-700.

[5] 黄文虎, 夏松波, 刘岩. 设备故障诊断原理、技术及应用 [M]. 北京: 科学出版社, 1997: 53-62.

[6] 周传荣, 赵淳生. 机械振动参数识别及其应用 [M]. 北京: 科学出版社, 1989: 173-176.

[7] 刁瑞朋, 孟庆丰. 一种衰减信号加窗频域插值算法 [J]. 西安交通大学学报, 2013, 47(7): 85-90. DIAO Ruipeng, MENG Qingfeng. Interpolation algorithm for discrete Fourier transforms of weighted damped sinusoidal signals [J]. Journal of Xi’an Jiaotong University, 2013, 47(7): 85-90.

[8] 倪振华. 振动力学 [M]. 西安: 西安交通大学出版社, 1989: 61-69.

[9] 刘祥建, 陈仁文. 压电振动能量收集装置研究现状及发展趋势 [J]. 振动与冲击, 2012, 31(16): 169-176. LIU Xiangjian, CHEN Renwen. Current situation and developing trend of piezoelectric vibration energy harvesters [J]. Journal of Vibration and Shock, 2012, 31(16): 169-176.

[10]王宏金. 基于压电材料的振动能量收集技术及其应用研究 [D]. 西安: 西安交通大学机械工程学院, 2013.

[11]祁泉泉. 基于振动信号的结构参数识别系统方法研究 [D]. 北京: 清华大学土木工程系, 2011.

[12]段志平, 张亚. 结构阻尼识别的方法及比较 [J]. 福州大学学报: 自然科学版, 2005, 33(S1): 208-212. DUAN Zhiping, ZHANG Ya. Structural damping identification methodology and comparison [J]. Journal of Fuzhou University: Natural Science. 2005, 33(S1): 208-212.

[13]李中付, 华宏星, 宋汉文, 等. 用时域峰值法计算频率和阻尼 [J]. 振动与冲击, 2001, 20(3): 7-8. LI Zhongfu, HUA Hongxing, SONG Hanwen, et al. Frequency and damping calculation based on the peak time domain method [J]. Journal of Vibration and Shock, 2001, 20(3): 7-8.

(编辑 武红江)

A New Frequency-Domain Algorithm to Calculate Natural Frequency and Damping Ratio of Mechanical Systems

(School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A new algorithm to calculate the system damping ratio and natural frequency using frequency spectrum correction of exponentially decaying sinusoidal signals is proposed to solve the problem that time domain methods are easy to cause subjective errors and there exists the accuracy limit problem in frequency domain methods in traditional methods to calculate natural frequencies and damping ratios of mechanical systems. The interpolation spectrum correcting method based on Hanning-window is used to obtain frequency deviations and damped factors. Then the natural frequency is calculated by combining similarity relations between damping free vibration responses and exponentially decaying sinusoidal signals, and the system damping ratio and damped natural frequency are obtained. The undamped natural frequency is finally calculated. Both a traditional time domain method and the proposed frequency domain method are respectively used to calculate the natural frequency and damping ratio of a piezoelectric cantilever beam. The results show that the proposed algorithm has a higher calculation accuracy and better adaption of signal to noise ratio. Comparisons with the traditional frequency fitting method show that the new algorithm is simpler and its computational efficiency is higher.

damped signal; frequency spectrum correction; natural frequency; damping ratio; piezoelectric cantilever

2015-03-16 。 作者简介:孟庆虎(1983—),男,博士生;朱永生(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51275380)。

时间:2015-05-21

10.7652/xjtuxb201508001

TN911.72

A

0253-987X(2015)08-0001-05

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150521.0901.001.html