应用基扩展模型的混合信号单通道盲分离算法

熊涛,江桦,崔鹏辉,贾宏雷

(1.信息工程大学信息系统工程学院,450002,郑州;2.解放军65021部队,110000,沈阳)



应用基扩展模型的混合信号单通道盲分离算法

熊涛1,江桦1,崔鹏辉1,贾宏雷2

(1.信息工程大学信息系统工程学院,450002,郑州;2.解放军65021部队,110000,沈阳)

针对传统最小均方误差逐幸存路径处理(LMS-PSP)单通道盲分离算法在时变信道下性能差的问题,提出一种基于基扩展模型逐幸存路径处理(BEM-PSP)的单通道盲分离算法。首先对接收到的部分混合信号进行LMS-PSP单通道盲分离,得到部分准确的信道冲激响应(CIR);然后结合时变信道下基于基扩展模型进行信道估计的思想,完成整个时间周期CIR的估计;最后采用Viterbi算法对混合信号进行序列估计,从而实现时变信道下混合信号的单通道盲分离。仿真结果表明,对于2路混合QPSK信号,在相同仿真条件下,BEM-PSP算法较LMS-PSP算法能降低50%的复杂度且能获得更好的性能,在20 dB处的误码率可达4×10-2,而LMS-PSP单通道盲分离算法的误码率只能达到1×10-1,并且在同等过采样倍数下,该算法能获得更高的性能提升。

单通道;盲分离;逐幸存路径处理;基扩展模型;Viterbi序列估计

在抗干扰通信、信号侦收等领域广泛存在着同频混合信号,该类信号在时频域均发生混叠,不能进行时、频和空域滤波,严重影响了通信质量和信息的提取,而盲分离技术就是处理该类信号的一种信号处理技术,因此具有十分重要的意义,已经成为信号处理领域中的热点问题[1-2]。盲分离是在先验信息未知的条件下根据接收到的混合信号恢复出源信号,如果只有一路接收信号,则称为单通道盲分离。单通道盲分离只有一个已知量,因此在数学上不存在确定解,求解起来十分困难[3],但可以利用信号自身参数上的差异,经过参数差异的提取、放大构造多通道的条件,最终通过多通道技术实现信号分离。如针对不同成形脉冲差异的过采样构造多通道分离算法[4]、针对不同符号速率的小波变换分离算法[5],以及针对不同幅度差异的波形重构抵消分离算法[6]。但是,该类算法性能较差,且易受其余参数的影响,应用受到限制。

通信信号具有有限符号集特征,可以用符号和参数进行准确表示[7],因此充分利用这一特征,将有助于同频混合信号的单通道盲分离。粒子滤波作为非线性非高斯状态估计的一种有力工具,已经用于同频混合信号的单通道盲分离中,它利用联合信道参数估计与序列检测的思想,建立了混合信号的状态方程,进而实现混合信号的分离,取得了较好的分离效果[8-10];然而,由于粒子滤波法复杂度太高,不利于实际应用,文献[11]提出的基于最小均方误差逐幸存路径处理(LMS-PSP)的单通道盲分离算法,将信道参数等效为信道冲激响应(CIR),则只需在序列估计的同时进行滤波器系数更新即可,虽然较粒子滤波算法显著地降低了复杂度,但还是偏高,且在时变信道下该算法的分离性能很差。

本文针对上述问题,提出了基于基扩展模型逐幸存路径处理(BEM-PSP)的单通道盲分离算法,该算法利用时变信道下BEM进行信道估计的思想[12-13],与LMS-PSP算法相结合,完成整个时间周期的信道估计,再进行Viterbi序列检测,从而在时变信道达到降低复杂度而提升盲分离性能的目的。

1 基于BEM的时变混合信道建模

在数字通信中通常存在着反射、折射和衍射,导致接收方不存在直射信号,同时通信双方通常存在着相对移动,则此时的无线信道为典型的多普勒时变信道,而时变信道通常具有窄带特性,BEM信道建模就是利用时变信道的窄带特性,将时变信道转化为少量正交分量的加权线性叠加,其中正交分量表示为BEM的基函数,权值表示为BEM的基系数,而基系数在一定时间周期T内是不变的,这样只需要估计少量的BEM基系数便能较为准确地估计时变信道,从而降低信道估计的计算量,同时尽可能减小了信道衰落对信道估计的影响[14]。

对时间周期内k时刻接收到的同频混合信号按周期Ts/P(Ts为符号周期,P为整数)进行采样,有

(1)

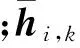
(2)

其中,hi,k+p/P(p=0,1,…,P-1)定义为

hi,k+p/P=[hi,k+p/P(0),hi,k+p/P(1),…,

hi,k+p/P(L-1)]T

(3)

P=1,2…为过采样倍数,表示采样率为符号速率的P倍,k=0,1,…,N-1,i=1,2,N为接收序列符号数,h1,k+p/P、h2,k+p/P为包括成形滤波、信道和接收匹配滤波在内的2路等效CIR,L为信道阶数。

利用BEM算法可以将信道的每一个时变抽头hi,k+p/P(l)(l=0,1,…,L-1)表示为一组时变函数的加权叠加,即

(4)

基函数的选取严重影响着信道估计的性能,常用的基函数有复指数基函数(complex exponential, CE)、多项式基函数和卡洛基函数等,本文综合比较了各种基函数下算法的性能,所采用的基函数为最常见的复指数基函数的改进——泛化过采样复指数(generalized oversampling complex exponential, GOCE)基函数[15],其表达式为

(5)

式中:r=2fd,maxN/(Qfc)为泛化修正系数(fc为载频,fd,max为最大多普勒频移);n为正整数。

2 LMS-PSP单通道盲分离算法

时变信道下混合信号接收模型与文献[11]中的非时变信道下PSK混合信号模型一样,因此在时变信道下可借鉴文献[11]的LMS-PSP单通道盲分离算法进行分离。下面以单倍采样为例介绍LMS-PSP单通道盲分离算法的原理。

LMS-PSP算法的核心是Viterbi算法,是在序列和信道参数组成的联合空间中进行的

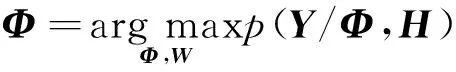
(6)

式中:Φ代表由{φk=(a1,k,a2,k)}组成的符号序列;Y代表由{yk}组成的接收序列;H代表由{h1,k,h2,k}组成的CIR。

假定发送信号均为MPSK调制方式,建立状态图,定义k时刻的状态μk为

μk=(a1,k-L:k,a2,k-L:k)

(7)

在k时刻输入符号对(a1,k,a2,k)时,状态从μk-1转移到μk,同时输出yk,则状态转移可记为

(8)

截止到K时刻,式(6)中的似然概率可写成

p(Y/Φ,H)=p(y0:K|a1,0:K,a2,0:K,h1,0:K,h2,0:K)=

(9)

则k时刻的分支路径度量可定义为

λ(μk-1→μk)=|e(μk-1→μk)|2

(10)

(11)

式中:ai,k(μk-1→μk)是状态转移μk-1→μk对应的第i路信号的符号向量。对每一个状态μk,进行最小化操作来得到累积路径度量

(12)

(13)

式中:γ为步长因子。γ越大,算法的收敛速度越快,但失调系数也越大,故在算法迭代初期选取较大的步长因子来加快收敛,算法迭代后期选取较小的更新步长来减小失调。

PSP算法的核心思想是联合信道估计与序列检测,将信道参数(幅度、相位、时延、频偏等)等效为CIR,这样只要信道参数存在差异,CIR就能区别出来,不存在信号参数的不确定性,而通信中因为发射、接收机的存在,信道参数必定存在差异,故PSP单通道盲分离算法不存在信号参数的不确定性。

3 BEM-PSP单通道盲分离算法

然而,LMS-PSP单通道盲分离算法在时变信道下性能较差。这是因为LMS算法对于时变系统不能进行有效跟踪,同时用LMS算法对CIR进行跟踪时,每个符号分离过程中的CIR估计相当于对CIR进行扩展路径数目次的更新,导致了LMS-PSP算法复杂度较高。本文提出的BEM-PSP单通道盲分离算法的结构如图1所示。

图1 本文的BEM-PSP单通道盲分离算法的结构

由图1可知,本文算法先对前N1(预处理符号数)个接收混合符号进行LMS-PSP单通道盲分离(本文中称为预处理),得到前2N1个CIR的估计,然后将估计出的2N1个CIR当作BEM信道估计的已知值,估计出整个时间周期内的CIR,最后进行Viterbi序列估计,从而完成整个时间周期内混合信号的单通道盲分离。可知,BEM-PSP算法在预处理阶段的复杂度与LMS-PSP算法相同,但在对后N-N1个混合符号处理时,将混合符号分离过程中基于LMS算法的CIR估计替换成基于BEM的CIR估计,LMS-PSP算法中每个混合符号分离过程中的LMS算法的CIR估计相当于对CIR进行扩展路径数目次的更新,为M2倍盲分离状态数(状态数为M2(L-1),M为信号阶数),BEM-PSP算法中每个CIR估计相当于对CIR进行基函数阶数次的更新,而通常情况下预处理符号数N1远小于数据符号数N,基函数阶数小于M2倍盲分离状态数,所以BEM-PSP算法相比于LMS-PSP算法降低了算法的复杂度。

假设信道的初始参数已知,对时变信道下LMS算法的CIR进行跟踪,以信道冲击响应估计的归一化均方误差eCIR为衡量指标,跟踪曲线如图2所示。由图2可见,时变信道下LMS算法的跟踪过程是一个发散的过程,估计的CIR也是一个由准确向不准确逐渐发散的过程。取估计准确的CIR作为BEM信道估计的已知值,进而利用BEM对时变信道估计的优势,从而能较好地完成时间周期内时变信道的估计,所以在时变信道下该算法较LMS-PSP单通道盲分离算法有更好的性能。

图2 时变信道下LMS算法的CIR跟踪曲线

综上,基于BEM-PSP的单通道盲分离算法在复杂度和性能上能较好地解决了LMS-PSP算法的问题。

3.1 基于BEM的信道估计

以单倍采样为例,对长为N的接收序列Y,取前N1个序列Y1={y0,y1,…,yN1-1}进行LMS-PSP单通道盲分离,得到2N1个准确的CIR估计

(14)

式中:i=1,2。将式(14)代入式(2)中可得到该符号周期内基系数的估计

(15)

(16)

3.2 基于BEM-PSP的单通道盲分离算法流程

根据第2节和3.1节原理可知算法流程如下。

步骤1 初始化:设置k=0,初始化信道状态μ0、信道相应h1,k、h2,k,令累计路径度量Γ(μ0)=0。

步骤2 判断:若k≥N1,则运行步骤5;否则,运行步骤3。

步骤3 符号估计:设置k=k+1,输入M2种符号对(a1,k+1,a2,k+1)并从每条幸存路径中扩展分支路径,由式(12)计算其度量λ;然后,根据式(12)对汇聚到每个状态的M2条分支路径计算累积路径度量,保留最好的一条路径。

步骤4 参数更新:根据式(13)对CIR进行更新,并保存此时最优幸存路径上的CIR,转至步骤2。

步骤5 信道估计:根据式(16)对时间周期内的CIR进行估计。

步骤6 符号估计:设置k=k+1,输入M2种符号对(a1,k+1,a2,k+1)并从每条幸存路径中扩展分支路径,由式(10)计算其度量λ;然后,根据式(12)对汇聚到每个状态的M2条分支路径计算累积路径度量,保留最好的一条路径。

步骤7 符号输出:如果k≥m,输出最优幸存路径上存储的(k-m)时刻的符号对(a1,k-m,a2,k-m),其中m为判决延迟。

步骤8 判断输出:若k>N则终止,并输出最后m个时刻最优幸存路径上的符号序列;否则,转至步骤6。

3.3 复杂度分析

对BEM-PSP单通道盲分离算法和LMS-PSP单通道盲分离算法进行复杂度分析,用完成时间周期内接收混合信号单通道盲分离所需的实数乘法和实数加法次数来衡量。

LMS-PSP单通道盲分离算法完成符号分离主要可分为发送序列过信道滤波器、分支路径度量的计算、累积路径度量的计算和基于LMS算法的CIR估计几个阶段,在预处理阶段BEM-PSP单通道盲分离算法与LMS-PSP单通道盲分离算法相同,而在后端处理阶段增加了基于BEM的CIR估计,但减少了基于LMS算法的CIR估计,下面对2种分离算法的计算量进行分析,各个阶段的计算量如表1所示。由表1可知,LMS-PSP算法中LMS信道估计的计算量占整个算法计算量的一半以上,BEM-PSP算法较LMS-PSP算法不同的是将信道估计分为了LMS信道估计和BEM信道估计2部分,因为N1≪N,所以2种算法的计算量受信号阶数的影响,粗略计算可得:当M=2时,2种算法的计算量相当;当M≥4时,基于BEM-PSP单通道盲分离算法的计算量较LMS-PSP算法降低了50%左右,较大地降低了算法的复杂度。

表1 2种分离算法的运算量对比

4 性能分析与仿真

下面通过3个仿真实验,对本文所提算法的性能进行测试。仿真实验模拟信道为幅度服从Rayleigh分布、相位服从均匀分布的Rayleigh衰落信道。将信道的影响等效到2路信号幅度和相位上,即幅度服从Rayleigh分布、相位服从均匀分布。仿真参数设置如下:2信号均采用QPSK调制,接收符号数N=1 000,2路信号的符号周期、载波频率和采样率相同,分别为Ts=1 s、fc=1 Hz和fs=1 Hz,频偏分别为f1=1×10-4Hz、f2=-1×10-4Hz,时延分别为τ1=0.1Ts、τ2=0.4Ts,通信双方相对速度v=180 km/h,n=4,LMS-PSP算法的预处理符号数N1=5,信道阶数L=3,LMS跟踪算法中步长因子γ=0.005,判决延迟m=10Ts,噪声默认为加性高斯白噪声,且信道初始参数已知(或者估计准确),2路信号的幅度与相位如图3所示。

图3 2路信号的幅度与相位

基函数阶数Q的选取也严重影响着信道估计的性能,Q越大基函数矩阵和基系数矩阵维数越大,算法的计算量也越大,但并不是随着Q的增大信道估计的性能就越好,而是在每种情况下都存在一个最优的阶数,其中基函数、符号序列数、最大多普勒频移都是影响Q选取的重要因素。假设初始信道参数设置准确,以CIR的归一化均方误差(NMSE)为衡量指标,图4给出了信噪比为18 dB时不同基函数阶数下的信道估计性能。由图4可知,选取Q=4为最佳阶数。

图4 18 dB时不同基函数阶数下信道估计性能

盲分离后直接得到2路信号的发送符号,由于发送符号存在随机性,故每个仿真实验需重复100次。以分离的2路信号总平均误码率作为本文算法的性能评价指标,估计公式为

(17)

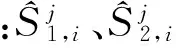
4.1 本文算法与已有算法比较

图5给出了在不同信噪比条件下BEM-PSP算法、文献[11]算法(LMS-PSP)和性能界的误码率曲线,定义整个时间周期CIR已知时算法的误码率作为该条件下的性能界。可以看出,时变信道下本文算法的性能明显优于LMS-PSP算法,但当信噪比增加时2种算法的性能越来越偏离性能界。这是因为:LMS算法收敛速度慢,算法性能随信噪比增加提升缓慢,LMS-PSP单通道盲分离算法整个阶段采用LMS跟踪算法,BEM-PSP单通道盲分离算法在LMS算法的基础上采用更适合时变信道的BEM信道估计算法,而性能界只受噪声影响,信噪比越大性能越好。利用2.4节中2种算法的总计算量公式得出,LMS-PSP算法完成时间周期内符号分离的计算量为2.457 6×108次实数乘法和2.048×108次实数加法,BEM-PSP算法的计算量为9.916 188×107次实数乘法和1.071 081 2×108次实数加法,可见本文算法的复杂度较LMS-PSP算法降低了50%左右。

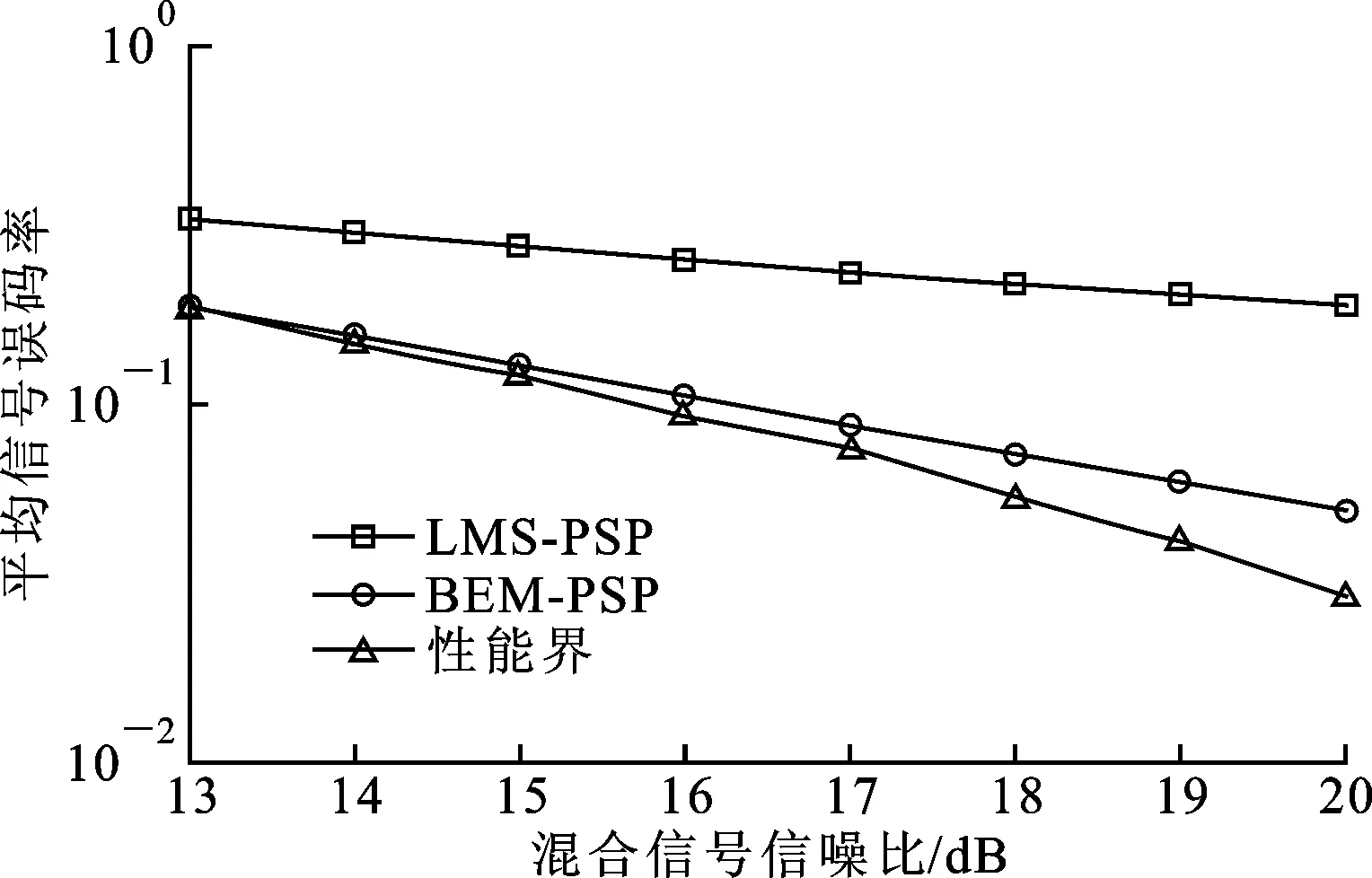
图5 本文算法与LMS-PSP算法的性能比较

4.2 预处理符号数对算法分离性能的影响

由BEM-PSP单通道盲分离算法的原理可知,该算法的分离性能取决于基系数的估计精度,而根据式(15)可知,基系数的估计精度受预处理阶段信道冲激响应的预处理符号数N1和预处理阶段信道冲激响应的精度影响,N1越大,基系数的估计精度越高;预处理阶段信道冲激响应的精度越高,基系数的估计精度也越高。由图2可知,预处理阶段信道冲激响应的N1与预处理阶段信道冲激响应的精度是互相矛盾的,N1越大,预处理阶段信道冲激响应的精度越低,所以BEM-PSP单通道盲分离算法在每种条件下必定会存在一个最佳的预处理符号数,当N1取最佳预处理符号数时,基系数的估计精度最高,算法的分离性能最佳。图6给出了信噪比为18 dB时不同预处理符号数条件下本文算法的误码率曲线,可以看出本文仿真条件下最佳预处理符号数为5,当N1<5时,算法分离性能随着N1减小而变差;当N1>5时,算法分离性能随着N1增大而变差;当N1=5时,算法的分离性能最佳。

图6 18 dB时不同预处理符号数下本文算法的性能

4.3 多倍过采样对算法性能的影响

图7给出了不同过采样倍数下的BEM-PSP算法与LMS-PSP算法误码率比较,过采样倍数取P=1,2,3。可以看出,分离算法的误码率与采样倍数P并不呈线性关系,随着过采样倍数的增加,算法性能提升幅度逐渐降低,但算法复杂度呈线性增加,综合考虑性能与复杂度,一般取过采样倍数P=2已经足够,并且BEM-PSP算法较LMS-PSP算法在同等过采样倍数的情况下能获得更高的性能提升。

图7 不同过采样倍数下几种算法的性能比较

5 结 论

本文重点研究了时变信道下同频混合信号的单通道盲分离问题,将基于基扩展模型的信道估计思想与LMS-PSP算法相结合,提出了一种基于BEM-PSP单通道盲分离算法。与LMS-PSP单通道盲分离算法不同,本文算法不需要在序列估计的同时进行CIR跟踪,而是结合基扩展模型进行信道估计,根据LMS-PSP预处理得到的CIR估计,估计出整个时间周期的CIR,再进行Viterbi序列估计,最终完成混合信号的有效分离。仿真结果表明:对于2路混合QPSK信号,本文所提算法在复杂度减半的情况下性能明显优于LMS-PSP算法,且在同等过采样倍数下比LMS-PSP算法能获得更高的性能提升。

由于时变信道下BEM-PSP单通道盲分离算法性能不是很好,当后端处理对分离性能要求高时,算法将失效,需要研究提升算法性能的方法,如采用判决反馈序列估计(decision feedback sequence estimation,DFSE)、小波去噪(wavelet denoising,WD)等,将是下一步研究的内容。

[1]朱航, 张淑宁, 赵惠昌.基于广义周期性的单通道多分量正弦调频信号分离和参数估计 [J].电子与信息学报, 2014, 36(10): 2438-2444.

ZHU Hang, ZHANG Shuning, ZHAO Huichang.Single channel source separation and parameters estimation of multi-component sinusoid frequency modulation signal based on generalized periodic [J].Journal of Electronics & Information Technology, 2014, 36(10): 2438-2444.

[2]张冬玲, 杨勇, 李静, 等.基于Turbo均衡和信道估计的单通道盲信号恢复算法 [J].通信学报, 2014, 35(1): 47-53.

ZHANG Dongling, YANG Yong, LI Jing, et al.Blind data recovery of single-channel mixed signals based on Turbo equalization and channel estimation [J].Journal on Communications, 2014, 35(1): 47-53.

[3]廖灿辉, 涂世龙, 万坚.抗频偏的突发GMSK混合信号单通道盲分离算法 [J].通信学报, 2013, 34(5): 88-96.

LIAO Canhui, TU Shilong, WANG Jian.Anti-frequency-offset algorithm on single-channel blind separation of burst GMSK mixed signals [J].Journal on Communications, 2013, 34(5): 88-96.

[4]WARNER E S, PROUDLER I K.Single-channel blind signal separation of filtered MPSK signals [J].IEE Proceedings: Radar, Sonar and Navigation, 2003, 150(6): 396-402.

[5]HEIDARI S, NIKIAS C L.Co-channel interference mitigation in the time-scale domain: the CIMTS algorithm [J].IEEE Transactions on Signal Processing, 1996, 44(9): 2151-2162.

[6]毕琰.基于成对载波多址技术的卫星通信关键技术研究 [D].上海: 上海交通大学, 2013: 11-13.

[7]万坚, 涂世龙, 廖灿辉, 等.通信混合信号盲分离理论与技术 [M].北京: 国防工业出版社, 2012: 226-227.

[8]LIU K, LI H, DAI X, et al.Single channel blind separation of cofrequency MPSK signals [C]∥Proceedings of the Fifth AISTED International Conference on Communications, Internet, and Information Technology.Calgary, AB, Canada: Acta Press, 2006: 42-46.

[9]崔荣涛, 李辉, 万坚, 等.一种基于过采样的单通道MPSK信号盲分离算法 [J].电子与信息学报, 2009, 31(3): 566-569.

CUI Rongtao, LI Hui, WANG Jian, et, al.An over-sampling based blind separation algorithm of single channel MPSK signals [J].Journal of Electronics & Information Technology, 2009, 31(3): 566-569.

[10]涂世龙, 郑辉.同频混合信号的一种实时盲解调方案 [J].系统仿真学报, 2009, 21(19): 6203-6206.

TU Shilong, ZHENG Hui.Real-time blind demodulation scheme of co-frequency signals [J].Journal of System Simulation, 2009, 21(9): 6203-6206.

[11]TU S L, ZHENG H, GU N.Single-channel blind separation of two QPSK signals using per-survivor processing[C]∥ Proceedings of 2008 IEEE Asia Pacific Conference on Circuits and Systems.Piscataway, NJ, USA: IEEE, 2008: 473-476.

[12]黄敏, 李兵兵.基于整体最小二乘的联合信道估计及OFDM信号检测算法 [J].电子与信息学报, 2014, 36(6): 1448-1453.

HUANG Min, LI Bingbing.Joint channel estimation and OFDM signals detection based on total least square [J].Journal of Electronics & Information Technology, 2014, 36(6): 1448-1453.

[13]杨小平, 顾亚平, 张俊.基于复指数基扩展模型的抑制Gibbs效应的时变无线信道估计 [J].电子学报, 2013, 41(1): 138-143.

YANG Xiaoping, GU Yaping, ZHANG Jun.Mitigating Gibbs effect time-varying wireless channel estimation based on CE-BEM [J].Acta Electronica Sinica, 2013, 41(1): 138-143.

[14]秦文.OFDM系统中子载波间干扰的产生因素及消除研究 [D].成都: 电子科技大学, 2008: 72-78.

[15]张钦娟, 武穆清, 郭起霖, 等.OFDM系统中优化的泛化复指数基扩展模型 [J].西安电子科技大学学报, 2012, 39(3): 131-135.

ZHANG Qinjuan, WU Muqing, GUO Qilin, et al.Optimized generalized complex exponential basis expansion in the OFDM system [J].Journal of Xidian University, 2012, 39(3): 131-135.

(编辑 刘杨)

A Single Channel Blind Separation Algorithm for Mixed Signals Applying the Base Expansion Model

XIONG Tao1, JIANG Hua1, CUI Penghui1, JIA Honglei2

(1.School of Information System Engineering, Information Engineering University, Zhengzhou 450002, China;2.The 65021th Troop of PLA, Shengyang 110000, China)

A new algorithm based on basis expansion model per-survivor processing (BEM-PSP) is proposed to overcome the poor performance of the traditional least mean square per-survivor processing (LMS-PSP) algorithm for single channel blind separation in time-varying channels.First, a portion of accurate channel impulse response (CIR) is obtained through processing a portion of received mixed signals.Then, estimations of the CIR during the whole time period is accomplished by combining the channel estimation using the basis expansion model.Finally, the Viterbi algorithm is applied to estimate sequences to the mixed signals, and the single channel blind separation of the mixed signals is accomplished.Simulation results and a comparison with the LMS-PSP single channel blind separation algorithm in same simulation conditions show that the complexity of the proposed algorithm reduces by 50% with better performance in processing mixed QPSK signals, and that the proposed algorithm achieves a bit error rate of 4×10-2while the LMS-PSP algorithm only achieves a bit error rate of 1×10-1when the signal to noise ratio is 20 dB.It is also observed that the proposed algorithm obtains a higher performance improvement with the same oversampling ratio.

single channel; blind separation; per-survivor processing; basis expansion model; Viterbi sequence estimation

2014-10-20。 作者简介:熊涛(1990—),男,硕士生;江桦(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61271104)。

时间:2015-03-19

http:∥www.cnki.net/kcms/detail/61.1069.T.20150319.1153.004.html

10.7652/xjtuxb201506010

TN911.7

A

0253-987X(2015)06-0060-07