带有负顾客的M/G/1单重工作休假可修排队系统
2015-12-26牛向阳
张 冕,牛向阳
(阜阳师范学院 数学与统计学院 236037)
带有负顾客的M/G/1单重工作休假可修排队系统
张 冕,牛向阳
(阜阳师范学院 数学与统计学院 236037)
本文考虑了带有负顾客和单重工作休假策略的M/G/1排队系统,其中在正规忙期到达的负顾客带走正在接受服务的正顾客,并且造成系统故障进入修理状态,但修理结束后服务台不能够立刻恢复如新,而是以较低的服务速率进行服务。经过一段随机时间后,才能恢复到正常服务速率。本文给出了稳态条件下系统的顾客队长分布、系统处于各个状态概率和数学期望等一些测度指标。
单重工作休假;负顾客;矩阵分析法
负顾客的排队模型是排队论的一个新兴分支。负顾客通常被认为是一种病毒、一次误操作或者是系统的灾难等等,其主要作用是通过不同的抵消机制对系统产生不同的影响。文献[1-3]考虑了负顾客到达引起服务台故障进入修理期的排队系统,[4]考虑了负顾客到达引起系统服务速率变化。
Servi和Finn[5]提出服务速率可变的工作休假策略,即在休假期间并不完全停止工作,而是以较低的速率为顾客服务。运用拟生灭过程的方法, Li和Tian[6]研究了M/M/1工作休假的排队模型,Li和Ke[7]研究了多服务台单重工作休假M/M/R排队系统。文献[8-9]分别研究了具有工作休假的GI/M/1和GI/M/N排队系统,得到系统在各个时刻的稳态队长及任意顾客逗留时间的分布,Zhang和Hou[10]采用补充变量法研究了工作休假可中止的M/G/1排队模型。上述文献只考虑了服务速率的变化,没有和负顾客结合起来。
本文考虑具有两类顾客到达的M/G/1排队系
统,其中正顾客为正常接受服务的顾客,而负顾客的到达会引起系统故障并进入修理状态,但系统修理结束后服务台不能够立刻恢复如新,而是以较低的服务速率服务一段随机时间后,才能恢复到正常服务速率。
1 模型描述
我们考虑正顾客和负顾客相互独立到达的M/G/1排队系统。正、负顾客的到达过程分别为参数为λ+和λ-的Poisson过程。在正规忙期内服务台以服务速率μb为正顾客服务,如果负顾客到达服务台之前,一旦系统中正到达顾客人数为零,服务台立刻进入工作休假状态;否则进入服务台的的负顾客造成服务台损坏,并且带走正在接受服务的正顾客。服务台损坏后立即进入修理状态,假设修理结束后服务台不能够立刻恢复如新,而是以较低的服务速率μv进行服务,即进入工作休假状态。经过一段随机时间后,才能恢复到服务速率μb,正规忙期开始。如果负顾客到达时,服务台处于空闲、修理或工作休假状态,负顾客立刻离开系统,且对服务台没任何影响。
假设工作休假时间服从参数为的指数分布。在工作休假期间,服务台以较低的服务速率μv服务到达的正顾客;当工作休假结束时,系统中的正顾客人数不为零,服务台立刻将服务速率从μv提高到μb,正规忙期开始;否则,服务台进入空闲状态,等待一个正顾客到达,正规忙期开始。假定顾客按照FCFS排队,并且
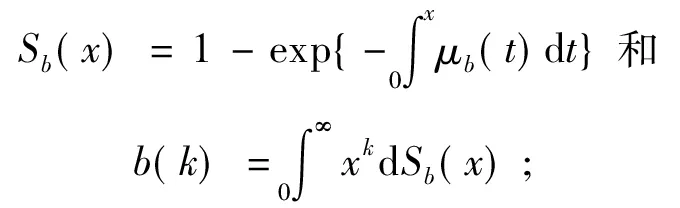

(3)修理时间服从均值为E(R)的一般分布,其分布函数和k阶矩分别为
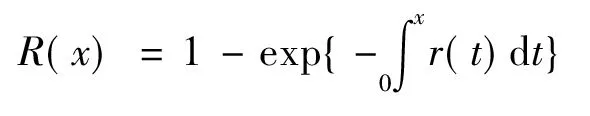

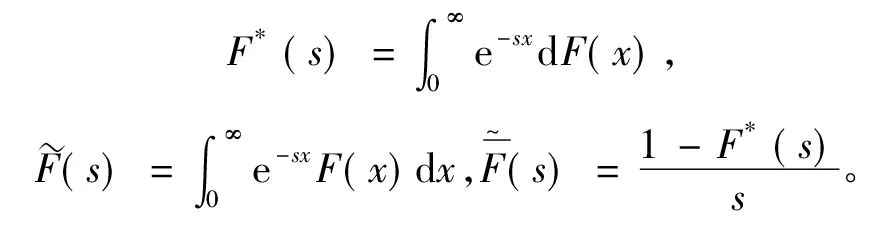
2 马尔可夫链
令N(t)表示系统在时刻的顾客人数,J(t)表示服务台在t时刻所处的状态,J(t)=0,1,2分别对应工作休假期、正规忙期、和修理状态,在ξ0(t),ξ1(t),ξ2(t)分别表示系统在t时刻处于工作休假状态时逝去的服务时间,处于正规忙期时逝去的服务时间以及处于修理状态时逝去的修理时间。显然{J(t),N(t),ξ0(t),ξ1(t),ξ2(t)|t≥0}为Markov链,其状态空间为
Ω={(0,0)}∪{(0,n,x)|n≥1,x≥0}∪{(1,0)}∪{(1,n,x)|n≥1,x≥0}∪{(2,n,x)|n≥0,x≥0}。
定义下列瞬态联合概率
P0(t)=P{J(t)=0,N(t)=0},
Pn(t,x)dx=P{J(t)=0,N(t)=n,
x≤ξ0(t) Q0(t)=P{J(t)=1,N(t)=0}, Qn(t,x)dx=P{J(t)=1,N(t)=n, x≤ξ1(t) Rn(t)=P{J(t)=2,N(t)=n, x≤ξ2(t) 下面我们主要研究系统在平稳状态的概率密度,记 2.1 稳态微分方程组 系统的稳态概率密度{P0,Pn(x),Q0,Qn(x),Rn(x)}满足下列微分方程组 (1-δ1n)λ+Pn-1(x),n≥1 (1) λ+Qn-1(x),n≥1 (2) λ+Rn-1(x),n≥0 (3) 其边界条件为 2.2 平稳条件及微分方程的解 首先给出如下记号 对(1)-(3)式两边分别同乘,并关于n求和得 (10) (11) (12) 解微分方程(8)和(9),得 由部分母函数P(x,z),Q(x,z),R(x,z)的定义,有 为后面处理方便,引入下列记号 且序列{ak|k≥0},{bk|k≥0},{ck|k≥0},{dk|k≥0}及{vk|k≥0}的概率母函数分别为 将代入边界条件,可用矩阵表示为如下 xP=x, 其中x=(P0,Q0,R0(0),P1(0),Q1(0),R1(0),P2(0),Q2(0),R2(0),…), 定理1当时 D(1)V(1)<1,矩阵P为某个正常返不可约马尔可夫链的转移概率矩阵。 矩阵P为一个随机矩阵,是某个不可约马尔可夫链的转移概率矩阵。令 λ+V(1),1+λ+E(R))T。 设矩阵A的不变概率向量为π=(π0,π1,π2),其中 根据Neuts[11],矩阵P是正常返的当且仅当πβ*<1,即ρ<1。 引理1若ρ<1,方程[z-A(z)][z-B(z)]-λ-θzD(z)V(z)C(z)=0在[0,1] 内具有唯一的根z=γ。 证明考虑函数 容易计算得 f(0)>0,f(1)=1,f′(z)≥0,f″(z)≤0, 故方程[z-A(z)][z-B(z)]-λ-θzD(z)V(z)C(z)=0在[0,1] 内具有唯一根,证毕。 将(4)-(8)分别乘上zn并关于n相加得 (13) [z-B(z)]Q(0,z)=θP0z2+θzP(0,z) (14) zR(0,z)=λ-Q(0,z)V(z) (15) 将(15)和(14)式代入(13),得 {[z-A(z)][z-B(z)]-λ-θ D(z)V(z)C(z)}P(0,z) =λ+P0z2[z-B(z)]+λ-θP0z2V(z)C(z)- (16) 在(16)式中,令z=γ,由(4)式,得 (17) =(λ++θ)P0-h(γ)P0 (18) 其中 将(17)和(18)分别代入(13)-(15),得 利用正则条件(9),可以计算出 (19) 其中τ=λ-[λ++θ(1-ρ)]+λ+[θ-h(γ)][1+λ-E(R)]。 综上所述,我们有如下结论: 定理2若ρ<1,稳态下Markov链{J(t),N(t),ξ0(t),ξ1(t),ξ2(t):t≥0}的联合分布函数的部分母函数为 其中P0由(19)式给出。 定理3若ρ<1,平稳状态下系统在工作休假、正规忙期、修理状态下顾客人数的概率母函数为 推论1稳态条件下,服务台处于工作休假、空闲、正规忙期和修理状态的概率分别为 进一步,有交替更新过程以及推论1的结果可以得到稳态下服务台的平均空闲时间、修理时间的平均值以及正规忙期的平均时间,即 本文对具有负顾客到达的单重工作休假M/G/1排队系统进行了研究,得到了稳态条件下系统在任意时刻的顾客队长分布、系统处于各个工作状态的概率和平均时间等性能指标。 [1] Harrison P G, Patel N M,Pitel,E., Reliability modelling using G-queues[J]. European journal of operational research,2000,126:273-287. [2] Wu J B, Lian Z T. A single-server retrial G-queue with priority and unreliable server under Bernoulli vacation schedule[J]. Computers & Industrial Engineering, 2013, 64(1): 84-93. [3] Wang J, Zhang P. A discrete time retrial queue with negtive customes and unreliable server[J]. Computer&Industrial Engnieering, 2009, 56(4): 1216-1222. [4] 岳德权,牛 莉.负顾客到达造成服务率变化的可修排队系统[J].辽宁工程技术大学学报(自然科学版),2012,31(1):102-105. [5] Liu W Y, Xu X L, Tian N S. Stochastic decompositions in the M/M/1 queue with working vacations[J]. Operations Research Letters, 2007, 35(5): 595-600. [6] Servi L D, Finn S G. M/M/1 queues with working vacations (M/M/1/WV)[J]. Performance Evaluation, 2002, 50(1): 41-52. [7] Lin C H,Ke J C. Muti-server system with single working vacation[J]. Applied Mathematical Modelling, 2009, 33:2967-2977. [8] Chae K C, Lim D E, Yang W S. The GI/M/1queue and the GI/Geo/1 queue both with single working vacation[J]. Performance Evaluation,2009,66:356-367. [9] Li J H, Tian N S. Performance analysis of a GI/M/1 queue with single working vacation[J]. Applied Mathematics and Computation, 2011, 217(10): 4960-4971. [10]Zhang M,Hou Z T. M/G/1 queue system with single working vacation[J]. International Journal of Applied Mathematical Computer,2012,29:221-234. [11]Neuts M F. Structured stochastic matrices of M/G/1 type and their application[M], Marcel Dekker, NewYork,1989. An M/G/1 G-queue with server breakdowns and single working vacation ZHANG Mian,NIU Xiang-yang (SchoolofMathematicsandStatistics,FuyangNormalUniversity,FuyangAnhui236037,China) In this paper, an M/G/1 G-queue with server breakdowns and single working vacation is analyzed. A breakdown at busy server is represented by the arrival of a negative customer which causes the customer being in service to be lost. After repair the server is not as good as new until a working vacation time ends. For this model, we firstly obtain the queue length distribution of the customer under the steady state conditions. Then, we give some other performance measures of interest. single working vacation; negative customer; matrix-analytic method 2015-06-20 安徽省高校自然科学研究项目(KJ2015A182,KJ2015A191,KJ2014ZD21);阜阳师范学院科研项目(2015FSKJ07);阜阳师范学院博士科研启动基金资助。 张 冕(1978-),女,博士,教授,研究方向:随机过程、排队论。 O226 A 1004-4329(2015)04-001-05 10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-001-05
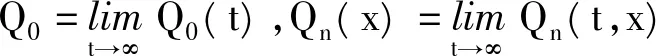


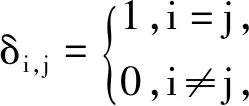




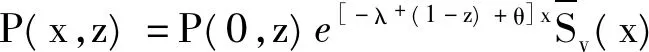

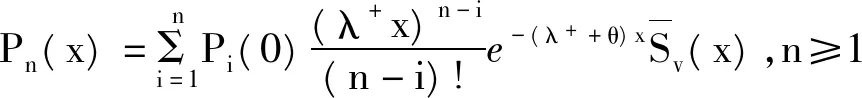
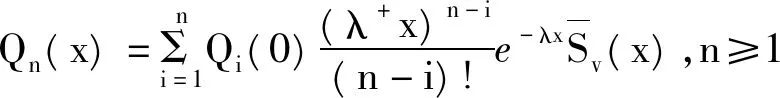











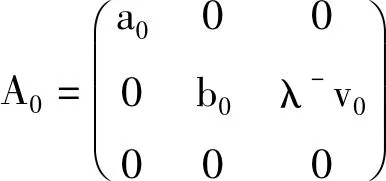
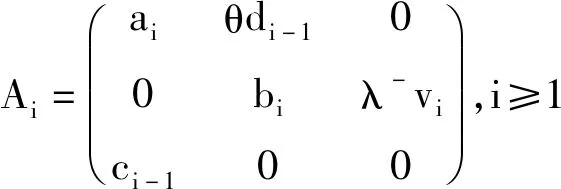


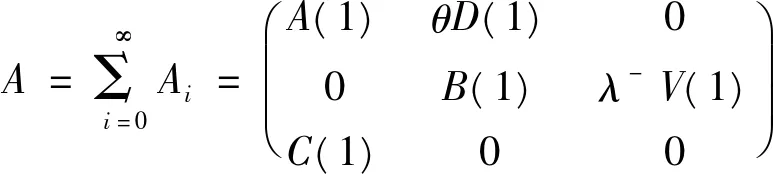



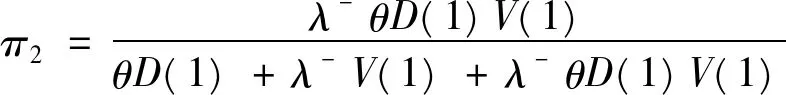

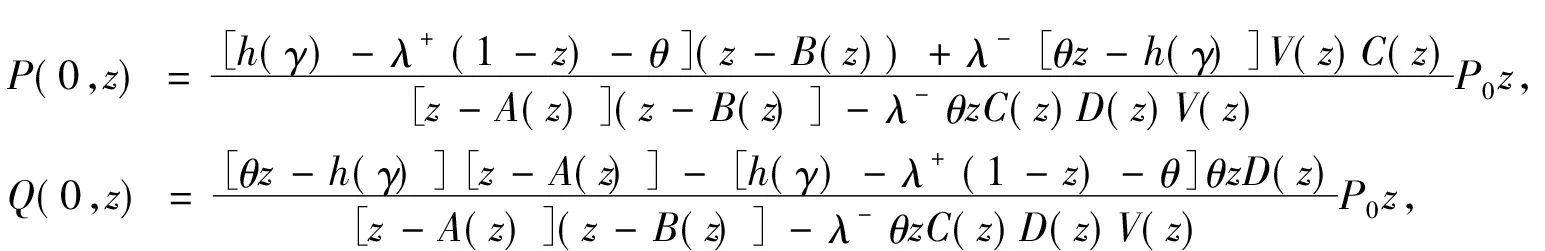

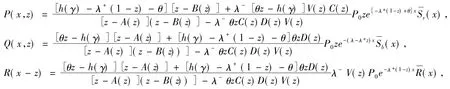
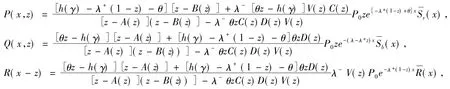
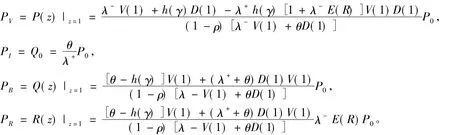
3 结束语
