一种新的连续动作集学习自动机*

2015-12-26刘晓毛宁

数据采集与处理 2015年6期

关键词：高斯分布自动机端点

刘晓毛宁

(中航工业西安航空计算技术研究所，西安，710065)

一种新的连续动作集学习自动机*

刘晓毛宁

(中航工业西安航空计算技术研究所，西安，710065)

学习自动机(Learning automation，LA)是一种自适应决策器。其通过与一个随机环境不断交互学习从一个允许的动作集里选择最优的动作。在大多数传统的LA模型中，动作集总是被取作有限的。因此，对于连续参数学习问题，需要将动作空间离散化，并且学习的精度取决于离散化的粒度。本文提出一种新的连续动作集学习自动机(Continuous action-set learning automaton，CALA)，其动作集为一个可变区间，同时按照均匀分布方式选择输出动作。学习算法利用来自环境的二值反馈信号对动作区间的端点进行自适应更新。通过一个多模态学习问题的仿真实验，演示了新算法相对于3种现有CALA算法的优越性。

机器学习；强化学习；在线学习；学习自动机；连续动作集学习自动机

引言

学习自动机(Learning automation, LA)是一种可应用于未知的、随机环境的自适应决策单元[1-2]。在任一时刻，LA根据某种概率分布从其动作集里选择一个动作，并输出给环境；环境则反馈回一个强化信号，作为对所选动作的评价。根据环境的评价，LA对其概率分布进行调整，以使表现好的动作的被选概率逐渐增大。与有教师指导的监督学习不同，LA采用的是一种强化学习。其中环境并不直接告诉自动机应该选择哪个动作，而只是对自动机选出的每个动作给出一个好或不好的评价，并且这种评价通常都带有一定的不确定性或随机噪声。作为一种有效的机器学习方法，LA已经在许多领域得到了应用，如汽车悬挂控制[3]、数字滤波器设计[4]、噪声容忍模式分类[5]、自适应网页爬取[6]、智能电网中的电源管理[7]、无线传感器网络中的覆盖算法[8-9]以及糖尿病病人最佳胰岛素剂量的确定[10]等。

根据动作集的性质，LA可分为两大类[2]：有限动作集学习自动机(Finite action-set learning automata，FALA)和连续动作集学习自动机(Continuous action-set learning automata，CALA)。 FALA的动作数是有限的，CALA则可以从一个连续区间甚至整个实数轴上选取动作。对于实值参数学习问题，若采用FALA，首先要对动作空间进行离散化。离散化的颗粒度太粗，不能保证结果的精度；太细又会导致动作数过多，学习速度减慢。LA也可以根据环境反馈的强化信号来分类[1]：若强化信号只有两种取值(如用0表示成功，1表示失败)，就称为P型的；若强化信号取值多于两种但又是有限的，则称为Q型的；如果强化信号可取连续的实数值，则称作S型的。上述LA从环境接收的信息只有强化信号。还有一类LA，除强化信号外还可以接收来自环境的状态信息(称为情境输入)。这时，LA的任务是为每一种情境输入选择最适合的输出动作。这种LA被称作联想型LA或者广义学习自动机(Generalized learning automata，GLA)[2]。本文将要研究的是一种P型的、非联想型CALA。

在FALA中，动作概率的表示只需一个维数与动作数相同的矢量即可。但对于CALA，由于有无穷多个动作，动作概率如何表示就成为一个很棘手的问题。故相对于FALA，CALA的研究要困难得多。Gullapalli[11]和Vasilakos等[12]分别提出了可产生实值动作的联想型CALA。这类带有情境输入的GLA，主要用于随机神经网络的学习。目前已知的非联想型的CALA只有以下几种：由Santharam，Sastry和Thathachar提出的模型[13](为区分起见，以下简记为CALA-SST，其中的后缀代表3位提出者名字的首字母)，Beigy和Meybodi提出的模型[14](以下简记为CALA-BM)，Vlachogiannis提出的模型[15](原文作者称其为R-CALA)，以及由Frost，Howell，Gordon和吴青华提出的连续动作强化学习自动机(Continuous action-set reinforcement learning automata，CARLA)[3]。这些CALA都是S型的，其中的环境反馈都可以取连续的实数值。

CALA-SST，CALA-BM和R-CALA都采用高斯分布作为动作选择的概率模型。R-CALA实际上是一种截断高斯分布，因为其动作被限制在一个有限区间上。CALA-SST每次要输出两个动作，一个根据高斯分布随机产生，另一个则直接取高斯分布的均值。算法根据这两个动作以及环境对它们的评价信号，对高斯分布的均值μ和标准差σ进行更新。为防止σ减小到0甚至出现负值，算法引入一个参数σL，使σ不能小于σL。与CALA-SST不同，CALA-BM和R-CALA每次只输出一个动作(按照高斯分布随机产生)。CALA-BM在对高斯分布的均值进行更新时，要求强化信号必须处于0到1之间(如果不在此区间，需先做归一化处理)；R-CALA采用简单的贪婪策略对分布均值进行更新：当所选动作好于迄今最好的动作时，将该动作作为新的均值，否则原均值保持不变。在CALA-BM和R-CALA中，高斯分布的标准差直接根据学习步数来计算，其σ单调减小并最终趋于0。与前面几种CALA不同，CARLA采用非参数化的概率模型，其初始概率分布为一个有限区间上的均匀分布。在学习过程中，算法通过一个对称的高斯型邻近函数，将表现好的动作的奖赏“传播”给其相邻的动作。该算法的实现非常复杂，需要大量的数值积分计算。另外，该算法也需要归一化的强化信号，为此需开辟一个参考存储器以保存环境反馈的历史值。

1 本文提出的CALA

在本文提出的CALA模型中，自动机的动作集对应一个连续区间[xL,xR]，该区间的位置和长度可以动态变化。在任一时刻n，自动机以均匀分布方式从当前区间上随机选择一个动作xn并输出给环境，环境则给出一个二值的评价信号βn∈{0,1}，0表示成功，1表示失败。根据该评价信号，自动机对其动作区间的两个端点进行调整更新。

算法参数：λ1为大于0小于1的常数，控制区间外扩的幅度；λ2为大于0小于1的常数(应小于λ1)，控制区间內缩的幅度；θ为大于0小于1的常数，控制在强化信号为失败的情况下区间端点调整的幅度；ε为足够小且大于0的常数，控制解的精度，并防止区间长度无限缩小。

初始化：给动作区间的左右端点xL和xR分别赋初值，并置n=0。

学习过程：

(1) 按照下式产生一个动作xn，并输出给环境：xn=xL+rn(xR-xL)，其中rn为0到1之间均匀分布的随机数(每次都重新产生)。

(2) 接收环境反馈的强化信号βn。

(3) 更新动作区间(等价于更新概率分布)：令cL=xL+Δ，cR=xR-Δ，其中Δ= (xR-xL)/3；当βn=0时：

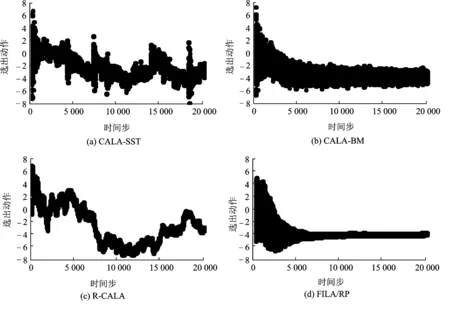
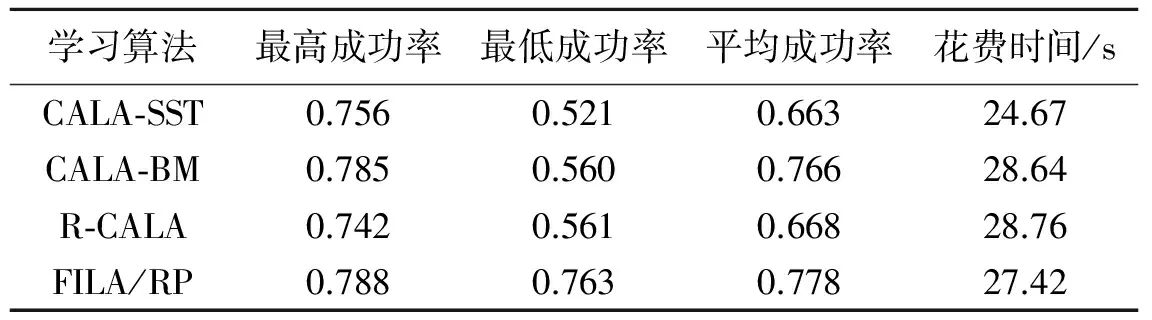
若xn

否则令xL=xL+λ2(1 -ε/Δ)(xn-cL)；

若xn>cR则令xR=xR+λ1(xn-cR)，

否则令xR=xR-λ2(1 -ε/Δ)(cR-xn)；当βn=1时：

若xn

否则，若xn>cR则令xL=xL-θλ1(xn-cL)；

若xn>cR则令xR=xR-θλ2(1 -ε/Δ)(xn-cR)，

否则，若xn

(4) 令n=n+1，转(1)。

上述动作区间更新的基本原理是：先确定区间的左右1/3分界点cL和cR。然后，根据βn的取值情况和xn落于3等分区间的哪一段，对区间的端点进行调整。当βn为成功时，将两个端点均朝xn所在位置的方向移动(奖励xn)；当βn为失败时，若xn落于中间的1/3段，两个端点均保持不变，否则均朝xn所在位置相反一侧的方向移动(惩罚xn)。区间端点移动的幅度与xn跟相应分界点之间的距离成正比，具体的比例系数由参数λ1，λ2，θ和ε控制。其中λ2通常可取λ1/3，以使左端点向右、右端点向左的移动(收缩)比左端点向左、右端点向右的移动(扩张)更谨慎一些。θ的作用是让对失败动作的惩罚比对成功动作的奖励轻一些。

在区间左右移动时，由于两个端点移动的幅度不同，整个区间实际上是扩张的；而当两个端点均向内移动时，区间会收缩。自动机正是通过对其动作区间的自适应调整(可形象地称之为调焦和变焦)，以发现和跟踪最好的动作，将其包围在一个长度逐渐缩小的区间的中心。故将该模型称作“聚焦区间学习自动机(Focused interval learning automaton，FILA)。为体现其对成功的动作进行奖励、对失败的动作进行惩罚的“奖罚”式学习的特点，再在FILA的后面缀以RP，记作FILA/RP。

2 本文算法的分析

(1) FILA/RP选择动作的方法非常简单，只需产生一个均匀分布随机数，并将其映射到当前的动作区间上即可。CALA-SST，CALA-BM和R-CALA则需要产生高斯分布随机数。对于没有现成的高斯随机数函数的场合，则需要通过均匀分布随机数来生成高斯分布随机数，计算量将明显增加。至于CARLA，其动作选择需要计算数值积分，时间开销更大。

(2) FILA/RP对动作区间(对应概率分布)的更新也相当简单，像CALA-SST那样只涉及四则运算，再加一些条件判断。而CALA-BM和R-CALA在计算高斯分布的标准差时，则需要进行开3次方根的运算。CARLA就更加复杂，其对概率密度函数的更新、对概率密度和环境反馈的归一化处理，都需要大量的数值计算。

(3) CARLA需要以离散化的方式存储其概率密度函数，为计算归一化的强化信号还要保存一个滑动窗口内的历史环境反馈值(典型设置为500个)。而FILA/RP则只需保存动作区间的两个端点，存储空间花费非常少。

(4) 在FILA/RP中，当区间左端点向右、或右端点向左移动时，通过因子(1 -ε/Δ)来调节移动的幅度。在学习开始阶段，区间范围宽，ε/Δ很小，(1 -ε/Δ)基本等于1，移动量几乎不受影响；而当区间变得足够窄时，ε/Δ接近于1，(1 -ε/Δ)几乎为0，相应端点的移动量将非常小。这样可防止区间收缩为一个长度为0的“点”，以保持对环境变化进行跟踪的能力(CALA-SST通过引入σL来达到这一点)。而在CALA-BM和R-CALA中，由于高斯分布的标准差单调减小并最终趋于0，自动机将无法发现和跟踪环境的动态变化。

(5) FILA的核心思想是：以一个可变区间作为动作集，按照均匀分布方式产生动作，再根据环境反馈对动作区间的两个端点进行更新。在该框架下，根据环境反馈的性质、是否使用历史信息以及如何使用，可以形成不同的学习算法。本文的FILA/RP是一种P型LA，直接利用环境的二值反馈信号对区间端点进行奖罚式更新。对于环境反馈(即待优化的目标函数)取连续值的情况，则可以记忆历史目标函数值，利用其中“最新”且“最好”的动作对区间进行“奖励”式更新，这样可以得到S型的学习算法。

3 仿真实验和结果分析

现在考虑这样一个随机学习问题，其中动作参数x可在(-∞,∞)上连续取值。对于每个x,环境都会给出一个二值的强化信号β(x)，其中β(x)以d(x)的概率取0(表示成功)，以1-d(x)的概率取1(表示失败)。不同动作参数的成功概率由下式确定

(1)

这是一个多模态的非线性函数，在点-4和4处各有一个高度约为0.8的峰值，在x等于0处则有一个高度约为0.47的“波谷”。在±4之外、随着x绝对值的增大，d(x)逐渐减小并趋近其下限0.4。分别利用FILA/RP和3种基于参数化概率模型的CALA，即CALA-SST，CALA-BM和R-CALA对上述问题进行仿真实验。CALA-SST的内部参数[5]经反复尝试选取如下的效果相对好的数值：λ=0.008，K=0.7，σL=0.02；高斯分布的初始参数取μ0=0，σ0=5。关于CALA-BM，文献[14]指出可根据σn=1/[floor(n/10)]1/3来计算n时刻高斯分布的标准差，其中floor为下取整函数。显然，当n<10时该式会出现除法溢出。为此，floor替换为向上取整函数ceil。但即使这样，算法仍不能较好地工作，原因是σn衰减过快。因此对该算法再次进行了“改造”，即像CALA-SST那样，引入一个新的参数σ0，并按照σn=σ0/[ceil(n/10)]1/3计算n时刻高斯分布的标准差，使得σn的衰减速度可以被控制。CALA-BM的内部参数，学习步长a取0.015，新引入的σ0取5；高斯分布的初始均值μ0取0。原始的R-CALA算法[15]，保存β的全程最小值βmin，当βn<βmin时将对应的xn赋给μn同时更新βmin。由于本文的β只有0和1两种取值，若采用该规则，μn和βmin最多只能被更新一次，无法实现学习。故在本研究中，以″≤″取代″<″。R-CALA只有两个内部参数：动作参数的上、下限xmax和xmin，仿真中分别取7和-7。对于FILA/RP，相关参数设置如下：θ=0.1，ε=0.02，λ1=3λ2且λ2=0.01；初始动作区间取为[-5,5]。每次仿真均运行20 000步。图1给出的是4种算法各7次仿真过程中，动作空间的中心(对FILA/RP来说就是动作区间的中点，对另外3种算法来说则是高斯分布的均值)随仿真时间n的演化轨迹。

图1 动作空间的中心随仿真时间的变化轨迹(每种算法各仿真7次)Fig.1 Center of action space vs.time step(7 simulations per algorithm)

由图1可以看出，CALA-SST和R-CALA的高斯分布均值的演化轨迹非常杂乱，到仿真时间结束时(n=20 000)，仍有部分μn未能稳定于最优解-4或4。相比之下，CALA-BM则好很多，7次仿真全都能收敛到两个最优解之一。不过，CALA-BM有一条μn曲线向目标靠近的速度相当缓慢。这是由于其高斯分布的标准差σn衰减相对较快，限制了μn的移动速度。增大新引入的参数σ0，可以加快μn移动的速度，但算法选择动作时的目标将不再集中，自动机选出的xn的波动将会增大。4种算法中，表现最好的还是FILA/RP，其动作区间的中心全都能很快移动到两个最优解之一。

图2给出的是每种算法一次典型的仿真中，自动机选出的动作序列xn的演化轨迹。在图2所示的仿真中，4种算法基本上都发现了最优动作-4，但不同算法的运行轨迹却有很大的差异。FILA/RP和CALA-BM均能较快地定位目标，然后坚守，它们找到目标后的动作轨迹都很笔直。不过，CALA-BM的轨迹要臃肿和粗糙得多，这表明其目标不够集中，选择的动作有较大的波动。减小新引入的参数σ0，可以使轨迹变细，但这又会导致μn的移动变缓(正如图1(b)中的那条移动缓慢的曲线)。再看CALA-SST和R-CALA，二者的动作轨迹都相当曲折，很难稳定在最优解上。另外，CALA-SST的动作轨迹上有一些明显的、几乎垂直分布的突跳点，这是由于其高斯分布的标准差变化剧烈，突然间增大，随即又快速变小。相比之下，FILA/RP的表现最好，其先通过调整动作区间的端点，将最优解包围在区间的中心，然后再使区间迅速收缩，此后则基本上只在该最优解的一个很小的邻域内选取动作。

图2 一次典型仿真中自动机选出的动作随时间的变化轨迹Fig.2 Action selected by LA vs. time step in typical simulation

为评估每种算法的在线学习性能，在仿真过程中的每一步，都计算截止当前自动机实际获得的成功率Rn=sn/n，其中sn为到n时刻的累计成功次数。这样，每做一次仿真，就会得到一条Rn曲线。由d(x)的定义不难知道，Rn的理想的变化轨迹是逐渐逼近0.8(理论最大成功概率)。由于LA本质上是一种由随机数序列驱动的随机搜索算法，每次运行不一定能得到相同的结果，故为全面、客观地评估各算法的性能，对每一种算法各做了200次仿真。图3给出的是每种算法200次仿真中Rn曲线叠加在一起的效果。

由图3可以看出，3种现有算法的学习轨迹都很散乱(尤其是CALA-SST和R-CALA)，这表明它们对随机数序列很敏感，算法每次运行结果的一致性很差。仔细观察不难发现，各算法的行为表现还存在一些细节上的差异。在学习初期，CALA-SST反应较为迟钝，Rn上升缓慢。R-CALA的某些Rn，从一开始就处于相当高的水平(不过后面并没有进一步上升)；但又有一些Rn却几乎一直呆在很低的水平上(CALA-SST也一样)。到仿真时间结束时，CALA-SST和R-CALA的Rn都非常分散，分布范围很宽。至于改造后的CALA-BM，有一些仿真相当不错，最好的结果显著好于前两种算法；但另一些则不好，Rn上升缓慢，其中最差的一个在仿真结束时只到0.56。相比之下，FILA/RP的学习轨迹则显得相当紧凑，上升趋势也很清晰，到仿真结束时其成功率全都集中于一个很窄的范围之内。表1给出了4种算法各200次仿真(每次仿真20 000步)的相关统计结果。

由表1不难看出，FILA/RP的最高、最低和平均成功率在4种算法中都是最好的，其最差结果不仅远远好于3种现有算法的最差结果，甚至比CALA-SST和R-CALA的最好结果还要好，快赶上经改造的CALA-BM的平均结果了。FILA/RP性能优异的根本原因，在于其独特的概率模型和模型参数的更新机制。在现有的采用参数化概率模型的CALA-SST，CALA-BM和R-CALA中，高斯分布的均值和标准差分别进行更新或计算，容易造成分布位置和宽度的脱节，使得均值尚未移动到理想位置、方差就已经很小，或者方差衰减过慢、算法迟迟不能收敛。FILA/RP对区间端点的更新，则同时实现了区间位置和宽度的调整，其目标的准确度和集中度得到很好的统一。CALA-SST和R-CALA表现不好还有一个原因，二者都基于对环境反馈(β)的比较来更新高斯分布的均值。对于环境反馈只有0和1两种取值的P型环境，这种比较不能给算法提供足够的信息。

在算法的运行时间方面，CALA-SST耗时最少，其次是FILA/RP。CALA-BM和R-CALA在确定高斯分布的标准差时都要计算三次方根，时间花费较长。在本文的仿真中，高斯随机数均通过调用Matlab的randn函数产生。如果通过自编程序产生，则3种现有算法的耗时都将显著加长。

图3 在线学习性能(每种算法各仿真200次)Fig.3 Online learning performance(200 simulations per algorithm)

学习算法最高成功率最低成功率平均成功率花费时间/sCALA⁃SST0．7560．5210．66324．67CALA⁃BM0．7850．5600．76628．64R⁃CALA0．7420．5610．66828．76FILA/RP0．7880．7630．77827．42

4 结束语

为解决备选动作取实数值的强化学习问题，本文提出一种新的连续动作集学习自动机，即基于奖罚式学习的聚焦区间学习自动机(FILA/RP)。该自动机的动作集为一个实数区间，通过均匀分布方式选择输出动作，并根据环境反馈对区间的端点进行自适应调整。跟现有的CALA相比，本文的FILA/RP有一些显著的特点和优势。现有的CALA都是S型的，即环境反馈可以连续取值，FILA/RP则是P型的，因而更适合具有二值反馈的随机环境。FILA/RP采用一种特殊的参数化概率模型，学习过程中需要存储和更新的参数只有两个(即区间的两个端点)，这使得与采用非参数化概率模型的CARLA相比，该算法的实现非常简单，时间和空间开销都很小。现有的参数化CALA在选择动作时，都需要高斯分布随机数，新算法则只需要均匀分布随机数，其产生更为容易。由于动作区间不会无限收缩，FILA/RP可以跟踪环境的动态变化；CALA-BM和R-CALA则不能，因为它们的高斯分布的标准差只能单调减小并最终变为0。通过一个多模态的实值参数强化学习问题的仿真实验，演示了新算法的优异性能。与3种现有的参数化CALA相比，本文提出的FILA/RP具有学习速度快、精度高和运行结果的一致性好等优点。目前，已将该算法应用于联想强化学习问题，其效果仍然好于现有的CALA(相关内容将另文发表)。进一步研究的方向，包括用更多、更复杂的问题对该算法的学习性能进行测试和评估，以及尝试将其应用于模式识别、智能控制等实际工程领域。

[1] Narendra K S,Thathachar M A L.Learning automata：An introduction[M].Englewood Cliffs,NJ：Prentice Hall,1989：35-58.

[2] Thathachar M A L，Sastry P S.Varieties of learning automata：An overview[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B：Cybernetics,2002,32(6)：711-722.

[3] Howell M N,Frost G P,Gordon T J,et al.Continuous action reinforcement learning applied to vehicle suspension control[J].Mechatronics,1997,7(3)：263-276.

[4] Howell M N,Gordon T J.Continuous action reinforcement learning automata and their application to adaptive digital filter design[J].Engineering Applications of Artificial Intelligence,2001,14(5)：549-561.

[5] Sastry P S,Nagendra G D,Mamwani N.A team of continuous-action learning automata for noise-tolerant learning of half-spaces[J].IEEE Transactions on Systems,Man,and Cybernetics，Part B：Cybernetics, 2010,40(1)：19-28.

[6] Torkestani J A.An adaptive focused web crawling algorithm based on learning automata[J].Applied Intelligence,2012,37(4)：586-601.

[7] Misra S,Krishna P V,Saritha V,et al.Learning automata as a utility for power management in smart grids[J].IEEE Communications Magazine,2013,51(1)：98-104.

[8] Mohamadi H,Ismail A S,Salleh S.Solving target coverage problem using cover sets in wireless sensor networks based on learning automata[J].Wireless Personal Communications,2014,75(1)：447-463.

[9] 王建平,陈改霞，孔德川，等.一种基于学习自动机的WSN区域覆盖算法[J].数据采集与处理，2014,29(6)：1016-1022.

Wang Jianping,Chen Gaixia,Kong Dechuan,et al.Learning automata-based area coverage algorithm for wireless sensor networks[J].Journal of Data Acquisition and Processing,2014,29(6)：1016-1022.

[10]Torkestani J A,Pisheh E G.A learning automata-based blood glucose regulation mechanism in type 2 diabetes[J].Control Engineering Practice,2014,26：151-159.

[11]Gullapalli V.A stochastic reinforcement learning algorithm for learning real-valued functions[J].Neural Networks,1990,3：671-692.

[12]Vasilakos A,Loukas N H.ANASA—A stochastic reinforcement algorithm for real-valued neural computation[J].IEEE Transactions on Neural Networks,1996,7：830-842.

[13]Santharam G,Sastry P S,Thathachar M A L.Continuous action set learning automata for stochastic optimization[J].Journal of the Franklin Institute,1994,331B(5)：607-628.

[14]Beigy H,Meybodi M R. A new continuous action-set learning automaton for function optimization[J]. Journal of the Franklin Institute,2006,343(1)：27-47.

[15]Vlachogiannis J G.Probabilistic constrained load flow considering integration of wind power generation and electric vehicles[J].IEEE Transactions on Power Systems,2009,24(4)：1808-1817.

New Continuous Action-set Learning Automation

Liu Xiao, Mao Ning

(Xi'an Aeronautics Computing Technique Research Institute，AVIC，Xi'an，710065，China)

Learning automaton (LA) is an adaptive decision maker that learns to choose the optimal action from a set of allowable actions through repeated interactions with a random environment. In most of the traditional LA, the action set is always taken to be finite. Hence, for continuous parameter learning problems, the action space needs to be discretized, and the accuracy of the solutions depends on the level of the discretization. A new continuous action-set learning automaton (CALA)is proposed. The action set of the automaton is a variable interval, and actions are selected according to a uniform distribution over this interval. The end-points of the interval are updated using the binary feedback signal from the environment. Simulation results with a multi-modal learning problem experiment demonstrate the superiority of the new algorithm over three existing CALA algorithms.

machine learning; reinforcement learning; online learning;learning automata; continuous action-set learning automata

2014-06-05；

2014-06-30

TP181；TP202.7；O234