基于灰关联混合蛙跳算法的雷达波形设计*

2015-12-26龙伟军龚树凤韩清华

数据采集与处理 2015年6期

关键词：蛙跳模因适应度

龙伟军龚树凤韩清华商妮贲德

(1.南京航空航天大学雷达成像与微波光子技术教育部重点实验室，南京，210016； 2.南京电子技术研究所，南京，210039)

基于灰关联混合蛙跳算法的雷达波形设计*

龙伟军1,2龚树凤1韩清华1商妮1贲德1,2

(1.南京航空航天大学雷达成像与微波光子技术教育部重点实验室，南京，210016； 2.南京电子技术研究所，南京，210039)

提出了一种基于灰关联混合蛙跳算法的雷达波形设计方法，以混合蛙跳算法为主体，在局部更新算子中引入遗传算法的遗传算子，并改进原始蛙跳算法的分组方法，丰富了种群的多样性，同时引入灰关联综合评价法则对适应度函数值加以关联度分析。文中以设计具有低自相关旁瓣和互相关特性的正交多相编码为例，将该算法用于雷达波形设计中。仿真结果表明使用本文算法产生的波形具备较好的低自相关特性和互相关特性，表明了该算法是有效和可行的。

混合蛙跳算法；遗传算子；分组方法；灰关联评价；正交波形

引言

雷达发射波形的设计对信号的处理方法、系统的分辨力、量测精度以及抗干扰能力等性能有直接的影响，具备优良特性的波形可以促使雷达充分发挥其潜在性能。近几年，现代智能优化理论的快速发展为雷达波形的设计注入了新的活力，并广泛应用于雷达波形参数的选择中。Deng基于模拟退火算法(Simulated annealing algorithm，SA)分别设计了可用于组网雷达系统的正交多相编码序列、离散频率编码序列，仿真实验表明基于模拟退火算法设计的编码序列具有较好的自相关和互相关特性[1-2]。陶海红基于梯度搜索和遗传算法相结合的混合遗传算法，设计了m-序列二相编码脉冲压缩波形，仿真结果表明所设计的波形具有优越的性能，且该算法具有更快的收敛速度[3]。文献[4]结合hamming扫描和模拟退火算法，提出了一种改进的模拟退火算法，该算法同时具有模拟退火算法的全局最优性能和hamming扫描收敛速度快的优点，可以设计出具有更好自相关和互相关性能的波形。文献[5-7] 针对多输入多输出(Multiple input multiple output,MIMO)雷达，利用遗传算法(Genetic algorithm，GA)对可用于 MIMO 雷达的正交波形进行了优化设计，仿真结果表明了该算法设计正交相位编码和离散频率编码信号的有效性。文献[8]将模拟退火算法和遗传算法结合在一起，并引入灰关联度综合评价对适应度函数进行综合评判，设计了性能优良的多相编码波形，但计算时间略长。文献[9]在离散频率编码波形信号模糊函数的基础上，建立波形优化模型，将微群粒子群优化算法(Micro particle swarm optimization，MicPSO)应用于离散频率偏码波形(Discrete frequency coding waveform，DFCW)设计，结果表明该方法时间开销小，优化结果理想。但这些优化算法都是从单个个体开始对整个群体进行搜索更新，算法的复杂度高，执行效率低。此外，文献[10]将混沌理论引入到MIMO雷达的正交波形设计中，设计了混沌序列的调频编码波形，并得到了良好的性能。

2001年，国外学者Eusuff和Lansey提出了混合蛙跳算法(Shuffle frog leaping algorithm, SFLA)[11]，该算法模拟青蛙觅食的过程，通过分组算子和模因组融合成群体的机制来传递信息，再将全局的信息交换与局部搜索相结合来寻优[12]。其中，局部搜索使得局部个体间的信息得以传递，而混合策略则使得模因组间的信息能够进行交换。该算法的搜索过程是从一个解集合开始，而不是从单个个体开始，不容易陷入局部最优解，具有并行性，易于在并行计算机上实现，从而提高算法的性能和效率。同时，由于每次进化只对最差青蛙进行调整，所以算法具有快速收敛、容易操作、小计算量、鲁棒性强以及不易陷入局部最优等良好性能，目前主要用于解决多目标优化等问题。Eusuff等第一次使用该算法解决扩充管道网络时使得管道尺寸最小化的问题，并由此提出了新的计算模型混合蛙跳算法网络(Shuffle frog leaping algorithm network,SFLANET)[13]；随后，Elbeltagi等对几种不同的进化算法进行了比较，其中包括遗传算法、模因算法(Memetic algorithm, MA)、粒子群算法(Particle swarm optimization,PSO)、蚁群算法(Ant colony optimization, ACO)和SFLA，通过实验发现，在面对某些连续函数的问题时，SFLA在求解时代收敛速率以及成功率比GA要高，与PSO相近似[14]。此外，还有诸多学者提出了一些方法对蛙跳算法进行改进，如将一个参数引至最初的蛙跳算法中以便加速搜索范围[15]；将PSO中的惯性移动与SFLA的子群相结合，从而生成新的MA算法[16]；还有学者引进了认知控件，该控件用来代表每只青蛙的思想，以此来增强算法的性能，如稳定性以及全局的搜索能力等[17]；此外，增加阈值选择策略，利用更新不满足阈值条件的个体分量，降低个体在空间中的差异性来增强算法的性能[18]。

本文以原始的蛙跳算法为基础，在分组进化时与遗传算法相结合，同时对原始蛙跳算法的分组方法加以改进，使得每个模因组不再是适应度值较差的个体，丰富了种群的多样性。同时考虑到适应度函数是评价波形的各项指标及指标权重的函数，其值是综合体现的结果，而引入了灰关联综合评价法则，综合比较个体的适应度值。并以雷达正交多相编码波形为例，选取自相关和互相关特性值为适应度函数，利用改进的混合蛙跳算法对波形进行优化设计。最后的仿真结果表明，该算法可行且高效。

1 正交相位编码波形设计原理

假如雷达在某种场合下有L个发射单元工作，每个单元发射的波形码长为N，相位编码个数为M，则第l个信号可表示为

(1)

编码相位取为

(2)

整个码组信号矩阵可表示为

(3)

正交信号的自相关函数和互相关函数应满足如下两个条件

(4)

式中：l=1,2,…,L。

(5)

式中：p≠q;p,q=1,2,…,L。

联合码组信号矩阵可得

(6)

式中：l=1,2,…,L。

(7)

式中：p≠q,p,q=1,2,…,L。

综合考虑信号自相关特性和互相关特性的要求，正交多相编码的设计实则就是在约束条件下构造最优矩阵的问题。对此问题进行求解，通过最小化目标函数寻求最优相位序列不失为一种有效的方法。设计正交相位编码信号时，目标函数应该考虑到自相关函数旁瓣峰值和互相关峰值，为了防止峰值过高，还应考虑到自相关旁瓣能量和互相关能量，因此将目标函数表示为

(8)

2 基于灰关联混合蛙跳算法的正交多相编码设计

2.1 混合蛙跳算法的基本原理

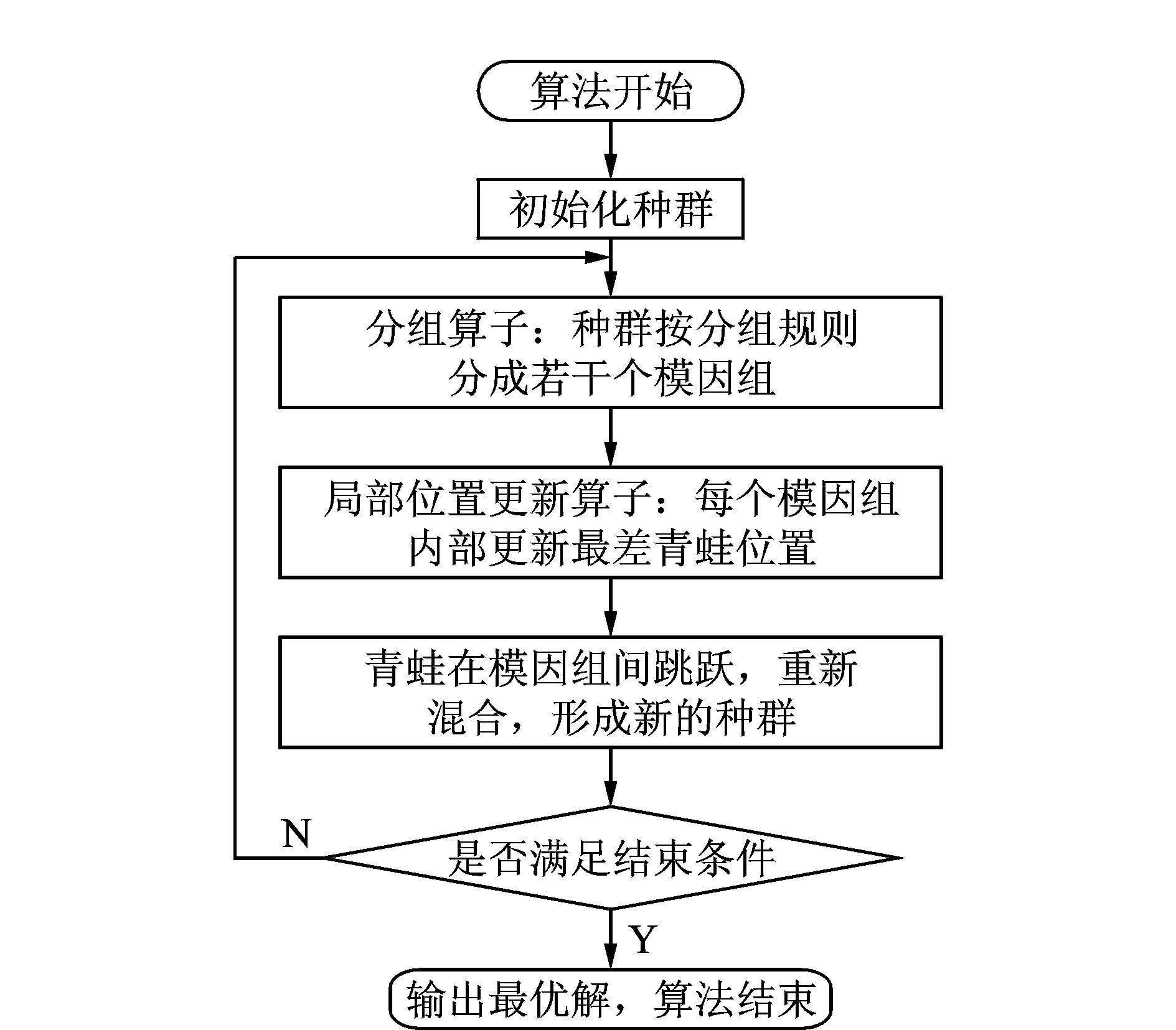
图1 混合蛙跳算法流程图Fig．1 Flow chart of shuffle frog leaping algorithm

混合蛙跳算法作为一种智能化寻优算法，其实现原理是通过模拟自然世界中青蛙群体在寻找食物过程中所表现出来的相互合作以及交互信息等行为，来对所求问题进行求解。其中，定义每只青蛙个体代表问题的一个解。整个青蛙群体采用模因分组方法分为不同的子群体，来模拟青蛙的聚群行为，每个子群体称为模因分组。模因组中的每只青蛙都有为了靠近目标而努力的想法，具有对食物源远近的判断能力，并且受其他青蛙的影响，可以称之为文化。每个模因组都有自己的文化，影响着其他个体，并随着模因组的进化而进化。在模因组的每一次进化过程中，在每个模因组中找到组内位置最好和最差的青蛙。组内最差青蛙采用类似于粒子群算法中的速度位移模型操作算子，执行局部位置更新，对最差青蛙位置进行调整。模因组内经过一定次数的模因进化后，将不同模因组间的青蛙进行混合，重新组成新的整个群体，以此来实现信息在各个模因组间的交流与共享，直到算法满足预先定义的收敛条件为止。基本的混合蛙跳算法流程图如图1所示。

2.2 混合蛙跳算法在波形设计中的应用

2.2.1 算法术语

混合蛙跳算法中，每只青蛙为一个单独的个体，在算法中作为问题的一个解。一定数量的青蛙个体组合在一起称为青蛙群体，群体中的个体数目总和称为群体规模，又叫群体大小。将青蛙群体分为若干个小的群体，每个青蛙子群体称为模因分组。食物源为青蛙要搜索的目标，在算法中体现为青蛙位置的最优解。适应度代表的是青蛙对环境的适应程度，通过青蛙距离目标解的远近来表示。混合蛙跳算法根据分组算子的规则，把整个种群分为若干模因组，在每个模因组中最差青蛙位置的更新与调整的策略称为局部位置更新算子。

在雷达波形设计中，将每个编码序列看作青蛙个体，序列的集合称为青蛙群体，群体中序列数目的总和叫群体规模，将序列集合划分为多个子序列集合称为模因分组，最优编码序列为青蛙的食物源，适应度为编码序列的自相关和互相关特性值。

2.2.2 灰关联综合评价法则

灰关联综合评价也可称为灰关联多目标决策，结合了灰色系统理论[19]和多目标决策两个方面，按照决策方案中更多定性了解的灰色信息来解决多目标决策问题，在工程技术和军事系统等领域中有着广泛的应用[20-21]。

利用遗传算法设计正交多相编码波形，引导算法搜索方向的主要依据是个体的适应度值，而适应度值是波形自相关旁瓣峰值、互相关峰值、自相关能量和互相关能量等各指标以及指标权重综合的结果，用适应度函数表示。因此，适应度函数是个多目标优化的问题，为了能够反映不同指标要素对适应度值的影响，采用灰关联度对适应函数进行优劣比较，个体适应度值的关联顺序反映了个体对最佳个体的接近顺序，其中关联度最大的个体就是最优解。下面对其建立模型，主要分为4个步骤：

(1) 初始决策矩阵构建

设X为要决策的个体集合，也称之为目标域集合，Y为指标要素的集合，指标要素的加权向量为W，则有如下表述：

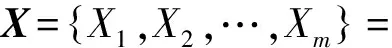
个体Xi对指标Yj的属性值记为Aij(i=1,2,…，m,j=1,2,…，n)。针对所包含的各指标信息，采用定性分析的方法，可以将其分为“越大越优类型”指标(又称为正指标)和“越小越优类型”指标(又称为负指标)。将目标域集合与指标要素相结合以构成初始的决策矩阵A0。本文中，代价函数考虑自相关旁瓣峰值、自相关能量、互相关峰值以及互相关能量4个指标，即n=4，希望4个指标都是越小越好，因此为“越小越优类型”指标。

(9)

(2) 评价指标确定

根据初始的决策矩阵A0，依照各指标要素相应的优化准则，选出各指标要素之间相对的最佳值形成最优的参考序列并将其视为最佳的评价方案；按照各指标要素相应的劣化准则，选出各指标要素之间相对的最劣值形成最劣的参考序列并将其视为最差的评价方案。根据上述准则可以获得最优的参考序列为列Xg=(Xg1,Xg2,Xg3,Xg4)，Xgi=min(A1i,A2i,…，Ami)；最劣参考序列Xb=(Xb1,Xb2,Xb3,Xb4)，Xbi=max(A1i,A2i,…，Ami)。

(3) 灰关联度计算

① 无量纲化处理

由A0和Yg组成最优灰关联决策矩阵A。在计算之前首先要对A进行无量纲化处理，即用每个指标的属性值除以相应的指标参考序列值。

(10)

② 灰色关联系数

分别求出每个指标序列的序列差。无量纲化后的最优序列为{1,1,1,1}，计算灰色关联系数如下式

(11)

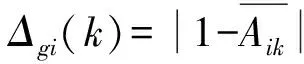
(12)

③ 灰色关联度

为反映不同指标要素对综合评价的影响，引进权重向量，则根据权重向量和灰色关联系数可以求得灰色关联度为

按照同样方法求得与最劣参考序列的灰关联度γbi。

(4) 灰色关联综合评价

假设个体i与最优、最劣两个参考序列之间的灰色关联度依次为γgi和γbi，若两者的排列顺序是完全相逆的，则说明个体i与最优参考序列之间的灰色关联程度等同于与最劣参考序列之间的非关联程度。但如果γgi和γbi的排列次序不是完全相逆的，则很难进行个体选择，因此运用灰色综合评价模型进行个体选择是十分有必要的。

假设vi表示个体i与最优参考序列之间的从属值，则与最劣参考序列之间的从属值记为(1-vi)，并称(1-vi)为个体i的优偏离度，vi为个体i的劣偏离度。则根据目标函数

(13)

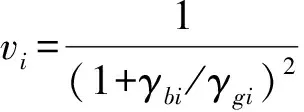
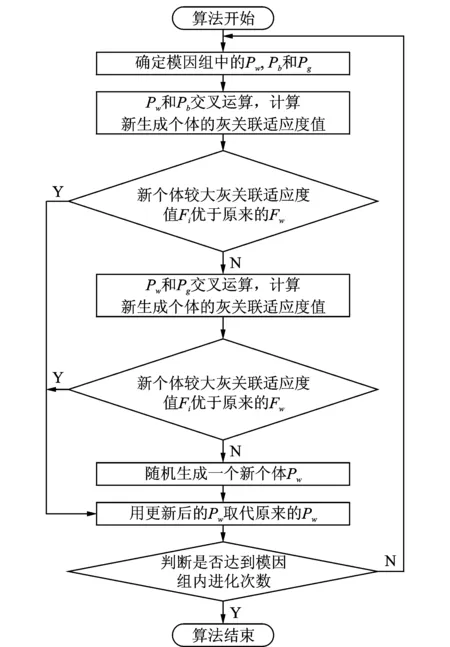
图2 局部位置更新算子流程图Fig．2 Flow chart of local position update

2.2.3 算法构成要素

在混合蛙跳算法中，分组算子和局部位置更新算子对算法的收敛速度和执行效率起关键作用，决定着算法的性能和适应性。局部位置更新算子流程如图2所示。

(1) 改进的分组算子

算法首先随机初始化一组编码序列来组成初始种群，利用灰关联综合评价法则计算所有序列的适应度值并排序，并分别放入各个模因组中。具体分组方法如下：将G个编码序列按灰关联适应度值降序排序并将其分为m个模因组，首先顺序分放前m个个体，即第1个序列进入第1个模因组，第2个序列进入第2个模因组，直到第m个序列进入第m个模因组；然后逆序分放相继的m个个体，即第m+1个序列进入第m个模因组，第m+2个序列进入第m-1个模因组，第m+m个序列进入到第1个模因组；逆序分组后再顺序分组，循环交替下去，直到所有序列分配完毕。在每个模因组中分别用Fb和Fw表示该模因组中个体的灰关联适应度最优值和最差值，对应的最优个体和最差个体分别用Pb和Pw表示，用Fg表示整个种群中的最优适应度值，对应的最优个体用Pg表示。

(2) 局部位置更新算子

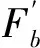
新个体移动的距离

(14)

新个体接受条件

(15)

如果新个体被舍弃，则用种群内的最优个体Pg代替组内最优个体Pb和最差个体Pw进行交叉运算，重复上述过程。如果上述方法生成的新个体仍不能代替最差的个体，则随机产生一个新个体代替原来的Pw。依照该方式，在每个模因组内部完成指定数目的进化，同时调整和更新最差个体的位置。

2.2.4 算法仿真步骤

根据算法的基本思想，算法的主要步骤如下：

(1) 初始化参数，N,M,L,W,G,m,D,Q；其中N为每个信号的码长数，M为编码相位个数，L为编码信号的个数，W为初始权向量，G为群体规模，m为模因组的数量，D为模因组内进化次数，Q为整个种群的进化次数。

(2) 随机初始化种群，产生G个个体。

(3) 计算种群内G个个体的适应度值，并降序排列后，按照改进的分组算子将G个个体分给m个模因组。

(4) 每个模因组内部执行局部位置更新算子：(1)模因组内部的最差个体与最优个体进行单点交叉运算，如果新生成个体的灰关联较大适应度值优于最差个体的灰关联适应度值，则新个体代替原来的最差个体；否则用种群内的最优个体取代模因组内的最优个体与最差个体交叉运算，若新个体的灰关联适应度值优于最差个体的灰关联适应度值，则新个体取代原来的最差个体。如果新个体都未被接受，则随机产生一个新个体。(2)重复子步骤(1)，直至达到模因组内进化次数D。

(5) 各个模因组总的所有个体进行混合，重新组成数量为G的总群体。

(6) 验证是否符合结束条件，若符合则输出最优解，否则转步骤3继续执行。

3 正交相位编码波形仿真分析

结合本文的具体优化问题，这里采用二进制编码方式，设置初始群体规模G=200，初始化权值W={2,1,2,1}，种群进化代数Q=500，模因组数量m=10，模因组内进化次数D=10。适应度函数选用目标函数的倒数表示。

表1给出了当L=4,N=40,M=4时采用混合蛙跳算法得到的一组设计结果，表中的0，1，2，3分别表示相位(0,π/2,π,3π/2)。表2给出了正交码集的归一化自相关旁瓣峰值(Autocorrelation side-lobe peak, ASP)和归一化互相关峰值(Cross-correlation peak, CP)的结果，其中，主对角线元素值为归一化ASP，非对角线元素值为归一化CP，计算可得平均ASP为0.115 3(约-18.76 dB),平均CP为0.208 9(约-13.18 dB)。

表3给出了与其他文献中所用方法的比较结果，从表中可以看出，自相关旁瓣峰值有了较明显的改善，互相关峰值也有所改善，文中所提方法可用于雷达波形设计中。但受信号总能量和码元长度的影响，若要进一步降低峰值，可以采取匹配滤波或者增加码元长度的方法。

表1 L=4,N=40,M=4时的正交码设计结果

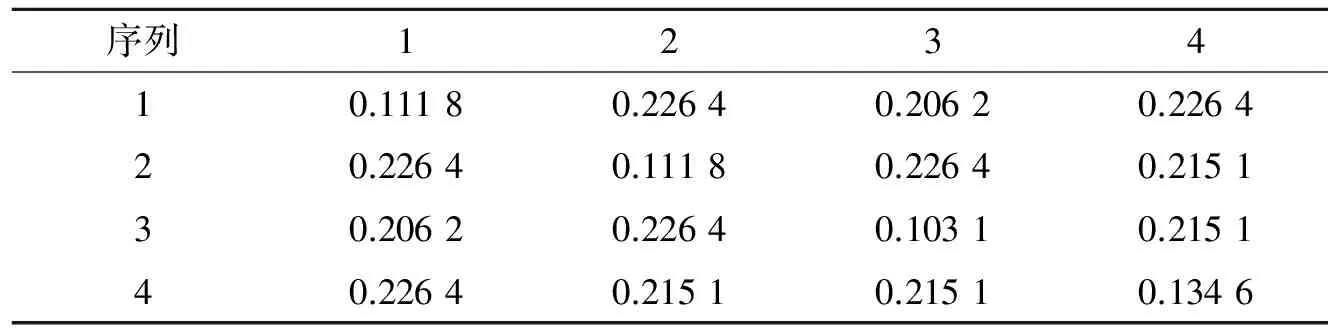
表2 L=4,N=40,M=4时正交码集的归一化ASP和CP

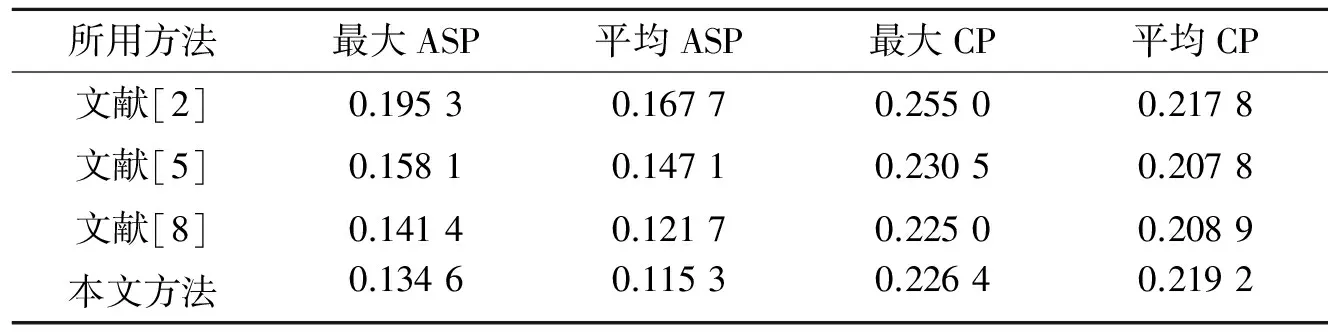
表3 本文方法与其他文献方法的比较结果

图3和图4给出了编码序列的自相关曲线和互相关曲线。由图3中可以看出，自相关旁瓣峰值有的出现于主瓣附近，有的离主瓣较远，对于目标回波只是横跨几个甚至几十个距离单元的情况而言，临近单元回波之间仍有较大干扰，可对主瓣附近区域的峰值进一步约束。

图5给出了本文改进的混合蛙跳算法与原始蛙跳算法的进化比较结果。从图中可以看出，编码序列仿真中，在所有参数都相同的情况下，改进后的算法在迭代一定次数后，适应值有明显提高，而且收敛速度加快，更容易找到最优解。

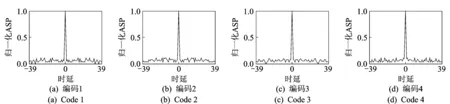
图3 序列自相关曲线Fig．3 Autocorrelation function of codes

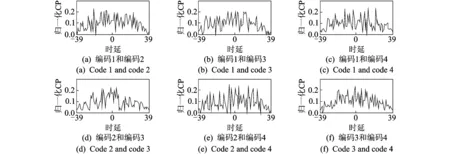
图4 序列的互相关曲线Fig．4 Cross-correlation function of codes

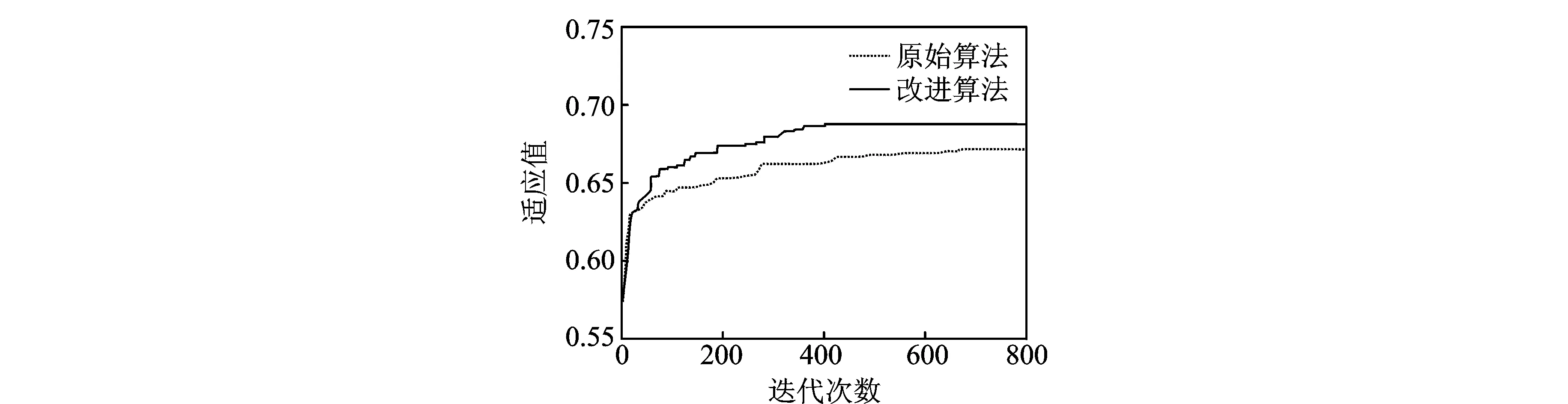
图5 两种不同算法的进化结果Fig．5 Evolution results of two different algorithms

4 结束语

本文提出了一种可用于雷达波形设计的灰关联混合蛙跳算法。该算法以原始蛙跳算法为基础，在分组进化时与遗传算法相结合，同时对原始蛙跳算法的分组方法加以改进，丰富了种群的多样性，同时引入灰关联综合评价比较个体的适应度。仿真结果表明，该算法采用模因分组方法分为不同的子群体进行搜索，不易陷入局部极小值，寻优能力更强，具有较快的收敛速度和较强的鲁棒性，可以设计出有效的雷达正交编码波形，为自相关和互相关受限的雷达波形设计提供了有利工具。

[1] Deng H．Synthesis of binary sequences with good autocorrelation and cross-correlation properties by simulated annealing[J]．IEEE Transactions on Aerospace and Electronic Systems，1996，32(1)：98-107．

[2] Deng H．Polyphase sequences design for orthogonal netted radar systems[J]．IEEE Transactions on Signal Processing，2004，52(11)：3126-3135．

[3] 陶海红，廖桂生，王伶．基于混合遗传算法的m序列波形优化设计[J]．电波科学学报， 2004，19(3)：253-257．

Tao Haihong，Liao Guisheng，Wang Ling．Novel m-sequences waveform design using the hybrid genetic algorithm[J]．Chinese Journal of Radio Science， 2004，19(3)：253-257．

[4] Singh S P， Rao K S．Discrete frequency-coded radar signal design[J]．IET Signal Processing，2009，3(1)：7-16．

[5] 刘波，何子述．基于遗传算法的正交多相码设计[J]．电子测量与仪器学报，2006，22(2)：62-66．

Liu Bo，He Zishu．Genetic algorithm based MIMO radar polyphase code design[J]．Journal of Electronic Measurement and Instrument，2006，22(2)：62-66．

[6] Liu B．Orthogonal discrete frequency-coding waveform set design with minimized autocorrelation side-lobes[J]. IEEE Trans on Aerospace and Electronic Systems，2009，45 (4)：1650-1657．

[7] 刘波，何子述，王海江．MIMO雷达中的DFCW设计及性能分析[J]．电子科技大学学报，2010，39(5)： 688-691.

Liu Bo，He Zishu，Wang Haijiang．DFCW signal design and performance analysis for MIMO radar[J]． Journal of University of Electronic Science and Technology of China， 2010，39(5)： 688-691．

[8] Gong Shufeng，Long Weijun，Huang Hao，et al． Polyphase orthogonal sequences design for opportunistic array radar via HGA[J]．Journal of Systems Engineering and Electronics，2013，24(1)：60-67．

[9] 曾祥能，张永顺，田波，等．基于Grefenstette编码下MicPSO的离散频率编码波形设计[J] ．电子与信息学报，2011，33(1)：100-105．

Zeng Xiangneng， Zhang Yongshun，Tian Bo， et al．Discrete frequency code waveform based on MicPSO cooperated with Grefenstette coded[J]． Journal of Electronics & Information Technology， 2011，33(1)：100-105．

[10]施群，张弓，刘文波．混沌理论在MIMO雷达波形设计中的应用[J]．数据采集与处理，2010，25(4)： 525-529．

Shi Qun，Zhang Gong，Liu Wenbo．Application of chaos theory to MIMO radar waveform design[J]．Journal of Data Acquisition and Processing，2010，25(4)：525-529．

[11]Eusuff M M，Lansey K E．Water distribution network design using the Shuffled Frog leaping algorithm[C]∥ Proceedings of the 1st IWA World Water Congress.Paris，France：Intl Water Assn Press，2001．

[12]罗雪晖，杨烨，李霞.改进混和蛙跳算法求解旅行商问题[J].通信学报，2009，30(7)：130-135．

Luo Xuehui，Yang Ye，Li Xia．Modified shuffled frog-leaping algorithm to solve traveling salesman problem[J]．Journal on Communications，2009，30(7)：130-135．

[13]Eusuff M M，Lansey K E．Optimization of water distribution network design using the shuffled frog leaping algorithm[J]．Water Resource Plan Manage，2003，129(3)：210-225．

[14]Elbeltagi E，Hegazy T，Grierson D． Comparison among five evolutionary-based optimization algorithms[J]．Advanced Engineering Informatics，2005，19(1)：43-53．

[15]Elbeltagi E，Hegazy T，Grierson D．A modified shuffled frog-leaping optimization algorithm: Applications to project management[J]． Structure and Infrastructure Engineering，2007，3(1)：53-60．

[16]Zhen Z Y，Wang Z S，Gu Z，et al．A novel memetic algorithm for global optimization based on PSO and SFLA[J]．Lecture Notes in Computer Science，2007，4386：127-136．

[17]Zhang X C，Hu X M，Cui G Z，et al．An improved shuffled frog leaping algorithm with cognitive behavior[C]∥Proceedings of the 7th World Congress on Intelligent Controland Automation.Chongqing，China：IEEE Conference Publications，2008：6197-6202．

[18]李英海，周建中，杨俊杰，等.一种基于阀值选择策略的改进的混合蛙跳算法[J]．计算机工程与应用，2007，43(35)：19-21．

Li Yinghai，Zhou Jianzhong，Yang Junjie，et al．A modified shuffled frog leaping algorithm based on threshold selection strategy[J]． Computer Engineering and Applications，2007，43(35)：19-21．

[19]邓聚龙．灰色系统基本方法[M]．武汉:华中科技大学出版社，2005：74-106．

Deng Julong．The primary methods of grey system theory[M].Wuhan：Huazhong University of Science and Technology Press，2005：74-106．

[20]Tsai M S，Hsu F Y．Application of grey correlation analysis in evolutionary programming for distribution system feeder reconfiguration[J]．IEEE Transactions on Power Systems，2010，25(2)：1126-1133．

[21]柯红发，陈永光，夏斌．一种基于逼近于理想灰关联投影的多目标决策算法[J]．电子学报，2007， 35(9)：1757-1761．

Ke Hongfa，Chen Yongguang， Xia Bin．An algorithm of multiple criteria decision-making based on similarity to ideal grey relational projection [J]．Acta Electronica Sinica，2007，35(9)：1757-1761．

Waveform Design for Radar Based on Shuffle Frog Leaping Algorithm with Grey Correlation Evaluation

Long Weijun1,2, Gong Shufeng1, Han Qinghua1, Shang Ni1, Ben De1,2

(1. Key Laboratory of Radar Imaging and Microwave Photonics of Ministry of Education, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China； 2. Nanjing Research Institute of Electronics Technology, Nanjing, 210039, China)

Shuffle frog leaping algorithm(SLFA) combined with the grey correlation evaluation is proposed for designing orthogonal waveform. SLFA plays the dominant role in the new algorithm. Meanwile genetic operators of genetic algorithms(GAs) are introduced in the local position update and the group dividing method of SFLA is modified to improve the diversity of population. Moreover, the fitness function is evaluated with the grey correlation model. Polyphase orthogonal waveforms with low autocorrelation and cross-correlation are taken as an example in the radar waveform design. Simulation results verify that the waveform generated by using the proposed algorithm obtains better orthogonal performance, thus the algorithm is effective for designing radar orthogonal signals.

shuffle frog leaping algorithm； genetic operators； grouping method； grey correlation evaluation；orthogonal waveform

国家自然科学基金(61071164，61271327)资助项目；中国博士后基金(2015M580426)资助项目；江苏省高校优势学科建设工程资助项目；江苏省博士后基金(1501056B)资助项目。

2015-10-12；

2015-11-05

TN911.7