基于优化相关向量机的财政支出项目绩效评价

王继龙

(华北电力大学经济与管理学院，北京 102206)

0 引言

作为财政、预算部门判断财政支出产出和效果的重要工作内容，财政支出项目绩效评价可以有效地提高财政资金的使用效益。公共投资项目绩效评价起源于1993 年美国颁布的《政府绩效与结果法案》(The Government Performance and Results Act of 1993)，该法标志着美国财政支出项目绩效评价工作正式开始，并逐步在西方发达世界得到广泛应用。2011 年，我国财政部印发《财政支出绩效评价管理暂行办法》 (财预〔2011〕285号)，标志着我国财政支出项目绩效评价工作步入全面发展阶段。

目前，我国主要行业、主要省区市基本完成财政支出项目绩效评价指标体系的建立［1-4］，并在近几年的财政支出项目绩效评价工作中逐步展开试点、推广应用工作。在实际财政支出项目绩效评价工作中，由于主管部门需要评价的项目较多，在评价时需要投入专家成本较高、耗费时间较长，尚未做到经济有效地对全部项目的绩效评价，而是采用对一部分项目进行评价、以该部分项目评价结果代表所有项目评价结果，这样就导致了评价的不全面性、不公平性，并为人为规避某些财政支出项目绩效评价创造了可能。

本文提出一种基于优化相关向量机(Relevance Vector Machine，RVM)［5］的财政支出项目绩效评价方法。RVM 是在支持向量机 (Support Vector Machine，SVM)基础上发展起来的一种新的机器学习方法，在负荷和功率预测［6-7］、缺陷检测［8-9］、图像识别［10-11］等领域展开了应用研究并取得了一定成果。本文在现有评价方法基础上，以完成专家评价的项目作为RVM 训练样本，充分利用RVM 预测精度高、泛化能力强、较小样本空间即可满足训练要求等优点，在对样本项目应用RVM 进行训练、学习之后对全部项目进行评价，避免了现有项目绩效评价方法专家成本高、评价时间长等不足，实现了全部项目的无偏差绩效评价，评价过程更为客观和公正，尤其适用于财政支出项目绩效评价主管部门需要对大批项目进行评价的情况。

1 建模理论

1.1 RVM 回归预测

RVM 主要理论基础包括贝叶斯理论、马尔科夫性质、自相关判断理论 (Automatic Relevance Determinatiaon，ARD)和最大似然等。与人工神经网络 (Artificial Neural Networks，ANN)等智能预测方法相比，RVM 方法具有更强的非线性映射能力，对样本数据的依赖性相对较小，具有更强的泛化能力。与SVM 相比，RVM 具有更好的稀疏性，极大地减少了核函数的计算量，核函数可以任意使用且不用满足Mercer 条件。

RVM 假设权值参数ω 是受超参数α 控制的高斯(Gaussian)先验概率分布，在贝叶斯框架下通过机器学习，并利用ARD 对不相关的点进行删减以获得稀疏化模型。非零权值的基函数所对应的样本向量称为“相关向量”，体现了数据中最核心的特征。

RVM 回归预测模型可以描述为［5］

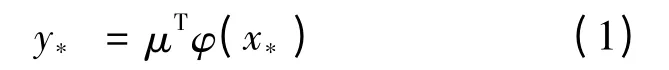
式中，φ(x)=(φ1(x)，φ2(x)，…，φN(x))T(N 为样本数)为基函数;μ 为均值向量;y*为预测均值。

由式(1)可知，新样本x*的预测值均值为y(x*，μ)。若给定新的输入值x，则其相应的输出概率分布服从Gaussian 分布，相应的预测值为y*。

1.2 GA

GA 等参数优化方法常用来根据具体问题优化具体参数，以确定预测模型参数最优［12-13］。GA 是一种基于自然选择和遗传规律的启发式、并行的全局搜索最优方法，其主要源自于自然界的选择和进化理论，常用来解决目标函数的多参数优化问题。GA 通常包含参数初始化、选择、交叉和变异等步骤。应用GA 解决现实问题时，最重要的是选择好适应度函数。

1.3 PCA

主成分分析 (Principal Component Analysis，PCA)常用来对高维数据进行降维处理，以有效降低数据维度，提取数据的主成分，从而简化计算过程，提高计算速度。PCA 的基本思想是将具有一定相关性的原始数据，通过线性组合变换成一组新的、维度更低的几个相互独立或互相无关的变量来代替原始数据。PCA 主要通过对原始数据的协方差矩阵进行特征分解，求出主成分以及对应权值。

2 GA_RVM 模型

2.1 建模流程

基于遗传优化相关向量机的财政支出项目绩效评价模型(以下简称“GA_RVM 模型”)保留现有财政支出项目绩效评价方法中的专家评价部分，应用该部分项目的专家评价结果作为RVM 训练样本，通过RVM 训练、优化，学习后输出最佳RVM 预测模型，应用该RVM 最佳预测模型对其他样本 (测试项目)进行测试，即可得到全部项目的综合评价结果。同时考虑到专家评价样本项目集较小，对评价指标体系进行主成分分析降维处理、在RVM 训练和优化时采用K-折 (K-fold)交叉验证，以提高训练的有效性和模型的拟合性。GA_RVM 模型建模流程见图1。

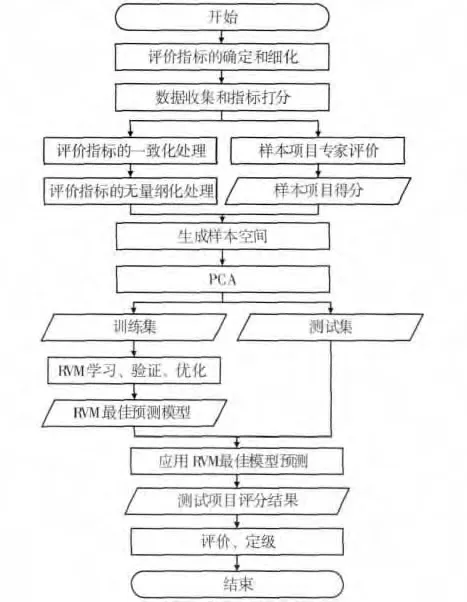
图1 GA_RVM 模型建模流程

2.2 评价指标的确定、细化和打分

绩效评价工作小组接受评价委托任务后，首先需要根据评价任务和评价项目特点，确定需要采用的绩效评价指标体系。在评价指标体系中，三级指标是细化的、可执行的具体指标，绩效评价工作小组根据确定的评价指标体系及三级指标开展具体的评价工作。绩效评价指标体系的三级指标见表1。

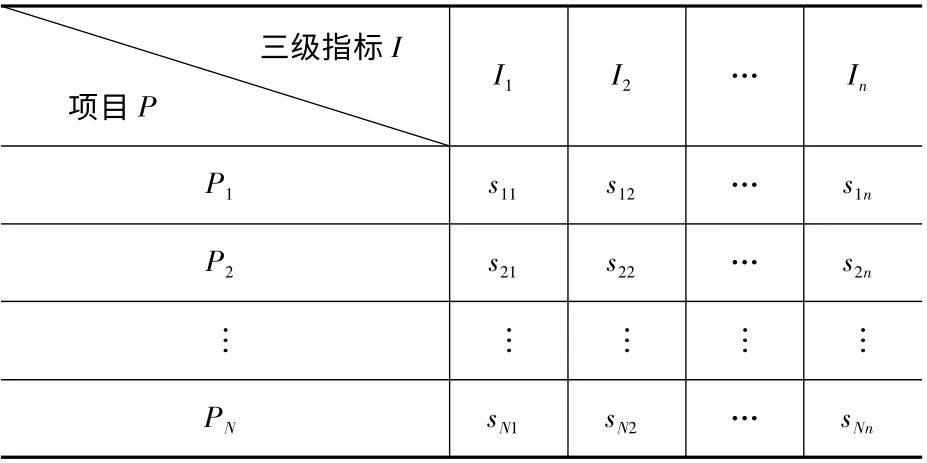
表1 评价指标体系三级指标

绩效评价工作小组根据三级指标及相应的评分标准对各项目基础数据、现场资料等进行收集和审核，并对其进行打分，组成各项目最原始的基础数据信息。

2.3 指标得分数据预处理

在财政支出项目绩效评价的三级指标体系中，评价指标通常包括极大型指标、极小型指标、中间型指标和区间型指标。GA_RVM 模型将上述指标统一转化为极大型指标。

在进行财政支出项目绩效评价过程中，各指标由于各自量纲和量级的不同而存在着不可公度性，为综合评价的比较带来不便。因此，为了消除各指标量量纲不同及其数值数量级间的差别所带来的影响，需要对指标做无量纲化处理。指标的无量纲化，也称指标的标准化，通过数学变换的方式来消除原始指标量纲的影响。

常用的线性化处理方法有标准化处理法、线性比例处理法以及归一化处理法。在实际研究应用中，根据不同的研究目标选用不同的方法。GA_RVM 模型采用线性比例法进行指标的无量纲化处理，数学表达式为

评价指标的无量纲化处理通过数学变换来消除不同指标之间由于量纲的不同带来的不利影响，以更真实地反映实际情况，排除由于不同指标、不同量纲，以及不同数值数量级之间的差异性带来的不利影响，避免不合理现象，提高财政支出项目绩效评价的可行性和合理性。

2.4 样本项目专家评价和生成样本空间

绩效评价专家小组针对样本项目，根据绩效评价工作小组提供的样本项目基础数据，现场资料等，以及根据专家评审会上项目单位的现场答辩情况，各专家对项目的综合了解情况，并对样本项目绩效评价情况进行综合打分，得到每个样本项目的评价得分。

样本项目的绩效评价工作小组评价打分结果、专家评价得分结果一一对应即组成RVM 的训练样本空间。绩效评价专家小组评价得分结果与绩效评价工作小组评价打分结果函数关系式如下

式中，S = ［S1，S2，…，SN］ 表示各项目绩效评价专家小组的评价得分;I= ［I1，I2，…，IN］表示每一个项目细化评价指标的绩效评价工作小组评价打分;e = ［e1，e2，…，eN］表示各项目训练、测试过程中的误差;N 为项目数;n 为细化的评价指标数。

其他项目的绩效评价工作小组评价打分结果即组成RVM 测试样本空间的输入部分，其输出需要应用学习后的RVM 模型进行测试后得出。样本空间划分及指标得分、综合评价得分见表2。

考虑到完成专家评价的样本项目一般来说容量较小，且三级评价指标一般来说在十几个左右，为有效提高模型学习和泛化能力，应用PCA对绩效评价工作小组评价打分结果进行降维处理。

?

2.5 RVM 训练、优化和预测

RVM 对训练样本空间进行学习，以绩效评价工作小组评价打分结果作为模型输入、绩效评价专家小组评价得分作为输出进行模型的学习。考虑到样本空间较少，GA_RVM 模型应用K-fold交叉验证。经过RVM 训练，输出最佳RVM 预测模型。

2.5.1 RVM 核函数的选择

RVM 核函数的选择由于不受Mercer 条件的约束，所以理论上可以使用任何核函数。在理论研究和实际应用中，经常选用径向基 (Radial Basis Function，RBF)核函数、线性核函数和多项式核函数等。RBF 拟合性强，具有较强的学习能力，适用于高、低维以及大、小样本等多种情况。在理论研究和实际应用中，RBF 常被选为RVM 的核函数，其数学表达式如下

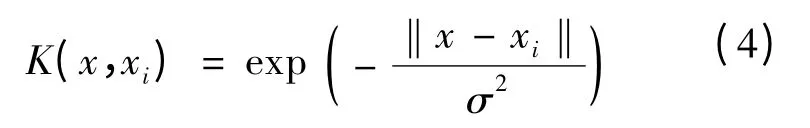
式中，x 为输入向量;x1为训练集中第i 维输入向量;σ2为核函数的宽度。

2.5.2 RBF 核参数的GA 优化

RBF 核参数的σ2值对预测结果有较大的影响，本文应用GA 算法获取最佳预测模型中RBF核参数σ2的最优值。

GA_ RVM 模型选用绝对平均百分比误差(Mean Absolute Percentage Error，MAPE)作为评价标准，记为IMAPE，其计算公式如下

RVM 根据训练样本空间K-fold 交叉验证划分的验证集IMAPE进行GA 优化。利用优化得到的最佳RVM 模型对测试样本进行测试。将测试样本的绩效评价工作小组打分结果输入最佳RVM模型，即可得到测试样本的测试得分，从而完成其他项目的评价，输出测试得分。

RVM 通过对训练样本空间，即样本项目的学习，识别出相应变化规律，并通过K-fold 交叉验证避免了样本项目较少的不足，保证了预测模型的最佳，确保了各项目测试得分的准确性。

2.6 全部项目的评价定级

财政支出项目绩效评价绩效级别分为四级，项目评价合计得分90 分(含)以上的为优秀，75 (含) ～90 分的为良好，60 (含) ～75 分的为一般，60 分以下的为较差。这样，就可以根据各项目绩效评价得分落入的评价区间，判断财政资金投入的效益和效果。

3 案例分析

本文以某年度某部门主管的30 个项目为例进行财政支出项目绩效评价分析。其评价指标体系见表3。

表3 财政支出项目绩效三级评价指标体系

PCA 各成分累计贡献率阀值取为0.98。

GA 种群规模100，终止代数20，交叉率0.8，变异率0.05，适应度函数为IMAPE。

为便于进行RVM 测试项目测试得分的对比，组织7 位专家(技术、经济专家各2 人，业务专家3 人)对全部项目进行评价。同时，选取15个项目作为样本项目，进行RVM 训练、优化，输出最佳RVM 预测模型，应用最佳RVM 预测模型对其他15 个项目进行了测试。

RVM 训 练IMAPE为0.66%，测 试IMAPE为3.02%，其训练结果、测试结果见图2。由图2可知，GA_RVM 模型训练、测试结果良好，专家评价得分和 RVM 测试得分基本吻合，GA_RVM模型以较少的训练样本 (15 个项目)实现了对全部项目评价规律的识别，测试准确度良好。但可以看出，测试项目测试得分和专家评价得分有一定出入，导致RVM 测试绩效级别和专家评价绩效级别存在一定出入，并且存在个别项目的绩效级别不一致(如:绩效级别边界点的测试项目2)，但总体上应用GA_RVM 模型展开财政支出项目绩效评价具有较高的准确性。

图2 GA_RVM 模型训练、测试结果图

4 结语

本文提出一种基于优化相关向量机的财政支出项目绩效评价方法，与现有财政支出项目绩效评价方法相比:

(1)GA_RVM 模型在几乎不增加专家评价成本的基础上实现所有项目的绩效评价，且评价准确性与专家评价结果基本吻合，可以减少大量人力、财力，产生较为显著的经济效益，并提高评价效率。

(2)将现有评价方法中的专家资源集中投放在样本项目的评价中，可以提高评价的准确性、公平性和客观性。

(3)GA_RVM 模型特别适用于同类项目较多时的财政支出项目绩效评价。

［1］ 胡景男. 北京地区高等教育财政支出绩效评价研究［D］.北京:北京化工大学，2011.

［2］ 郑海宁. 成本-效益分析法在农业财政支出绩效评价中的应用研究［D］. 保定:河北农业大学，2013.

［3］ 梁宏亮，黄欣涔. 基于AHP 模型的灾害救援重建财政支出绩效评价研究［J］ . 当代教育理论与实践，2012 (8):171-174.

［4］ 周普. 水利财政支出绩效评价分析［J］. 中国水利水电科学研究院学报，2012，10 (1):73-76，80.

［5］ Tipping M E. Sparse Bayesian learning and the relevance vector machine ［J］ . The Journal of Machine Learning Research，2001 (1):211-244.

［6］ 段青，赵建国，马艳. 优化组合核函数相关向量机电力负荷预测模型［J］. 电机与控制学报，2010，14 (6):33-38.

［7］ BAO Yan，WANG Hui，WANG Beining. Short-term wind power prediction using differential EMD and relevance vector machine［J］. Neural Computing and Applications，2014，25 (2):283-289.

［8］ ZHU Fengyu，WANG Qi，SHEN Zhengguang. APSO-RVM for fault detection of liquid rocket engines test-bed ［J］. Information Technology Journal，2012，11 (10):1496-1501.

［9］ Tran V T，Yang B S，Gu F，et al. Thermal image enhancement using bi-dimensional empirical mode decomposition in combination with relevance vector machine for rotating machinery fault diagnosis ［J］. Mechanical Systems and Signal Processing，2013，38 (2):601-614.

［10］ 赵春晖，齐滨，张燚. 基于改进型相关向量机的高光谱图像分类［J］. 光学学报，2012，32 (8):264-269.

［11］ 张昱，谢小鹏. 基于遗传相关向量机的图像分类技术［J］. 计算机仿真，2011，28 (5):283-286.

［12］ Barszcz T，Bielecka M，Bielecki A，et al.Wind speed modelling using Weierstrass function fitted by a genetic algorithm ［J］.Journal of Wind Engineering and Industrial Aerodynamics，2012，109 (6):68-78.

［13］ Liu Da，Niu Dongxiao，Wang Hui，et al. Short-term wind speed forecasting using wavelet transform and support vector machines optimized by genetic algorithm ［J］ . Renewable Energy，2014，62 (2):592-597.