多通道测力仪动态信号反向滤波补偿方法

朱明,毛宽民

(华中科技大学机械科学与工程学院,430074,武汉)



多通道测力仪动态信号反向滤波补偿方法

朱明,毛宽民

(华中科技大学机械科学与工程学院,430074,武汉)

为了消除动态测力仪的结构动态特性对测试结果的干扰,采用反向滤波的方法对动态力测试信号进行修正。根据最小相位系统理论设计反向数字滤波器,由单输入单输出反向数字滤波器的设计原理,提出了多输入多输出反向数字滤波器的设计方法。根据测力系统激励力与测试值之间的频响函数矩阵,建立测力系统传递函数模型,并进行最小相位转化,将最小相位动态力传递函数模型反转,得到反向滤波器。实验结果表明:经过反向滤波处理的动态力测试值与实际动态力具有相同的幅值;运用零相位滤波方法,消除了测试信号与实际动态力之间的相位差;测试结果与动态力实际输入幅值误差小于6%。

动态测力仪;反向滤波;最小相位;频响函数;零相位滤波

准确测量动态切削力对切削过程的建模研究以及验证研究均具有重要作用[1-2]。在动态切削力测试过程中,通常将刀具或者工件安装在测力仪之上,测试结果可以用于动态力系数的标定以及切削过程稳定性建模研究[3]。但是,动态力测试结果受到测力仪本身及其附加结构的动态特性的影响[4]。一般情况下,切削点距离测力仪中心的位置越远,动态力测试精度越低,并且各个方向测试结果的交叉影响也越严重[5-6]。

为了准确测试动态力,现有研究主要包含测力仪结构优化和信号补偿两类办法。测力仪结构优化方法主要是开发小型化测力仪,并将其安装在靠近切削点附近[5-7]。信号补偿方法主要是根据测力系统的动态特性来滤除实测信号中的干扰项。文献[8]将测力仪附加结构的质量视为动态力测试的干扰源,通过在动态力测试结果中去除附加质量惯性力的方法来提高测试精度。这种基于附加质量惯性力的方法被广泛应用于动态力测试研究中。文献[9]提出一种基于传递函数的反向滤波器设计方法,对动态力进行了补偿。以上动态力测试补偿方法建立在动态力交叉传递特性可忽略的基础之上,通常不适用于实际测试条件。有研究者提出了一些新的补偿方法[1,10-11],如设计卡尔曼滤波器对测试信号进行修正,但是往往需要复杂的实验测试和数据处理工作。

本文运用反向滤波的方法,对动态力测试信号进行修正,分析了实际测试系统中各个方向动态力之间的相互影响,将反向滤波补偿方法进行拓展,应用于多通道动态力测试过程中。

1 反向滤波补偿原理

在使用测力仪测量动态切削力时,需要将刀具或者工件安装在测力仪之上。由于测力仪附加结构的影响,测力仪输出切削力fm与实际切削力f之间存在一定的差异。在Z域内,定义测力仪输入与输出之间的传递函数如下

H(z)=Fm(z)/F(z)

(1)

在理想状态下,动态力不受测力系统结构动态特性的影响,动态力传递函数H(ω)在任何频率处均等于1。但是,测力仪附加结构的惯性质量以及动态变形均会引起动态力测试结果的失真,如图1所示。

图1 动态力测试结果失真原理

如果已知动态力传递函数H(z),则可以利用反向滤波原理设计滤波器H-1(z),将动态力测试信号fm进行反向滤波,即得到真实的动态力f。

如果H(z)代表一个稳定的最小相位系统,即其z变换的零点和极点均在单位圆以内,则该系统是可逆的。将式(1)经过分子分母的反转得到的滤波器H-1(z),可以直接用于动态力测试结果的补偿上。但是,实际的测力系统往往是稳定非最小相位系统,即在z平面内,测力系统的极点在单位圆以内,但是零点不全在单位圆以内。H-1(z)所代表的系统的极点不全在单位圆以内,因此是不稳定的。如果直接将滤波器H-1(z)用于动态力测试结果的补偿,则输出的结果将趋向于无穷大。

如果将H(z)所代表的系统转换成最小相位系统,相应的最小相位传递函数Hmin(z)与H(z)具有相同幅值,仅相位发生改变。根据最小相位传递函数Hmin(z)经反转得到的滤波器是稳定的,可以用于动态力测试结果的修正。

2 最小相位传递函数

对于一个单输入、单输出(SISO)非小相位系统,假设其单位脉冲响应序列为h(n),则可以通过拟合方法得到传递函数为H(z)。该系统可以表示为一个最小相位系统Hmin(z)和全通系统Hap(z)的级联,即在Z域内可以表示为

H(z)=Hmin(z)Hap(z)

(2)

假设系统H(z)有n个零点1/z0(z0<1)处于单位圆以外,其余零点和极点均在单位圆以内。将单位圆外的零点的因式分解出来,得到

H(z)=H1(z)(z-1-z0)

(3)

其中H1(z)的零点和极点均在单位圆以内,所以H1(z)是一个最小相位系统的传递函数,但是(z-1-z0)并不是一个全通系统。为了将H(z)分解为最小相位系统和全通系统的级联,可以将式(3)作如下变形

Hmin(z)Hap(z)

(4)

3 多输入、多输出反向滤波器设计方法

在多输入、多输出(MIMO)的动态力系统中,各个通道之间会产生相互影响。比如,x方向的动态力会使测力仪在y方向上产生非零输出,各个方向上动态力之间的相互影响使得动态力测试结果失真。以两个方向动态力之间的相互干扰为例,假设x和y方向上动态力与测试值之间的关系表示为

Fm(z)=H(z)·F(z)

(5)

假设矩阵H(z)是满秩的。事实上矩阵H(z)是通过对实测频响进行拟合得到,总可以得到满秩矩阵。与前述SISO传递函数类似,可以设计一个反向滤波系统H-1(z)用于修正动态力测试结果Fm(z)。

对于矩阵H(z),假设其所有元素的有理分式的最小公分母为d(z),则

(6)

式中:N(z)是一个多项式矩阵。

根据式(6),得

(7)

式中:N*(z)为N(z)的伴随矩阵。根据式(6)可知N(z)中各元素为多项式,所以N*(z)中各元素为多项式。

根据式(7)可知,H-1(z)的极点即为多项式|N(z)|的零点。与SISO反向滤波器设计原理相同,为了设计稳定的MIMO反向滤波器,需要将动态力传递函数矩阵H-1(z)进行转换。将多项式|N(z)|的零点全部转换到Z域单位圆以内,得到最小相位多项式|Nmin(z)|。

根据式(7),可得到用于动态力测试结果补偿的反向滤波器

(8)

将动态力信号经反向滤波器滤波和相位补偿之后可以得到真实的动态力信号。

4 实验测试

在图2所示的切削系统中,利用自行设计的夹具将测力仪安装在刀塔转盘上,并将刀具安装在测力仪上。切削过程中的振动会引起测力系统结构(图2b)的动态变形,造成各个方向动态力之间的相互干扰。利用反向滤波的方法可以对动态力测试结果进行修正。

(a)测试机床

(b)测力系统示意图图2 实验测试平台

4.1 反向滤波器设计

使用锤击法测试刀尖激励力F(ω)与测力仪输出信号Fm(ω)之间的频响函数H(ω),如图3所示。在1 539、1 867和2 190 Hz等频率处,由于测力系统结构动态特性的影响,动态力测试结果受到明显的干扰,并且x和y方向动态力信号也产生了相互干扰。

利用MATLAB®信号处理工具箱识别动态力传递函数矩阵H(z)。根据实际拟合精度的需要,利用ARMA(2n,2n-1)滑动平均建模方法确定传递函数阶数[12]。由传递函数矩阵计算得到频响函数矩阵H(ω)拟合值,图3显示了测试及拟合传递函数矩阵H(ω)的各个元素。

(a)x方向直接频响Hxx(ω)

(b)xy方向交叉频响Hxy(ω)

(c)yx方向交叉频响Hyx(ω)

(d)y方向直接频响Hyy(ω)图3 测力系统频响函数测试值及拟合值

按照式(6)～式(8)所述方法,计算得到测力系统反向滤波器传递函数矩阵HC(z),将其转换为频响函数矩阵HC(ω),图4所示为矩阵HC(ω)中的各个元素。

为了研究反向滤波器设计方法的有效性,对测力系统x和y方向施加脉冲激励fx(t)和fy(t),两个方向脉冲的施加时刻不同,如图5a、图5b所示。从图5c、图5d可以看出,测力系统输出信号fxm(t)和fym(t)因受到系统结构动态特性的影响而失真,并且两个方向输出信号之间相互干扰。运用反向滤波器HC(z)对测力系统输出信号fxm(t)和fym(t)进行滤波。图5e、图5f所示为滤波后得到的信号fxa(t)和fya(t)。可以看出,经过滤波得到的信号与测力系统输入信号的幅值相等。

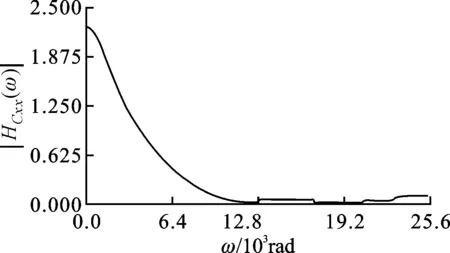
(a)x方向直接频响HCxx(ω)

(b)xy方向交叉频响HCxy(ω);

(c)yx方向交叉频响HCyx(ω)

(d)y方向直接频响HCyy(ω)图4 反向滤波器频响函数

将补偿后的信号fxa(t)(或者fya(t))与系统输入信号fx(t)(或者fy(t))在频域内进行比较,可以得到输出值与输入值之间的幅值和相位关系,见图6。反向滤波后所得信号与真实输入信号的幅值相同,但是存在相位差。相位差来源于测力系统传递特性和反向滤波器的相位损失。

为了反映真实信号的相位信息,根据零相位滤波法对测试信号及其滤波过程进行修正[13]。零相位滤波过程可以通过MATLAB®软件中filtfilt函数实现。将测试信号fxm(t)(或者fym(t))的反向序列输入动态力测试系统H(z);再将输出信号的反向序列输入到反向滤波器,进行零相位滤波后得到最终的动态力测量值fxr(t)(或者fyr(t)),如图5g、图5h所示。

从图6可以看出,经过反向滤波和相位修正,测试信号可以反映动态力测试系统的真实输入值。

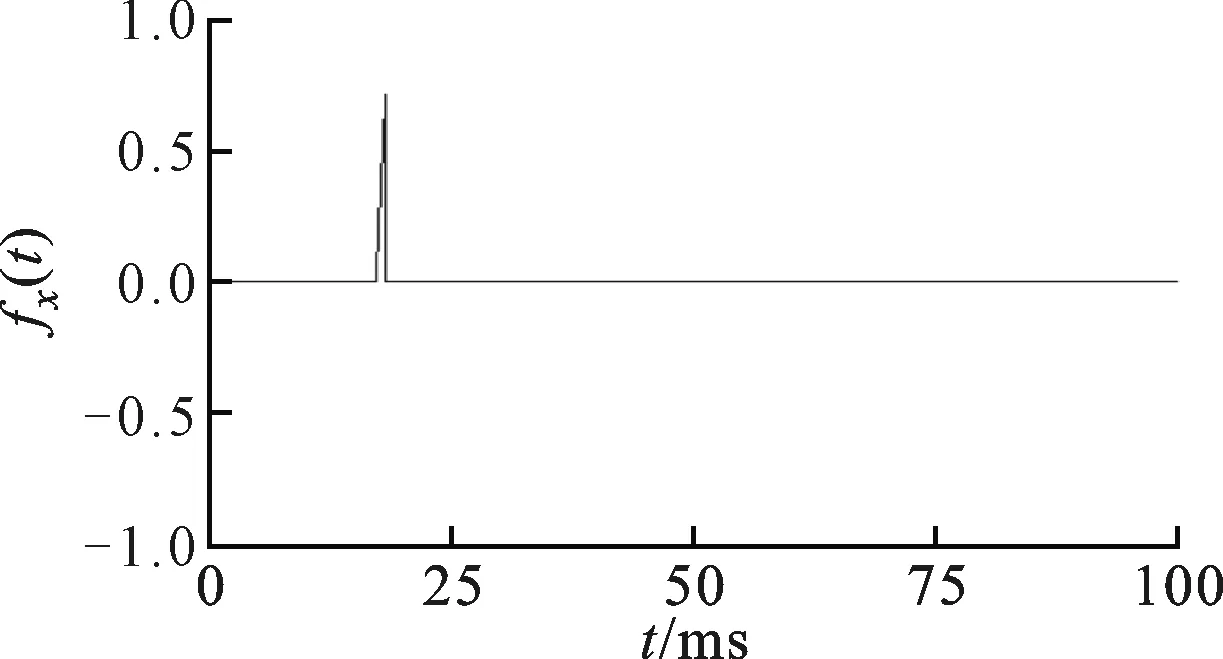
(a)x通道脉冲激励

(b)y通道脉冲激励

(c)x通道响应序列

(d)y通道响应序列

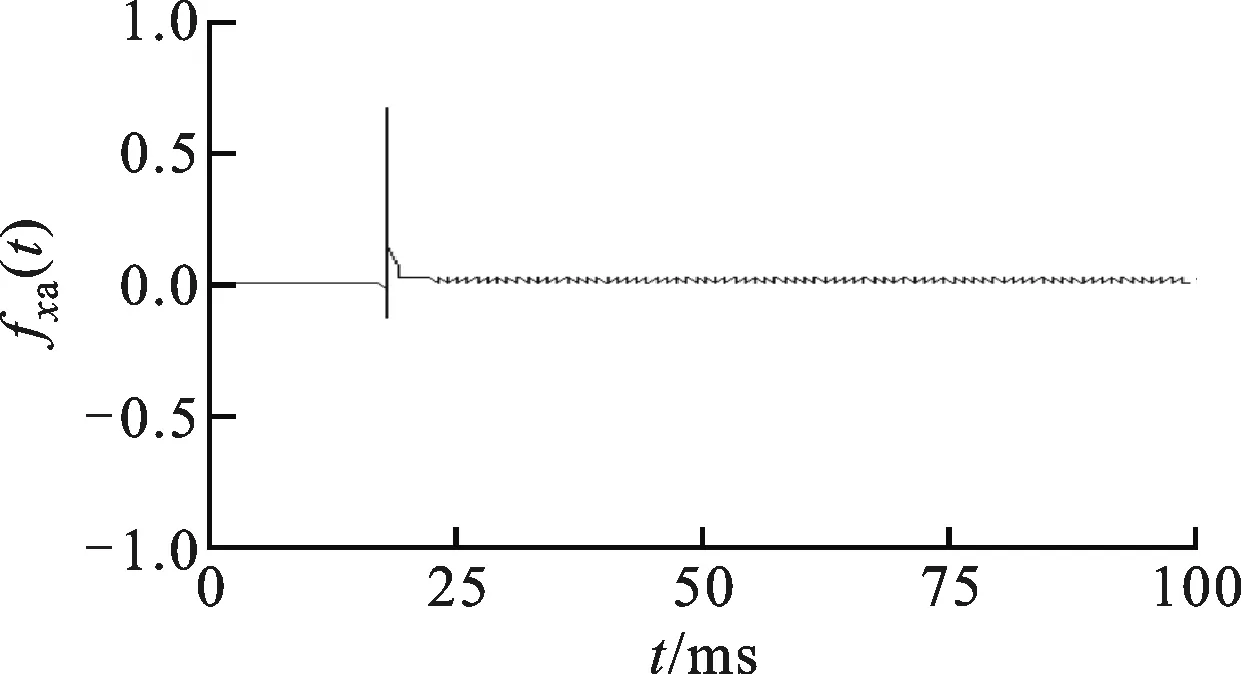
(e)x通道反向滤波后信号

(f)y通道反向滤波后信号

(g)x通道反向滤波和相位补偿后信号

(h)y通道反向滤波和相位补偿后信号图5 测力系统动态响应及滤波补偿

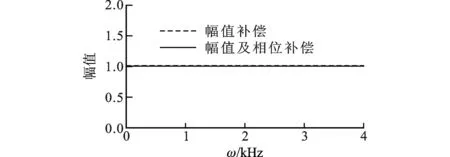
(a)x通道幅值谱

(b)y通道幅值谱

(c)x通道相位谱

(d)y通道相位谱图6 滤波后输出信号与输入信号频响函数

4.2 动态力测试

沿着x方向使用力锤敲击刀尖,同时记录力锤激励力fx(t)和测力仪输出信号fxm(t)和fym(t),如图7a、图7d所示。其中,由于没有在y方向进行激励,所以将y方向激励信号设置为0。图7c、图9d表明,测力仪输出信号与实际激励信号不符。使用前面设计的反向滤波器HC(z),对测力仪输出信号fxm(t)和fym(t)进行反向滤波和相位修正,可以得到最终的动态力测试结果fxr(t)和fyr(t),如图7所示。由于测力系统传递函数H(z)的识别存在误差,使得最终测试结果(图7g)与实际输入值(图7a)存在误差,其中峰值误差均小于6%。

(a)x通道激励信号

(b)y通道激励信号

(d)y通道响应序列

(e)x通道反向滤波后信号

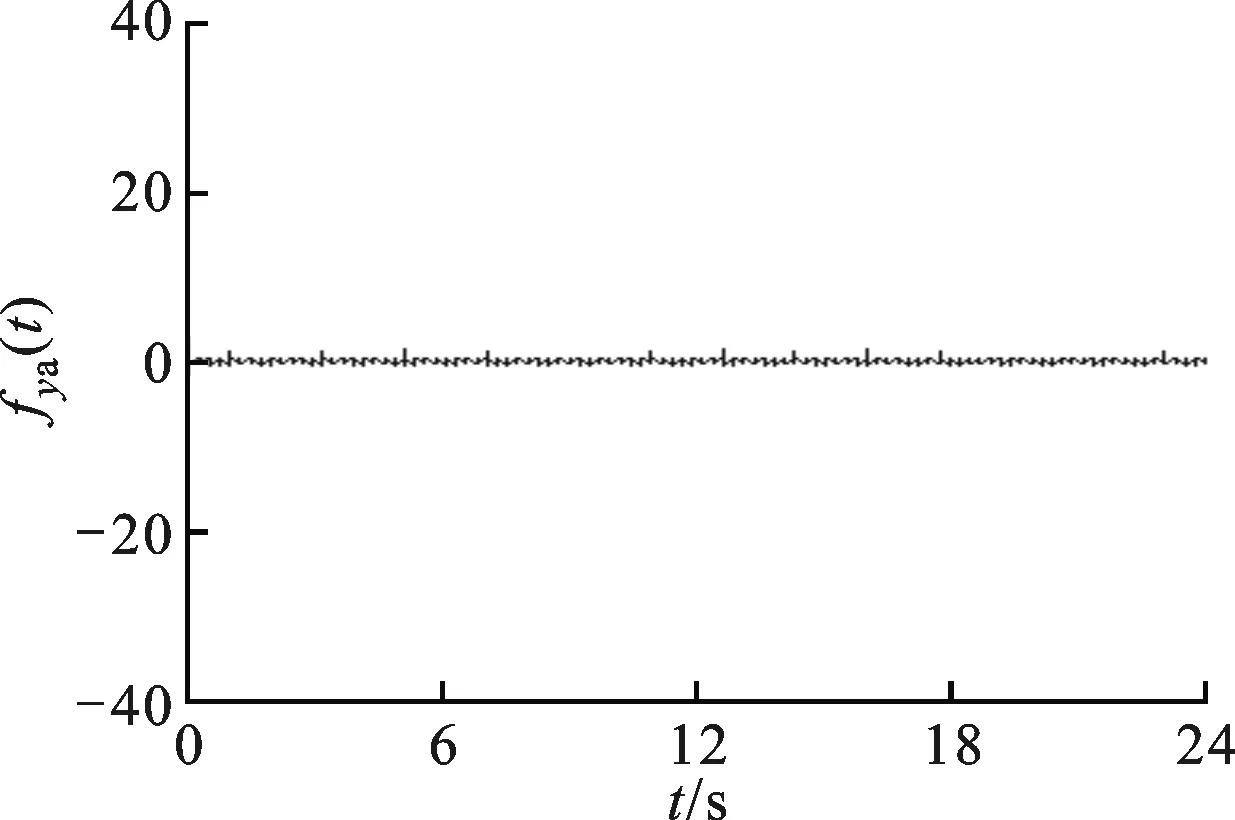
(f)y通道反向滤波后信号

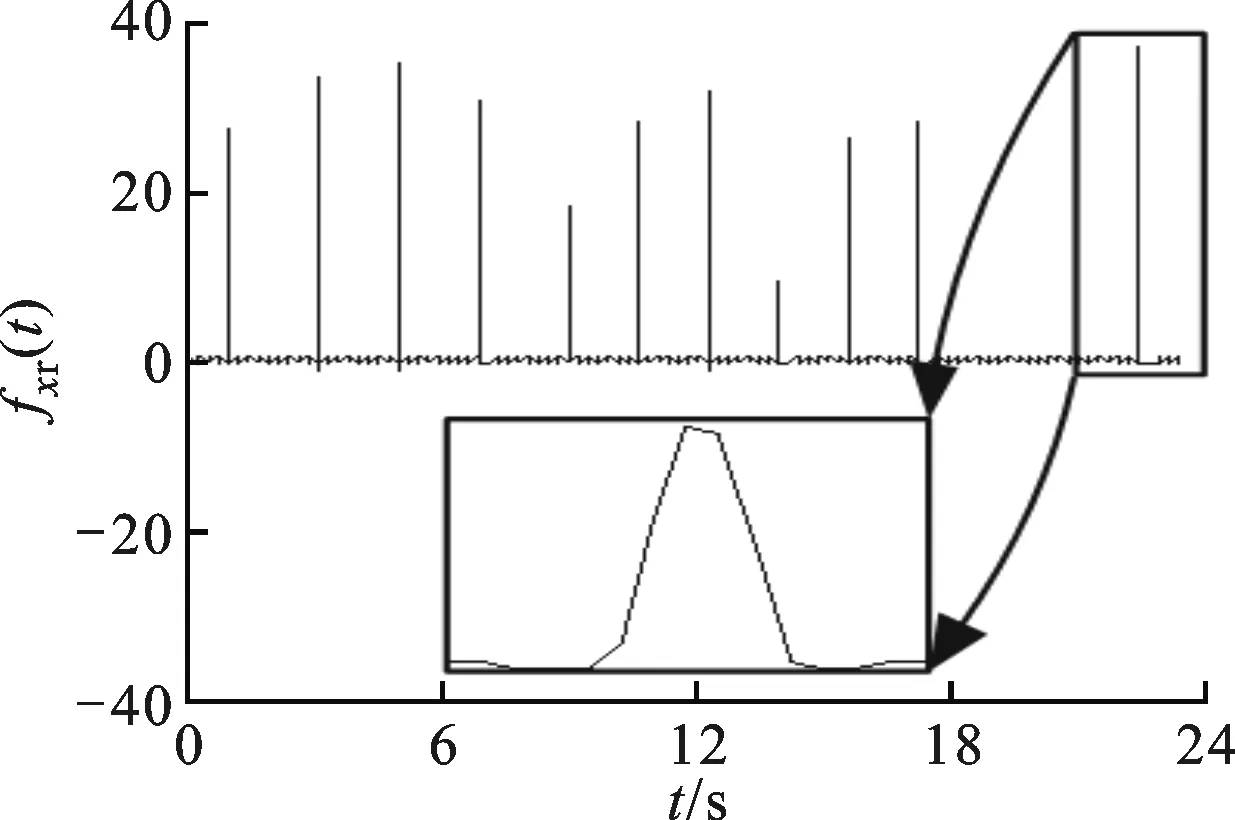
(g)x通道反向滤波和相位补偿后信号

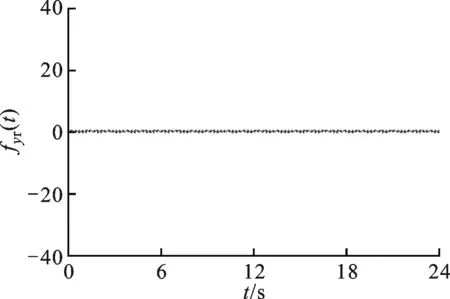
(h)y通道反向滤波和相位补偿后信号图7 动态力信号测试与补偿结果

5 结 论

本文分析了动态力测试系统的结构动态特性对测试信号的干扰,采用反向滤波的原理对动态力测试信号进行修正。基于单输入单输出最小相位传递函数设计方法,设计了多输入多输出最小相位传递函数矩阵,并应用于动态力测试结果的滤波补偿。实验结果表明,基于最小相位传递函数提出的反向滤波器可以对动态力信号测试结果进行有效的修正。经反向滤波补偿后的测试结果与真实输入值相对误差小于6%。

测力系统传递函数的测试和参数识别过程中存在误差,将影响反向滤波器组的补偿精度。因此,在使用本文提出的动态力测试信号补偿方法时,应该按照实际需要来提高测力系统传递函数测试精度。

[1] PARK S S, ALTINTAS Y. Dynamic compensation of spindle integrated force sensors with Kalman filter [J]. Journal of Dynamic Systems, Measurement and Control, 2004, 126(3): 443-452.

[2] ALBRECHT A, PARK S S, ALTINTAS Y, et al. High frequency bandwidth cutting force measurement in milling using capacitance displacement sensors [J]. International Journal of Machine Tools and Manufacture, 2005, 45(9): 993-1008.

[3] 田红亮, 赵春华, 朱大林, 等. 整个螺栓结合部的法向连接动刚度及试验验证 [J]. 西安交通大学学报, 2012, 46(9): 31-36. TIAN Hongliang, ZHAO Chunhua, ZHU Dalin, et al. Analysis and validation on normal connection dynamic stiffness of bolted joint interface ensemble [J]. Journal of Xi’an Jiaotong University, 2012, 46(9): 31-36.

[4] EHMANN K F, KAPOOR S G, DEVOR R E, et al. Machining process modeling: a review [J]. Journal of Manufacturing Science and Engineering, 1997, 119(4B): 655-663.

[5] TOTIS G, WIRTZ G, SORTINO M, et al. Development of a dynamometer for measuring individual cutting edge forces in face milling [J]. Mechanical Systems and Signal Processing, 2010, 24(6): 1844-1857.

[6] TOTIS G, SORTINO M. Development of a modular dynamometer for triaxial cutting force measurement in turning [J]. International Journal of Machine Tools & Manufacture, 2011, 51(1): 34-42.

[7] TRANSCHEL R, STIRNIMANN J, BLATTNER M, et al. Effective dynamometer for measuring high dynamic process force signals in micro machining operations [C]∥5th CIRP Conference on High Performance Cutting. Amsterdam, Holland: Elsevier Science BV, 2012: 558-562.

[8] TLUSTY J, JANG D Y, TARNG Y S. Measurement of the milling force over the wide approved dynamic response [C]∥15th North American Manufacturing Research Conference. Bethlehem, Pennsylvania, USA: Society of Manufacturing Engineers, 1987: 273-280.

[9] CHUNG Y L, SPIEWAK S A. A model of high performance dynamometer [J]. Journal of Manufacturing Science and Engineering, 1994, 116(3): 279-288.

[10]MAGNEVALL M, LUNDBLAD M, AHLIN K, et al. High frequency measurements of cutting forces in milling by inverse filtering [J]. Machining Science and Technology, 2012, 16(4): 487-500.

[11]田红亮, 刘芙蓉, 方子帆, 等. 引入各向同性虚拟材料的固定结合部模型 [J]. 振动工程学报, 2013, 26(4): 561-573. TIAN Hongliang, LIU Furong, FANG Zifan, et al. Immovable joint surface’s model using isotropic virtual material [J]. Journal of Vibration Engineering, 2013, 26(4): 561-573.

[12]PANDIT S M, WU S M. Time series and system analysis with applications [M]. New York: John Wiley and Sons, 1983.

[13]陈淑珍, 杨涛. 零相移滤波器的改进及实现方法 [J]. 武汉大学学报: 理学版, 2001, 47(3): 373-376. CHEN Shuzhen, YANG Tao. Improvement and realization of the zero-phase filter [J]. Journal of Wuhan University: Natural Science, 2001, 47(3): 373-376.

[本刊相关文献链接]

韦兆碧,杨银堂,马志瀛,等.聚磁式光学电流互感器饱和特征的记忆效应补偿研究.2013,47(6):97-102.[doi:10.7652/xjtuxb201306017]

梁新合,梁晋,郭成,等.散乱点云的补偿滤波.2011,45(11):91-94.[doi:10.7652/xjtuxb201111017]

何英杰,刘进军,王兆安,等.三电平有源电力滤波器谐波电流跟踪无差控制方法.2009,43(8):90-94.[doi:10.7652/xjtuxb200908019]

袁敞,刘进军,王晓钰,等.一种新型串联型有源电力滤波器无谐波检测控制方法.2009,43(2):86-89.[doi:10.7652/xjtuxb200902019]

王小龙,水鹏朗,孙晓云.近似完全重构交替离散傅里叶变换调制滤波器组.2008,42(8):1001-1005.[doi:10.7652/xjtuxb200808016]

任品毅,权良辉.多输入多输出系统中基于多级维纳滤波的均衡算法.2008,42(2):218-221.[doi:10.7652/xjtuxb2008 02020]

王风华,韩九强.一种Log-Gabor滤波结合特征融合的虹膜识别方法.2007,41(8):889-893.[doi:10.7652/xjtuxb2007 08003]

(编辑 杜秀杰)

Multi-Channel Dynamic Force Measurement and Compensation with Inverse Filter

ZHU Ming,MAO Kuanmin

(School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

To eliminate the influence of structural dynamics of dynamometer on measurement accuracy of dynamic force, an inverse filter method is considered to modify dynamic signals of the measurement system. Following the theory of the minimum-phase system, an inverse filter with multi-input and multi-output is designed, and an inverse filter matrix is established to compensate the cross-interference between dynamic forces in different directions. The frequency response matrix of the excitation force and measured one is used to model the system dynamics and to transfer into a minimum-phase system. Inverting the minimum-phase transfer function matrix, the inverse filter matrix is obtained. The simulation and experiment show that the magnitude of the measured dynamic force matches well with that of the actual dynamic force. Zero-phase filtering effectively eliminates the phase delay and the relative errors are controlled within 6%.

dynamometer; inverse filtering; minimum phase; frequency response function

2014-06-12。

朱明(1985—),男,博士生;毛宽民(通信作者),男,教授,博士生导师。

国家科技支撑计划资助项目(2014BAF08B01);国家“863计划”资助项目(2012AA040703)。

时间:2014-12-24

10.7652/xjtuxb201502020

TH113.1;TN713

A

0253-987X(2015)02-0117-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141224.1607.002.html