利用异结构同步对铁磁混沌电路的非线性反馈控制
2015-12-26庞霞刘凌刘崇新董子晗
庞霞,刘凌,刘崇新,董子晗
(西安交通大学电气工程学院,710049,西安)
利用异结构同步对铁磁混沌电路的非线性反馈控制
庞霞,刘凌,刘崇新,董子晗
(西安交通大学电气工程学院,710049,西安)
为了抑制变电站中由电压互感器引起的铁磁混沌振荡问题,提出了一种异结构同步的非线性反馈控制方法设计控制器。该方法构造了一个正定的李雅普诺夫函数,使其随时间的导数定负,并将基于李雅普诺夫函数构造的控制器外加在状态方程中,选择状态变量磁链为输出信号,并使该输出信号追踪正弦参考信号,要求误差信号趋于零值。为使控制信号在实际中易于提取,在控制器中用电流替换磁链进行改进。数值仿真结果表明,加入控制器后,系统输出磁链(标幺值)由5降到近似1,电压(标幺值)由17的非周期过电压降到近似1的正弦稳态值。改进控制器后的系统输出电压也由非周期过电压过渡为周期性正弦电压,且电压幅值大大降低,研究结果证明了该控制方法的有效性。
铁磁混沌;非线性;混沌控制
铁磁谐振是电力系统中的一种非线性电气现象,人们对铁磁谐振研究始于20世纪初,数十年来,人们对铁磁谐振从理论分析、实验以及计算机仿真等方面进行了大量的研究。有学者发现,在由变压器或者互感器等非线性电感元件饱和引起的谐振中出现分频信号,该分频信号用线性理论无法解释,只能通过非线性动力学中的分岔理论解释。Kieny于1991年首先在铁磁谐振中观察到混沌现象,之后学者们进行了相关探索[1-3]。近年来,应用混沌理论分析铁磁谐振中的分形和混沌现象是比较热门的研究内容[4-8],但就电力系统中铁磁混沌抑制的工作还需广泛开展。
铁磁混沌是铁磁谐振的一种,呈现非周期振荡特性。在中性点不接地的配网变电站中含有电磁式电压互感器(PT),PT的励磁电感在某些操作中受到冲击会饱和,饱和的励磁电感与母线对地电容参数匹配可能形成非线性谐振系统,该局部非线性系统就可能会产生分岔和混沌振荡[9]。铁磁混沌振荡会产生比周期性振荡更高的过电压,可能会烧毁互感器等设备,或导致设备外绝缘闪络、爆炸等严重事故的发生。近年来,由于PT引起的变电站铁磁谐振时有发生,温州巨溪变电站[10]35 kV母线因电压互感器发生铁磁振荡。某发电厂厂用变电站[11]6 kV系统因铁磁谐振造成PT烧毁导致厂用电停电事故,浙江部分变电站[12]35 kV侧因电压互感器发生铁磁谐振烧坏高压熔丝等。
为了减少铁磁混沌过电压所带来的危害,对电力系统中PT饱和所产生的铁磁混沌的抑制工作显得较为迫切。近年来,国内学者对铁磁混沌的抑制已进行了很多相关研究[13-15],文献[13]考虑时滞因素对铁磁谐振的影响,设计了一种脉冲时滞同步抑制铁磁谐振的方法;文献[14]采用改进的径向基函数神经网络对中性点直接接地系统的铁磁混沌控制进行研究;文献[15]基于常值脉冲法研究了铁磁混沌的抑制,并证实了其有效性。
以上对铁磁混沌的研究大多集中在中性点直接接地系统上,本文对中性点非直接接地系统的铁磁混沌电路进行仿真,并提出一种基于李雅普诺夫函数的异结构同步非线性反馈混沌控制方法,控制本文提出模型中的铁磁混沌,以期为实际铁磁混沌的抑制提供理论指导。
1 铁磁混沌模型
1.1 理论模型
本文研究了刘崇新教授提出的一个由实际变电站接线图简化而来的含有非线性电感的三阶非自治铁磁混沌电路[16],如图1所示。图中n=N1/N2,N1、N2为互感器原、副边线圈的匝数,电路激励为正弦交流电压源u(t)=sin(ωt),C1、C2、R1、R2均为线性元件。
对于电磁式电压互感器,其电感为非线性的,当激励的幅值增大到一定值时,线圈磁通链会饱和,其电流与磁通的关系用奇次方多项式拟合
i3=aψ3+bψ
(1)
式中:a=1;b=1。

R1为电源内阻;R2为母线电阻;C1和C2均为母线对地电容图1 铁磁混沌电路
对于图1,列写方程可得
(2)
(3)
再令x=φ,y=uC1/ω,z=uC2/ω,α=1/(ωC1R2),β=1/(ωC2R2),ζ=1/(ω2C1),η=1/(ωC2R1),F=Um/(ω2C2R1),μ=(β+η),则可得状态方程
(4a)
(4b)
(4c)
当Fsinτ为0时,式(4)为非线性自治系统,其原点为平衡点。当Fsinτ不为0时,Fsinτ为周期函数,故增加一个时间维,式(4)改写为一个四阶自治方程,即为一个等价扭扩系统,相应的方程如下
(5)
式中:θ=τ+τ0。t作为一个新的独立变量,该四维系统有4个独立变量(x,y,z,τ)。在一定的参数条件下,当电源的幅值F达到一定值时,这个四阶自治等价扭扩系统即出现混沌。文献[13]对该系统的混沌动力学特性进行了详细分析,文献[9]还研究了电压互感器的励磁特性对该电路的铁磁混沌的影响。
1.2 数值仿真
在相空间中,稳态系统对应于一点,周期态对应于封闭曲线,混沌运动则对应于一定区域内随机分离的永不封闭的轨迹。根据动力学系统的数值计算结果,画出相空间中相轨迹随时间变化的相图,通过对比分析以确定系统的分岔和混沌现象。
设置参数ζ=0.65,α=0.25,β=0.13,η=0.65,C1=1.56×10-5F,C2=3×10-5F,R1=163.3 Ω,R2=816.6 Ω。

(a)三维相图

(b)x-y相图图2 F=260.80时铁磁混沌系统的相图
图2为铁磁混沌系统数值仿真的x-y相图和x-y-z三维相图,其相图为奇怪吸引子,呈现了混沌振荡的基本特性。图3为F=260.8、z=0截面的庞加莱映射图,证明F=260.8时系统出现了混沌。图2和图3中的数值均以标幺值表示。

图3 F=260.8时z=0截面的庞加莱映射
图4所示为随F变化的李雅普诺夫指数谱。当存在正的李雅普诺夫指数时,系统为混沌振荡状态。图4显示激励F=19时,李雅普诺夫指数第一次出现正值L1=0.003 535,L2=0,L3=-0.246 4,L4=-0.787 0,系统出现混沌振荡。当F=73时,最大李雅普诺夫指数为0.030 45;当F=75时,最大李雅普诺夫指数为0.088 63。F在区间(231,282)中,系统处于混沌振荡状态。当F=260.8时,L1=0.124 7,L2=0,L3=-0.372 0,L4=-0.782 7,李雅普诺夫维数为
李雅普诺夫维数为分数维数,且存在正的李雅普诺夫指数,故该系统出现了混沌振荡。

图4 随F变化的李雅普诺夫指数谱
2 铁磁混沌控制
由于混沌运动对初始值极端敏感,故从任意靠近的两个初始值出发的轨道在一定的时间区间内都会以指数形式分离。系统初始值极其微小的差异都能够使系统的振荡输出产生本质的变化。
图5是混沌状态下x和y的时域信号图,其值为标幺值。从图中可以看到,铁磁混沌使得电压急剧增加,电流大幅度上升,可能导致电压互感器烧毁、外绝缘闪络等严重事故的发生,严重危害电力输变电网络运行的可靠性和安全性,故针对电力系统中PT饱和所产生的混沌状态的抑制显得较为迫切。
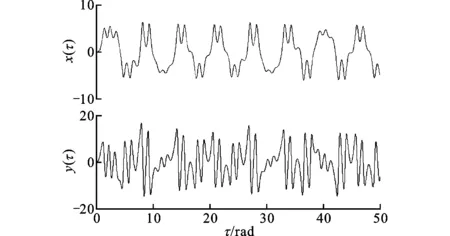
图5 混沌状态的时域信号图
在系统分析中,从数学方面来考虑,经常借助于构造一个李雅普诺夫函数V(x,y)来进行辅助分析。李雅普诺夫判断系统零解稳定性的思想是:利用V(x,y)及通过方程组得到全导数dV(x,y)/dt来帮助确定系统零解是否具有稳定性。
对于任一描述非线性动力学系统的微分方程dx/dt=f(x),若存在一个正定的函数V(x),且函数V(x)关于方程dx/dt=f(x)的全导数dV/dt是定负的,那么该非线性动力学系统的零解则是渐近稳定的。这是由于导数dV/dt<0,其函数V(x)随时间得到变化率是定负的,因此函数V(x)随时间t的增大而不断减小,这时方程的轨线就一直穿过闭曲线族V(x)=C,因而系统的响应x(t)最终会趋于零解。

于是式(4b)变为
(6)


(7)

(8)
这样就使
(9)
(10)
e(τ)=x(τ)-r(τ)
(11)

(12)
把式(10)~式(12)代入式(8),得
(13)
于是,得到加控制量后的系统方程
(14a)
(14b)
(14c)
假定要追踪的参考信号为r(τ)=sin(τ)。图6是该系统加控制量后的状态变量x和y的时域信号及误差曲线,其值为标幺值。对比图5与图6可得,铁磁混沌振荡的时域波形是非周期的,且磁链x(τ)幅值(标幺值)约为5,电压y(τ)的幅值(标幺值)约为17;加控制器后的系统波形图均为周期的,磁链和电压的波形幅值(标幺值)均为1,误差信号呈指数衰减,约一个周期内就趋于0,该控制器较好地追踪了给定的目标信号。

图6 加控制量后的时域信号及误差信号
在实际应用中,由于x的物理含义是磁链,它不易测得,故要考虑使用近似量代替,还不能影响控制的效果。因为x要追踪的是给定信号r,即若干时间后x与r的误差很小,而ax3+bx是电流i3的大小,容易提取,故对式(13)作如下修改,目的在于在u(τ)的表达式中用ax3+bx来取代x项

ζ(ax3+bx)+a(r3-x3)+(b-1)(r-x)=
(ζ-1)(ax3+bx)
(15)


(16)


改进后的误差函数曲线如图7所示,其值为标幺值。以实际应用为目的,用容易获得的电流量代替不易获得的磁链改进控制器。与图5比较,加控制器后系统的波形由非周期变为周期波形,且幅值大大降低,误差信号呈指数衰减,不到两个周期就可衰减趋于0。

图7 改进后的误差曲线
通过构造正定的李雅普诺夫函数,并使其随时间的导数为定负的,得到异结构同步的非线性反馈控制器。给定参考信号r(τ),在图1所示电路的C1支路并接一个独立电流源,其值由式(15)决定,并用断路器控制其通断,如图8所示,在出现过电压的情况下接通该电流源,可有效地防止铁磁谐振过电压带来的危害。对该控制器进行了改进,使其能更好地应用到实际中。

图8 铁磁混沌控制的实现
3 结 论
本文针对实际变电站的接线情况建模,由电路模型推导出其数学模型,通过数值仿真得到该模型的吸引子相图、庞加莱映射和李雅普诺夫指数谱,还发现该电路模型确实存在铁磁混沌振荡。为控制该电路中的铁磁混沌,本文提出了一种基于李雅普诺夫函数的异结构同步非线性反馈控制方法构造控制器,使系统的状态变量可以追踪任一目标信号。由于磁链不易获得,对原控制器进行改进,用容易获得的电流替换原控制器中的磁链,使其能够应用于实际。外加控制器后,系统状态变量的时域波形由非周期波形变为周期波形,且幅值大大降低,基本为正常运行值,且误差曲线呈指数衰减至0。
[1]MARTI R.Ferroresonance in power systems:fundamental solutions [J].IEE Proceedings:C, 1991, 138(4):321-329.
[2]EMIN Z, AL ZAHAWI B A T, TONG Y K, et al.Quantification of the chaotic behavior of ferroresonant voltage transformer circuits [J].IEEE Trans on Circuit and Systems, 2001, 48(6):757-760.
[3]KIENY C.Application of the bifurcation theory in studying and understanding the global behavior of a ferroresonant electric power circuit [J].IEEE Trans on Power Delivery, 1991, 6(2):866-872.
[4]HUI Meng, ZHANG Yanbin, LIU Chongxin.Chaotic ferroresonance in a non-autonomous circuit [J].Chinese Physics:B, 2008, 17(9):3258-3263.
[5]刘凡, 孙才新, 司马文霞, 等.铁磁谐振过电压混沌振荡的理论研究 [J].电工技术学报, 2006, 21(2):103-107.LIU Fan, SUN Caixin, SIMA Wenxia, et al.Theoretical analysis of chaotic oscillation of ferroresonance overvoltage in power systems [J].Transactions of China Electrotechnical Society, 2006, 21(2):103-107.
[6]司马文霞, 陈莉珺, 杨庆, 等.GTO控制阻尼电阻脉冲投入的铁磁谐振控制 [J].高电压技术, 2014, 40(5):1520-1529.SIMA Wenxia, CHEN Lijun, YANG Qing, et al.Ferroresonance control through GTO controlling damping resistance pulsed access [J].High Voltage Engineering, 2014, 40(5):1520-1529.
[7]GHOLIZADEH H, HASSANNIA A, AZARFAR A.Chaos detection and control in a typical power system [J].Chinese Physics:B, 2013, 22(1):010503.
[8]HUI Meng, ZHANG Yanbin, LIU Chongxin.Analysis of ferroresonance in neutral grounding system with nonlinear coreloss [J].Chinese Physics:B, 2009, 18(5):1787-1791.
[9]庞霞, 刘崇新.含电磁式电压互感器的铁磁混沌电路的分析研究 [J].物理学报, 2013, 62(15):150504.PANG Xia, LIU Chongxin.Analysis of ferromagnetic chaotic circuit with nonlinear potential transformer [J].Acta Phys Sin, 2013, 62(15):150504.
[10]王胜, 赵意合, 蔡建辉, 等.电压互感器铁磁谐振防范措施 [J].农村电气化, 2014(1):61.WANG Sheng, ZHAO Yihe, CAI Jianhui, et al.Precautions of voltage transformer ferroresonance [J].Rural Electrification, 2014(1):61.
[11]武文杰, 王忠为.厂用6 kV系统铁磁谐振分析及措施研究 [J].自动化与仪器仪表, 2011(3):13-14.WU Wenjie, WANG Zhongwei.Analysis and measures of ferroresonance in plant 6 kV system [J].Automation & Instrumentation, 2011(3):13-14.
[12]赵晓明, 余志慧.500 kV主变35 kV侧铁磁谐振实例及其数值仿真分析 [J].浙江电力, 2008(3):23-25, 47.ZHAO Xiaoming, YU Zhihui.Instances and numerical simulation of ferroresonance in 35 kV side of 500 kV main transformer [J].Zhejiang Electric Power, 2008(3):23-25, 47.
[13]惠萌, 刘盼芝, 白璘, 等.非自治铁磁谐振电路过电压脉冲时滞同步抑制方法研究 [J].西安交通大学学报, 2014, 48(6):55-59.HUI Meng, LIU Panzhi, BAI Lin, et al.Overvoltage suppression by impulsive time-lagging synchronization of non-autonomous ferroresonance chaotic circuit [J].Journal of Xi’an Jiaotong University, 2014, 48(6):55-59.
[14]司马文霞, 刘凡, 孙才新, 等.基于改进的径向基函 数神经网络的铁磁谐振系统混沌控制 [J].物理学报, 2006, 55(11):5714-5720.SIMA Wenxia, LIU Fan, SUN Caixin, et al.Chaos control of ferroresonance system based on improved RBF neutral network [J].Acta Phys Sin, 2006, 55(11):5714-5720.
[15]刘凡, 司马文霞, 孙才新, 等.基于常值脉冲法的铁磁谐振过电压混沌抑制 [J].电网技术, 2006, 30(3):57-61.LIU Fan, SIMA Wenxia, SUN Caixin, et al.Controlling chaos in ferroresonance overvoltage based on constant pulse method [J].Power System Technology, 2006, 30(3):57-61.
[16]刘崇新, 翟笃庆, 董子晗, 等.含有单相铁心变压器的铁磁混沌电路的分析及控制 [J].物理学报, 2010, 59(6):3733-3739.LIU Chongxin, ZHAI Duqing, DONG Zihan, et al.Control and analysis of a third-order nonautonomous ferroresonance chaotic circuit with a transformer [J].Acta Phys Sin, 2010, 59(6):3733-3739.
[本刊相关文献链接]
惠萌,刘盼芝,白璘,等.非自治铁磁谐振电路过电压脉冲时滞同步抑制方法研究.2014,48(6):55-59.[doi:10.7652/xjtuxb201406010]
傅文渊,凌朝东.自适应折叠混沌优化方法.2013,47(2):33-38.[doi:10.7652/xjtuxb201302006]
赵志斌,孙跃,周诗杰,等.非接触电能传输系统参数优化的改进遗传解法.2012,46(2):106-112.[doi:10.7652/xjtuxb 201202018]
吴沁,芮执元,杨建军.考虑非线性弹性力的滚珠丝杠系统分岔与混沌特性分析.2012,46(1):70-75.[doi:10.7652/xjtuxb201201013]
薛士明,曹军义,林京,等.分数阶阻尼裂纹转子的非线性动力学特性分析.2012,46(1):76-80.[doi:10.7652/xjtuxb 201201014]
孙清,张斌,伍晓红,等.时滞受控系统非线性动力学行为的数值分析.2011,45(3):1-6.[doi:10.7652/xjtuxb201103001]
付华,乔德浩,池继辉.一种非线性系统参数辨识的耦合算法研究.2011,45(2):49-53.[doi:10.7652/xjtuxb201102010]
罗勇芬,黄平,李彦明.油纸绝缘中局部放电时间序列的混沌特性及其模式识别.2010,44(12):55-60.[doi:10.7652/xjtuxb201012011]
汪伟,汲胜昌,李彦明.用非线性电阻模拟变压器损耗进行铁磁谐振过电压研究.2009,43(10):109-113.[doi:10.7652/xjtuxb200910023]
宋青松,冯祖仁.构建复杂回响状态网络的新方法.2009,43(4):1-4.[doi:10.7652/xjtuxb200904001]
曹军义,谢航,蒋庄德.分数阶阻尼Duffing系统的非线性动力学特性.2009,43(3):50-54.[doi:10.7652/xjtuxb200903 011]
刘芳.电流型单端初级电感变换器的不稳定性与分岔控制.2007,41(12):1465-1469.[doi:10.7652/xjtuxb200712018]
王晶,高金峰,马西奎.同步一类结构部分未知混沌系统的自适应非线性观测器.2007,41(10):1165-1169.[doi:10.7652/xjtuxb200710009]
张旭东,熊静琪,王丛岭.基于遗传算法信息组合的自适应模糊控制.2007,41(7):838-841.[doi:10.7652/xjtuxb200707 019]
逯俊杰,刘崇新,张作鹏,等.基于状态观测器的分数阶统一混沌系统的同步控制.2007,41(4):497-500.[doi:10.7652/xjtuxb200704026]
郭振宇,程博,叶敏,等.一种并行混沌差异演化算法.2007,41(3):299-302.[doi:10.7652/xjtuxb200703008]
(编辑 杜秀杰)
Nonlinear Feedback Control in Ferromagnetic Chaotic Circuit with Different Structure Synchronization
PANG Xia,LIU Ling,LIU Chongxin,DONG Zihan
(School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
To suppress the ferromagnetic chaotic oscillation from voltage transformer in substations, a nonlinear feedback control strategy with different structure synchronization is proposed to design the controller.A positive definite Lyapunov function with negative definite derivative over time is constructed, and the tentative controller takes part in the state equation, where the flux serves as the output signal to track sinusoidal reference signal to keep error signal as zero.For the purpose of easy extracting, the current is chosen instead of the flux.The numeric simulation shows that once adding the controller, the system flux decreases from 5 p.u.to 1 p.u., and voltage decreases from non-periodic overvoltage of 17 p.u.to steady sinusoidal value of 1 p.u., and the previous non-periodic overvoltage output can be transformed into periodic sinusoidal voltage with greatly reduced amplitude.
ferromagnetic chaos; nonlinear; chaos control
2014-07-09。 作者简介:庞霞(1989—),女,硕士生;刘凌(通信作者),男,讲师。 基金项目:国家自然科学基金资助项目(51177117,51307130);教育部高等学校博士学科点专项科研基金资助项目(20100201110023)。
时间:2014-10-31
http:∥www.cnki.net/kcms/detail/61.1069.T.20141031.1642.012.html
10.7652/xjtuxb201504004
TM132
A
0253-987X(2015)04-0018-06
