调节阀内流型分布及利用声音突变判别流型转变的方法

曾立飞,刘观伟,毛靖儒,袁奇,王朝阳,魏龙,张俊杰,徐亚涛

(西安交通大学叶轮机械研究所,710049,西安;2.神华国华(北京)电力研究院有限公司,100025,北京)



调节阀内流型分布及利用声音突变判别流型转变的方法

曾立飞1,刘观伟1,毛靖儒1,袁奇1,王朝阳1,魏龙1,张俊杰2,徐亚涛2

(西安交通大学叶轮机械研究所,710049,西安;2.神华国华(北京)电力研究院有限公司,100025,北京)

针对流体诱发调节阀振动和噪声而影响汽轮机安全、稳定运行的问题,结合实验和数值模拟研究了阀内流型分布及流型与噪声、振动的关系。研究表明:在中小升程下调节阀内存在2种流型,其中附阀座流相对于冲击射流是一种更加稳定且噪声较小的流型;不同压比调节方式下,即使同一工况也会出现这2种流型;连续改变压比会出现一种声音突变现象,该现象由附阀座流和冲击射流的转变所致;利用声音突变可以确定调节阀在中小升程下流型区域的分布范围,可为判断数值模拟所得流型的正确性提供参考。

调节阀;流型;振动;数值模拟

汽轮机启停和功率变化是通过调节阀开度的变化改变进入汽轮机的蒸汽流量或蒸汽参数实现的,因此调节阀工作性能的好坏直接关系到汽轮机的经济性和运行安全性。在极其残酷的变工况环境中,调节阀是进气系统中最薄弱的环节[1],特别是随着机组容量的不断增大、进气参数的提高,近年来在电厂中由流体诱发调节阀振动而导致的阀杆螺纹滑丝、阀杆断裂[2-3]等事故频发。

调节阀内流动为复杂的三维超声速流动,由流体诱发的调节阀振动与阀内流型密切相关。Heymann指出,调节阀内存在附阀座流和冲击射流2种流型,附阀座流是相对稳定的流型,其诱发的噪声明显小于不稳定的冲击射流[4]。Araki通过二维可视化实验发现,调节阀内存在3种流型,随着压比的减小,流型逐渐变为对称的冲击射流[5]。Tecza结合二维数值模拟和实验发现,调节阀内存在5种流型,其中2种是稳定流型,另外3种为不稳定流型[6]。Clari利用临界点理论指出,相比冲击射流,附阀座流是一种更加稳定的流型[7]。Hardin通过不断改进阀碟型线,将调节阀内的冲击射流转变为附阀座流,最后得到了稳定性较好的阀型[8]。Zhang对某调节阀做了大量的二维定常数值模拟,结果表明,中小升程下阀内不对称流是引起调节阀振动的主因[9]。Morita、Yonezawa等进一步利用三维非定常数值模拟并结合实验指出,中等升程下阀碟下方周向移动的高压区会导致调节阀振动[10-11]。

从以往的研究可以看出,调节阀的振动与阀内流型密切相关,依靠数值模拟准确预测阀内流型已成为分析流体诱发调节阀振动的关键。本文通过实验对调节阀做了大量的工况测试,在连续调节压比的过程中发现了一种声音突变现象。不同的压比调节方式在同一升程下均有2个声音突变压比,在这2个声音突变压比之间的区域,即使是同一工况下也会出现2种流型。本文根据阀内流型分布呈现区域性的特点,提出了利用声音突变来判断阀内流型分布范围的方法。

1 实验设备及方法

图1为调节阀性能测试系统。实验介质为压缩空气,气源由压缩机提供且储存于储气罐内。通过控制旁通阀的开度可以改变调节阀的进口总压,从而达到调节压比的目的,而调节阀的开度通过阀杆上端的提升机构控制。压力测量采用高精度的Rosemount变送器,测量精度可达0.075%,压力测点布置于阀前管道、进口、卸载室、出口;温度测量采用热电偶,测点布置于阀前管道、进口、出口;流量测量采用孔板流量计,测点布置于阀前和阀后,用以相互验证流量。静态测点数据由分散式智能数据采集器(isolated measurement pods, IMP)采集,再经计算机计算实时监测和采集实验系统中的压力、温度、流量和压比等参数。

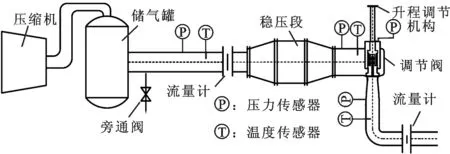
图1 调节阀性能测试系统

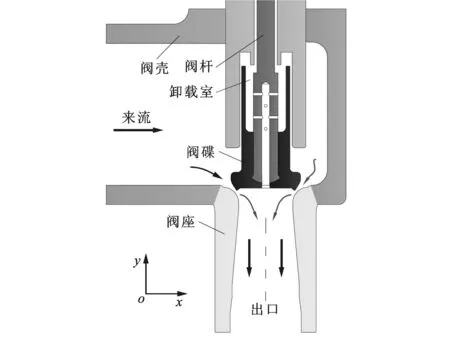
图2 调节阀结构

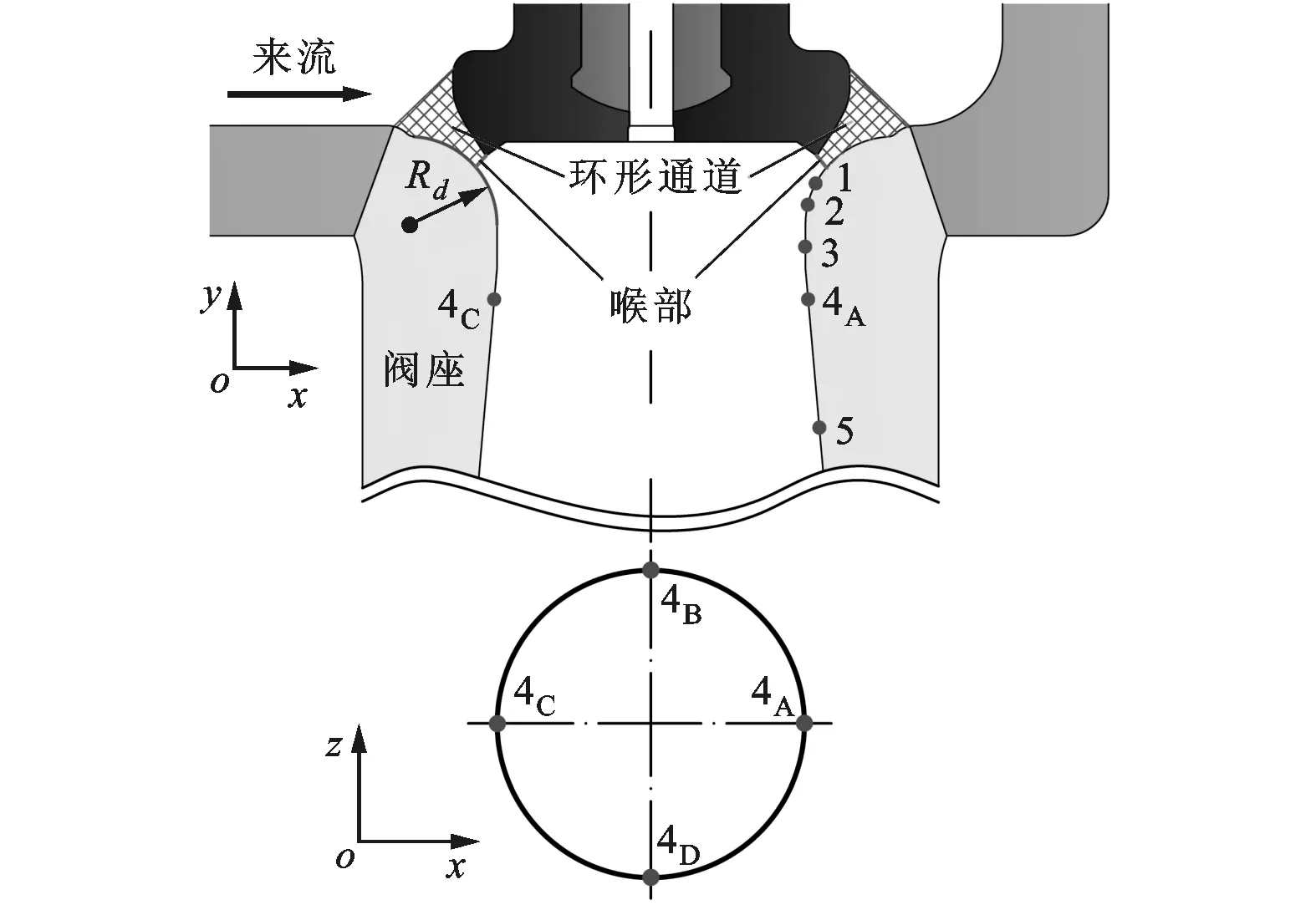
图3 阀座局部结构及动态压力和数值模拟监测点布置

图2为调节阀结构。图3为阀座局部结构及动态压力和数值模拟监测点布置。图3中有4个动态压力测点,2个测点相隔90°且均布于阀座,测点名称分别为4A、4B、4C和4D;数值模拟监测点分别为1、2、3、4A和5。调节阀的工况使用了2个量纲为1的参数:相对升程Hf(调节阀的升程和配合直径之比,配合直径Ds=79.1 mm)和压比ε(出口静压和进口总压之比)。

测试中首先固定调节阀的升程,从相对升程Hf=2.5%开始,然后调节旁通阀改变进口压力,使得压比ε从0.9起逐渐减小(压比测试间隔为0.05),直至压比为0.2,之后提高升程,继续测试下一升程的压比点。在调节压比过程中发现,由调节阀产生的声音会出现一种“突变现象”,即调节阀产生的声音的音量和音色发生明显的突然变化,实验中声音突变前后声压突变的幅值可达5～11 dB。

在固定的调节阀升程中,每一个升程下按照2种压比调节方式进行调节,即从ε=0.9逐渐降低到ε=0.2(调节方式1)和从ε=0.2逐渐升高到ε=0.9(调节方式2),压比改变量约为0.000 5 s-1。在所测的每一个升程下有2个声音突变压比点,测试结果如图4所示。对于2个声音突变压比之间的工况,2种压比调节方式对应2种噪声和压力脉动。

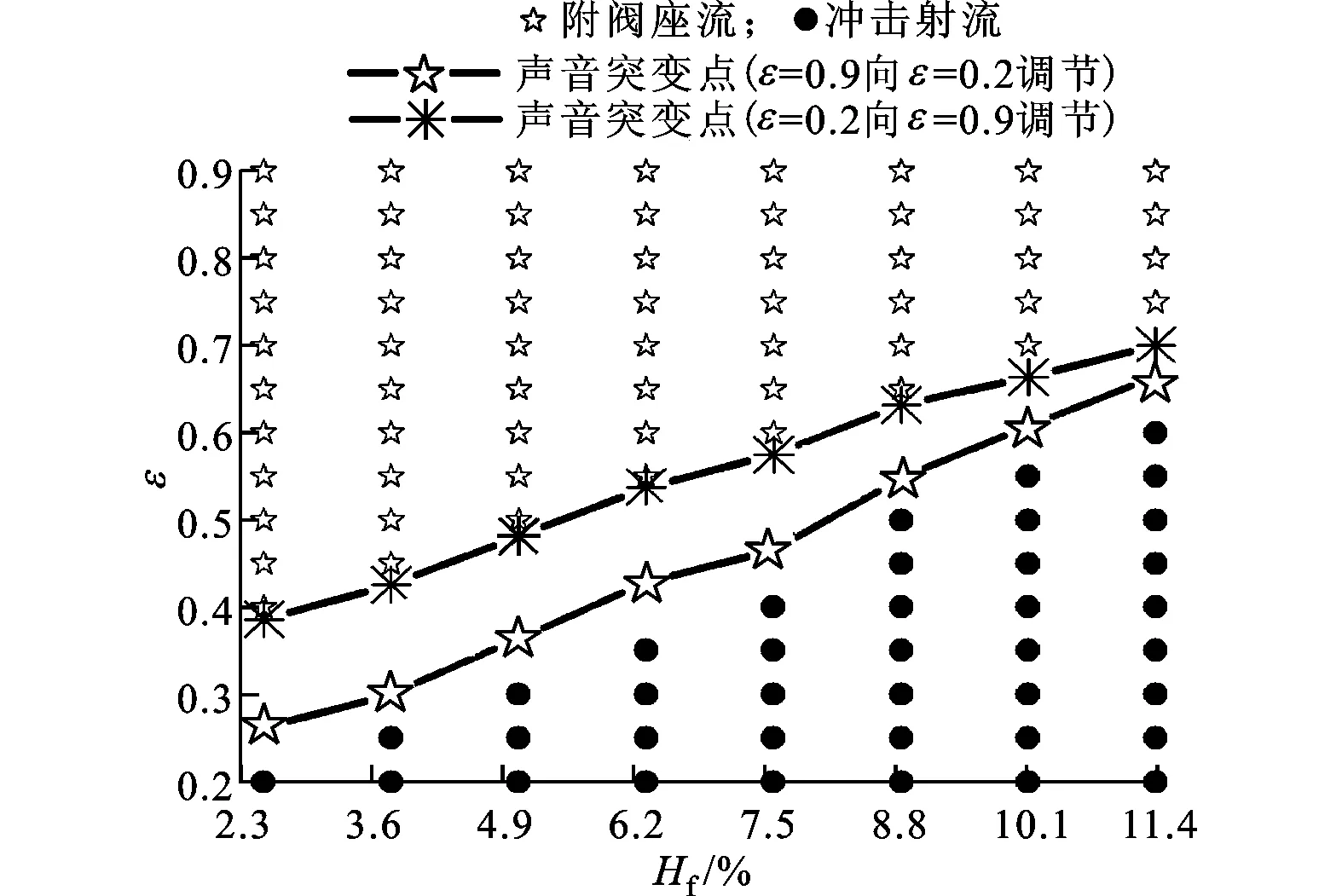
图4 声音突变点和数值计算流型分布图

2 数值模拟

数值模拟借助了Fluent软件,实验工况逐一进行了定常数值模拟。进口设置为总压进口,出口使用静压出口,其他边界均假定为绝热壁面,实验数据均来自于实验测量。湍流模型采用了可实现k-ε模型,近壁面使用了可扩展壁面函数。

各个工况下的数值模拟结果表明,计算所得流量与实验误差在3%以内,卸载室压力误差在5%以内。各工况点的流型分布见图4,当Hf≤11.4%时存在2种典型流型,即冲击射流和附阀座流,2种流型如图5所示。冲击射流特点为高速流体从环形通道流出后在阀座处分离,且以自由射流的形式在阀碟下方汇聚;附阀座流特点为由环形通道流出的大部分流体在靠近阀座壁面的狭小区域内通过,阀座下方大部分区域被低速回流所充斥[4]。

从图4还可以看出,冲击射流在小压比区域内,附阀座流在大压比区域内,在2个声音突变压比之间流型不确定,会受计算采用初场的影响,这一区域定义为数值计算的流型不确定区域。选取这一区域中的工况点Hf=7.6%、ε=0.5,分别利用冲击射流和附阀座流在2种初场进行非定常数值模拟。非定常数值模拟中边界条件的设置与定常计算相同,湍流模型使用了预测分离流较好的基于可实现k-ε的分离涡模拟(DES)模型。DES模型结合了雷诺平均与大涡模拟技术[12-13]的优势:在近壁面的附面层内采用RANS方法,用较小的计算量获得相对理想的壁面特征;在远离物面的区域对大尺度分离流使用大涡模拟技术,可以对分离流进行较好的模拟[13-15]。

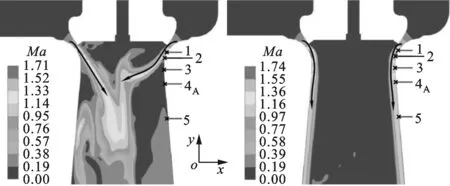
(a)冲击射流 (b)附阀座流图5 Hf=7.6%、ε=0.5、t=0.3 s时的2种典型流型

2.1 调节阀内的2种流型

图6为采用调节方式2且在Hf=7.6%、ε=0.5(计算中选用ε=0.4冲击射流作为初场)时的压力波动时域图。从图中可以看出:实验和数值模拟结果符合较好;在测点4A处的压力波动明显大于其他测点,流型在t=0.2～0.3 s均为冲击射流,这是冲击射流的撞击点在测点4A附近摆动所致。

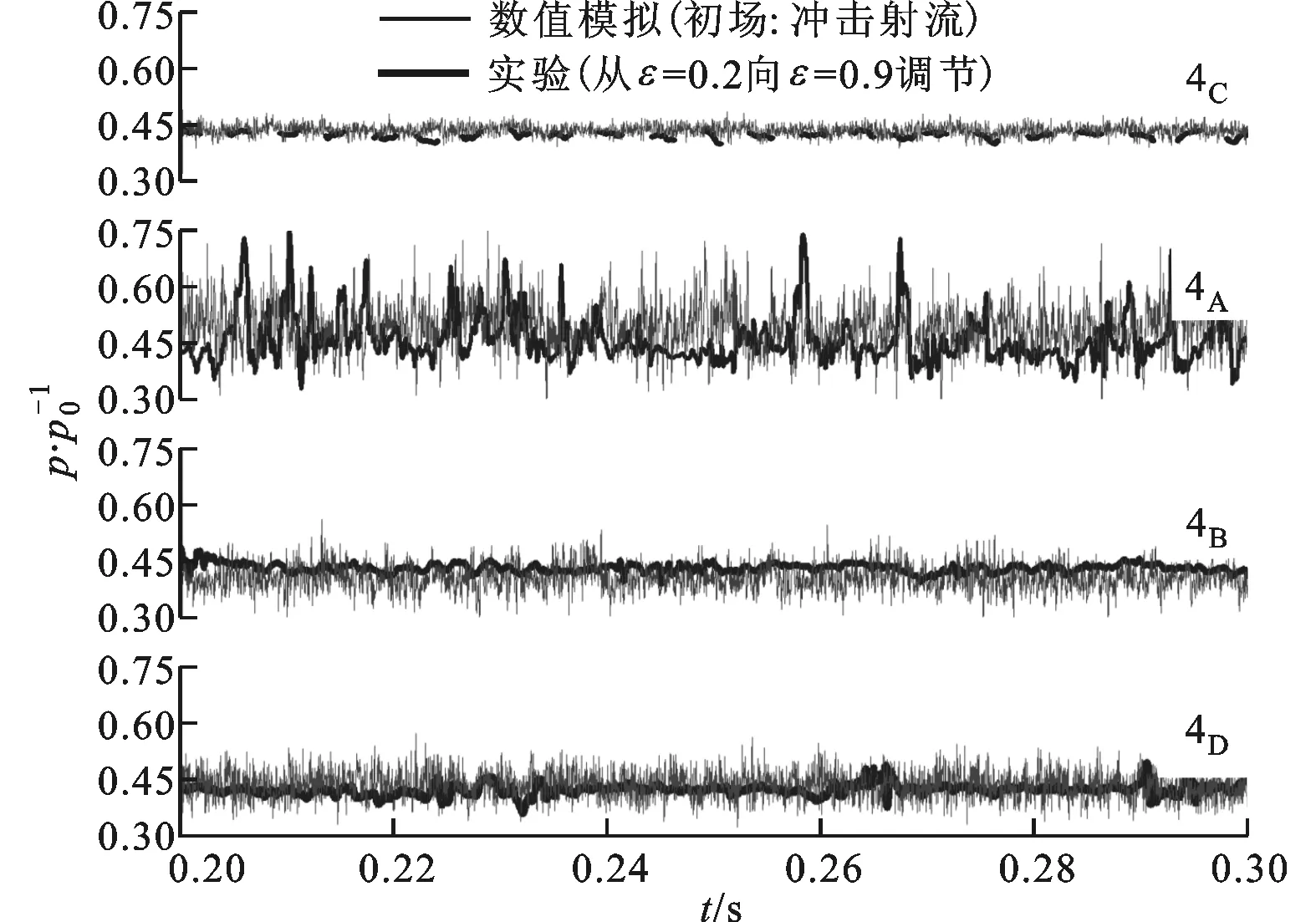
图6 采用调节方式2且在Hf=7.6%、ε=0.5时的压力波动时域图

图7为采用调节方式1且在Hf=7.6%、ε=0.5(计算中选用ε=0.6附阀座流作为初场)时的压力波动时域图。从图中可以看出:数值模拟所得的流型在t=0.2～0.3 s时均为附阀座流;实验和数值模拟在阀座的4个测点的压力波动均小于图6的压力波动。

图7 Hf=7.6%、ε=0.5时实验和数值模拟阀座压力波动时域图(附阀座流)

图8和图9分别是非定常数值模拟工况在Hf=7.6%、ε=0.5所得2种流型下阀座测点1、2、3、4A和5处的压力波动时域图。从图8可以看出,流型为冲击射流时阀座测点2、3和4A的压力波动幅度明显大于测点1、5的压力波动。如图5a所示,从喉部流出的高速射流并没有立即与阀座分离,而是继续附着于阀座,在测点1后才逐渐开始分离,所以测点1处的压力波动类似于图9中附阀座流测点1的压力波动。测点2、3和4A的压力波动较大是由喉部后的高速射流不断离开和靠近壁面所致,而高速射流不断摆动并未影响到阀座下游测点5。喉部出口处的阀座型线曲率半径Rd对高速射流分离阀座起着至关重要的作用,文献[5,16]尝试了增大Rd以获得更加稳定的流型。图9中5个测点处的压力波动量都非常小。对于附阀座流,回流几乎充斥着整个阀座区,由喉部流出的高速射流被约束在很小的区域内且紧贴阀座流动,因而高速流体的波动较小。附阀座流中高速流体相比冲击射流的混合脉动衰减更小,高速流体区域持续到监测点5之后,如图5b所示。Hf=7.6%、ε=0.5时按照IEC标准[17-18]预测阀内噪声,此工况点处于流态Ⅲ(pvcc>pout≥p2B,pvcc为临界流动时最小截面处的压力,pout为阀出口压力,p2B为断点状态的阀出口压力),此时pout已经下降到低于喉部临界压力,其后没有进一步的压力恢复。此流态下的噪声主要由激波与湍流相互作用和湍流剪切应力所产生的噪声所致。当流型为冲击射流时,激波及其反射波与下游的湍流相作用的区域远大于被限制在壁面的附阀座流中激波与湍流相互作用的区域。此外,由图8和图9还可以看出,冲击射流在壁面上的压力波动远大于附阀座流,冲击射流在阀碟下方还形成了撞击,射流本身湍流脉动和撞击不稳定使得由湍流剪切应力造成的噪声相比附阀座流更强。综合以上2点分析,即使在同一工况下,冲击射流的噪声也明显大于附阀座流。

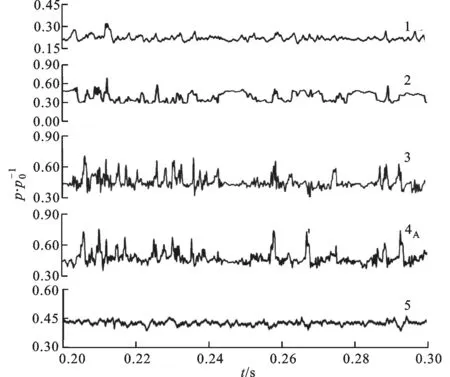
图8 非定常数值模拟阀座各测点压力波动时域图(冲击谢流)

图9 非定常数值模拟阀座各测点压力波动时域图(附阀座流)

2.2 声音突变现象及应用

文献[19]指出,当阀内的流动变为阻塞流时阀内噪声和流型密切相关,而流型与阀的结构、升程及压比相关。在实验中发现,附阀座流噪声比未附着射流低8～10 dB。文献[4,20]指出,附壁流噪声明显小于冲击流噪声。文献[21]还提出了通过改变流道型线使流型由冲击射流转变为附壁流而降低噪声的建议。由图4数值模拟的流型分布可以看出,小压比区域为冲击射流,大压比区域为附阀座流。若采用调节方式1,随着压比的持续增加,必然会在某一压比下发生冲击射流向附阀座流转变;反之,若采用调节方式2,不可避免地会发生附阀座流向冲击射流转变。可以推测,在调节压比的过程中所出现的“声音突变”现象是由冲击射流和附阀座流相互转变所致。由图3可以看出,阀碟下方为凹口型阀,类似的凹口阀型G-I型阀中也发现了声音突变现象[22]。相对于阀碟型线为球形的阀碟,这种凹口型阀更加利于减振[5,8],因而在实际中也得到了较多的应用。

实验和数值模拟结果表明,在图4流型不确定工况区域中,同一工况下可以出现2种流型,这就对数值模拟提出更高的挑战,究竟哪一种流型是调节阀内部的真实流型,需要先确定调节阀内流型在不确定区域的分布范围。实验中,利用连续调压比产生的声音突变现象可以确定这一区域。若使用纹影仪或PIV等方法可以准确验证阀内流型,但实验操纵难度较大且需耗费较多的精力。此外,文献[5,22-23]的研究表明,在中小升程下调节阀内的流型呈现类似图4中的区域性分布特征,即在小压比范围内为冲击射流,在大压比范围内为附阀座流。因此,考虑到中小升程下阀内流型的这种分布特征,可以利用声音突变现象作为一种简单且实用的实验方法,来判断数值模拟所得流型分布的正确性。

3 结 论

本文在连续调节压比的过程中发现了声音突变现象,结合数值模拟分析得出声音突变现象是由附阀座流和冲击射流转变所致。由此得到,调节阀在中小升程下存在数值模拟的流型不确定区,该区域中即使是同一工况下也会出现2种流型,通过声音突变现象可以确定这一区域,这是一种简单且实用的验证数值模拟流型分布范围的方法。本文对阀内流型的揭示和依靠声音突变方法来判断流型,对于数值模拟调节阀内的流动具有实际意义。

[1] 王平子. 一种工作可靠阻力低的汽轮机卸载调节阀 [J]. 东方电气评论, 1996(2): 73-79. WANG Pingzi. A turbine unload valve with reliable and low resistance [J]. Dongfang Electric Review, 1996(2): 73-79.

[2] 胡剑, 张宝. 国产600 MW汽轮机调节汽门阀杆脱落原因分析 [J]. 浙江电力, 2009, 28(3): 45-47. HU Jian, ZHANG Bao. Cause analysis for governing valve level fall-off in 600 MW steam turbine [J]. Zhe-jiang Electric Power, 2009, 28(3): 45-47.

[3] 张奇, 徐义巍. 捷制500 MW汽轮机组高压调气门门杆断裂的原因分析及改进 [J]. 山西电力, 2002(5): 51-52. ZHANG Qi, XU Yiwei. The analysis and improvement of Czech control valve’s steam fracture for 500 MW high pressure steam turbine [J]. Shanxi Electric Power, 2002(5): 51-52.

[4] HEYMANN F J, STAIANO M A. Steam turbine control valve noise [J]. The Journal of the Acoustical Society of America, 1973, 54(1): 289-301.

[5] ARAKI T, OKAMOTO Y, OOTOMO F. Fluid induced vibration of steam control valves [J]. Toshiba Review, 1981, 36(7): 0372-0462.

[6] TECZA J, CHOCHUA G, MOLL R. Analysis of fluid-structure interaction in a steam turbine throttle valve, GT2010-23788 [R]New York, USA: ASME, 2010.

[7] CLARI M B, POLKLAS T, JOOS F. Three-dimensional flow separations in the diffuser of a steam turbine control valve, GT2011-45617 [R]. New York, USA: ASME, 2011.

[8] HARDIN J, KUSHNER F, KOESTER S. Elimination of flow-induced instability from steam turbine control valves [C]∥Proceedings of the 32nd Turbomachinery Symposium. Williams Building, TX, USA: Texas A&M University, 2003: 99-108.

[9] ZHANG D, ENGEDA A. Venturi valves for steam turbines and improved design considerations [J]. Proceedings of the Institution of Mechanical Engineers: Part A Journal of Power and Energy, 2003, 217(2): 219-230.

[10]MORITA R, INADA F, MORI M, et al. CFD simulations and experiments of flow fluctuations around a steam control valve [J]. Journal of Fluids Engineering, 2007, 129(1): 48-54.

[11]YONEZAWA K, OGAWA R, OGI K, et al. Flow-induced vibration of a steam control valve [J]. Journal of Fluids and Structures, 2012, 35(9): 76-88.

[12]SPALART P, JOU W, STRELETS M, et al. Comments of feasibility of LES for wings, and on a hybrid {RANS/LES} approach [J]. Journal of Advances in DNS/LES, 1997, 1(1): 4-8.

[13]STRELETS M. Detached eddy simulation of massively separated flows, 2001-0879 [R]. Reston, USA: AIAA, 2001.

[14]HOFFMANN K A, CUMMINGS R M, SQUIRES K D. Detached-eddy simulation with compressibility corrections applied to a supersonic axisymmetric base flow [J]. Journal of Fluids Engineering, 2002, 124(2): 911-923.

[15]SPALART P. Strategies for turbulence modelling and simulations [J]. International Journal of Heat and Fluid Flow, 2000, 21(3): 252-263.

[16]PLUVIOSE M. Stabilization of flow through steam-turbine control valves [J]. ASME Journal of Engineering for Gas Turbines and Power, 1989, 111(4): 642-646.

[17]JURY F D. Fundamentals of aerodynamic noise in control valves [M]∥ Fisher Controls International Inc. Technical Monographs. Marshaltown, IA, USA: Fisher Control International Inc., 1999: 1-24.

[18]SINGLETON E. The impact of IEC 534-8-3 on control valve aerodynamic noise prediction [J]. Measurement and Control, 1999, 32(2): 37-44.

[19]CHOW G, REETHOF G. A study of valve noise gen-

eration processes for compressible fluids, 80-WA/NC-15 [R]. New York, USA: ASME, 1980.

[20]REETHOF G, WARD W. A theoretically based valve noise prediction method for compressible fluids [J]. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1986, 108(3): 329-338.

[21]刘利杰. 某调节阀的气动噪声研究 [D]. 哈尔滨: 哈尔滨工程大学, 2013.

[22]邓达泰. 汽轮机调节阀内气动噪声特性和基于流场优化的控制方法探究 [D]. 西安: 西安交通大学, 2011.

[23]ZHANG D, ENGEDA A, HARDIN J, et al. Experimental study of steam turbine control valves [J]. Proceedings of the Institution of Mechanical Engineers: Part C Journal of Mechanical Engineering Science, 2004, 218(5): 493-507.

(编辑 苗凌)

Distribution of Flow Pattern in Control Valves and Identification of Flow Pattern Transition by Sound Mutation

ZENG Lifei1, LIU Guanwei1, MAO Jingru1, YUAN Qi1, WANG Zhaoyang1, WEI Long1, ZHANG Junjie2, XU Yatao2

(1. Institute of Turbomachinery, Xi’an Jiaotong University, Xi’an 710049, China; 2. Shenhua Guohua (Beijing) Electric Power Research Institute Co., Ltd., Beijing 100025, China)

Flow-induced vibration and noise of control valves are experimentally and numerically studied to further investigate the relationships between flow pattern distribution, and vibration noise in a steam turbine. It is found that there exist two flow patterns in small and middle openings. Compared with core flow pattern, the flow pattern attached to the valve seat gets more stable with less noise. Different flow patterns may appear even under the same condition according to different adjustment methods of pressure ratios. A sound mutation caused by the converting of two different flow patterns is experimentally observed by continuously adjusting the pressure ratio, which can be used as a simple and practical way to determine the ranges of core and the annular flows.

control valve; flow pattern; vibration; numerical simulation

2014-09-21。

曾立飞(1986—),男,博士生;毛靖儒(通信作者),女,研究员。

时间:2015-02-27

10.7652/xjtuxb201505018

TK263.7

A

0253-987X(2015)05-0116-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150227.0845.007.html