基于静载试验的既有石拱桥技术状态评定

陈俊，张宇胜，苏永华

(1.山西省吉河高速公路建设管理处，山西临汾041000;2.中国铁道科学研究院铁道建筑研究所，北京100081)

基于静载试验的既有石拱桥技术状态评定

陈俊1，张宇胜2，苏永华2

(1.山西省吉河高速公路建设管理处，山西临汾041000;2.中国铁道科学研究院铁道建筑研究所，北京100081)

修建于上世纪的石拱桥大部分已经进入超期服役阶段，其技术状态直接影响车辆通行安全，而结构参数的变异性以及结构响应理论值的不确定性给桥梁评定造成一定困难。本文以一座石拱桥为试验对象，提出了一套适用于既有石拱桥技术状态的评定方法。该方法融合了外观调查、静载试验两者的优势，通过分析施加荷载与结构响应的关联程度推断桥梁的承载能力。

石拱桥 技术状态 静载试验 承载力 外观调查

20世纪50—60年代，我国在公路中修建了大量的石拱桥。随着时间的推移，自然侵蚀作用使得这些石拱桥出现表面风化、材料强度降低等现象，加之养护不当，结构病害不断出现。另一方面，经济、社会发展使桥上交通流量、载重不断增加。因此，石拱桥不断下降的承载能力与日益增长的交通需求之间矛盾越来越大。如何快速有效地评定这些石拱桥的技术状态，成为目前研究的热点［1-3］。

外观调查、静载试验是桥梁技术状态评定最为常用的两种方法［4-5］。外观调查只能掌握桥梁病害程度，无法实现定量评价。静载试验通过在桥梁指定位置施加静荷载，测试关键截面的应变、挠度等参数，将测试结果与理论值进行对比，可以评价结构的承载能力。

目前在役的石拱桥自身材料性能与成桥之初相比已经发生很大变化，很难精确确定。另一方面，采用有限元模型又难以精确模拟既有石拱桥的受力状态［6］。

本文以某石拱桥为背景，提出了一套适用于既有石拱桥技术状态的评定方法。首先，调查桥梁设计、施工以及维修养护资料;其次，对桥梁进行检查和检测，掌握桥梁的整体技术状况和病害程度;然后，综合拱桥受力特点及病害检查结果，确定静载试验加载图式，布置测点，测试结构在荷载下的响应，分析响应与荷载的关联程度;最后，综合评价桥梁的耐久性以及承载能力。

1 桥梁概况

该桥为一座3孔石拱桥，全长115 m，每孔净跨为30 m，矢高6.6 m，每孔主拱上设6个跨度2.5 m的腹拱;桥面行车道宽9.0 m，两侧各设宽1.5 m人行道;桥下部结构为重力式墩台。桥梁采用“土牛拱胎”方法施工，于1959年5月建成。桥梁设计规范采用1956年版《中华人民共和国公路工程设计准则》，设计活载为汽—10。桥梁经过数次大修，但维修资料缺失。截至2012年，桥梁已超过原设计寿命3年，通行荷载已超过最初设计，且呈现不断增大的趋势。因此，评定桥梁的技术状态，确保桥梁结构运营安全，具有重要的经济价值和社会意义。

2 外观调查

桥面系涉及栏杆、人行道、行车道、伸缩缝等部分，典型病害为混凝土开裂、路缘石混凝土缺失、铺装层凸凹不平、伸缩缝堵塞。

拱上结构主要涉及立墙、腹拱等部分。除表面发生了一定风化外，立墙基本完好。腹拱表面严重风化，砂浆缺失，表面渗水并且出现白色结晶物。

主拱圈基本完好，无明显竖向变形，未发现石块断裂、脱落等异常现象。拱圈部分灰缝松散脱落，存在大范围风化现象，多处明显渗水，并伴有晶体析出。中孔跨中截面下游侧靠近泄水孔处存在两条明显的纵向裂缝，一条裂缝宽0.3 mm、长3.0 m，另外一条裂缝宽0.5 mm、长12.0 m。拱脚完好，未发现明显位移。

中孔跨中主拱圈存在的两条纵向裂缝属于主要构件上的较大缺损，对结构承载能力有着严重影响。因此，大桥总体技术状况等级评定为4类［5］。

3 静载试验

3.1 试验方案

选定清凉山侧边孔及中孔作为试验孔，测试截面选取如图1所示。

具体测试项目如下:

1)结构最大挠度，包括C—C截面(边孔L/4截面)、D—D截面(边孔L/2截面)、E—E截面(边孔3L/4截面)、I—I截面(中孔L/4截面)、J—J截面(中孔L/2截面)。

2)结构控制截面局部相对变形，包括B—B截面(边孔拱脚截面)、C—C截面、D—D截面、E—E截面、F—F截面(边孔拱脚截面)、H—H截面(中孔拱脚截面)、I—I截面、J—J截面。

图1 桥梁静载试验截面

3)墩台沉降与拱脚水平位移，包括A—A截面、G—G截面、K—K截面。

在所有局部相对变形测试截面的下表面沿桥梁横向均匀布置3只振弦式应变计。由于石料强度、弹性模量远大于砂浆，相同荷载作用下其变形要比砂浆小得多。应变计跨砂浆缝布置，在砂浆缝表面部分缺失的情况下，所测应变值反映的是结构局部相对变形而非材料本身的应变。

在所有L/2挠度测试截面的下表面沿着桥梁横向均匀布置3只挠度计。在所有L/4，3L/4挠度测试截面的下表面桥梁中线处布置1只位移计。在每个墩台测试截面布置竖向、水平位移计2只。

鉴于桥梁实际通行荷载接近城A标准，实际试验加载效应在汽—10与城A标准之间。试验采用3辆单车总重300 kN工程车(前轴距3.5 m，后轴距1.3 m)加载，如图2所示。

图2 加载车辆布置(单位:m)

B—B，H—H截面加载控制面均距截面5 m。两截面荷载施加分为三级，每级增加对应编号的车辆，实际最大加载负弯矩为1 631 kN·m，为城A标准的0.89倍。

F—F截面加载控制面距截面5 m(清凉山方向)。该截面荷载施加一级到位;实际最大加载负弯矩为1 710 kN·m，为城A标准的0.93倍。

C—C，I—I截面荷载施加均分为三级，每级增加对应编号的车辆，实际最大加载正弯矩为1 027 kN·m，为城A标准的0.80倍。

E—E截面荷载施加一级到位，实际最大加载正弯矩为962 kN·m，为城A标准的0.75倍。

D—D，J—J截面荷载施加均分为三级，每级增加对应编号的车辆;实际最大加载弯矩为826 kN·m，为城A标准的0.71倍。

3.2 试验结果

3.2.1 变形分析

将相同布置条件下实际加载车辆与一辆30 t标准车(前轴60 kN、双轴240 kN)产生的理论挠度之比定义为挠度加载系数。图3给出C—C截面挠度随着挠度加载系数的变化曲线。其中，线性预测值是指依据第一级加载结果和挠度加载系数线性外推得到第二、三级加载的预测挠度值。从图3可以看出:随着挠度加载系数的增大，实测结果与线性预测值之间的差值变大。C—C截面最大挠度为1.31 mm，最大残余挠度为0.07 mm，相对残余变形为5%。

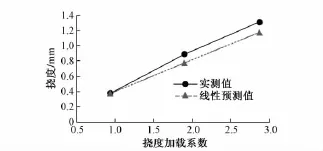
图3 C—C截面挠度与挠度加载系数关系

E—E截面在最大试验荷载作用下的最大挠度为1.66 mm，最大残余挠度为0.07 mm，相对残余变形为4%。

表1给出了各级加载时D—D截面的挠度变化情况。其中，测点1，2，3分别布置于上游侧、桥梁中线处、下游侧。D—D截面最大相对残余变形为8%。

图4、图5分别给出了D—D截面测点2的挠度、平均挠度值与挠度加载系数的关系曲线。

表1 D—D截面挠度变化mm

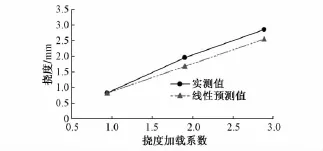
图4 D—D截面测点2的挠度与挠度加载系数关系

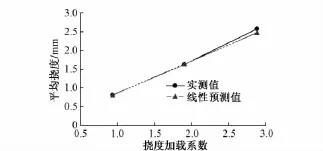
图5 D—D截面平均挠度与挠度加载系数关系

实测结果表明，D—D截面挠度实测值与线性预测值差异随着挠度加载系数的增大而增大。

表2给出了各级加载时J—J截面的挠度变化情况。从中可以看出，J—J截面在加载结束之后的相对残余变形较小，最大为9%。

表2 J—J截面挠度变化mm

图6、图7分别给出了J—J截面测点2的挠度、平均挠度值与挠度加载系数的关系曲线。

从图6、图7可以看出:J—J截面中线挠度的实测值与线性预测值差异随着挠度加载系数的增大而增大，而J—J截面挠度的实测均值与线性预测结果基本一致。值得注意的是，在各级荷载作用下测点3的挠度均明显小于测点1、测点2。这可能是测点2，3之间存在的纵向裂缝降低了J—J截面横向整体性能所致。

图8给出I—I截面挠度随着挠度加载系数的变化曲线。从中可以看出:I—I截面中线挠度的实测值与线性预测值差异随着挠度加载系数的增大而增大。I—I截面最大挠度为1.46 mm，最大残余挠度为0.02 mm，相对残余变形为1%。

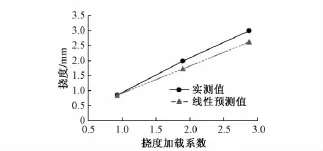
图6 J—J截面测点2的挠度与挠度加载系数关系

图7 J—J截面平均挠度与挠度加载系数关系

图8 I—I截面挠度与挠度加载系数关系

在各个工况下，A—A，G—G，K—K截面的水平、竖向变位数值极小，可以认为拱脚稳定。

3.2.2 应变测试结果分析

表3给出了各级荷载作用下B—B截面应变实测值。其中，S1，S2，S3分别对应上游侧、桥梁中线、下游侧。从表3可以看出，B—B截面的相对残余应变为10%。

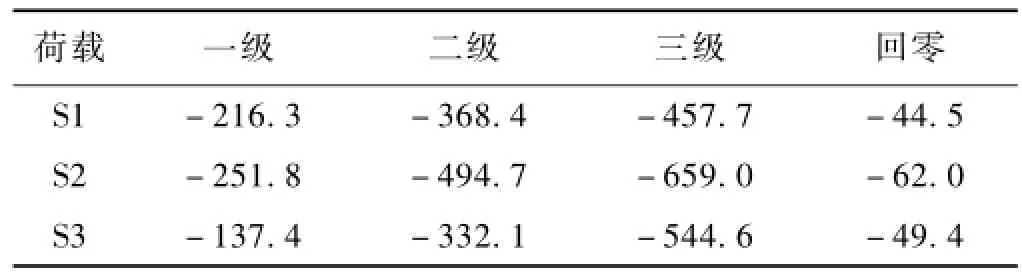
表3 B—B截面应变实测值10-6

图9给出了B—B截面测点实测应变值与加载车数量的关系曲线。从中不难看出，B—B截面的局部相对应变随着加载车数量的增加近似呈线性增大。

图9 B—B截面应变实测值与加载车数量关系

表4给出了各级荷载作用下C—C截面应变实测值。从中不难看出，C—C截面的相对残余应变为8%。

表4 C—C截面应变实测值10-6

图10给出了C—C截面各测点实测应变值与加载车数量的关系。不难看出C—C截面的局部应变随着加载车辆的增加近似呈线性增大。

图10 C—C截面应变实测值与加载车关系

表5给出了各级荷载作用下D—D截面应变实测值。从中不难看出，D—D截面的相对残余应变为10%。

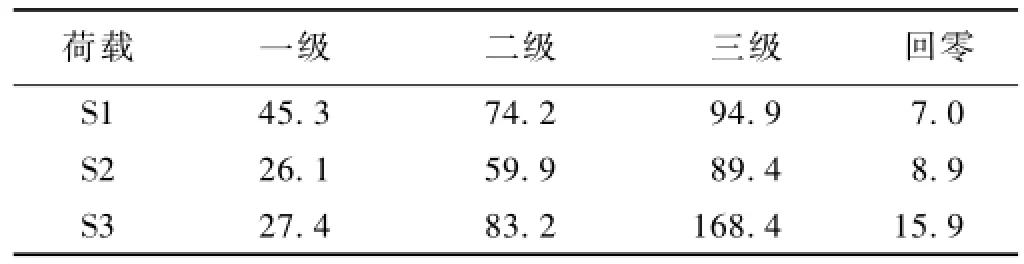
表5 D—D截面应变实测值10-6

图11给出了D—D截面各测点实测应变值与加载车数量的关系曲线。从中不难看出，D—D截面的局部相对变形随着加载车数量的增加近似呈线性增大。

图11 D—D截面应变实测值与加载车关系

表6给出了E—E，F—F，H—H截面各个测点的实测应变值。从中可以看出，E—E，F—F，H—H截面各个测点的相对残余应变较小，最大分别为6%，5%，10%。

表6 三截面应变实测值10-6

表7给出了各级荷载作用下I—I截面实测应变值，可见各个测点的相对残余应变较小，最大为3%。图12给出了I—I截面各测点实测应变值与加载车数量的关系，可见截面的局部相对变形随着加载车辆的增加近似呈线性增大。

表7 I—I截面应变实测值10-6

图12 I—I截面应变实测值与加载车关系

表8给出了各级荷载作用下J—J截面各测点的实测应变值，可见各个测点的相对残余应变较小，最大为5%。图13给出了J—J截面实测应变值与加载车数量的关系。从中不难看出，J—J截面的局部相对应变随着加载车辆的增加近似呈线性增大。

表8 J—J截面应变计实测值10-6

图13 J—J截面应变实测值与加载车关系

3.3 结构承载能力评估

1)试验荷载作用下桥梁墩台变位极小，状态比较稳定。

2)各测试截面挠度实测值与预测值的差异随挠度加载系数的增大而增大。

3)各测试截面局部相对应变与加载车数量大致成线性关系，相对残余应变较小。

综上，本石拱桥承载能力评定结果表明，整体受力在试验荷载作用下基本处于弹性工作状态，满足原汽—10设计要求，但不能满足城A标准要求。中孔跨中主拱圈纵向开裂后导致整体受力性能显著降低。

4 结论

1)本石拱桥的承载能力不能满足目前通行要求，需要对车辆进行限载，允许通过车辆的单车总重不应超过150 kN。

2)主拱圈是石拱桥的主要承重构件，纵向开裂后导致结构整体承载力出现下降，需采取措施进行加固处理。

目前我国公路老龄石拱桥数量较多，部分桥梁的技术状态不明确，运营安全存在不确定性。本文通过静载试验评定既有石拱桥技术状态的方法可以为类似桥梁的技术评定提供参考。

［1］徐圣祥.既有圬工拱桥检测和评定方法研究［D］.成都:西南交通大学，2010.

［2］蔡斌.服役石拱桥加固技术研究［D］.长沙:中南大学，2010.

［3］刁砚，钱永久，王振领.填芯法加固双曲拱桥的有限元分析及运用［J］.铁道建筑，2010(7):30-32.

［4］中华人民共和国交通运输部.JTG/T J21—2011公路桥梁承载能力检测评定规程［S］.北京:人民交通出版社，2011.

［5］中华人民共和国交通运输部.JTG/T H21—2011公路桥梁技术状况评定标准［S］.北京:人民交通出版社，2011.

［6］聂建国，樊健生.700年石拱桥的静力加载试验与结构分析［J］.清华大学学报，2003，43(6):840-843.

Assessment on technical state of existing stone arch bridge based on static loading test

CHEN Jun1，ZHANG Yusheng2，SU Yonghua2
(1.Jihe Highway Construction Management Department of Shanxi Province，Linfen Shanxi 041000，China; 2.Railway Engineering Research Institute，China Academy of Railway Sciences，Beijing 100081，China)

Stone arch bridge built last century has been used longer than their designed service life，and the problem of operation safety shall be noticed.It is difficult to evaluate the bridge since the variability of structure parameter and the uncertainty of structure response.In this paper，a stone arch bridge was studied.An approach was proposed for evaluation of existing stone arch bridges.T he method has the advantage of both observation and static load testing. T he bearing capacity of the bridge may be assessed through the relationship between the load and the structural response.

Stone arch bridge;T echnical state;Static loading test;Bearing capacity;Observation

U448.3

A

10.3969/j.issn.1003-1995.2015.02.05

1003-1995(2015)02-0016-05

(责任审编孟庆伶)

2014-06-05;

2014-09-20

陈俊(1967—)，男，山西襄汾人，高级工程师。