基于模糊超球面SVM的雷达高分辨距离像识别*

史朝辉,王　坚,华继学

(空军工程大学防空反导学院,西安　710051)

基于模糊超球面SVM的雷达高分辨距离像识别*

史朝辉,王坚,华继学

(空军工程大学防空反导学院,西安710051)

摘要:高分辨距离像(HRRP)分类是对雷达复杂目标分类的一种重要方法。标准的一对一超球面SVM多值分类方法需要训练k(k-1)个子分类器,计算量大、训练时间长,并且存在决策盲区,不适宜用来进行HRRP目标识别。为了减少分类器数量,提高训练速度,文中根据超球面的几何特征引入了一种“倒数对称”的一维隶属度,构造了模糊超球面SVM分类器,该方法仅需训练k(k-1)/2个子分类器,既提高了训练速度又解决了决策盲区,HRRP实测数据识别实验表明了该方法的有效性。

关键词:超球面支持向量机;高分辨距离像;隶属度

0引言

雷达目标高分辨一维距离像(high range resolution profile, HRRP)为物理特征相似的复杂目标分类、识别提供了必要的信息来源[1]。由于环境、目标的复杂性、目标的伪装及反雷达能力、目标运动的非合作性等因素的存在,要获得目标各种角度各个姿态的HRRP几乎是不可能的,即使获得,样本数据量也是有限的。因此,基于HRRP的目标识别通常是一个典型的高维数、小样本问题[2]。

支持向量机(support vector machine, SVM)是在统计学习理论基础上发展起来的一种新的模式识别方法。用SVM对HRRP进行目标识别取得了较好的效果[3-5]。超球面SVM算法[6-7]是为解决奇异点单值分类问题而生的,文献[8-9]对超球面SVM算法的多值分类问题进行了研究,给出了一对一超球面SVM多值分类方法。然而标准的一对一超球面SVM多值分类方法需要训练k(k-1)个子分类器,计算量大,训练时间长,不适宜用来进行HRRP目标识别。为减少分类器数量,文中给出了隶属度“倒数对称”法,该方法仅需训练k(k-1)/2个子分类器,既保证了训练精度又提高了训练速度,HRRP实测数据识别实验表明了该方法的有效性。

1一对一超球面SVM多值分类器

在超球面SVM中,给出了一个二值决策函数,可以对该决策函数进行修改,去掉表达式中的符号函数,将决策函数作为实值函数,即取:

(1)

对于测试样本x,将产生k(k-1)个输出:fij(x),i,j=1,2,…,k,i≠j,将实值决策函数fij(x),i,j=1,2,…,k,i≠j作为一维隶属度函数。

定义样本x属于第i类的隶属函数为:

(2)

样本x按如下原则进行分类:

(3)

由于超球面分类不像超平面那样对参与分类的两类是反对称的(即fij=-fji),采用实值函数模糊判决,一对一超球面SVM多值分类方法需要训练k(k-1)个子分类器。

2隶属度“倒数对称”法

在组合k(k-1)个判定结果时,可考虑直接将测试样本距各超球球心距离的倒数作为一维隶属度函数进行决策。

定义样本x属于第i类的隶属函数为:

(4)

式中:cij为以第i类为正类,第j类为负类训练而成的超球的球心;D(x,cij)为样本x到球心cij的映射空间中的距离。

样本x按如下原则进行分类:

(5)

式(4)是对绝对距离的比较,另一方面可以同时考虑各个超球半径的影响,比较相对距离,即定义:

(6)

易证式(2)和式(3)组成的决策方法同式(6)和式(5)组成的决策方法是等价的。式(4)和式(5)采用绝对距离,其可靠性得不到保证,不宜采用。

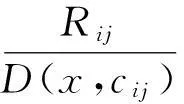
对称”法。

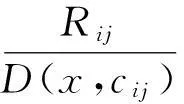
(7)

式中Inf表示无穷大。

分类决策方式如下:

样本x属于第i类的隶属函数为:

(8)

样本x按如下原则进行分类:

(9)

引入“倒数对称”一维隶属度,模糊一对一超球面SVM分类器只需训练k(k-1)/2子分类器,可成倍提高训练速度。

3实验结果与分析

为验证算法在HRRP识别中的有效性,使用某型雷达测得的J600、F1601、F1700、FY200、B200等5种类型飞机的高分辨一维距离实测数据进行实验。原始数据经反傅里叶变换得到各目标0°~180°角范围内,角度间隔为0.5°的128维HRRP数据,取0°~30°角的一组数据,样本数300,如图1~图5所示。

HRRP分类实验分5次进行,每次随机抽取2/3作为训练样本,其余1/3作为测试样本,分类结果取5次结果的平均值。

采用一对一超球面SVM多类分类,对实值决策函数与隶属度“倒数对称”两种模糊判决方法作对比实验。核函数均用径向基函数,惩罚参数C=1 000。表1给出了两种方法平均训练时间的对比结果。表2给出了实值决策函数模糊判决法与隶属度“倒数对称”法分类正确率的对比。

从实验结果可看出隶属度“倒数对称”法使得训练速度显著提高,且分类性能总体上要优于实值决策函数模糊判决法。

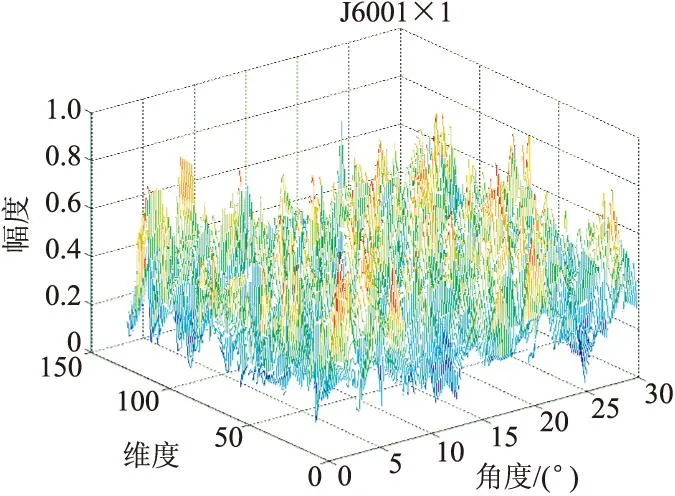
图1　J600目标0°~30°角HRRP数据

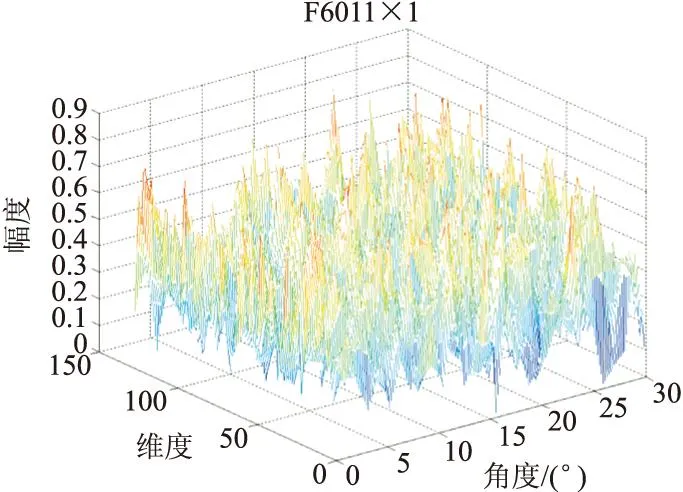
图2　F1601目标0°~30°角HRRP数据

图3　F1700目标0°~30°角HRRP数据

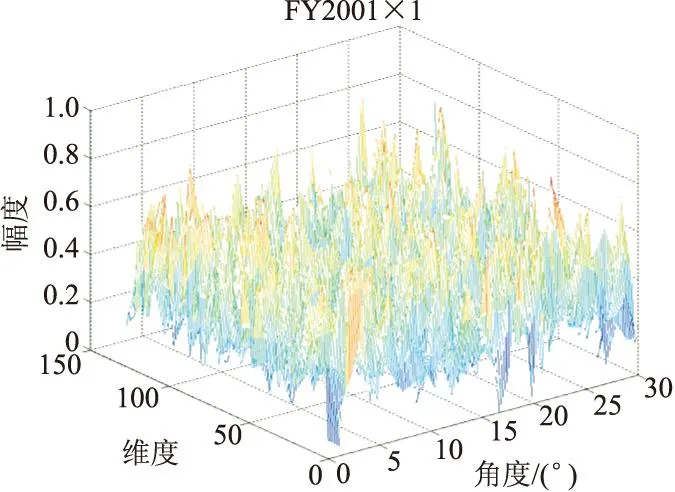
图4　FY200目标0°~30°角HRRP数据

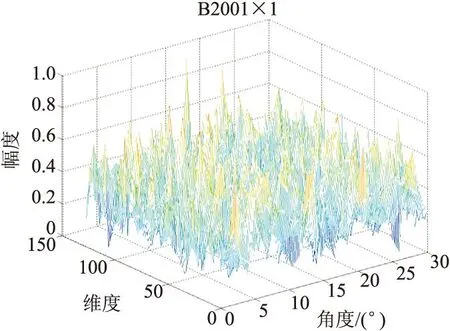
图5　B200目标0°~30°角HRRP数据

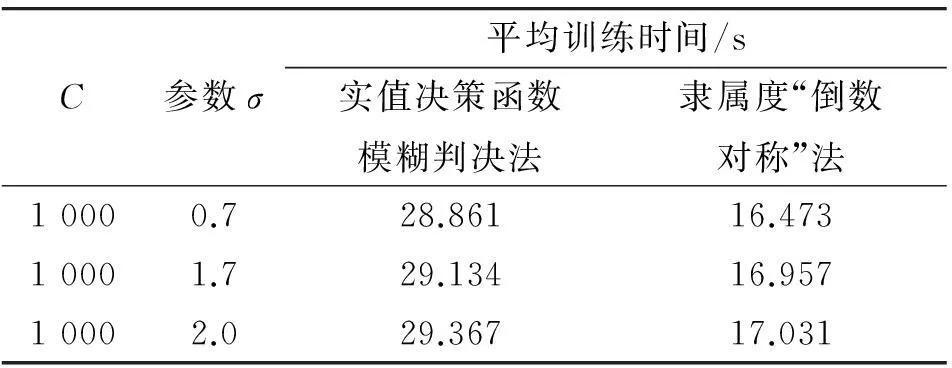
C参数σ平均训练时间/s实值决策函数模糊判决法隶属度“倒数对称”法10000.728.86116.47310001.729.13416.95710002.029.36717.031

表2　HRRP分类正确率比较

4结束语

为了将模糊一对一超球面SVM多值分类器应用于雷达高分辨距离像识别,文中给出了一种新的隶属度设定方法——“倒数对称”法,该方法仅需训练k(k-1)/2个子分类器,提高了训练速度,HRRP分类实验验证了该方法对HRRP识别的有效性。

参考文献:

[1]Hudson S, Psaltis D. Correlation filters for aircraft identification from radar range profles [J]. IEEE Trans. on AES, 1993, 29(3): 741-748.

[2]王晓丹. 高分辨雷达目标识别中的若干问题研究 [R]. 西安: 空军工程大学导弹学院, 2003.

[3]李莹, 任勇, 山秀明. 基于支持向量机的高分辨距离像分类法 [J]. 系统工程与电子技术, 2002, 24(11): 8-10.

[4]沈丽民, 李军显. 基于支持向量机的雷达高分辨距离像识别 [J]. 弹箭与制导学报, 2009, 29(2): 231-234.

[5]李志鹏, 马田香, 杜兰, 等. 在雷达HRRP识别中多特征融合多类分类器设计 [J]. 西安电子科技大学学报: 自然科学版, 2013, 40(1): 111-117.

[6]Tax D, Duin R. Data domain description by support vectors [C]∥Proceedings of ESANN99, 1999: 251-256.

[7]Schölkopf B, Burges C J C, Vapnik V. Extracting support data for a given task [C]∥Fayyad U M, Uthurusamy R, eds. Proceedings of First International Conference on Knowledge Discovery & Data Mining. German: AAAI Press, 1995: 262-267.

[8]Hsu Chih-Wei, Lin Chih-Jen. A comparison of methods for multi-class support vector machines [J]. IEEE Transactions on Neural Networks, 2002, 13(2): 415-425.

[9]史朝辉. SVM算法研究及在HRRP分类中的应用 [D]. 西安: 空军工程大学, 2005.

收稿日期:2014-03-30

基金项目:国家自然科学基金(61273275)资助

作者简介:史朝辉(1974-),男,河北博野人,博士研究生,研究方向:智能信息处理,模式识别,支持向量机研究。

中图分类号:TN957

文献标志码:A

Radar High Range Resolution Profile Identification Based on
Fuzzy Hypersphere SVM

SHI Zhaohui,WANG Jian,HUA Jixue

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

Abstract:High resolution range profile (HRRP) classification is an important method for radar complex target classification. Since standard one-against-one hypersphere support vector machine (SVM) has the defects of large computation, long training time for its k(k-1) sub-classifiers, and, decision bland area, it is not fit for HRRP target recognition. In order to reduce the number of classifiers in the one-against-one multi-class, a new one-dimensional membership function based on geometry feature named “reciprocal symmetry “ has been defined, and the corresponding fuzzy hypersphere SVM has been given. This new method only needs k(k-1)/2 sub-classifiers, it not only improves the training speed, but also clears away the decision bland area. The HRRP real data experimental results show that this algorithm has better HRRP classification performance.

Keywords:hypersphere SVM; high resolution range profile; membership function