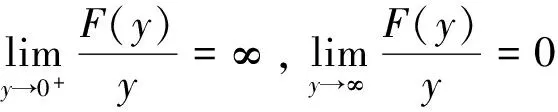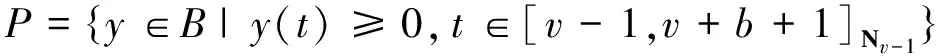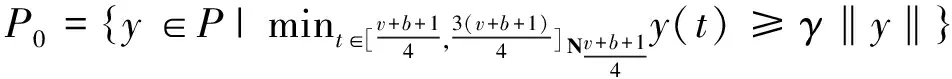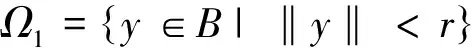带有分数阶边值条件的分数阶差分方程的正解
2015-12-26郭成丁卯松韩筱爽
郭成, 丁卯松, 韩筱爽
( 延边大学 科学技术学院, 吉林 延吉 133002 )
带有分数阶边值条件的分数阶差分方程的正解
郭成, 丁卯松, 韩筱爽*
( 延边大学 科学技术学院, 吉林 延吉 133002 )
研究了一类带有分数阶边值条件的分数阶差分方程正解的存在性问题.首先利用分数阶差分方程理论和边值条件给出了解的结构,其次分析了Green函数的一些性质,最后利用锥上的不动点定理证明了该问题正解的存在性.
分数阶边值条件; Green函数; 正解
0 引言
分数阶微积分广泛应用于信号处理与控制、流体力学、分形理论、分数阶PID控制器设计等科学研究领域.近年来随着分数阶差分方程模型的不断出现,以及对微分方程近似计算的需要,分数阶差分方程边值问题逐渐成为学者们关注的研究课题.分数阶差分方程的边值条件种类很多,如带有两点边值条件[1]、局部边值条件[2]和非局部边值条件[3]的分数阶差分方程,其中即使边值条件带有差分方程结构也大多是整数阶次.文献[4]研究了带有分数阶边值条件的差分方程,对其边值条件进行分析,并把它归结为非局部类型.本文在前人的研究基础上,讨论了方程格林函数的一些性质,并利用锥上的不动点定理证明了该边值问题存在正解.
考虑如下带有分数阶边值条件的分数阶差分方程的边值问题:
(1)
1 预备知识[5-9]
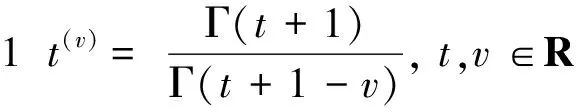
引理1 对于∀t,v∈R, 如果t(v),t(v-1)都有定义,则有Δt(v)=v t(v-1).
定义2 对于v>0, 函数f的分数阶(v阶)和分定义为

定义3 对于N∈N, 0≤N-1 Δvf(t)=ΔNΔv-Nf(t), t∈Na+N-v. 引理2 设f是定义在Na上的实函数, μ,v>0, 则有 Δ-v(Δ-μf(t))=Δ-(v+μ)f(t)=Δ-μ(Δ-vf(t)), t∈Na+μ+v. 引理3 令0≤N-1 ① ‖Ty‖≤‖y‖, y∈P∩∂Ω1, ‖Ty‖≥‖y‖, y∈P∩∂Ω2; ② ‖Ty‖≥‖y‖, y∈P∩∂Ω1, ‖Ty‖≤‖y‖, y∈P∩∂Ω2, 定理1[4]设h∶[v-1,v+b]Nv-1×R→R, 则问题 (2) 是问题(2)的格林函数.这里 T1={(t,s)∈[v-2,v+b+1]Nv-2×[0,b+1]N0: 0≤s T2={(t,s)∈[v-2,v+b+1]Nv-2×[0,b+1]N0: 0≤t-v+1 定理2 Green函数G(t,s)具有以下性质: (I) G(t,s)>0, (t,s)∈[v-2,v+b+1]Nv-1×[0,b+1]N0; (II) maxt∈[v-2,v+b+1]Nv-1G(t,s)=G(s+v-1,s), 其中s∈[0,b+1]N0; (III) 存在γ∈(0,1), 使得mint∈TG(t,s)≥γmaxt∈[v-1,v+b+1]Nv-1G(t,s)=γ G(s+v-1,s). 即G(t,s)>0.综上,结论(I)成立. 则有ΔtG(t,s)<0, 即G(t,s)≤G(s+v-1,s).综上,结论(II)成立. (H1) f(t,y)≥0且连续; 定义B上的锥 引理5 假设条件(H1)成立,则对于∀y∈P有Ty∈P0.特别地,算子T是锥P0到P0上的映射. 定理3 (I)如果条件(H1)和(H2)成立,则问题(1)至少有一个非零解y∈P0; (II) 如果条件(H1)和(H3)成立,则问题(1)至少有一个非零解y∈P0. [1] Atici F M, Eloe P W. Two-point boundary value problems for finite fractional difference equations[J]. J Difference Equ Appl, 2011,17(4):445-456. [2] Goodrich C S. Solutions to a discrete right-focal boundary value problem[J]. Int J Difference Equ, 2010,5:195-216. [3] Goodrich C S. Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions[J]. J Comput Math Appl, 2011,61(21):191-202. [4] Goodrich C S. On a fractional boundary value problem with fractional boundary conditions[J] . J Applied Mathematics Letters, 2012,25:1101-1105. [5] Miller K S, Ross B. Fractional difference calculus, procedings of the internations symposium on Univalent functions[J]. Fractional Calculus and their Applications Nihon University, 1988,1(4):139-152. [6] Atici F M, Eloe P W. A transform method in discrete fractional calculus[J]. Int J Difference Equ, 2007,2(2):165-176. [7] Atici F M, Eloe P W. Initial value problems in discrete fractional calculus[J].Proc Amer Math Soc, 2009,137:981-989. [8] 时宝,张德存,盖久明.微分方程理论及其应用[M] .北京:国防工业出版社,2005:13. [9] 程金发.分数阶差分方程理论[M].厦门:厦门大学出版社,2010. Existence of positive solution for a fractional difference equations with fractional boundary value condition GUO Cheng, DING Maosong, HAN Xiaoshuang* (InstituteofScienceandTechnology,YanbianUniversity,Yanji133002,China) We study the existence of positive solutions of the boundary value problem for a fractional difference equation with fractional boundary value condition. Firstly, according to the theory of fractional difference equation and its boundary conditions, we got the structure of solutions, then analyze some properties of the Green’s function, at last, the existence of the positive solutions of the problem is proved by using the fixed point theorem in cones. fractional order boundary value condition; Green’s function; positive solution 2014-09-21 基金项目: 延边大学自然科学基金资助项目(延大科合字2013第11号) 1004-4353(2015)01-0025-05 O175.6 A *通信作者: 韩筱爽(1980—),女,讲师,研究方向为可靠性与微分方程理论.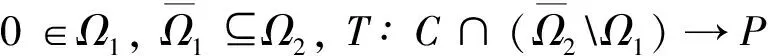
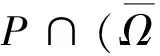
2 Green函数及其性质




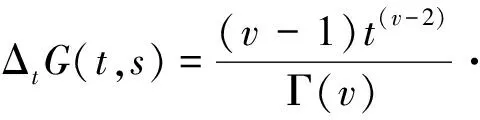
3 正解的存在性