基于EEMD降噪与非抽样提升小波包的滚动轴承故障诊断方法

肖顺根， 宋萌萌， 孔庆光， 陈肇祥

( 宁德师范学院 物理与电气工程系， 宁德 352100 )

基于EEMD降噪与非抽样提升小波包的滚动轴承故障诊断方法

肖顺根， 宋萌萌， 孔庆光， 陈肇祥

( 宁德师范学院 物理与电气工程系， 宁德 352100 )

针对传统小波包在诊断滚动轴承隐含故障中存在频率混叠、精度不高等问题，提出一种基于集成经验模态分解(ensemble empirical mode decomposition，EEMD)降噪与非抽样提升小波包相融合的故障诊断方法.首先利用EEMD方法分解原始故障信号得到多个本征模态函数(intrinsic mode function,IMF)分量，然后计算各个IMF分量与原始信号间的相关系数，并与设置的相关系数阈值相比较，将小于阈值的IMF分量视为伪分量予以剔除；对剩余的IMF分量采用峭度准则再次筛选最优IMF分量进行重构，进而实现降噪目的.为了避免传统小波包因采取抽样运算方式导致频率混叠情况，文中采用非抽样运算的提升小波包来分解降噪信号，并采用Hilbert变换进行包络解调分析得到滚动轴承的故障位置.仿真实验和滚动轴承内圈故障应用实例表明：采用EEMD分解原始故障信号，结合相关系数-峭度准则，达到了很好的降噪效果；采用非抽样提升小波包比传统小波包具有更高的故障诊断精度，且不存在频率混叠问题.

滚动轴承； EEMD； 相关系数-峭度准则； 频率混叠； 非抽样提升小波包

滚动轴承是旋转机械系统中非常重要的零部件，也是容易损伤的零部件，其工作性能的好坏直接影响着设备的正常运转.当滚动轴承出现局部损伤或缺陷时，会造成周期性冲击振动，轻则使设备产生噪声、振动异常，重则发生机毁人亡等严重事故，为此，对滚动轴承的监测和故障诊断一直是人们研究的热点课题[1].小波包分析是滚动轴承故障诊断较为常用的方法[2-4]，它具有很好的时域和频域局部化分析能力，且具有同时分解高、低频信号的多分辨率能力.但是小波包变换以预设的单一小波函数作为分解信号的基函数，不能根据信号的特点进行自适应分析.Sweldens[5]提出的提升模式的小波变换是第二代小波算法，通过预测和更新算子的最优设计匹配特定的信号，获得一组新的、具有某种期望特性的小波函数和尺度函数，具有很好的自适应能力，非常适合非线性故障信号的分析[6].在提升算法的基础上，文献[7-8]提出了提升小波包应用于滚动轴承的故障诊断，解决了传统小波包小波函数和尺度函数自适应性弱等问题，并取得较好的诊断效果.但是，无论采用小波包还是提升小波包变换，均采用下采样方式进行抽样运算，易造成信息成分丢失和频率混叠等问题.基于此，本文采取优化EEMD方法对初始信号进行降噪，然后利用非抽样提升小波包方法提取滚动轴承的故障特征频率，以此规避信息成分丢失和频率混叠现象，从而实现滚动轴承故障的准确诊断.

1 EEMD降噪

1.1 EEMD原理

经验模态分解(empirical mode decomposition，EMD)能有效处理非线性、非平稳的故障信号，与小波变换相比，具有直观的、直接的、后验的和自适应等优点[9].EEMD是EMD方法的继承和拓展，它有效解决了EMD方法中存在的模态混叠，固有模态分量的物理意义不清以及错误显示信号的时频分布等问题[10].EEMD算法运算过程如下[11]：

Step 1 给被分析信号x(t)分别添加N次均值为零、幅值标准差为常数的高斯白噪声ωi(t)， 构建一个总体信号xi(t)， 即

xi(t)=x(t)+ωi(t),

(1)

式中ωi(t)的强度取决于高斯白噪声标准差与初始信号标准差之比Rstd， i=1,2,…,N.

Step 2 对各个信号xi(t)分别进行EMD分解，获得l个本征模态函数IMF分量和1个残余项ri(t):

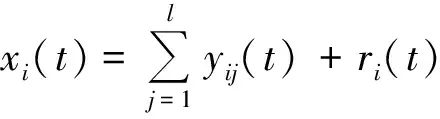
(2)

式中yij(t)是第i次加入高斯白噪声ωi(t)经EMD分解后得到的第j个IMF分量.

Step 3 对所有的IMF分量yij(t)进行均值运算，消除多次加入ωi(t)对真正的IMF影响，最终得到IMF分量yj(t)和残余项r(t):

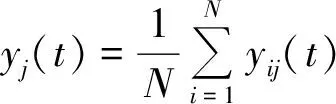
(3)

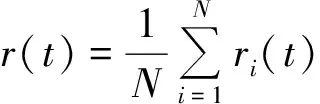
(4)

式中yj(t)为EEMD对信号x(t)分解后得到的第j个IMF分量.

因此，被EEMD分解的信号x(t)可由l个yj(t)和1个r(t)构成，如(5)式所示:

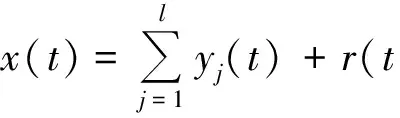
(5)

利用EEMD方法对原始信号分解虽然不会产生模态混叠效应，但由于在分解过程中，不可避免地存在分解误差和插值误差等，从而使EEMD分解得到的各个本征模态函数分量容易出现伪分量；因此，只有剔除分解的IMF伪分量，才能有效提取真正的IMF分量.因伪分量与原始信号的相关程度小，而有效分量与原始信号的相关程度高，所以可以通过相关系数计算准则来筛选有效IMF分量.首先通过经验公式设置辨别伪分量的相关系数阈值μ， 然后根据(6)式(相关系数计算公式)分别计算各IMF分量与原始信号的相关系数值，如果某IMF分量与原始信号的相关系数值小于μ值，则视为伪分量，否则视为有效分量.

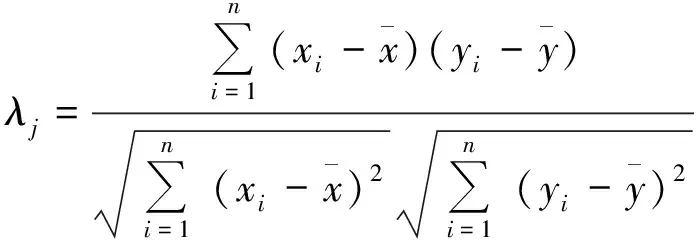
(6)

滚动轴承正常工作时，其振动幅值呈现正态分布，一旦运行出现局部故障，信号就会含有很高的冲击成分，从而使振动幅值偏离正态分布；因此，引入峭度系数能够符合冲击信号的特征，即能够很好地表征故障分量.峭度系数的数学表达式为

(7)

式中Kv为峭度系数， δ为初始信号的标准差.

一般而言，隐含随机噪声的振动信号经EEMD分解得到的高频IMF分量即为噪声信号，如果滚动轴承处于正常运行状况，那么可直接将高频分量剔除即达到降噪效果.但是，若滚动轴承出现局部故障,即信号中隐含冲击成分，此时的冲击成分信息也处于高频段，如果仍然按照直接剔除噪声信号的方法剔除高频IMF分量，则会导致表征故障信息的高频分量直接被剔除.针对这种情况，本文采用相关系数与峭度系数相结合的相关系数-峭度准则来优化EEMD筛选有效的IMF分量，具体的筛选步骤如下：

1) 利用EEMD对原始信号进行分解，得到一组IMF分量；

2) 根据(6)式分别计算各个IMF分量与原始信号的相关系数；

3) 根据实际情况，结合经验公式，设置相关系数阈值μ， 将相关系数小于μ值的IMF分量视为伪分量并直接剔除；

4) 根据(7)式，对剩余的IMF分量分别计算其峭度值，选取峭度值位于前3位的IMF分量作为有效分量进行重构，从而达到降噪目的.

2 非抽样提升小波包算法

Sweldens首次提出提升模式的小波变换理论，其分解过程由剖分、预测和更新3个步骤构成.传统的提升小波或小波包变换均是基于抽样运算的变换方法，容易造成信息成分丢失和频率混叠问题，文献[12]提出的非抽样提升小波包算法有效地解决了该问题.

2.1 非抽样提升小波包分解算法

(8)

(9)

[k-2(s-1)(N+1)+i]},

(10)

(11)

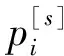
2.2 非抽样提升小波包重构算法

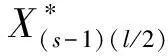
(12)

[k-2(s-1)(N+1)+i]},

(13)

(14)

3 信号仿真

3.1 相关系数-峭度准则的EEMD降噪仿真

假设一正弦信号x1(t)=sin 0.03t，为了体现x1(t)信号中含有冲击成分，向x1(t)信号中添加矩形方波信号x2(t), 然后将x1(t)和x2(t)合成为x(t)=x1(t)+x2(t).x1(t)、x2(t)两种信号的采样点数均为1 000， 如图1所示.

图1 x1(t)、x2(t)和x(t)信号

利用EEMD方法对信号x(t)进行分解，其中在EEMD算法中设置Rstd=0.2， 添加高斯白噪声次数为1 000， 得到8个IMF分量和1个残余分量，如图2所示.

根据(6)式分别计算8个IMF分量与原始信号x(t)的相关系数，计算结果如表1所示.

图2 EEMD分解结果

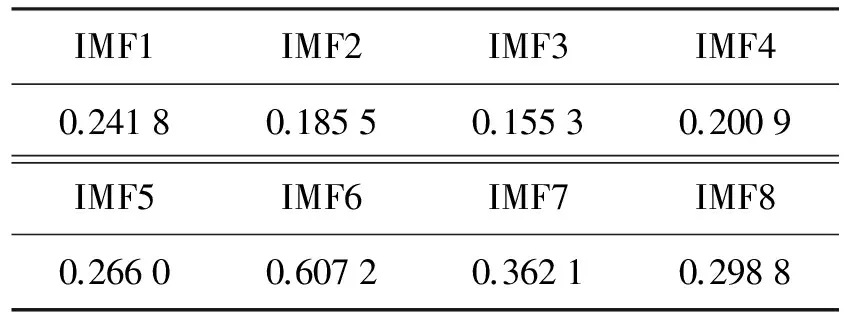
IMF1IMF2IMF3IMF40．24180．18550．15530．2009IMF5IMF6IMF7IMF80．26600．60720．36210．2988

根据经验公式，设置IMF分量相关系数阈值μ=0.2， 由于分量IMF2、IMF3的相关系数都小于0.2， 因此将其剔除.

根据(7)式分别计算剩余的IMF分量的峭度值，计算结果如表2所示.选取表2中峭度值位于前3位的IMF分量，即IMF4、IMF5和IMF6分量，然后将这3个分量进行重构，从而得到降噪信号.图3表明降噪效果比较理想，能基本上保留原始信号的有效成分，过滤掉了噪声信号；因此，基于相关系数-峭度准则的EEMD降噪方法是有效、可行的.

表2 相关程度高的IMF分量的峭度值

图3 x(t)信号的降噪效果

3.2 抗频率混叠信号仿真

为了检验非抽样提升小波包方法的抗频率混叠能力，假设某滚动轴承振动信号的转频为30 Hz， 其故障特征频率为50 Hz.另外，还有2倍频100 Hz和3倍频150 Hz等故障成分，表达式为y(t)=sin(2π×30t)+sin(2π×50 t)+sin(2π×100t)+sin(2π×150 t).采样频率为1 000 Hz， 采样长度为2 048个点.利用非抽样提升小波包和传统小波包分别对分析信号进行三层分解，分解结果的频谱分别如图4和图5所示，考虑篇幅原因，图中仅给出前4个频带的频谱.

从图4可看出，图中除了有效频率30、50、100、150 Hz外，还存在75.2、95.21、174.8、225.1、274.9 Hz等频率(图中用箭头↘标出)，而图5中除了有效频率外没有其他频率成分信号.由此可见，传统小波包因采取抽样运算导致频谱中出现频率混叠现象，而非抽样提升小波包采取非抽样运算方式有效避免了频率混叠.

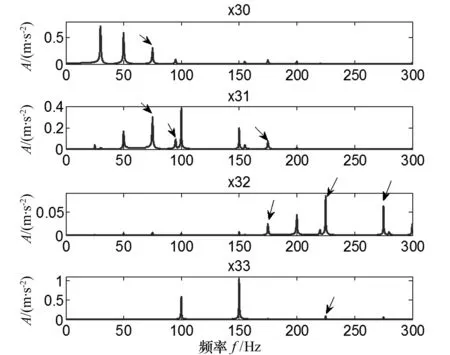
图4 传统小波包频谱

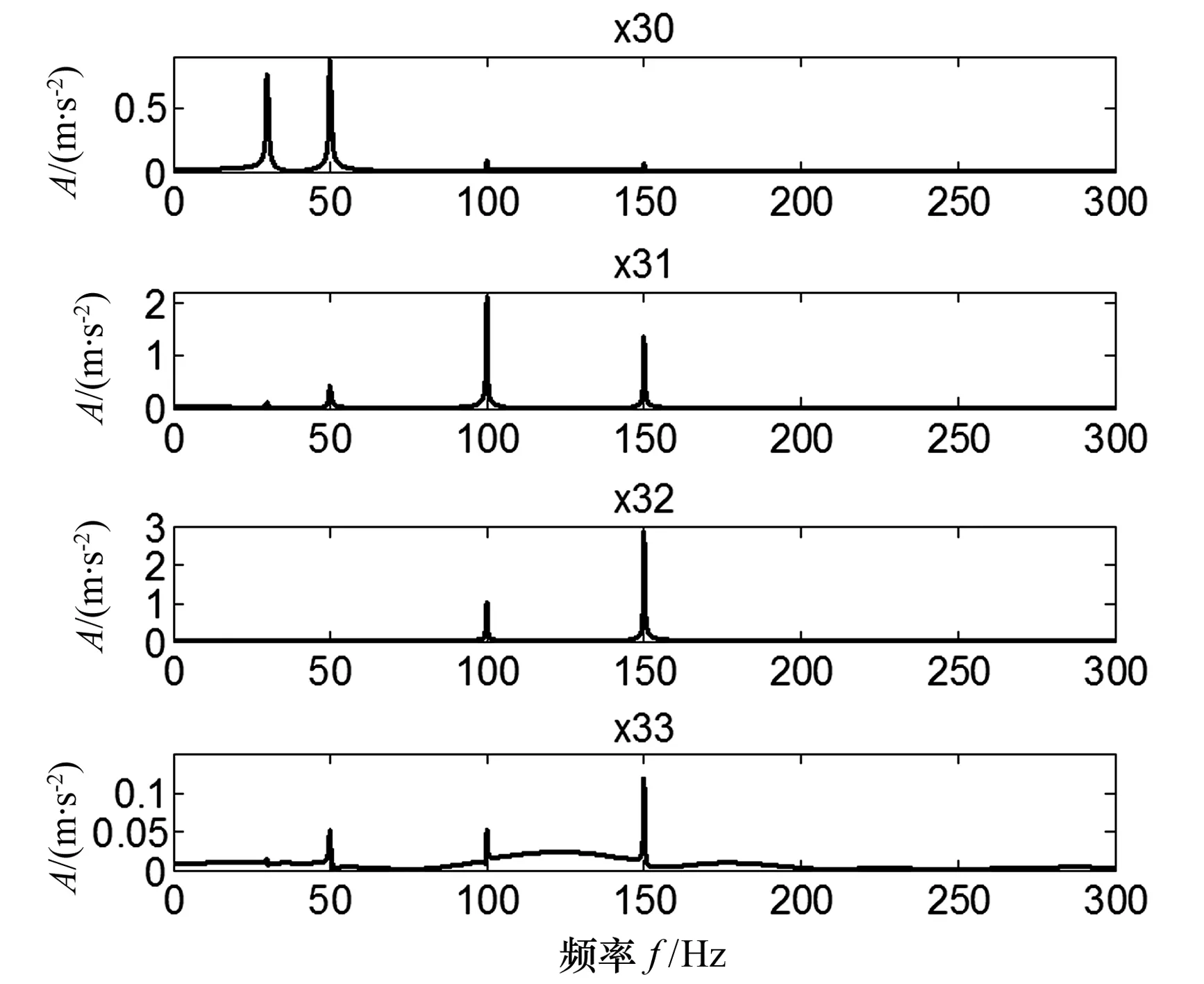
图5 非抽样提升小波包频谱

4 应用实例

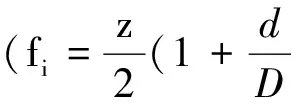
对采集的轴承内圈初始信号进行故障诊断的过程如下：

1) 利用EEMD方法对图6(a)的原始信号进行分解，在EEMD算法中设置Rstd=0.2，添加高斯白噪声次数为1 000，由此得到9个IMF分量和1个残余分量，如图7所示.

2) 分别计算9个IMF分量与轴承内圈原始信号的相关系数，结果如表3所示.

3) 根据经验公式，设置IMF分量相关系数阈值μ=0.1，由于分量IMF5—IMF9的相关系数都小于0.1，因此将其剔除.

4) 分别计算剩余的IMF1—IMF4分量的峭度值，结果如表4所示.选取表4中峭度值位于前3位的IMF分量，即IMF2、IMF3和IMF4分量，并将这3个分量进行重构，从而得到降噪信号，降噪结果如图6(b)所示.

5) 采用非抽样提升小波包方法进行三层分解，利用Hilbert变换进行包络解调分析，最终获得滚动轴承内圈的频谱，如图8(b)所示.

同时，采用传统小波包方法对滚动轴承原始信号进行消噪，随后进行小波包三层分解，最后也利用Hilbert变换进行包络解调分析得到诊断频谱图，如图8(a)所示.

图6 滚动轴承内圈信号消噪前后情况的比较

以上诊断结果表明：①传统小波包诊断滚动轴承内圈的故障特征频率(基频)为130.90 Hz，非抽样提升小波包诊断的基频为126.10 Hz，两种方法诊断出的基频与理论基频的误差分别为3.59%和0.21%，后者的诊断精度更高；②两种方法虽然均能诊断滚动轴承内圈的基频，但非抽样提升小波包提取基频的幅值更大，即故障能量值高，表明本文方法提取的故障信息量远远大于传统小波包提取的故障信息量.③非抽样提升小波包有效地提取了滚动轴承内圈基频、2倍频和3倍频等，而传统小波包对2倍频的表征能力较弱，表明实际存在的谐波成分没能体现.因此，本文提出的诊断方法具有很好的应用价值.

图7 EEMD分解轴承内圈信号的结果

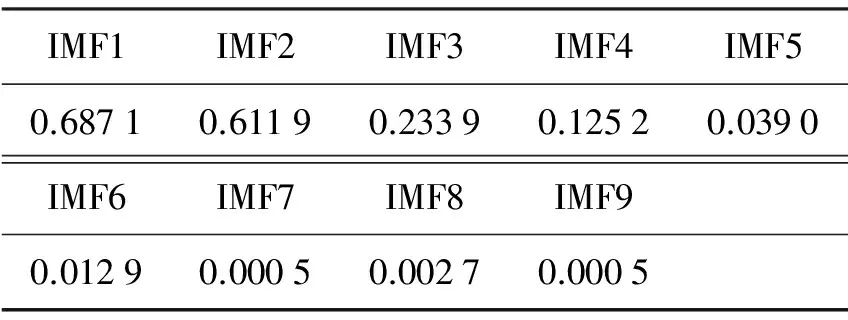
IMF1IMF2IMF3IMF4IMF50．68710．61190．23390．12520．0390IMF6IMF7IMF8IMF90．01290．00050．00270．0005

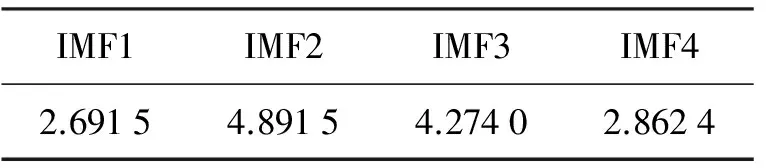
表4 相关程度高的内圈IMF分量的峭度值

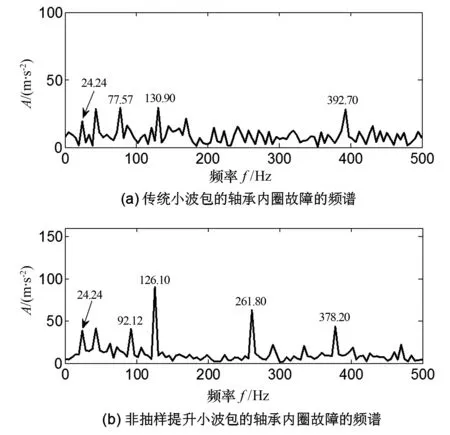
图8 两种方法诊断滚动轴承内圈的频谱

5 结论

本文采用EEMD方法分解原始故障信号，利用相关系数-峭度准则筛选最优的IMF分量进行重构，经仿真实验和实际应用表明，基于相关系数-峭度准则的EEMD方法能很好地实现原始信号的降噪.传统小波包或提升小波包因采用抽样方式运算，易造成频率混叠，而本文采用的非抽样提升小波包方法能够有效避免频率混叠现象，并且通过滚动轴承内圈故障实验证明，非抽样提升小波包比传统小波包具有更好的诊断精度.本文提出的诊断方法可为其他旋转零部件的故障诊断提供参考.

[1] 胡爱军,马万里,唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J].中国电机工程学报,2012,32(11):106-111.

[2] 边杰,王平,梅庆.EEMD结合能量特征和小波降噪的轴承故障诊断[J].广西大学学报:自然科学版,2014,39(6):1206-1211.

[3] 肖顺根，宋萌萌.基于小波包能量神经网络的滚动轴承故障诊断方法[J].机械强度，2014,36(3):340-346.

[4] 韩星，熊静琪，王李立，等.基于小波去噪和最小二乘支持向量机的滚动轴承故障诊断研究[J].机床与液压,2014,42(9):155-158.

[5] Sweldens W. The lifting scheme: a construction of second generation wavelet[J]. SIAM Journal on Mathematics Analysis, 1997,29(2):511-546.

[6] 陈换过,江金寿,李剑敏,等.基于提升小波包和神经网络的结构损伤检测[J].振动、测试与诊断,2013,33(1):116-121.

[7] 谭晓东,覃德泽.提升小波包和改进BP神经网络相融合的新故障诊断算法[J].计算机测量与控制,2014,22(8):2405-2408.

[8] 段晨东,郭研.基于提升小波包变换的滚动轴承包络分析诊断方法[J].农业机械学报,2008,39(5):192-196.

[9] 张超,陈建军.EEMD方法和EMD方法抗模态混叠对比研究[J].振动与冲击，2010，29(S):87-90.

[10] 李昌林,孔凡让,黄伟国,等.基于EEMD和Laplace小波的滚动轴承故障诊断[J].振动与冲击,2014,33(3):63-69.

[11] 陈仁祥,汤宝平,吕中亮.基于相关系数的EEMD转子振动信号降噪方法[J].振动、测试与诊断,2012,32(4):542-546.

[12] 陈敬龙,张来斌,段礼祥，等.基于提升小波包的往复压缩机活塞-缸套磨损故障诊断[J].中国石油大学学报：自然科学版,2011,35(1):130-134.

[13] Jiang Hongkai, He Zhengjia, Duan Chendong. Gearbox fault diagnosis using adaptive redundant lifting scheme[J]. Mechanical Systems and Signal Processing, 2006,20(8):1992-2006.

A new fault diagnosis method of rolling bearing based on EEMD de-noising and undecimated lifting scheme packet

XIAO Shungen， SONG Mengmeng， KONG Qingguang， CHEN Zhaoxiang

(DepartmentofPhysicsandElectricalEngineering,NingdeNormalUniversity,Ningde352100,China)

Traditional wavelet packet in the implied fault diagnosis of rolling bearing exists some problems, such as frequency aliasing, the accuracy is not high, and so on. We propose a fault diagnosis method based on ensemble empirical mode decomposition (EEMD) de-noising and undecimated lifting scheme packet. Using EEMD method to decompose the original signals to obtain a lot of intrinsic mode function (IMF) components, calculated the correlation coefficients between each IMF component and the original signals, and compared with the threshold of correlation coefficients, if the correlation coefficients of IMF were less than the threshold, it would be deemed spurious IMF components and abandoned. The remaining IMF components were used kurtosis criterion to screen the optimal IMF components to reconstruct again, thus achieving the purpose of de-noising. In order to avoid the traditional wavelet packet produced frequency aliasing due to decimated operation, we used undecimated lifting wavelet packet to decompose de-noising signals, and de-noising signals were demodulated with Hilbert transform to get rolling bearing fault location. The simulation experiment and the application examples of rolling bearing inner fault show that: using EEMD to decompose, combining correlation coefficient-kurtosis criterion, attains good de-noising; the undecimated lifting wavelet packet has higher fault diagnosis accuracy than the traditional wavelet packet, and do not exist the problem of frequency aliasing.

rolling bearing; EEMD; correlation coefficient-kurtosis criterion; frequency aliasing; undecimated lifting scheme packet

2015-01-11 作者简介： 肖顺根(1983—)，男，讲师，研究方向为人工智能和机械设备故障诊断.

福建省教育厅A类科技项目(JA14332)；宁德师范学院“服务宁德区域经济和产业发展”专项课题(2013F25，2013F26)；福建省自然科学基金资助项目(2015J01643)

1004-4353(2015)01-0057-07

TH165+.3

A