内积空间中的互不偏基
2015-12-26雷丽霞南华张军
雷丽霞, 南华, 张军*
( 1.延吉市第七中学, 吉林 延吉 133000; 2.延边大学理学院 数学系, 吉林 延吉 133002 )
内积空间中的互不偏基
雷丽霞1, 南华2, 张军2*
( 1.延吉市第七中学, 吉林 延吉 133000; 2.延边大学理学院 数学系, 吉林 延吉 133002 )
将量子信息理论中的互不偏基概念进行了代数化,在内积空间中引进和推广了互不偏基的概念,讨论了欧氏空间中的相关性质,并分别在欧氏空间和酉空间中给出互不偏基的例子.
内积空间; 标准正交基; 互不偏基; 正交矩阵

1 互不偏基的推广

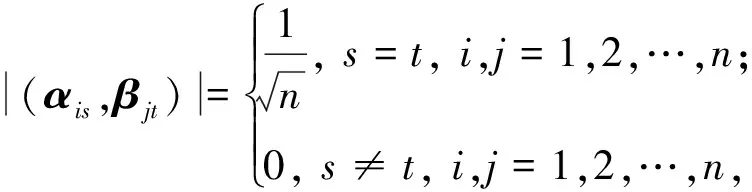
若内积空间有多组标准正交基,且任意两组标准正交基都是(广义)互不偏基,则称其为(广义)互不偏基组.
显然,当定义2中的k取1时,即得定义1的条件和结论.
例1 设F2为2维内积空间,即∀α=(x1,x2), β=(y1,y2)∈F2, 定义内积为
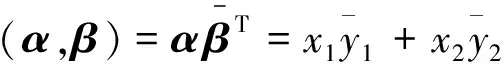
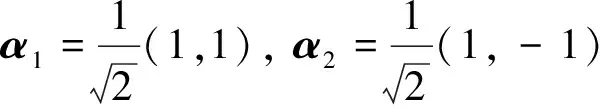
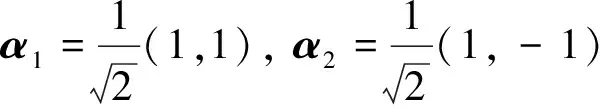
例2 设C3为3维酉空间,即∀α=(x1,x2,x3), β=(y1,y2,y3)∈C3, 定义内积为

取酉空间C3的四组标准正交基[7]:
ε1=(1,0,0), ε2=(0,1,0), ε3=(0,0,1);
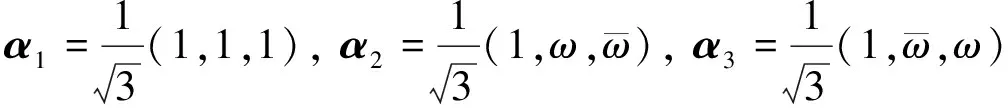
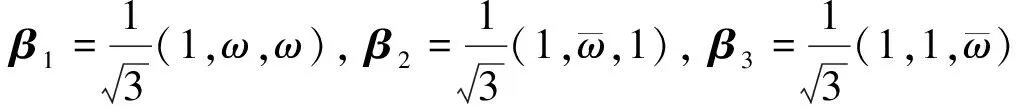
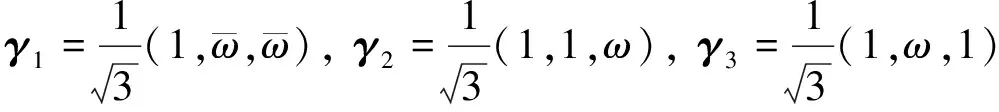
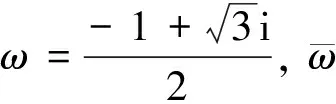



故酉空间C3的四组标准正交基{ε1,ε2,ε3}, {α1,α2,α3}, {β1,β2,β3}, {γ1,γ2,γ3}是互不偏基组.
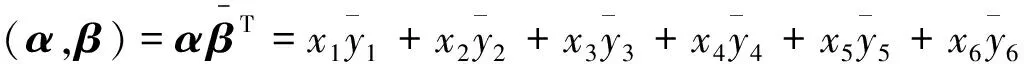
将酉空间C6看成C3×2时,有广义互不偏基组:
ε11=(1,0,0,0,0,0), ε21=(0,1,0,0,0,0), ε12=(0,0,1,0,0,0),
ε22=(0,0,0,1,0,0), ε13=(0,0,0,0,1,0), ε23=(0,0,0,0,0,1);

将酉空间C6看成C2×3时,有广义互不偏基组:
ε11=(1,0,0,0,0,0), ε21=(0,1,0,0,0,0), ε31=(0,0,1,0,0,0),

α12=(0,0,0,1,0,0), α22=(0,0,0,0,1,0), α32=(0,0,0,0,0,1);



广义互不偏基组的构成有多种组合形式,例3中仅给出了其中一种组合.
2 欧氏空间中互不偏基的存在性

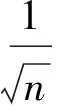
定理1 2m维欧氏空间中存在互不偏基.
证明 (数学归纳法)当m=0时,欧氏空间为1维空间,有1阶正交矩阵A0=(1), 命题显然成立.


故m=k+1时,命题也成立.
由归纳法知, 2m维欧氏空间中存在互不偏基.
例4 欧氏空间R4中的互不偏基.


显然,矩阵A2的4个行向量构成R4的标准正交基,记为α1,α2,α3,α4.

[1] Brierley S, Weigert S. All mutually unbiased bases in dimensions two to five[J]. Quantum Info Comp, 2010,10:803-820.
[2] CHEN Bin, FEI Shaoming. Unextendible maximally entangled bases and mutually unbiased bases [J]. Phys Rev A, 2013,88(3):034301(4).
[3] Adamson R B A, Steinberg A M. Improving quantum state estimation with mutually unbiased bases[J]. Phys Rev Lett, 2010,105(3):030406(4).
[4] Fernández-Pérez A, Klimov A B, Saavedra C. Quantum process reconstruction based on mutually unbiased basis[J]. Phys Rev A, 2011,83(5):052332(6).
[5] YU I C, Lin F L, Huang C Y. Quantum secret sharing with multilevel mutually (un)biased bases[J]. Phys Rev A, 2008,78(1):012344(5).
[6] 同济大学应用数学系.高等代数与解析几何[M].北京:高等教育出版社,2005.
Mutually unbiased bases in inner product space
LEI Lixia1, NAN Hua2, ZHANG Jun2*
( 1.TeachingandGuidingOfficeYanjiNo.7MiddleSchool,Yanji133000,China; 2.DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China)
The concept of mutually unbiased bases in quantum information theory is expressed as algebraic form in this paper, which is defined and extended in inner product space. And the related properties are discussed in Euclidean space. Moreover the examples of mutually unbiased basis are given in Euclidean space and unitary space separately.
inner product space; standard orthogonal bases; mutually unbiased bases; orthogonal matrix
2014-10-20 *通信作者: 张军(1957—),男,教授,研究方向为代数及量子信息理论.
国家自然科学基金资助项目(11361065);吉林省自然科学基金资助项目(201215239)
1004-4353(2015)01-0017-04
O151.2
A
