模糊性与股指期货价格双向偏差研究
2015-12-26冯瑞敏陆家骝
冯瑞敏,陆家骝
中山大学 管理学院,广州 510275
模糊性与股指期货价格双向偏差研究
冯瑞敏,陆家骝
中山大学 管理学院,广州 510275
从模糊性视角研究中国股指期货价格呈现的双向偏差且正向为主的问题。建立模糊环境中投资者连续时间投资消费模型,分析模糊性对投资者最优投资消费决策的影响;在理清模糊性影响资产均衡价格作用机理的基础上,提出模糊性期货定价模型。利用2010年至2014年中国沪深300指数以及指数期货日交易数据,分别运用马尔科夫链蒙特卡洛估计和向量自回归方法对模糊性期货价格模型进行实证检验。研究结果表明,在模糊性条件下,投资者对资产的保留价格受其交易头寸影响,当资产净持有者推动期货交易时,期货价格出现正向偏差,而由资产净卖空者推动时则出现负向偏差;股指期货定价和股票指数服从不同的随机过程,而且两者的持有期收益率存在较大差异;股票指数波动率与股指期货价格偏差的时间序列关系与模糊性期货定价模型的推论一致;中国股指期货市场的模糊性在统计意义和经济意义上均显著。新的期货定价模型阐明了模糊性影响期货价格的作用机制,强调了模糊性对资产价格产生的影响,更好地解释了中国期货价格偏差现象,对未来模糊性衍生品定价有参考意义。
模糊性;股指期货;期货定价;定价偏差;正向偏差
1 引言
股指期货是一种重要的金融衍生工具,它是投资者对冲和管理风险的重要手段,也是投资者构建有效资产组合的重要证券。同时期货作为金融市场信息的主要载体之一,其价格对其他金融资产交易有着价格引导作用。因此,正确理解期货价格是投资者进行正确投资决策、开发其他金融衍生产品并对其合理定价的关键因素。
2010年4月,沪深300股指期货正式上市。股指期货交易提高了中国股票市场流动性和价格发现能力[1],加深了中国资本市场深度[2],对中国金融市场长期健康发展有着积极意义。但是已有研究表明,中国期货市场价格偏差现象(期货交易价格偏离了完美市场中的理论值)频现[3-4]。此外,中国股指期货的偏差方向特征与国外市场有着显著差异。其他资本市场,如新兴市场土耳其[5]、澳大利亚[6]等,大多表现为负向定价偏差。中国股指期货市场价格则呈现双向偏差,且正向偏差现象更为常见[7-8]。虽然现有的期货定价理论能较好地解释国外资本市场期货定价现象,但它们对中国特有的期货定价偏差特征解释力度略显不足。这表明现有的期货定价理论存在局限性,因而研究中国股指期货市场特有的定价偏差现象可以更好地理解金融市场运行规律,为未来衍生品定价提供更可靠的理论依据。此外,分析产生正向定价偏差的原因有助于提高中国金融市场的定价效率、促进中国金融市场发展。为此,本研究从模糊性这个新视角建立期货价格模型,以解释中国期货价格特征。
2 相关研究评述
在完美的金融市场中,期货价格 (期货交割价格的无风险利率下的折现值)应该等于股票价格。但在现实中,期货价格偏差却普遍存在,这促使学者和投资者重新考虑现实交易摩擦对期货价格产生的影响。持有成本模型[9-10]考虑税收、借贷成本差异等交易摩擦,改进了定价模型对现实的解释力度。随后,市场交易机制(如现货市场卖空约束)也被纳入持有成本模型中。持有成本模型确定了期货价格有效理论价格区间,解释了大部分价格偏差。然而它并不能解释股指现货与期货市场之间的动态关系,尤其是价格偏差的系统性特征,如期货价格偏差呈现的负向性、偏差程度的均值回归等[11]。随后发展出来的随机利率期货价格模型[12]能较好地解释国外股指期货市场出现的负向价格偏差、偏差均值回归等现象。然而从模型结论看,持有成本模型和随机利率模型都倾向于解释股指期货价格的负向偏差,对于中国股指期货价格的双向偏差,尤其是频繁的正向偏差现象解释力度较弱。
经典模型、持有成本模型和随机利率模型都建立在将不确定性简化为风险的假设上,此时经济体中的不确定性由单个概率测度(主观或者客观)刻画。但是风险只是不确定性中一种特殊的类型,不能涵盖投资者面临的大部分的不确定性[13]。在风险框架下,只存在唯一的概率测度用来衡量资产未来收益。期货合约在行权日的收益与股票相等,套利机制作用下期货现值等于股票价格。同时,由于期货与股票未来收益相等,当两者出现价格偏离时,投资者只持有价格较低的证券。投资者最优投资决策也使期权价格与股票价格相等。因此,无套利机会机制和投资者决策保证了风险条件下的期货价格等于股票价格,不存在价格偏差。在更广义的不确定性环境即模糊性环境中,投资者找不到一个合适的概率测度能刻画经济体中的不确定性[14],他将用概率测度集合描述不确定性。对应于该概率集合中每一个概率测度期货的未来收益都有一个折现值。因为模糊性环境中投资者拥有的信息量不足以辨别出概率测度集中于哪个概率更符合现实[15-16]。在投资者眼中这些折现值都是可能的期货价格,它们组成了期货可行价格集合。当期货价格等于可行价格集合中的任一值时,无套利机制和投资者投资决策都不能消除期货价格偏差。
一方面,由于套利机会在模糊性环境中覆盖的范围更小,所以无套利机制在模糊性环境中产生的价格约束能力相对较弱。TIAN et al.[17]定义了模糊性环境中套利机会,即如果一个自融资的交易策略保证未来所有状态下收益非负且今天获得确定性收益,或者今天获得一个非负收益且未来对应的每一个概率测度集合都存在一个非零测度的概率可以获得正收益,那么这个自融资交易策略是一个套利机会。根据这个套利机会的定义,当期货价格等于可行价格集合中的任一价格,期货市场都不存在套利机会。因此,模糊性环境下的无套利机制不能确保在交割日前期货价格等于股票价格,期货价格偏差可能出现。事实上,POLKOVNICHENKO[18]已指出,即使资产数量趋向无穷大并且定价因子明确,无套利定价也不能消除模糊性环境中的定价偏差。
另一方面,在模糊性环境均衡价格下,投资者不一定参与期货交易。模糊性厌恶型投资者会对未来做出相对保守的决策,即最优化最坏情景下的投资策略和消费策略[19]。此时只有当期货价格低于期货可行价格集合的最小值时,他才会买入期货;只有当期货价格高于可行价格集合的最大值时,他才会卖出期货;而当资产价格处于可行价格集合范围内时,投资者不参与期货交易[20]。因此模糊环境中市场均衡价格是一个价格区间,而非一个确定值[21-22]。均衡定价区间表明模糊性是期货价格偏差现象的一个合理的解释。
除了股票定价,其他资产的模糊性定价的研究在近年也有长足的发展[23-24]。GAGLIARDINI et al.[25]利用模糊性和模糊厌恶解释利率的期限结构现象;DRECHSLER[26]和LIU et al.[27]从模糊性视角解读价外看跌期权价格相对高、波动率溢价等传统金融异象;FARIA et al.[28]和EPSTEIN et al.[29]分别给出扩散项和波动率存在模糊性时的期权定价模型。此外,BAUM et al.[30]和GUO[31]发现企业的信用违约互换(CDS)中过高的信用溢价是由模糊性造成的。这些研究表明模糊性对多种类型的资产价格都产生重要影响,因此有必要分析模糊性对期货价格产生的影响。
然而目前关于模糊性期货定价的研究还较少,在笔者了解的范围内尚未有直接讨论模糊性对期货价格的影响的研究。这一定程度上是因为传统单一定价核方法(如代表性投资者均衡模型)在分析模糊性期货价格问题上存在一定的局限,单一定价核忽视了投资者在模糊性环境中可能产生的内生性意见分歧。针对这个局限,本研究引入多参与者均衡模型。事实上多参与者均衡模型是研究到期日收益与标的资产相同的衍生资产模糊性定价的一个有效方法。在模糊性商品远期合约交易的分析中大多引入生产者和对冲者两个交易者[32-35],这些模糊性远期合约交易模型明确了多交易对手对于均衡价格的重要性,这对于模糊性期货交易分析具有启发意义。但股指期货合约和商品远期合约的标的资产存在两个显著差异。首先,标的资产的供给存在差异。商品供给可由生产者自由决定,而股票的供给相对固定。其次,标的资产交易时间存在差异。商品远期合约中的标的资产只参与未来时期的交易,而期货合约的标的资产则能同时参与当期和未来时期的交易。这使期货价格不仅受到交易者跨期边际效用的限制,还受到当期股票价格的影响。标的资产的差异性使模糊性期货价格模型具有自身特性。为此本研究尝试建立模糊性期货定价模型,以更好地分析模糊性对不同类型资产的定价产生的影响。
结合模糊性期货定价模型,本研究提出测定中国金融市场模糊性的可行方法。BOYARCHENKO[36]利用危机前后CDS溢价的变动测定投资模糊性系数的改变,但是相应衍生产品的缺失使该方法不适用于中国金融市场。JEONG et al.[37]收集股票市场、消费市场和劳动市场数据,根据基于消费的宏观金融模型估计投资者的模糊性厌恶系数。由于依赖宏观数据,该方法估计的市场模糊性存在样本时间跨度较长、更新频率较低的缺陷。相较而言,利用期货价格测定市场模糊性更为便捷。一方面期货价格数据更为易得,收集成本较低;另一方面,期货价格数据更新速度较快,可以在较短的时间范围内跟踪市场模糊性的变动。因此,模糊性期货定价模型提供了快速有效测量市场模糊性的依据。
在此基础上,本研究对中国股指期货市场的模糊性溢价进行定量分析,为以后模糊性溢价的定量分析提供一种解决思路。
3 模糊性期货定价模型
3.1 模型基本假设
基于模糊性厌恶的思想,GILBOA et al.[38]提出最大最小化期望效用函数刻画模糊厌恶型投资者偏好。投资者会在概率测度集合中选取最小化其期望效用的概率测度作为衡量其期望效用的标准,并以此为依据制定最大化其效用的投资消费策略。EPSTEIN et al.[22]将两期的模糊厌恶效用函数拓展至多期情景。国内外学者沿着这一思路定义投资者模糊厌恶型偏好[19,39-40]。本研究假设投资者具有模糊厌恶偏好,其效用函数为
(1)

3.1.1 仅存在风险的情况(特殊情况)
当经济体中未来的不确定性简化为风险时,股票价格过程可以由单个概率测度p刻画。在该概率测度下,时间t的股票价格为St,股票市场波动率为vt,这两个状态变量的随机过程满足

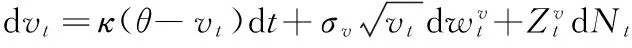
(2)
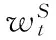
状态变量服从的随机过程包括布朗运动和跳跃两个部分,相对于CHEN et al.[39]仅包含布朗运动的随机过程假设更贴合股票市场实际表现。事实上,状态变量随机过程(2)式是刻画观察得到的股票价格的较为一般的形式,而且该假设具有较高的灵活程度,在一定的条件下可转化为SV和SVJ等模型[41-43]。
3.1.2 存在模糊性的情况(一般情况)
现实交易过程中由于经验数据限制、对未来的信息量有限等原因,投资者不能确信一个唯一概率测度。根据现阶段信息,投资者能得到一个与客观状态最为接近的概率测度作为参考点(即基准概率测度p)以及基准概率测度附近的一些概率测度作为可能的测度。这些概率测度组成的概率测度集合为ϑ,模糊性厌恶偏好使投资者在做经济决策时会考虑ϑ对经济后果产生的影响。为了论述方便,由参数向量α标记概率测度集合中概率测度q(α)。根据Gisarnov定理,概率测度和基准概率测度的布朗运动部分满足
(3)
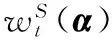
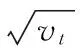
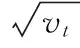
(4)
α刻画了新概率测度对原概率测度的偏离程度,因此可以用偏离程度参数向量α代表新的概率测度,α=(αS,αv,αλ,αμy,ασ,αμv)。相应地,偏离程度参数向量集合{α}等价于可能的概率测度集合ϑ。直观地,可以利用参数区间划定偏离程度向量集合。参数向量α满足
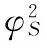
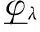
φ≫0
(5)
参数范围向量φ划定了偏离程度参数向量集合{α},因此在给定基准概率测度的情况下,φ确定了概率测度集合ϑ,也即投资者面临的模糊性可以由参数范围向量φ刻画。这个利用参数范围刻画概率测度集合的方法与GARLAPPI et al.[44]参数置信区间刻画模糊性的方法一致。
3.2 股票-债券均衡模型

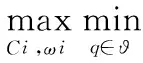
(6)
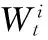
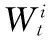
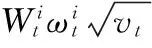
(7)
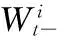
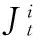
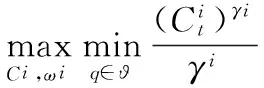
(8)
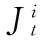

(9)

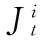
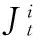
(10)

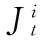
(11)
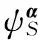
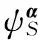
(12)
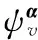
(13)
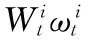

定理1 模糊性参数取值
(1)布朗运动部分的模糊性参数αS和αv的取值取决于投资者持有资产的头寸以及他们对待波动率的偏好,即αS=1ωitφS,φS>0;αv=1Jvφv,φv>0,即

其中,1ωit为投资头寸的示性函数,1Jv为价值函数关于波动率的偏导函数Jv的示性函数。
(2)跳跃部分模糊性参数取值
股票价格跳跃幅度:
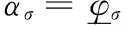
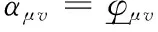
投资者最终选取的概率测度随投资者投资决策的变动而变动。将投资者的模糊性参数代入(9)式,并根据一阶条件求解投资者最优的消费决策和投资决策。
定理2 消费决策和投资决策
时间t投资者的最优消费为
(14)
最优投资于股票的比率为
(15)
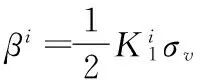

投资者持有的信息是相同的,不存在私有信息,即假设投资者面临的模糊性和模糊性偏好一致。当投资者对待风险偏好和波动偏好一致时,投资者持有相同方向的资产头寸。然而在现实资本市场中,既存在持有股票的投资者也存在卖空股票的投资者,因此投资者偏好存在一定的差异。本研究假设经济体中的投资者均为风险厌恶(γi<1),这与投资者厌恶不确定性的偏好保持一致。为方便论述,假设投资者的风险偏好一致(即所有投资者风险厌恶系数等于市场风险厌恶系数γ,γi=γ),投资者对待波动率偏好的差异驱使他们持有不同的资产头寸。假设投资者忍受波动率的程度在市场中均匀分布,即βi∈[-1,1]。在均衡时,整个资本市场的总需求为1,即
(16)
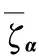
(17)
虽然存在模糊性,但是一方面均衡时客观概率测度下的股票价格满足的随机过程与基准概率测度下的随机过程一致;另一方面由于投资者的交易不影响股票价格波动率,股票价格波动率依然满足基准概率测度。均衡时状态变量满足的客观概率下的随机过程与投资者观测的基准概率测度下的随机过程一致,基准概率测度即为市场观测的客观概率测度。根据均衡时的股票价格可以建立起金融资产在股票市场中的影子价格,该影子价格可以通过风险中性概率Q测度表达。
当经济体只存在股票和债券两个市场且实现均衡时,具有模糊性异质性的所有投资者的整体行为可用市场代表性投资者表示,也即代表性投资者等价于市场。
定理3 风险中性股票价格随机过程
具有模糊性的股票-债券市场实现均衡时,股票价格满足的随机过程使风险厌恶型代表性投资者在基准概率测度p下的最优消费决策等于股利、最优投资比率等于1。代表性投资者的消费投资决策问题为
(18)
其中,Ep为基于基准概率测度p的期望。此时存在与代表性投资者偏好相对应的风险中性测度Q,在该测度下股票价格表现为
(19)

这与传统的资产定价得到的结论相同。该风险中性概率测度提供了客观概率测度下随机过程与资产价格的关系,在这个价值衡量标准下,股票市场认为的未来时间T、股票价格ST与现货价格之间应满足St,则

(20)
其中,rτ为未来时间区间[t,T]中时刻τ的无风险利率。作为基准,在时间t市场对未来时刻T股票价格的均衡预期为Ft,它等于未来股票价格在风险中性测度Q下的期望,即

(21)
其中,EQ为基于风险中性测度Q的期望。在风险中性概率测度Q下,Ft满足的随机过程为
(22)
记股票市场对未来股票价格的现值(也即期货价格)为ft,ft=Ftexp[-rt(T-t)]。由(22)式可知,在风险中性概率测度下其满足的随机过程为
(23)
根据Gisarnov定理,在基准概率测度p下,期货价格服从相同的随机过程,也即
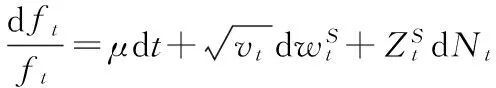
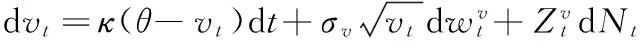
(24)
该随机过程与股票价格满足的随机过程相同。因为在到期日期货价格与股票价格必然相等,因此当金融市场仅存在股票和债券两个资产时,期货价格等于股票价格。该期货价格和经典金融理论下的价格一致。因此股票价格是期货价格在基准概率测度下的影子价格。然而在期货市场现实的交易价格不一定等于未来股票价格在股票现货市场中影子价格。
3.3 股票-债券-期货市场模型
股票是期货的标的资产,因而(24)式实际上是期货价格在基准概率测度下服从的随机过程。当存在模糊性时,期货价格并不一定与股票价格相等。首先,无套利机制不能保证模糊环境中的期货价格与股票价格相等。参与股票市场和期货市场的投资者人数、买卖头寸等存在差异,两个市场存在不同的价格变动的可能。当期货价格属于可行价格集合时,多个概率测度使投资者难以构造一个具有确定性收益的资产。因此,模糊性使投资者把基准模型附近的概率测度纳入考虑范围内。此时期货满足的随机过程为

(25)
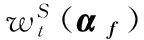

φf的大小取决于期货市场中的信息效率。
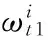

(26)
股票市场和期货市场交易的资产不同,模糊性程度也会不同。当投资者可以同时投资股票市场和期货市场,均衡时期货市场的模糊性程度与股票市场相等,也即φf=φ,否则模糊性程度较高的市场将被模糊性程度较低的市场取代。
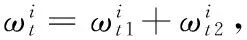
抛补型的投资者可以自身构造出与期货收益率一致的资产组合,只有当期货价格具有竞争力时,他们才会选择期货市场。在股票市场风险中性概率测度下,期货价格满足的随机过程为
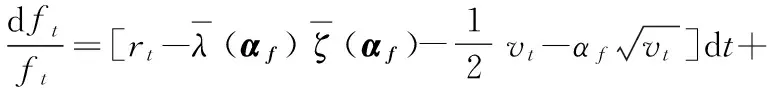

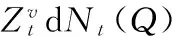
(27)
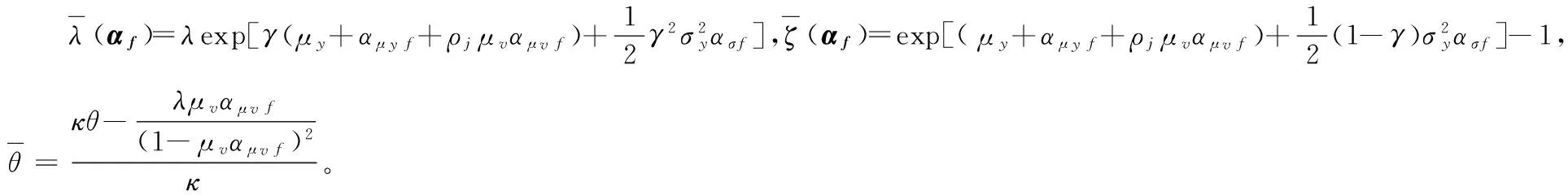
比较(27)式与风险中性概率测度下的期货价格随机过程(23)式可以发现,期货价格随机过程和影子价格随机过程存在一定的差异,两者的差异由投资者最终选择衡量的概率测度q(αf)与基准概率测度之间的差异决定。由于可选的概率测度q(αf)与基准概率测度的差异在范围φf内,因此期货价格在一定的范围区间内,即
(28)
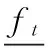


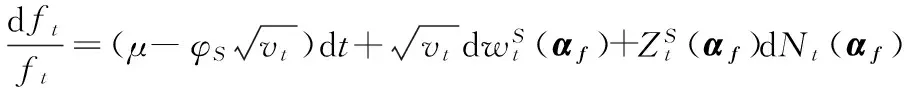

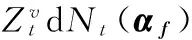
(29)
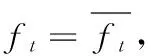
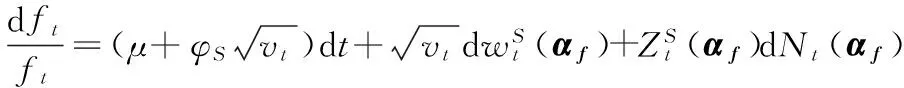
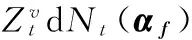
(30)
因此,在存在模糊性的经济环境中,期货价格偏差存在双向偏差的可能。期货市场价格的最终实现及其满足的随机过程由期货市场主要推动者决定。因为φS>0,所以当卖空者推动期货交易时,期货价格的漂移率低于影子价格的漂移率,期货价格将低于影子价格,因而期货市场价格呈现负偏差;当资产净持有者推动期货期货交易时,期货价格漂移率高于溢价价格的漂移率,期货价格将高于影子价格,因而期货市场价格呈现正偏差。中国资本市场投资者存在较强的融资约束,而持有期货需要的初始资本较少,资产净持有者更倾向持有期货,从而形成以资产净持有者推动为主的期货市场,期货价格出现正向偏差。在股市低迷时,中国资本市场存在的卖空约束会使资产净卖空者更愿意进入期货市场,此时期货市场由卖空者推动,期货价格为负向偏差。
4 股票指数和股指期货对比分析
以上论述表明,期货价格和股票价格在模糊性环境中呈现与风险环境中不同的关系,即在风险环境中期货价格唯一,期货价格与股票价格相等;在模糊性环境中期货价格在一定的区间内变动,不一定与股票价格相等。期货市场推动者持有头寸的差异使期货市场呈现双向偏差,下面利用中国股指期货实际交易数据对本研究提出的模糊性期货定价模型进行实证检验。首先,对比股票指数和股指期货的收益率以及服从的随机过程,判断是否满足传统风险环境的等价关系;然后,根据模糊性期货定价的推论,检验波动率和期货价格偏差在时间序列中的关系;最后,对中国金融市场的模糊性进行定量衡量,用模糊性解释中国期货市场和股票市场的偏离程度。
本研究采用2010年4月16日至2014年12月19日到期的所有期货合约(共56个)日交易数据,同时也截取相同时间区间内沪深300指数的日交易数据,数据均来自万德数据库。
4.1 股票指数和股指期货收益率比较
在本研究分析的时间区间内,股票指数和股指期货价格基差(即股票指数与股指期货之差)的走势见图1。股票指数和期货指数存在一定的差异,但总体走势一致,基差基本在[-100, 50]范围内变动。中国股票市场从2010年4月的3 400点经过较为完整的周期后在2014年底重新回到3 400多点。在样本区间内中国股票市场经历了完整的涨跌周期,能较全面地反映模糊性在不同阶段定价产生的影响。
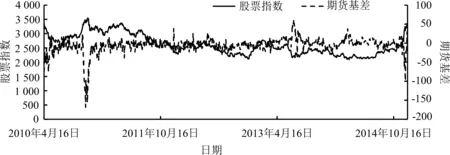
图1 股票指数与股指期货价格基差走势Figure 1 Trends of Stock Index and Stock Index Future Price Basis
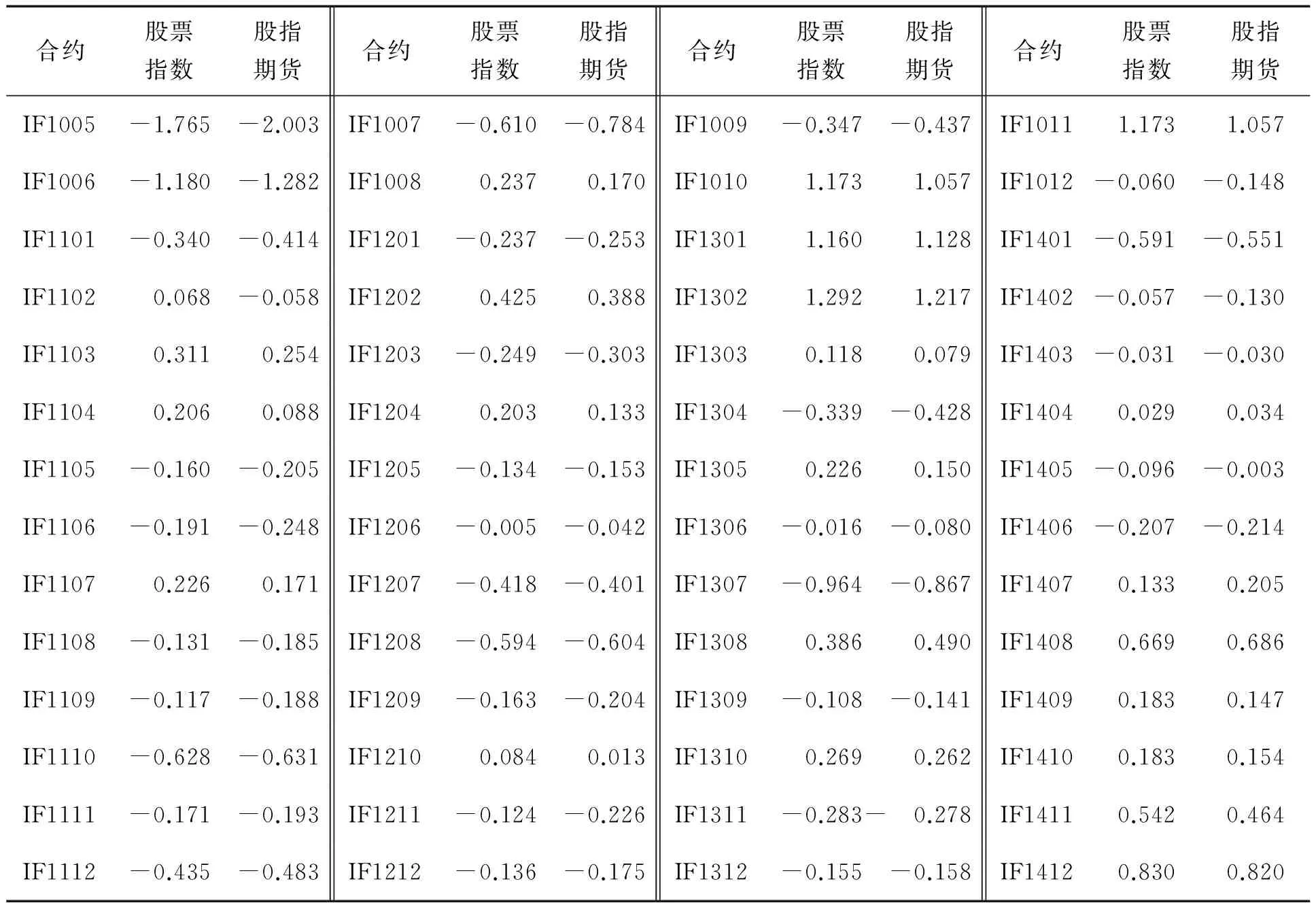
合约股票指数股指期货合约股票指数股指期货合约股票指数股指期货合约股票指数股指期货IF1005-1.765-2.003IF1007-0.610-0.784IF1009-0.347-0.437IF10111.1731.057IF1006-1.180-1.282IF10080.2370.170IF10101.1731.057IF1012-0.060-0.148IF1101-0.340-0.414IF1201-0.237-0.253IF13011.1601.128IF1401-0.591-0.551IF11020.068-0.058IF12020.4250.388IF13021.2921.217IF1402-0.057-0.130IF11030.3110.254IF1203-0.249-0.303IF13030.1180.079IF1403-0.031-0.030IF11040.2060.088IF12040.2030.133IF1304-0.339-0.428IF14040.0290.034IF1105-0.160-0.205IF1205-0.134-0.153IF13050.2260.150IF1405-0.096-0.003IF1106-0.191-0.248IF1206-0.005-0.042IF1306-0.016-0.080IF1406-0.207-0.214IF11070.2260.171IF1207-0.418-0.401IF1307-0.964-0.867IF14070.1330.205IF1108-0.131-0.185IF1208-0.594-0.604IF13080.3860.490IF14080.6690.686IF1109-0.117-0.188IF1209-0.163-0.204IF1309-0.108-0.141IF14090.1830.147IF1110-0.628-0.631IF12100.0840.013IF13100.2690.262IF14100.1830.154IF1111-0.171-0.193IF1211-0.124-0.226IF1311-0.283-0.278IF14110.5420.464IF1112-0.435-0.483IF1212-0.136-0.175IF1312-0.155-0.158IF14120.8300.820
根据传统的完全市场无套利期货定价,股票指数和股指期货应当满足ft=Ste(r-d)·(T-t),因此股指期货持有期收益率rF与股票指数持有期收益率rS之间满足的关系为
rF=rS[1-(r-d)·(T-t)]-(r-d)·(T-t)
(31)
其中,r为无风险利率,d为股票指数的分红率。
目前尚无统一的衡量无风险利率的标准,存款基准利率是衡量中国无风险利率的常用指标之一。由于期货到期时间长短不同,难以确定其一一对应的存款利率,一般的做法是选取活期存款利率为无风险利率,中国活期存款利率为0.350%。为避免存款利率选取差异产生的影响,在计算收益率时直接比较股指期货指数收益率和同时期的股票指数收益率(剔除股息后的收益率),股指期货持有期收益率和相同时期的股票指数年化收益率见表1。除IF1207、 IF1307、 IF1308、 IF1311、IF1401、IF1403、 IF1404、IF1405、 IF1407、 IF1408这10个合约,其余46个合约相应的持有期内股票指数的收益率高于股指期货收益率。股票指数平均持有期收益率为-1.640%,若考虑股息收益率更高。而股指期货持有期收益率为-5.952%,即使加上0.350%的活期存款利率,股指期货的收益率依然低于股票指数收益率。从持有期收益率看,股指期货存在双向偏差,而正向偏差更为普遍。

表2 股票指数和股指期货日收益率描述性统计Table 2 The Descriptive Statistics of Stock Index′s and Stock Index Futures′ Daily Return
为了更直接地观察股票指数和股指期货变动情况,本研究将对比股票指数和股指期货短期收益率分布的差异。一般认为期货市场的信息仅领先股票市场几分钟到十几分钟,为避免信息在不同市场中传播速度差异导致的股票指数与股指期货变动不一致问题,本研究选取日交易数据进行分析。此外,期货合约在发行初期成交量较少,随着合约到期日期临近成交量逐渐放大,为避免流动性溢价对分析产生的影响,本研究选取每个交易日中所有期货合约中最接近到期日的期货合约的交易指数作为当天股指期货指数。从2010年4月16日至2014年12月19日,共有1 135个交易日。
不考虑股息的日收益率为rx(t),rx(t)=100·{log[x(t)]-log[x(t-1)]},x为股票指数或股指期货。股票指数和股指期货每天收益率的描述性统计见表2,股票指数平均日收益率为0.100%,而股指期货的平均日收益率为-0.200%。平均而言,股指期货日收益率低于股票指数日收益率,虽然两者方差接近,但是两者的偏度存在差异,股票指数偏度为-0.135,而股指期货的偏度则为正,为0.064。此外,股指期货收益率分布的厚尾现象更为明显,股票指数的峰度为5.033,而股指期货的峰度为6.684。偏度和峰度的差异表明股票指数与股指期货日收益率的分布形态有较大差别,而且偏差变动(股指期货收益率-股票指数收益率)也呈现厚尾的现象,其峰度为7.533。股票指数与股指期货日收益率的差异存在较大的极端值。因此,从静态比较看,两者的收益率分布存在较大差异。
4.2 股票指数与股指期货随机过程比较分析
进一步分析股票指数和股指期货两个指数服从的随机过程是否一致,经典的拟合股票市场价格水平用随机波动率(SV)、随机波动率带跳(SVJ)和随机波动率关联跳跃(SVCJ)这3个模型。SV模型是在(2)式的基础上,假设不存在跳跃,也即λ=0;SVJ模型是在(2)式的基础上认为只有股票价格存在跳跃,波动率不存在跳跃,也即跳跃幅度率参数μv=0;SVCJ模型是指股票价格满足(2)式的随机过程。本研究分别利用这3个随机模型分析中国股票指数和期货指数随机波动情况。
利用马尔科夫链-蒙特卡洛贝叶斯估计方法(MCMC)对股票指数和期货指数的随机过程的参数和波动率进行估计,这是较为成熟的估算价格随机波动参数的方法,能较好地克服利用最大似然估计或广义矩估计方法估计潜变量面临的“高维度诅咒”,详细的方法参见ERAKER et al.[42]、LI et al.[46]和乔高秀等[47]的研究。样本区间为2010年4月16日至2014年12月19日的股票指数和按照前文方法选取的股指期货。为保证随机抽样能够收敛,参照LI et al.[46]的处理,抽样次数为5万次,前3万次为burn-in抽样,后2万次结果作为参数估计的有效抽样,估计结果见表3。由表3可知,股票指数和股指期货在3个模型中的漂移率μ都为负,股票指数的漂移率μ均不显著,而股指期货的漂移率在SVJ和SVCJ这两个模型中都显著为负,对应于每个模型,股指期货的漂移率都低于相同模型下的股票指数漂移率,表明股指期货的期望收益率低于股票指数的期望收益率,这与前面关于两个指数收益率的静态分析一致。关于波动率方面,股票指数的θ高于股指期货,这与表2中的统计值一致。股指期货的波动率调整速度κ要高于股票指数,意味着股指期货波动率能更快地回复到稳定水平,股指期货市场的灵活程度更高。此外,股指期货面临冲击的程度更高。在SVJ和SVCJ两个模型中,股指期货的跳跃强度λ均大幅度高于股票指数。在SVJ模型中两个指数的收益率跳跃幅度的期望参数μy相差较大,股票指数的为0.068,而股指期货的为0.530。在SVCJ模型中,股票指数和股指期货的ρj均呈现负相关,而这个相关关系在股票市场中表现得更为密切,股票指数的ρj为显著的-0.632,而股指期货的ρj则为-0.203,不显著。
从3个模型的估计结果看,股票指数服从的随机过程与股指期货服从的随机过程存在较大差异。因此,现实交易的股票指数和股指期货价格随机过程并不如(19)式和(23)式一样等价,也即特殊环境(风险环境)下的随机过程并不能很好地刻画现实交易中的股票指数和股指期货价格随机过程。
5 偏差分析
前文已经分析了期货价格与股票价格随机过程之间存在不一致的现象,下面将分析股指期货价格偏差程度以及影响因素。本研究中的偏差主要指期货交易价格相对于其经典理论价格的偏离,在不考虑交易成本(税收、交易费用等)的情况下,期货价格偏差等于期货价格相对于股票价格的偏离,本研究用期货价格和股票价格的对数之差衡量期货价格偏离的程度。图2为偏差的水平走势图,在样本期内,偏差出现较大的波动,且正向和负向偏离均可能出现。图3为偏差的变动图,由图3可知,偏差的变动(偏差收益率)在样本期内呈现较大的波动。
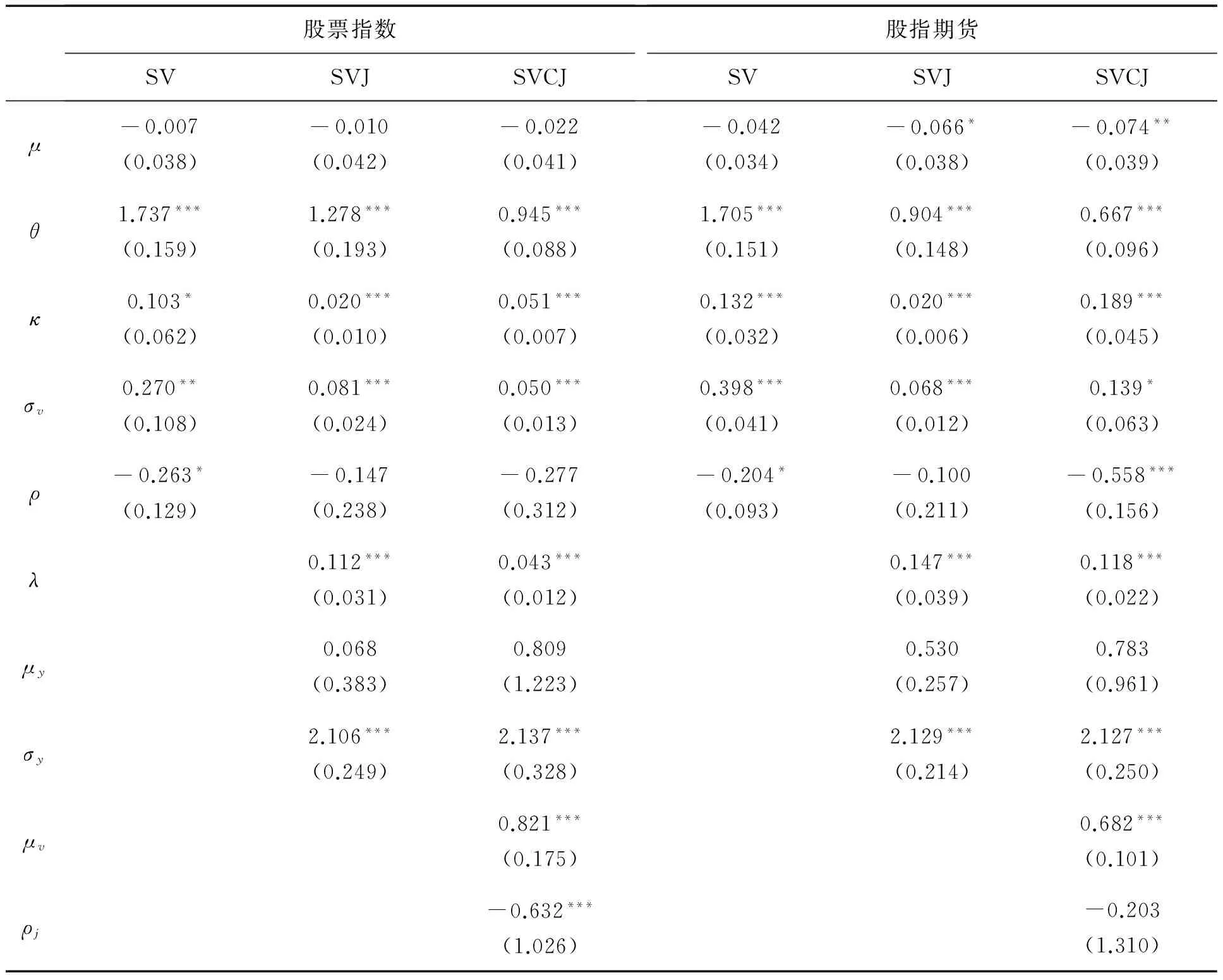
表3 股票指数和股指期货随机过程参数估计Table 3 Stochastic Process′ Parameters Estimation of Stock Index and Stock Index Futures
注:系数估计以天为单位;括号中的数据为系数估计的标准差;*为p<0.100,**为p<0.050,***为p<0.010,下同。
不同的期货价格模型得到的期货价格偏差与偏差变动特征不同,在完美市场无套利机制下不存在偏差,偏差变动为0,即

(32)
随机波动利率模型的偏差变动与波动率值相关,参考HEMLER et al.[12]的研究可得

(33)
由前文可知,模糊性期货定价模型的偏差变动为
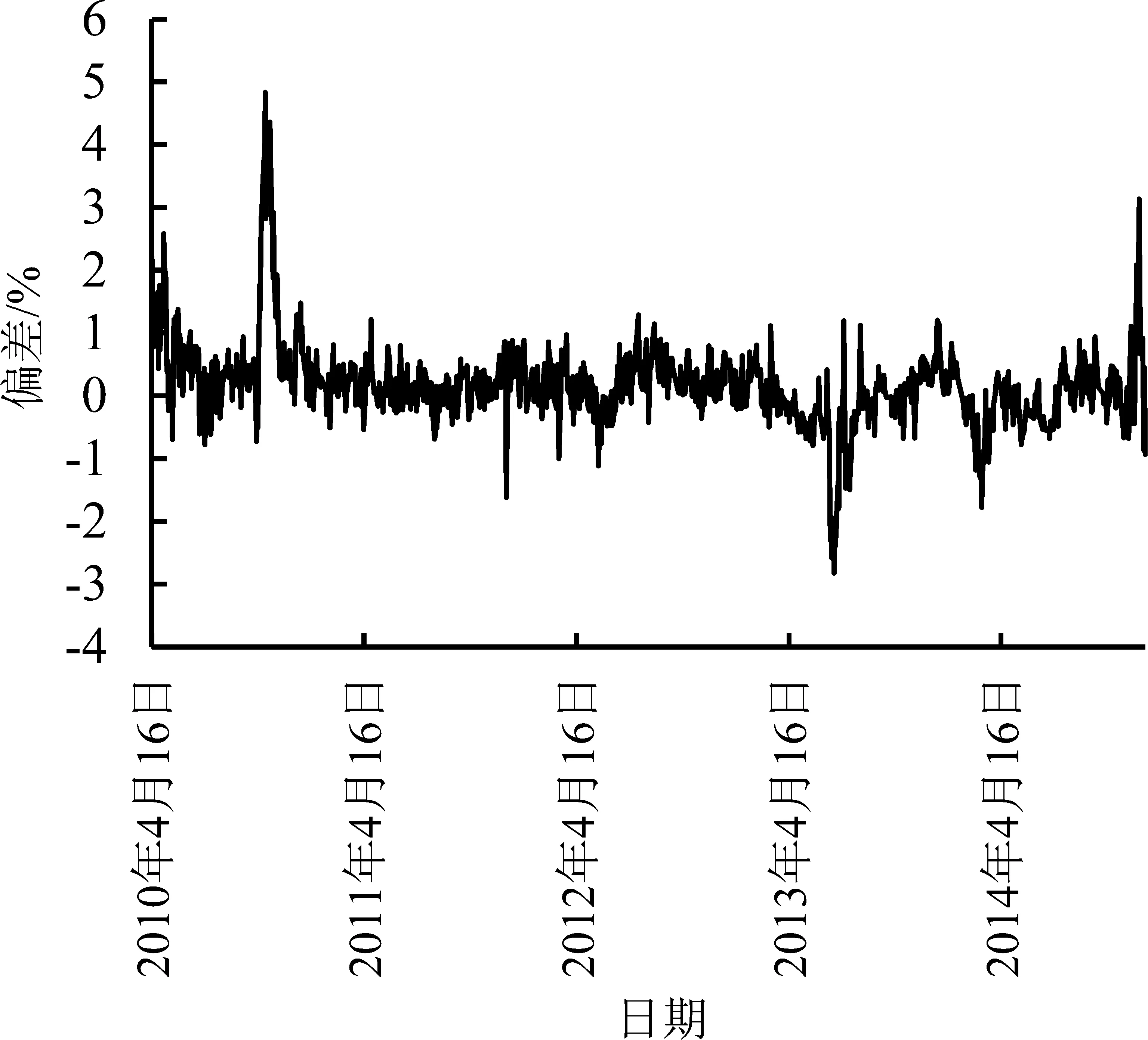
图2 股指期货价格偏差Figure 2 Stock Index Future Price Deviation

(34)
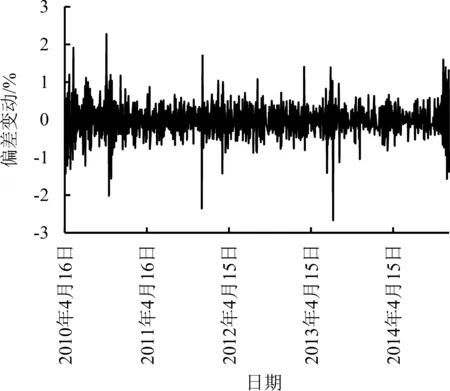
图3 价格偏差变动百分比Figure 3 Percentage Changes of Price Deviation
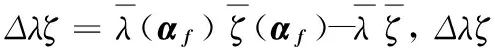
完美市场中期货偏差变动与现实不符,因此本研究只对随机波动率模型和模糊期货定价模型关于偏差变动的关系进行检验。由(2)式可知,状态变量波动率vt与股票价格St相互影响,由(23)式和(24)式可知,状态变量波动率vt与期货价格ft也存在相互影响。为解决两个变量同期之间产生的内生性问题,采用向量自回归(简称VAR)的方法进行分析,回归模型为
yt=c+A1yt-1+A2yt-2+…
(35)
其中,yt为变量向量;c为常数向量;Al为滞后l期系数向量,l=1,2,…。
在样本期内,中国股票指数变动较大,为了避免不同样本时间段选择的偏差对结论产生的影响,本研究对股票指数进行结构突变检验,并根据结构突变点对不同长度的样本区间进行分析。根据BAI et al.[48]的全局最小残差平方和的方法寻找数据结构存在突变的点,在突变结构次数最大值为5的前提下,依据BIC和RSS寻找最优结构突变个数和结构突变点。在样本期内,中国股票指数存在两个结构突变点,分别是2011年9月1日和2012年6月21日。利用MCMC方法估计不同样本期内参数和潜变量,并计算向量自回归分析所需的变量时间序列。
VAR分析前首先对相关时间序列进行平稳性检验,SV、SVJ和SVCJ这3个模型得到的波动率、波动率开方、跳跃变动绝对值以及偏差、偏差绝对值的时间序列都通过了单位根检验,均为平稳时间序列。在不同的样本期内,分别根据AIC和BIC等信息准则选取不同模型(SV,SVJ,SVCJ)向量自回归的最优滞后阶数,然后根据最优滞后阶数进行向量自回归分析,最后对偏差变动和偏差变动绝对值进行格兰杰因果检验。本研究分析的重点是偏差变动,为节省篇幅,这里主要报告偏差的回归结果。

在3个样本期间内,HEMLER et al.[12]期货价格模型的波动率的滞后项对偏差变动的解释力度较弱,其系数基本不显著。而波动率对偏差变动的格兰杰因果检验的p值为0.193,表明即使在10%显著性水平下也不能认为波动率是偏差变动的格兰杰原因。因此,中国期货价格并不支持Hemler & Longstaff期货价格模型。
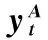
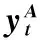
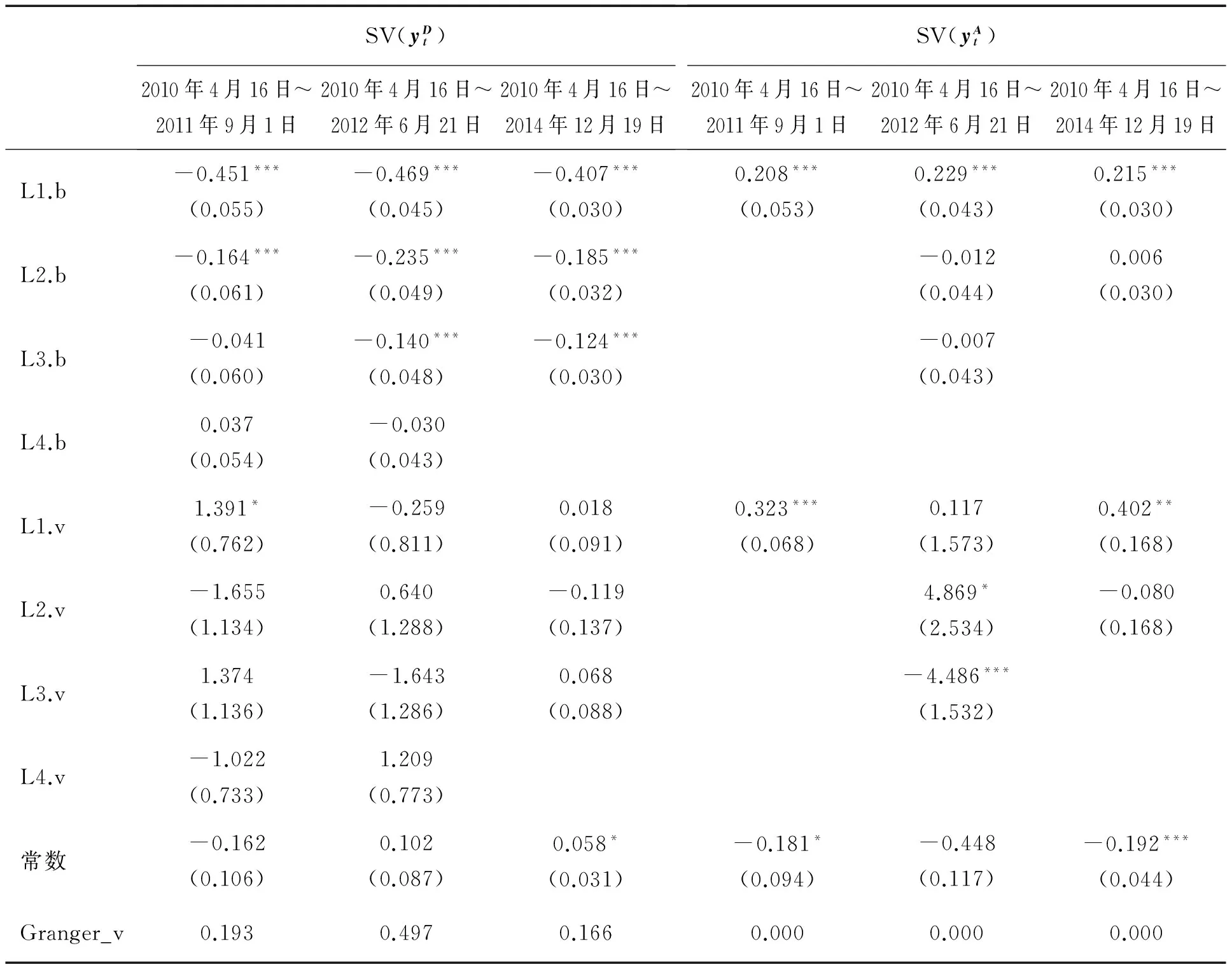
表4 基于SV模型的向量自回归分析Table 4 Vector Auto-Regression Analysis of SV Model
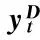
由表5可知,在基于SVJ模型的3个时间段的回归分析中,存在波动率开方的滞后项在5%的显著性水平下显著,其中第1个样本期内波动率开方的滞后1期、第2个样本间内波动率开方的滞后4期以及第3个样本期内波动率开方的滞后3期,而跳跃项的滞后4期、滞后4期和滞后2期分别在3个样本期间内在5%的显著性水平下显著。格兰杰因果检验显示,在样本期2010年4月16日至2011年9月1日和2010年4月16日至2014年12月19日内,波动率开方是偏差变动绝对值的格兰杰原因,而在样本期2010年4月16日至2012年6月21日内,跳跃变动绝对值是偏差变动绝对值的格兰杰原因。
在基于SVCJ模型中,模糊性期货价格模型得到相似的结果。在样本期2010年4月16日至2011年9月1日内,波动率开方的滞后2期和滞后4期显著,波动率开方是偏差变动绝对值的格兰杰原因。在样本期2010年4月16日至2012年6月21日内,虽然不存在波动率开方的滞后项显著,但是跳跃变动绝对值的滞后4期在1%显著性水平下显著,且格兰杰因果检验显示跳跃变动绝对值是偏差变动绝对值的格兰杰原因。在样本期2010年4月16日至2014年12月19日内,波动率开方滞后3期和滞后4期显著,格兰杰因果检验的p值为0.000,波动率开方是偏差变动绝对值的格兰杰原因。跳跃变动绝对值的滞后4期在1%显著性水平下显著,且跳跃变动绝对值的格兰杰因果检验p值为0.039,因此跳跃变动绝对值也是偏差变动绝对值的格兰杰原因。因此,向量自回归结果支持模糊性期货定价模型。
6 模糊性的测度
为了更好地检验模糊性期货定价模型的有效性,下面对中国期货市场的模糊性进行测度。由模型推导可知,期货价格的边界满足以下随机过程
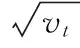
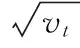
(36)
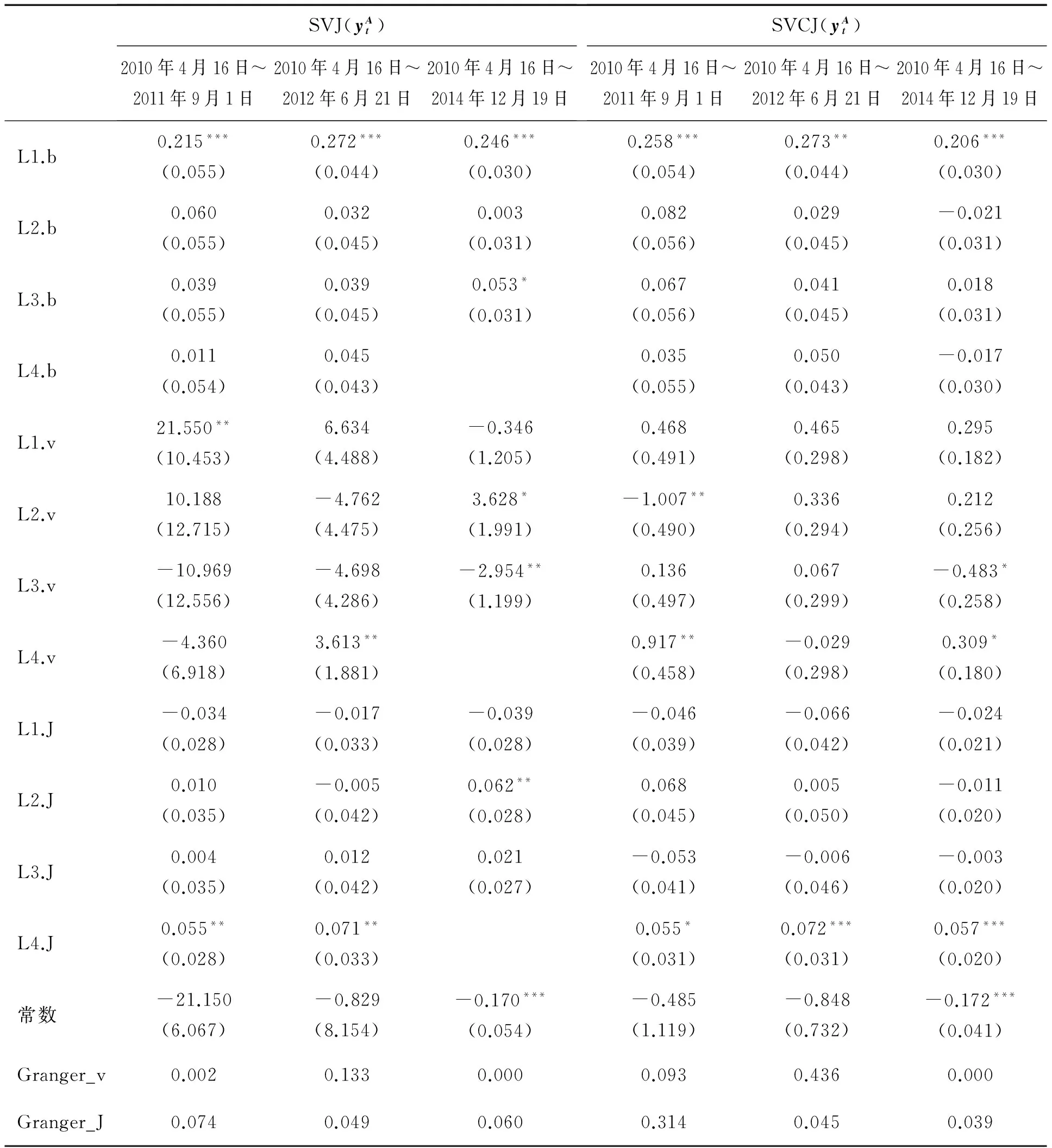
表5 基于SVJ和SVCJ模型的向量自回归分析Table 5 Vector Auto-Regression Analysis of SVJ and SVCJ Model
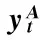
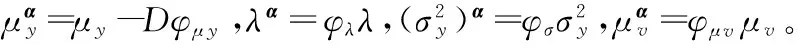
当参与期货市场的推动者为净股票持有者时,D=-1;当参与期货市场的推动者为净股票卖空者时,D=1。由于期货市场推动者数据难以获得,因此在本研究中选取股票上升和下降作为代理变量,即当St>St-1时D=-1,St 表6 模糊性的参数估计Table 6 Estimation of Ambiguity Parameter (36)式参数的估计结果见表6。若不考虑期货市场推动者头寸,假设市场中投资者均为净股票持有时,D=1,参数估计结果见表6中A。在不考虑期货市场推动者头寸时,φS和φv这两个依赖期货市场推动者头寸方向的系数在SV、SVJ和SVCJ这3个模型中均不显著,而同样依赖投资者方向的股票价格跳跃幅度均值φμy在SVCJ模型中也不显著。这有两个解释,一是中国期货市场模糊性不明显,二是股票资产净持有者和净卖空者交替推动期货交易,两者对期货价格产生的影响相互抵消。这两个解释对不受投资者持有资产方向影响的模糊性参数有不同影响,在第1种解释中不受投资者持有资产方向影响的模糊性参数应不显著,而在第2种解释中不受投资者持有资产方向影响的模糊性参数应显著。注意到φλ、φσ和φμv这3个不受资产持有方向影响的模糊性参数显著大于0,表明第2种解释更加符合中国期货市场特征。 考虑交易推动者的估算结果见表6中B情景,结果显示在考虑方向后,φS显著为正,这与模型预期一致。φv依然不显著,意味着对于投资者而言,波动率的布朗运动部分的模糊性并不明显。同样地,φλ、φσ和φμv这3个关于跳跃的参数显著为正,与表6中A情景一致。考虑期货价格偏差的方向性提高了参数估计的解释力度,进一步印证了存在双向偏差的模糊性期货定价模型能更好地刻画中国股指期货交易价格。 本研究在更具普遍意义的不确定性环境中讨论期货定价问题,从模糊性厌恶视角分析中国期货市场中出现的价格偏差现象,建立模糊环境中的投资者消费投资决策模型,推导得到模糊性期货理论价格,利用2010年至2014年中国股票指数和股指期货的交易数据对该期货价格模型进行实证检验。 研究结果表明,①在模糊性条件下,模糊性厌恶型投资者根据其资产头寸在概率测度集合中选取最稳健的概率测度测量未来结果。这种策略依赖型的概率测度选择方式导致在经济体中产生内生性意见分歧,从而使期货价格偏离了完美市场中的理论值,产生价格偏差。因此,股票指数和股指期货在持有期收益率和随机变动过程这两个方面并不等价,两者存在较大差异。②与随机利率期货模型相比,模糊性期货定价模型更符合中国实际经验,它能更好地解释中国股票指数波动率和股指期货价格偏差变动的动态关系。③定量分析表明,中国资本市场的模糊性在经济意义和统计意义上均显著,它是影响期货价格随机过程的一个重要因素。总体而言,模糊性期货定价模型更好地刻画了中国期货市场的交易现象,解释了中国期货市场出现的价格偏差现象。 模糊性期货定价模型重新解读了期货价格与基础资产之间的关系,对中国资本市场定价有以下启示。①模糊性包括了风险测度(基准概率测度)以及该测度的可信程度(概率测度集合中其他可能的测度)两个维度,因此,投资者在衍生品定价时除了分析基础资产的运行规律,还需考虑对基础资产运行规律估计的可信程度,对资产进行合理定价,避免出现较大的定价误差。②管理和对冲不确定性时,尤其是在使用衍生工具的情况下,金融机构应在模糊性框架下进行分析,合理安排衍生工具并有效管理其面临的不确定性程度。③由于模糊性程度决定期货定价偏差的幅度,因此,为避免衍生品价格的大幅度波动,监管部门应该对投资者进行有效的预期管理,降低市场模糊性。 本研究是模糊性期货定价的一个尝试,尚存在一些不足。其中一个值得继续深入探讨的话题是模糊性的决定因素问题,本研究为简单起见将模糊性外生为一个常系数进行分析,而事实上投资者面临的模糊性随着经济环境的变动而改变。在下一步的研究中,可以将模糊性作为经济体中的内生变量加以分析讨论。 [1]左浩苗,刘振涛,曾海为.基于高频数据的股指期货与现货市场波动溢出和信息传导研究[J].金融研究,2012(4):140-154. ZUO Haomiao,LIU Zhentao,ZENG Haiwei.Volatility spillover and information transmission in China′s stock index futures and spot markets:Empirical evidence from high frequency data[J].Journal of Financial Research,2012(4):140-154.(in Chinese) [2]郦金梁,雷曜,李树憬.市场深度、流动性和波动率:沪深300股票指数期货启动对现货市场的影响[J].金融研究,2012(6):124-138. LI Jinliang,LEI Yao,LI Shujing.Market depth,liquidity and price volatility:The launching of HS300 index futures and its impacts on the spot market[J].Journal of Financial Research,2012(6):124-138.(in Chinese) [3]乔高秀,刘强.沪深300股指期货定价偏差影响因素及非线性调整特征[J].投资研究,2013,32(10):83-97. QIAO Gaoxiu,LIU Qiang.Influential factors and nonlinear adjusting feature for the CSI 300 index futures mispricing[J].Review of Investment Studies,2013,32(10):83-97.(in Chinese) [4]魏卓,陈冲,魏先华.基于高频数据的中国市场股指期货套利[J].系统工程理论与实践,2012,32(3):476-482. WEI Zhuo,CHEN Chong,WEI Xianhua.Chinese stock index futures arbitrage based on high-frequency data[J].Systems Engineering-Theory & Practice,2012,32(3):476-482.(in Chinese) [5]MCMILLAN D G,ÜLKÜ N.Persistent mispricing in a recently opened emerging index futures market:Arbitrageurs invited[J].The Journal of Futures Markets,2009,29(3):218-243. [6]CUMMINGS J R,FRINO A.Index arbitrage and the pricing relationship between Australian stock index futures and their underlying shares[J].Accounting & Finance,2011,51(3):661-683. [7]马理,卢烨婷.沪深300股指期货期现套利的可行性研究:基于统计套利模型的实证[J].财贸研究,2011,22(1):88-93. MA Li,LU Yeting.Feasibility study on arbitrage of CSI-300 stock index futures:Empirical research based on statistical arbitrage model[J].Finance and Trade Research,2011,22(1):88-93.(in Chinese) [8]徐国祥,刘新姬.沪深300股指期货定价模型的改进及实证研究[J].统计与信息论坛,2012,27(2):54-61. XU Guoxiang,LIU Xinji.Improved pricing model of Hushen300 stock index futures and empirical research[J].Statistics & Information Forum,2012,27(2):54-61.(in Chinese) [9]CORNELL B,FRENCH K R.The pricing of stock index futures[J].Journal of Futures Markets,1983,3(1):1-14. [10] KLEMKOSKY R C,LEE J H.The intraday ex post and ex ante profitability of index arbitrage[J].Journal of Futures Markets,1991,11(3):291-311. [11] MACKINLAY A C,RAMASWAMY K.Index-futures arbitrage and the behavior of stock index futures prices[J].The Review of Financial Studies,1988,1(2):137-158. [12] HEMLER M L,LONGSTAFF F A.General equilibrium stock index futures prices:Theory and empirical evidence[J].Journal of Financial and Quantitative Analysis,1991,26(3):287-308. [13] KNIGHT F H.Risk,uncertainty and profit[M].Boston,MA:Houghton Mifflin Company,1921:197. [14] ELLSBERG D.Risk,ambiguity,and the savage axioms[J].The Quarterly Journal of Economics,1961,75(4):643-669. [15] HANSEN L P,SARGENT T J.Robust control and model uncertainty[J].The American Economic Review,2001,91(2):60-66. [16] HANSEN L P,SARGENT T J,TURNUHAMBETOVA G,et al.Robust control and model misspecification[J].Journal of Economic Theory,2006,128(1):45-90. [17] TIAN W,WANG T.Asset pricing under uncertainty:No-arbitrage approach[R].Charlotte:University of North Carolina at Charlotte,2010. [18] POLKOVNICHENKO V.Ambiguity aversion and the arbitrage pricing theory[R].Irving,Texas:University of Texas at Dallas,2010. [19] 高金窑.奈特不确定性与非流动资产定价:理论与实证[J].经济研究,2013,48(10):82-97. GAO Jinyao.Illiquid asset pricing under Knightian uncertainty:Theory and evidence[J].Economic Research Journal,2013,48(10):82-97.(in Chinese) [20] DOW J,DA COSTA WERLANG S R.Excess volatility of stock prices and Knightian uncertainty[J]. European Economic Review,1992,36(2/3):631-638. [21] CAO H H,WANG T,ZHANG H H.Model uncertainty,limited market participation,and asset prices[J].The Review of Financial Studies,2005,18(4):1219-1251. [22] EPSTEIN L G,WANG T.Intertemporal asset pricing under Knightian uncertainty[J].Econometrica,1994,62(2):283-322. [23] GUIDOLIN M,RINALDI F.Ambiguity in asset pricing and portfolio choice:A review of the literature[J].Theory and Decision,2013,74(2):183-217. [24] ETNER J,JELEVA M,TALLON J M.Decision theory under ambiguity[J].Journal of Economic Surveys,2012,26(2):234-270. [25] GAGLIARDINI P,PORCHIA P,TROJANI F.Ambiguity aversion and the term structure of interest rates[J].The Review of Financial Studies,2009,22(10):4157-4188. [26] DRECHSLER I.Uncertainty,time-varying fear,and asset prices[J].The Journal of Finance,2013,68(5):1843-1889. [27] LIU J,PAN J,WANG T.An equilibrium model of rare-event premia and its implication for option smirks[J].The Review of Financial Studies,2005,18(1):131-164. [28] FARIA G,CORREIA-DA-SILVA J.A closed-form solution for options with ambiguity about stochastic volatility[J].Review of Derivatives Research,2014,17(2):125-159. [29] EPSTEIN L G,JI S.Ambiguous volatility and asset pricing in continuous time[J].The Review of Financial Studies,2013,26(7):1740-1786. [30] BAUM C F,WAN C.Macroeconomic uncertainty and credit default swap spreads[J].Applied Financial Economics,2010,20(15):1163-1171. [31] GUO L.Determinants of credit spreads:The role of ambiguity and information uncertainty[J].The North American Journal of Economics and Finance,2013,24(C):279-297. [32] LIEN D.Production and hedging under Knightian uncertainty[J].Journal of Futures Markets,2000,20(4):397-404. [33] LIEN D,WANG Y.Futures market equilibrium under Knightian uncertainty[J].Journal of Futures Markets,2003,23(7):701-718. [34] RAO V K.Hedging,speculation and forward market equilibrium under ambiguity[R].Minnesota:Metropolitan State University,2015. [35] WONG K P.Ambiguity and the value of hedging[J].Journal of Futures Markets,2015,35(9):839-848. [36] BOYARCHENKO N.Ambiguity shifts and the 2007-2008 financial crisis[J].Journal of Monetary Economics,2012,59(5):493-507. [37] JEONG D,KIM H,PARK J Y.Does ambiguity matter?Estimating asset pricing models with a multiple-priors recursive utility[J].Journal of Financial Economics,2015,115(2):361-382. [38] GILBOA I,SCHMEIDLER D.Maxmin expected utility with non-unique prior[J].Journal of Mathematical Economics,1989,18(2):141-153. [39] CHEN Z,EPSTEIN L.Ambiguity,risk,and asset returns in continuous time[J].Econometrica,2002,70(4):1403-1443. [40] 吴卫星,付晓敏.信心比黄金更重要?关于投资者不确定性感受和资产价格的理论分析[J].经济研究,2011,46(12):32-44. WU Weixing,FU Xiaomin.Confidence is more valuable than money:A theoretical analysis on investors′ attitudes toward uncertainty and asset prices[J].Economic Research Journal,2011,46(12):32-44.(in Chinese) [41] BATES D S.Jumps and stochastic volatility:Exchange rate processes implicit in deutsche mark options[J].The Review of Financial Studies,1996,9(1):69-107. [42] ERAKER B,JOHANNES M,POLSON N.The impact of jumps in volatility and returns[J].The Journal of Finance,2003,58(3):1269-1300. [43] HESTON S L.A closed-form solution for options with stochastic volatility with applications to bond and currency options[J].The Review of Financial Studies,1993,6(2):327-343. [44] GARLAPPI L,UPPAL R,WANG T.Portfolio selection with parameter and model uncertainty:A multi-prior approach[J].The Review of Financial Studies,2007,20(1):41-81. [45] EPSTEIN L G,SCHNEIDER M.Recursive multiple-priors[J].Journal of Economic Theory,2003,113(1):1-31. [46] LI H,WELLS M T,YU C L.A Bayesian analysis of return dynamics with lévy jumps[J].The Review of Financial Studies,2008,21(5):2345-2378. [47] 乔高秀,刘强,张茂军.沪深 300 股指期货上市对现货市场连续波动和跳跃波动的影响[J].中国管理科学,2014,22(10):9-18. QIAO Gaoxiu,LIU Qiang,ZHANG Maojun.The impacts of CSI 300 index futures on the continuous volatility and jump volatility of the cash market in China[J].Chinese Journal of Management Science,2014,22(10):9-18.(in Chinese) [48] BAI J,PERRON P.Computation and analysis of multiple structural change models[J].Journal of Applied Econometrics,2003,18(1):1-22. TheStudyofAmbiguityandStockIndexFuturePricesBidirectionalDeviation FENG Ruimin,LU Jialiu Business School, Sun Yat-sen University, Guangzhou 510275, China CSI 300 stock index futures pricing shows a special pattern: the mispricing in the future market is bidirectional, and most of time is positive. This pattern is quite different from that in the foreign financial market, since it is more often to witness negative mispricing in foreign future markets. What′s worse, this pattern cannot be explained by the current stock-index futures pricing model. In order to explain this phenomenon, this paper builds up a new future pricing model from the perspective of ambiguity.We first build up the continuous infinite life consumption-investment model of ambiguity-averse investors to study their optimal decisions under ambiguity circumstance. We investigate the relationship between investors′ asset position and the equilibrium asset prices, proposing the ambiguity future pricing model. After that, based on CSI 300 stock index′s and its future′s daily data from 2010-2014, the new pricing model is tested. Both Monte Carlo Markov Chain estimation method and vector auto-regression tests are adopted. Finally, we calibrate the ambiguity parameter in Chinese financial market. Our study provides the following findings. First and foremost, future′s stochastic process deviates from its underlying under ambiguous circumstances. The non-arbitrage mechanism cannot ensure that the future′s price follows the same process of the index. Meanwhile, investors won't change their investment strategy if future′s price is within the ambiguous pricing range. Secondly, the direction of the mispricing is determined by the net asset position of the transaction-driven investors. Under the assumption of ambiguity, ambiguity-averse investor's preserved price of the future is affected by his asset position. Hence, if the future transaction is driven by those in the net long position, there is a positive mispricing of the future price. Otherwise, the negative mispricing exists if it is driven by those in the net short position. Thirdly, the degree of mispricing is determined by how severe the ambiguity investors face. The potential future price range is derived given the probability set, that is, the ambiguity environment. The severer ambiguity investors face, the larger the potential future price ranges. Moreover, the empirical data from Chinese market supports the new pricing model. The dynamics relation between volatility and future mispricing under classical future pricing model, the stochastic-interest future pricing model and the ambiguity future pricing model are different. The Vector Auto-Regression and Granger causality only supports the relations implied by the ambiguity pricing model. Last but not the least, the ambiguity is statistically and economically significant in Chinese financial market. In short, future pricing model shows a different pricing pattern with consideration of ambiguity. And empirical tests provide evidences that ambiguity plays a role in Chinese future market. Hence ambiguity should be taken into consideration in further asset pricing study. ambiguity;stock index futures;futures pricing;mispricing;positive devation Date:April 1st, 2015 DateAugust 28th, 2015 Biography:FENG Ruimin (1988-,Native of Guangzhou, Guangdong), is a Ph.D candidate in Business School at Sun Yat-sen University. Her research interests cover asset pricing and capital market, etc. E-mail:qingfenglitiaotiao@126.com F830.9 A 10.3969/j.issn.1672-0334.2015.06.009 1672-0334(2015)06-0105-17 2015-04-01修返日期2015-08-28 冯瑞敏(1988-),女,广东广州人,中山大学管理学院博士研究生,研究方向:资产定价和资本市场等。 E-mail:qingfenglitiaotiao@126.com □
7 结论
