一个高效实现灰色关联分析的R程序

高志华++李桂琴++石晓辉++马莉丽

摘 要：灰色关联分析模型是一种广泛应用于各个科研领域的重要的统计模型，但其数据处理过程计算量很大。R是一门高级统计计算编程语言，可以在通用公共许可（GPL）规则下从互联网免费获取。该研究基于灰色关联分析方法设计了一个可快速自动计算邓氏关联度的R程序，通过成功应用于实例，验证了本程序的可行性和高效性。

关键词：R语言；灰色关联分析；R程序应用实例

中图分类号 N941.5 文献标识码 A 文章编号 1007-7731（2015）23-13-04

An Efficient R Program for Implementing Grey Relational Analysis

Gao Zhihua1，2，3 et al.

（1College of Biological Science and Engineering，Hebei University of Economics and Business，Shijiazhuang 050061，China；2 School of Life Science，Hebei Normal University，Shijiazhuang 050016，China；3 School of Life Sciences，Fudan University，Shanghai 200438，China）

Abstract：Grey relational analysis model widely used in various scientific research fields is a very important statistical model，but it needs lots of computations to finish the whole data process. R is an advanced programming language for statistical computing and is available as free software downloaded from the Internet under the terms of the Free Software Foundations GNU General Public License.In this paper，based on the method of grey relational analysis，a fast automatic calculation program in R for Deng relational degree is designed，and successfully applied into the actual case to verify its feasibility and high-efficiency.

Key words：R program；Grey relational analysis；Application case in R program

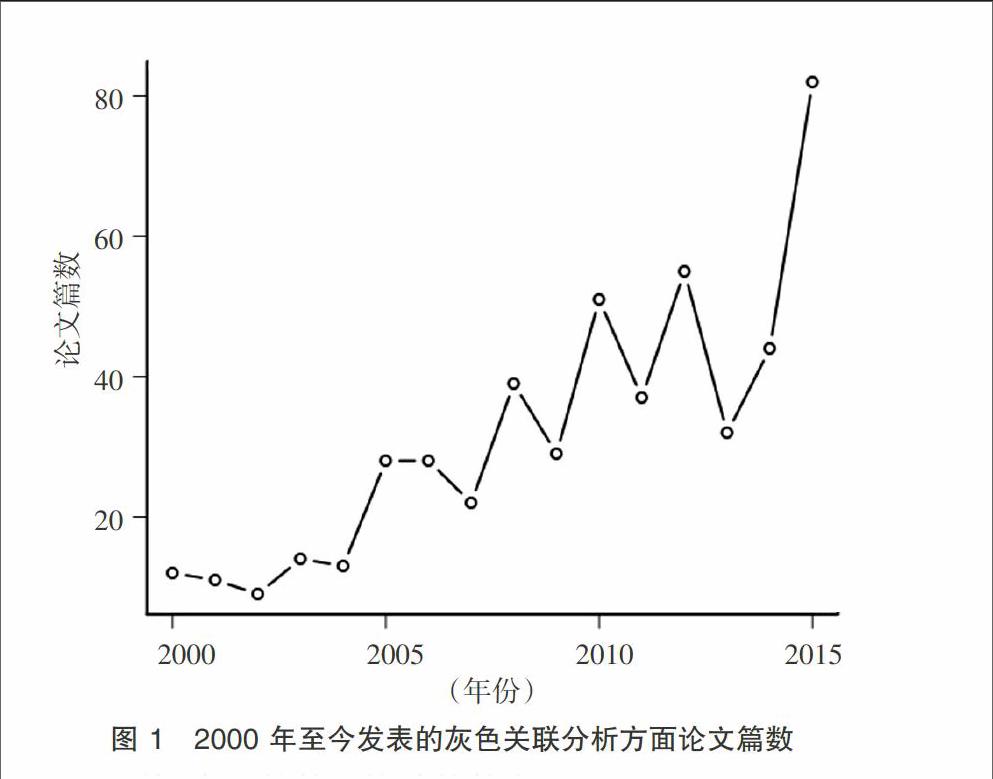
灰色关联分析是从无序、随机的系统特征量中确定各因素间的关联程度，早在1982年，邓聚龙教授就提出了计算灰色关联度的统计模型，该模型基本思想是根据序列曲线几何形状的相似程度来判断其联系是否密切，曲线越接近，则相应序列之间关联度就越大，反之则越小[1-3]。灰色关联分析方法是处理“小样本”、“贫信息”不确定系统的有效方法，因其实用性强，且不像其他多元统计模型（如相关、回归等）要求大样本和符合典型分布，故在许多科学研究领域都用广泛应用[4]。经初步统计中国知网文献检索结果，发现从2000年至今，公开发表的应用灰色关联分析模型解决生命科学问题的相关学术论文已有506篇，且大体呈上升趋势（如图1所示），可见，灰色关联分析方法在生命科学领域的应用日益广泛。

图1 2000年至今发表的灰色关联分析方面论文篇数

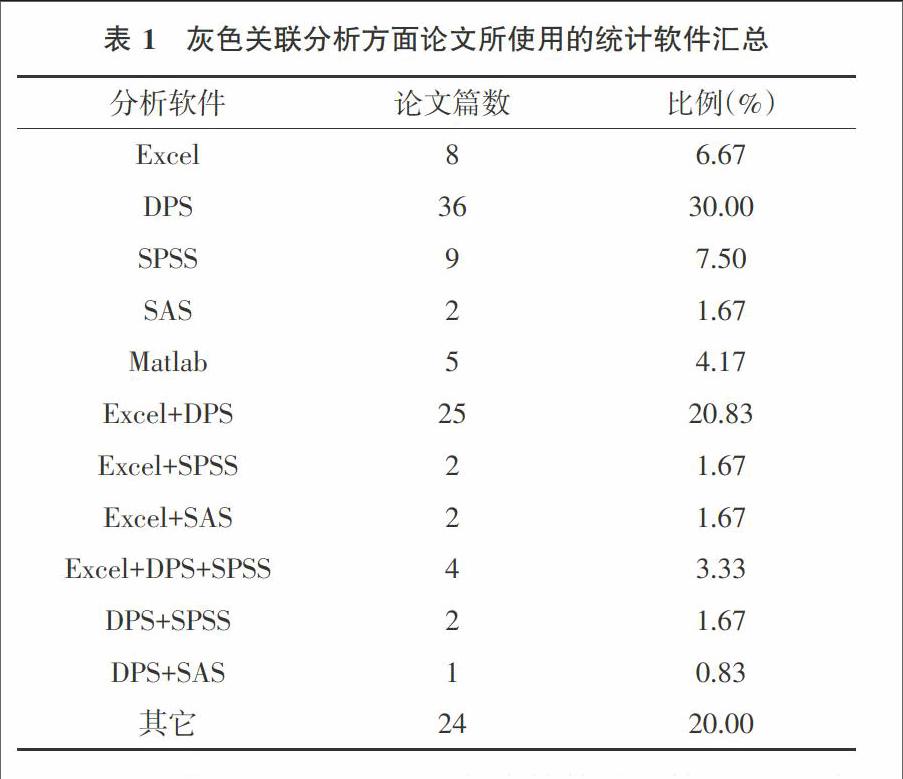
目前，常用的数理统计软件有：Excel、SPSS、SAS、DPS等[5，6]。在这506篇论文中有120篇明确指出了灰色关联分析所使用的数据分析软件，但是所使用的软件种类却不尽相同（见表1）。

Excel是Microsoft Office办公软件的组件之一，具有数据统计分析的功能，比较灵活、直观，能够根据不同计算目的，编写不同的公式来进行一些简单的数据分析，有6.67%的灰色关联分析单独使用Excel来完成，有27.5%的灰色关联分析需要Excel配合其它软件来完成，说明Excel在日常数据分析中占有重要地位，但是，如果使用Excel处理大量数据，即使是使用相同算法，也需要每次输入众多数学公式，进行繁琐的代数运算，费时费力，还易出错；SPSS和SAS都是非常优秀的国外数理统计软件，它们区别在于：前者已经将常用的统计算法固化于软件之中，只要熟练掌握使用方法，能够减少重复性劳动，且分析效率高，但由于其自身封闭性，如果想使用一些不常用或最新的算法处理自己的数据，则不支持，除非软件编制者更新这些算法，后者除了具备各种统计功能之外，还能够通过编程来实现自己的特殊算法，以满足不同的数据处理需求，但是，要求使用者事先熟练掌握其复杂的编程语法，由于二者都要求使用者事先熟练掌握大量的功能函数及相应分析模型的理论，而且都是英文操作界面，这就使得基础科技工作者难以在短期内准确掌握；Matlab已经发展为综合高性能的数值计算软件，在数理统计方面的功能不断增强，也支持编程，情况与SAS类似[7]；DPS（Data Processing System）是由浙江大学农业与生物技术学院唐启义教授研发的国内首款中文操作界面数理统计软件，因其无需使用者了解具体运算细节，仅靠点击鼠标即可完成绝大多数的数据分析任务，简单易行，所以越来越得到广大科技工作者的认可[8]。与SPSS、SAS和Matlab的22.5%使用率相比，有56.67%的学者选择DPS进行灰色关联分析也充分说明了这一点。但值得一提的是，无论是与SPSS、SAS、Matlab，还是DPS，都属于商业软件，有的甚至还需要二次支付额外费用才能使用这些软件的某些数理统计模块，无疑给科研工作增加了不小的成本投入。也正是基于这一点，本文首次探索R语言实现灰色关联分析的新途径。

1 R语言简介

R语言是一门出色的统计计算编程语言，属于解释性计算机语言，可以在通用公共许可（GPL）规则下从互联网免费获取，能够将其部署在Microsoft Windows、UNIX、Linux以及Macintosh OS X系统中，可以实现“一次编码，到处运行”，极大提高了分析效率[9]。R语言为统计建模和图示提供了种类繁多、唾手可得的软件包，还允许用户既可以使用成熟的统计技术，也可以使用实验性的统计技术。同时，R语言具有极其丰富的绘图功能，如前文图1就是使用ggpolt2 R包绘制。与C/C++语言相比，R语言是一种更加高级的编程语言，易学易用，尽管其执行速度稍逊，但实践表明，其开发速度带来的效益远远大于执行速度带来的损失，特别是在现代计算机的处理速度情况下。R语言现已逐步成为国内外众多科技工作者青睐的数据分析工具。

2 邓氏灰色关联分析算法简介及R实现

灰色关联分析方法依据空间理论的数学基础，按照规范性、偶对称性、整体性和接近性的灰色关联四原则，以确定参考序列和若干个比较序列之间的关联系数和关联度。邓氏关联分析模型是最早运用灰色系统理论计算灰色关联度的统计模型，在各个学科领域均有应用，所以寻求一种简单、自动、高效的邓氏关联度计算方法十分必要。

2.1 邓氏灰色关联分析算法 邓氏灰色关联分析模型包括以下6个计算步骤：

（1）确定待分析的变量序列。参考序列用x0表示，比较序列用xi（i=1，2，…，n，表示共有n个比较序列）表示，统称为变量序列[4]。

（2）对变量序列进行无量纲化。为了消除各指标量纲不一致对关联分析的影响，要在分析前对变量序列原始数据进行无量纲化处理，处理后的参考序列用x′0表示，比较序列用x′i（i=1，2，…，n，表示共有n个比较序列）表示。常用的方法有初值化法、均值化法、区间化法、逆化法、倒数化法等[10-11]。

（3）求差序列、最大差和最小差。根据公式：△0i（k）=|x′0（k）-x′i（k）|（其中，i=1，2，…，n，表示共有n个比较序列；k=1，2，…，m，表示每个比较序列由m个指标组成）计算参考序列与其余各比较序列的绝对差值，并找出其中的最大差和最小差，分别用△max与△min表示。

（4）计算关联系数。其中，为关联系数，ρ为分辨系数，0≤ρ≤1，一般ρ取0.5。

（5）计算关联度。其中，为参考序列x0与比较序列xi的邓氏关联度，为第k个指标的加权系数。

（6）按取值大小进行排序。对各从大到小进行排序，取值越大，说明比较序列与参考序列的平均距离越小，越相似。

2.2 邓氏灰色关联分析算法的R实现及要求 利用R软件（V3.20）编程实现上述算法，该程序提供了初值化和均值化两种变量序列无量纲化方法，及是否加权计算邓氏关联度的选项，运行该程序的基本环境要求如下：（1）硬件要求：目前主流的个人电脑配置（32位或64位）均可，一般硬盘最好40GB以上，内存最好2GB以上。（2）软件要求：安装WindowXP或Windows 7操作系统，安装2003及以上Microsoft Office办公软件，安装V3.20及以上R环境。

3 R程序应用于实例

以灰度关联分析方法对不同南瓜品种的产量和果胶质量（果胶含量、酯化度、粘度）进行综合评价为例[12]，使用上述R程序进行灰度关联分析过程如下：

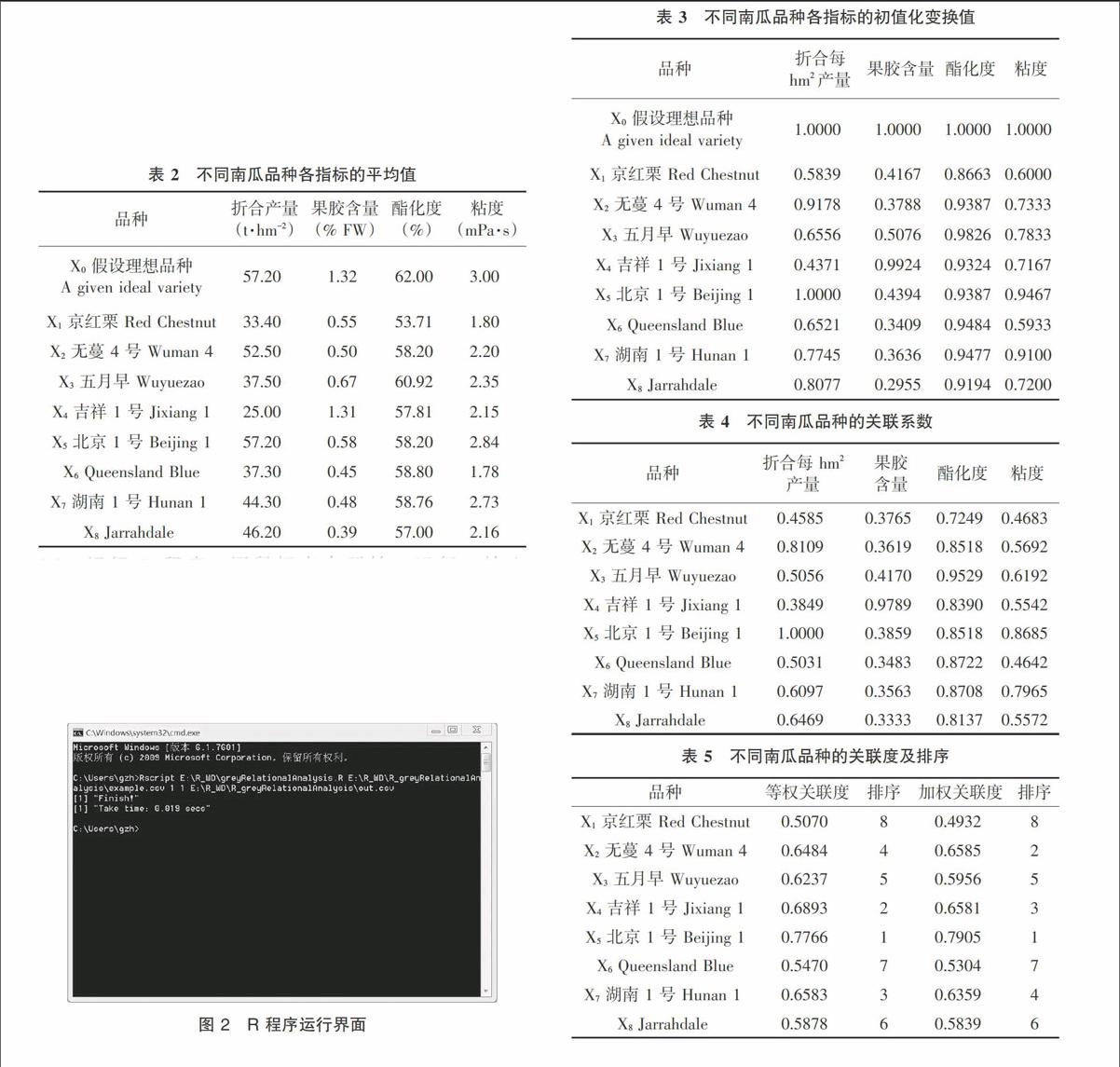
3.1 新建原始数据文件 新建原始数据文件example.csv，键入不同南瓜品种的产量和果胶质量（果胶含量、酯化度、粘度）的原始数据（见表2），保存并退出。

在上述命令中，greyRelationalAnalysis.R为邓氏灰色关联分析R程序，example.csv为原始数据文件，接下来的2个“1”分别是无量纲化方法参数和是否加权参数，out.csv为分析结果文件。在此，无量纲化方法参数共有2个：1表示初值化法，2表示均值化法；是否加权参数也有两个：0表示不加权，1表示加权。

3.3 分析结果 采用初值化法将9种南瓜品种（含假设理想品种）各指标的平均值进行无量纲化后，得到如表3所示结果；再将8种南瓜品种分别与假设理想品种做比较，得到8种南瓜品种与假设理想品种间各指标的关联系数（见表4）；然后按照加权（各指标的权重依次为：0.35、0.25、0.20、0.20）和不加权两种方式计算8种南瓜品种与假设理想品种间邓氏关联度；最后对两类关联度分别进行排序（见表5）。

由表5可知，不论是加权还是不加权，北京1号的邓氏关联度最高，京红栗的邓氏关联度最低，根据灰色系统理论，北京1号不仅产量高，而且果胶品质好，适宜用于果胶开发，京红栗不宜作果胶开发原料，这与苏艳玲等[12]的分析结果一致，说明本文开发的R程序可以进行邓氏灰色关联分析。

4 讨论与结论

根据研究对象的不同特征，除邓氏灰色关联分析模型外[13]，还有灰色绝对关联度、相对关联度、广义关联度[14-16]、灰色斜率关联度、区间关联度Ⅰ[17]、点关联度、区间关联度Ⅱ[18]、B型关联度、C型关联度[19]、T型关联度[20]、向量关联度、复数关联度[21]等。SPSS和DPS是十分成熟的软件，但很难涵盖上述所有灰色关联分析模型；SAS和Matlab除了提供各种统计功能，还支持编程，但由于和SPSS、DPS一样，只有付费才能获得正版软件的使用权，增加了广大科技工作者的科研成本；Excel生动直观，但计算繁琐且容易出错。R软件是一款自由、免费、开源的软件，具有强大的统计分析功能，同时又是一门高级编程语言，而且无需编译过程，开发周期较短，代码维护方便，程序运行简单。本文根据邓氏灰色关联分析算法编写的R程序分析了不同南瓜品种的产量和果胶质量（果胶含量、酯化度、粘度）各指标，得到了与苏艳玲等[12]一致的分析结果，并且从原始数据输入到分析任务完成仅用0.019秒（见图2），可见本程序对灰色关联分析的可行性和高效性，同样，本程序也非常适合大量数据的分析和重复性强的工作。通过利用R编程对邓氏关联分析的成功探索，为日后继续开发其它灰色关联分析模型的R程序奠定了坚实基础。

参考文献

[1]邓聚龙.灰色系统基础方法[M].武汉：华中理工大学出版社，1987.

[2]李东亮，冯广林，李刚，等.灰色系统理论在烟草质量评价中的应用[M].北京：中国水利水电出版社，2013.

[3]刘思峰，谢乃明.灰色系统理论及其应用[M].北京：科学出版社，2013.

[4]谭学瑞，邓聚龙.灰色关联分析：多因素统计分析新方法[J].统计研究，1995，65（3）：46-48.

[5]朱海涛，陈黎，涂自良，等.DPS数据处理系统在药学研究数据处理中的应用[J].医药导报，2006，25（4）：363-365.

[6]唐启义，冯明光.DPS数据处理系统——实验设计、统计分析及模型优化[M].北京：科学出版社，2006.

[7]周建兴，岂兴明，矫津毅，等.MATLAB从入门到精通[M].北京：人民邮电出版社，2012.

[8]唐启义.通用统计软件DPS研制与应用[J].科学中国人，2004（9）：56.

[9]郝智恒，何通，邓一硕，等.R语言统计入门（第2版）[M].北京：人民邮电出版社，2014.

[10]徐文凤，毛志泉，孙海涛，等.灰色关联度分析法在拮抗丝核菌木霉菌株筛选中的应用[J].山东农业大学学报，2012，43（2）：189-192.

[11]刘新梅，徐润芳，张若勇.邓氏灰色关联分析的应用模型[J].统计与决策，2008，262（20）：23-25.

[12]苏艳玲，张学杰.不同南瓜品种果胶含量与特性分析及其利用评价[J].园艺学报，2014，41（11）：2323-2328.

[13]邓聚龙.灰色系统理论教程[M].武汉：华中理工大学出版社，1990.

[14]刘思峰，党耀国，方志耕.灰色系统理论及其应用[M].北京：科学出版社，2010.

[15]XIE N M，LIU S F.Research on evaluations of several grey relational models adapt to grey relational axioms[J].Journal of Systems Engineering and Electronics，2009，20（ 2）：304-309.

[16]GU H，SONG B F.Study on effectiveness evaluation of weapon systems based on grey relational analysis and TOPSIS[J].Journal of Systems Engineering and Electronics，2009，20（1）：106-111.

[17]崔杰，党耀国，刘思峰.几类关联分析模型的新性质[J].系统工程，2009，27（4）：65-70.

[18]肖新平，宋中民，李峰.灰技术基础及其应用[M].北京：科学出版社，2005.

[19]王清印.灰色B型关联度分析[J].华中理工大学学报，1989，17（6）：77-81.

[20]唐五湘.T型关联度及其计算方法[J].数理统计与管理，1995，14（1）：34-37.

[21]谢乃明，刘思峰.积累关联度模型的平行性和一致性[J].系统工程，2007，25（8）：98-103.

（责编：张长青）