非对称直线-余弦-直线运动规律及其在经编机中的应用
2015-12-25钱永明
钱永明
(南通大学机械工程学院,江苏南通 226019)
在多梳栉经编机成圈运动装置中,复合针的上下运动和摆动、压纱运动等大都采用凸轮-连杆组合机构[1-2],由其中的凸轮机构实现各成圈机件的复杂运动要求,从而使凸轮设计成为研发经编机新机型的关键任务。选用合适的凸轮机构从动件运动规律是设计凸轮轮廓线的基础,主要从2个方面考虑:一是运动位移变化要求的特点;二是边界条件。对于成圈机构,成圈机件的运动位移变化要求比较复杂,另外,为有利于提高整机转速,边界条件一般取U-U型,即在起始点和终点无停留立即反向。适用于U-U型边界条件的运动规律一般为对称型结构,如对称型余弦加速度、余弦-直线-余弦、直线-余弦-直线等[3],都不能满足成圈机件运动位移的复杂变化要求。实际产品开发效果表明,非对称型组合运动规律能较好地满足成圈机件运动要求比较复杂的情况,考虑到跃度变化的连续性,本文选用非对称直线-余弦-直线型运动规律。
组合型运动规律的研究方法有运动参数直接推导法[4-6]、通用方程法[3]等,前者针对性强,计算程序简单,应用便捷。后者通用性好,但分析过程、计算程序复杂,根据加速度组成,有按照 7 段[7-8]、9 段[9]、15 段[10]分别计算各段的位移、速度、加速度和跃度变化规律,分段越多,分析和计算越复杂。根据经编机产品开发针对性强的应用特点,本文采用运动参数直接推导法分析非对称直线-余弦-直线型运动规律。
1 运动方程
非对称直线-余弦-直线运动规律由3段构成,如图1所示。图中φ为凸轮转角,a为从动件运动加速度。第1段和第3段分别为直线,第2段为余弦,对应凸轮转角分别为 φ1、φ2和 φ3。设加速度的正、负幅值的绝对值分别为Ca和Ca1,并设当λ=1时,为对称型直线-余弦-直线运动规律;当λ≠1时,即为非对称型直线-余弦-直线运动规律,并以对称线S为基准,横坐标φ到对称线S的距离称为偏移量y。
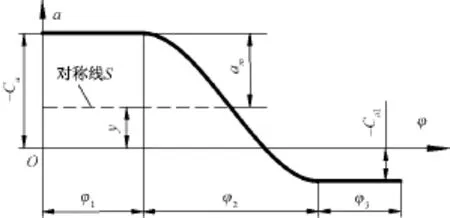
图1 由3段构成的加速度曲线Fig.1 Acceleration curve of three sections

式中0≤φ≤φ1。对应于第1段末端的边界条件
第2段,设Ca和Ca1的平均值为,则偏移量为

该段的加速度a、速度v和位移s分别为
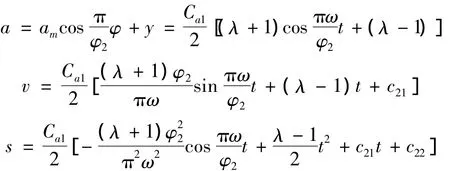
式中,c21和c22分别为积分常数。由边界条件:t=,代入上式,得c21=,所以,第2段的运动方程为

式中φ的变化范围为0≤φ≤φ2。对应于第2段的末端边界条件为:
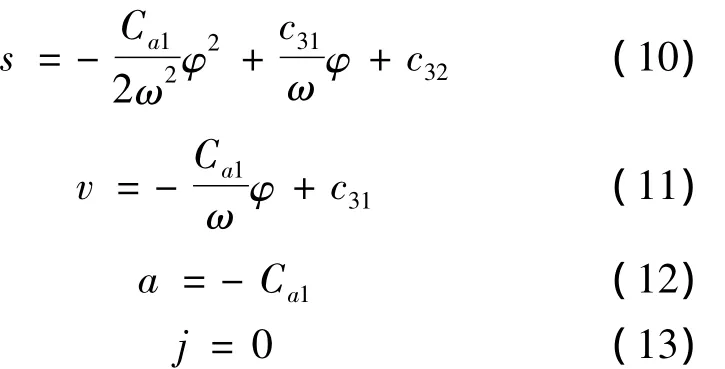
式中,φ的变化范围为0≤φ≤φ3。
设从动件的运动动程为h,则当φ=φ3时,s=h,v=0,代入式(10)和(11),得

采用该规律运动时,先根据需要将总的凸轮转角大小进行划分,即确定3段的凸轮转角φ1、φ2和φ3的值,由式(14)计算得到λ,再由式(15)计算得到Ca1,以及Ca= λCa1,最终由式(1)~(4)、(6)~(9)和式(10)~(13)可计算出各段的运动方程,将3段的运动拼接在一起构成整个过程的运动。
2 经编机槽针运动的应用
图2示出多梳栉压纱板经编机槽针、导纱针和沉降等成圈机件之间的运动关系。图中,1为复合针中的槽针,2为沉降(片),S1,S2,…,S11为从机器侧面投影梳栉工作线,Y为压纱板。
多梳栉经编机的复合针有沿机器前后方向(针床)摆动(机前和机后方向如图2中所示),也称前后运动,及垂直方向的上下运动,因此,槽针的运动是前后摆动和上下运动的复合运动,槽针针尖的运动轨迹为图2中所示的L1或L2曲线。槽针针尖运动轨迹分为上升段和下降段。一般情况下,槽针上升到最高位置时,针床摆动到达最前位置,则图2(a)中所示P点既是槽针运动的最高点,也是其运动最前点。设点P0为槽针运动最低点,槽针针尖由点P0按图2(a)中所示向上箭头上升、向前摆动,直至点P,这一过程称为槽针上升阶段和向前摆动阶段;由点P按向下箭头下降、向后摆动,这一过程称为槽针下降阶段和向后摆动阶段。

图2 多梳栉压纱板经编机槽针运动轨迹Fig.2 Motion traces of groove pin in multi-bar warp knitting machine.(a)Asymmetric line-cosine-straight motion trace of groove pin;(b)Asymmetric cosine motion trace of groove pin
前后运动由针床摆动机构实现,上下运动由槽针上下运动机构实现。槽针上下运动机构一般是凸轮-连杆组合机构[1-2],凸轮是主动件,利用非对称直线-余弦-直线运动规律实现上升段槽针针尖运动轨迹形状。
非对称余弦加速度运动规律的起始点和终点加速度均不等于0,适用于上升-返回型、在始末端无休止地立即反向的应用场合,多梳经编机中的槽针、针芯和针床摆动的运动边界条件都符合这类特点,所以,在设计这类成圈机件的凸轮运动机构时常选用该运动规律,并通过适当的运动规律偏移(即非对称余弦加速度运动规律),满足成圈机件具体运动要求。
为进行比较,选用非对称余弦加速度作为槽针上升段的运动规律,在保证槽针针尖运动轨迹与上述选定的非对称直线-余弦-直线运动规律相同或近似的前提下,比较2种运动规律对经编机成圈或动力学特性的影响。在本例中,按照多梳栉经编机编织工艺要求,取上升段凸轮转角φ=170.8°,从动件摆动范围角13.56°。对于非对称直线-余弦-直线运动规律,分配3段对应凸轮转角分别为:φ1=5°、φ2=70.8°和 φ3=95°,由式(14)计算得到λ =3.23,再由式(15),Ca1=4.18 s-2,以及 Ca=λCa1=13.51 s-2,由式(5),加速度偏移量 y=将计算的各项参数分别代入到式(1)~(4)、式(6)~(9)和式(11)~(13),求得槽针上下运动凸轮上升段的运动位移S、速度v、加速度a和跃度j。图3示出了位移、加速度和跃度曲线。图中横坐标φ为凸轮转角;从动件的运动形式为摆动。图2(a)中L1为在一定前后摆动的情况下相应槽针针尖运动轨迹。

图3 经编机槽针上升段运动曲线Fig.3 Increasing motion section curves of groove pin in warp knitting machine.(a)Displacement curve;(b)Velocity curve;(c)Jerk curve
3 比较与分析
3.1 轨迹形状
图4示出2种运动规律槽针针尖轨迹的对比情况。若保证2种运动规律槽针由最低点开始上升段的高度C基本一致,但在后续上升直至最高位置过程中,L2的高度略低于L1,最大距离约为0.98 mm。根据经编工艺,上升段轨迹太低会影响退圈效果,及针背垫纱效果。
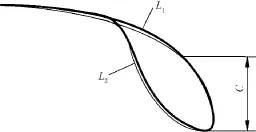
图4 2种轨迹对比Fig.4 Comparison of two traces
3.2 加速度和跃度
由上述计算及图3(b)、(c)可知,2种运动规律的加速度及跃度情况如下。
对非对称直线-余弦-直线:加速度极值 Ca为13.51 s-2,跃度极值 j为 22.53 s-3;
非对称余弦:加速度极值 Ca为16.2 s-2,跃度极值 j为 36.45 s-3。
对非对称直线-余弦-直线运动规律的加速度和跃度极值比本文选定的非对称余弦运动规律的加速度和跃度极值小,在本算例中,前者比后者的加速度极值减小了,跃度极值减小了较小的加速度极值会减小运动时的惯性力,而较小的跃度极值表示惯性力变化也较小。显然,对提升机器运转速度有利。另外,由图3(c)可看出,非对称直线-余弦-直线运动规律的跃度曲线连续,而非对称余弦加速度运动规律的跃度曲线在其中的一个点有突变,表示机器在运转过程中到达该位置时会有冲击,也不利于提升机器运转速度。
4 结语
通过调整非对称直线-余弦-直线运动规律中3段的凸轮转角比例,可使从动件的运动位移发生改变,满足不同多梳栉经编机机型对槽针运动轨迹形状的要求。
非对称直线-余弦-直线运动规律不仅加速度曲线连续、光滑,跃度曲线也连续,保证运动过程无冲击,利于提高整机转速。与算例中选定的一种非对称余弦加速度运动规律相比,非对称直线-余弦-直线运动规律的加速度和跃度极值都有不同程度的下降,对提升机器的转速有利。对于经编机槽针运动,由于其运动的特点必须在非对称运动规律前提下,而非对称直线-余弦-直线运动规律具有加速度曲线连续、光滑,跃度曲线连续的优点,应是较好的方案。
实际经编机产品运转效果表明,采用非对称直线-余弦-直线运动规律不仅很好地满足了经编机编织工艺要求,也提高了整机的运转速度。
[1] 曹清林,王小霞,黄骏.多梳经编机复合针运动机构的设计[J].江苏技术师范学院学报,2011,17(4):1-9.CAO Qinglin,WANG Xiaoxia,HUANG Jun.Design on the compound needle mechanism of the warp knitting machines[J].Journal of Jiangsu Teachers University of Technology,2011,17(4):1 -9.
[2] 曹清林,黄骏,刘莉萍,等.多梳栉经编机成圈机件的运动研究[J].纺织学报,2014,35(11):155 -160.CAO Qinglin,HUANG Jun,LIU Liping,et al.Study on kinematic of loop-forming elements in warp knitting machine with multi-guide bars[J].Journal of Textile Research,2014,35(11):155 -160.
[3] 沈世德.实用机构学[M].北京:中国纺织出版社,1997:158-160.SHEN Shide.Practical Mechanisms[M].Beijing:China Textile& Apparel Press,1997:158-160.
[4] 夏风林,葛明桥,蒋高明.高速经编机梳栉横移运动的优化设计[J].纺织学报,2009,30(5):118 -125.XIA Fenglin, GE Mingqiao, JIANG Gaoming.Optimizing design of shogging motion of the guide bar on high speed warp knitting machine[J].Journal of Textile Research,2009,30(5):118 -125.
[5] 王允地,王稳地,王良文.高级导数连续的凸轮从动件运动规律研究[J].陕西科技大学学报,2011,29(5):87-92.WANGYundi,WANG Wendi,WANG Liangwen.Research about continuous higher derivative motion rule of cam follower[J].Shaanxi University of Science and Technology,2011,29(5):87 -92.
[6] 刘昌祺,牧野洋,曹西京.凸轮机构设计[M].北京:机械工业出版社,2005:39-41.LIU Changqi,MOUYE Yang,CAO Xijing.Design of Cam Mechanism[M].Beijing:China Textile& Apparel Press,2005:39 -441.
[7] 陈继生,张彩丽.自动机械的凸轮机构运动规律及其通用性研究[J].机械设计与制造,2008(3):221-222.CHEN Jisheng,ZHANG Caili.Research on the low of motion and universality about the cam mechanism of automation[J].Machinery Design and Manufacture,2008(3):221-222.
[8] 杨书林,罗建东,龚德祥.从动件运动规律的通用表达式及在凸轮设计中的应用[J].机械科学与技术,2002,21(6):913 -914.YANG Shulin,LUO Jiandong,GONG Dexiang.The general formula of the motion specifications of a cam mechanism follwer and its application to the cam optimal design[J].Mechanical Science and Technology,2002,21(6):913-914.
[9] 沈世德.高低速凸轮机构运动方程[J].机械工程学报,1992,28(4):78 -85.SHEN Shide.The universal kinematic equation of high or low speed cam mechanism[J].Chinese Journal of Mechanical Engineering,1992,28(4):78 -85.
[10] 王丞,孙益峰,张骏.凸轮从动件运动规律完整通用表达式设计及软件应用[J].机械传动,2008,32(6):68-71.WANG Cheng,SUN Yifeng,ZHANG Jun.Design of the general formula of the motion specifications of cam mechanism follwer and its software appliance [J].Journal of Mechanical Transmission,2008,32(6):68 -71.
