一种稳健的混合范数约束的波束综合算法*

尚欢欢，周 林，赵华侨，高火涛，刘克刚

(武汉大学 电子信息学院，武汉 430072)

1 引言

在雷达和通信系统设计中，为抑制干扰和噪声，往往要求天线的方向图具有特殊的形状［1］。至今，已出现了大量的波束综合算法，如经典的Dolph－Chebyshev 方法［2］、泰勒(Taylor)方法等［3］，但是，这些方法对阵列形式有严格的要求。Olen 和Compton［4］基于自适应理论提出了比较系统的迭代方法;Zhou 等［5］以阵列效率为约束条件，提出了指定旁瓣下的超方向性波束形成算法，但是，自适应阵列综合算法普遍存在迭代收敛的问题。

近年来，研究人员提出了大量的基于凸优化理论的波束综合算法。鄢社峰等［6］提出了可以同时兼顾波束形成中多个性能指标的波束综合算法，甘甜等［7］提出了一种稳健的恒定束宽的波束形成算法，运用凸优化理论将波束综合问题转化为凸优化形式的约束问题，通过工具箱CVX 或SeDuMi 求得问题的最优解。信号的稀疏表示是一种新的分析方法，已在诸多领域体现出其优势。Zhang 等［8］通过在波束综合的约束条件中添加稀疏表示准则，有效地降低了波束的旁瓣水平;刘翼鹏等［9］提出了一种混合范数约束的波束综合算法。然而，文献［8－9］仅对波束的旁瓣进行控制而未对算法的稳健性和阵列效率等性能参数进行详细分析。

基于此，本文提出了一种基于敏感度和混合范数约束的波束综合算法。仿真实验表明，只要合适地选取敏感度因子和其他参数的取值，便能得到有较低旁瓣和零陷的波束响应图。通过分析可知，该算法具有良好的稳健性，能容忍较大的幅相误差，而且阵列的效率也有较大的提高。

2 波束形成及相关参数定义

现假设有一均匀圆阵，由M个各向同性的阵元组成，阵列的半径为r，如图1 所示。

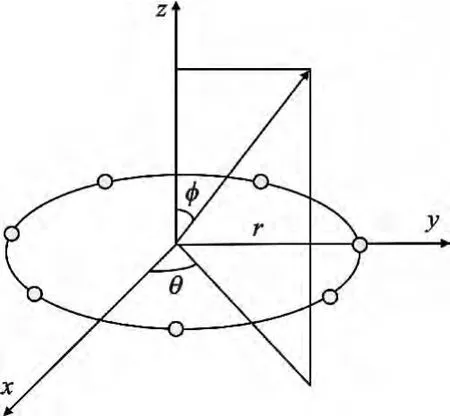
图1 均匀圆阵Fig.1 Uniform circular array

现有一波长为λ 的远场窄带平面波从(θm，φm)方向入射到天线阵中，其导向矢量a(θ，φ)可以表示为

式中，τi=rsin(θ)cos (iβ－)，i=0，1，2，…，M－1，β=2π/M，在这里φ 指信源的俯仰角，θ 指信源的方位角。w 表示阵列的加权系数，则波束形成器的输出响应可表示为

可以直接得到常规波束形成(Conventional Beamforming，CBF)的权值为Wcbf=a(θm，m)。一般把最大方向性增益定义为阵列的方向性系数，可以表示为

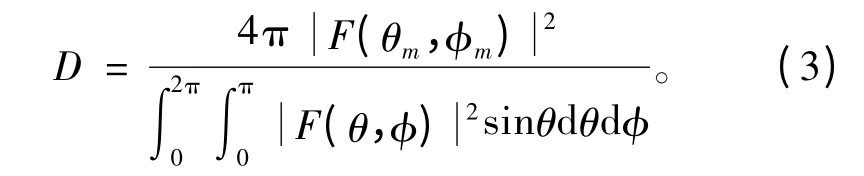
由式(2)和式(3)可知，方向性系数D 可以进一步表示为两个二次型比值:

式中，矩阵N、R 为两个确定的矩阵，分别表示为

假设本文所用的天线阵由短偶极子天线构成，则矩阵R 可以表示为

式中，dij是指两个阵元之间的距离，Rij是指矩阵R的第i 行第j 列元素。

在波束形成过程中，为控制主瓣的形状和降低旁瓣电平，通常都会对各阵元施加不等的加权值。然而，对阵元的不均匀加权容易导致阵列效率的损失，阵列效率η［10］可以表示为

为更好地表征阵列天线对阵列误差的敏感性，本文引入阵列敏感度因子［11］K，一般K 值越小波束稳定性越好，反之越容易受误差影响。

3 最小均方准则法(MMSE)

在波束形成过程中，一般都期望接收的功率尽量集中在主瓣，而副瓣接收的越少越好。反映在方向图上，就是主瓣越窄越好，副瓣电平越低越好。为方便起见，以下的俯仰角均为90°，方位角以θ 表示，则有

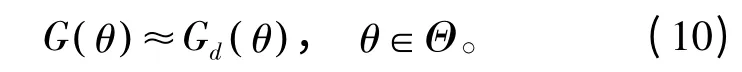
式中，G(θ)=wHa(θ) 与Gd(θ) 分别表示θ 方向的设计波束响应和期望波束响应，Θ 表示波束形成的观察区域。一般设计的波束响应不会与期望的波束响应完全一致。于是，一般都要求设计波束响应和期望波束响应之间的误差越小越好。这个误差的大小可以用加权误差范数来衡量，加权误差范数越小说明设计的波束响应越接近期望波束响应，即

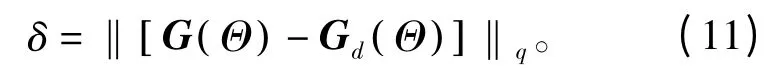
最小均方准则法(Minimize Mean Square Error，MMSE)即当q=2 时误差范数δ 达到最小的情况，可以表示为w

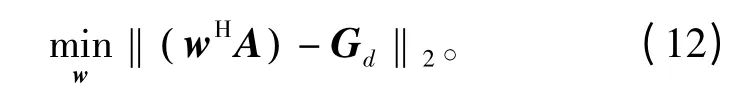
式中，A 为一个M × L 维的矩阵，表示方向角在[0°，360°)范围内，采样间隔为Δθ 的阵列流型矩阵，A=[a (θ1)，…，a (θi)，…，a (θL)]，θj∈Θ，L=360°/Δθ+1。

式(12)不需要凸优化工具包就可以进行求解，直接用Lagrange 乘子法得到最优解为

4 稀疏表示的混合范数法

低旁瓣、零陷和稳健性是波束综合的重要性能参数。现假设有P个干扰源，指定零陷的深度为U1，则零陷的响应值满足ε1=，零陷约束值可以写为

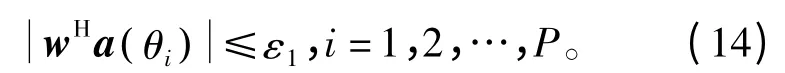
波束的旁瓣和零陷容易受阵列误差的影响而发生畸变，因此在波束设计过程中既要考虑旁瓣和零陷水平也要考虑其稳健性。敏感度因子K 反映了阵元间的不稳定性，因此可以在波束综合中对K 进行约束，从而提高算法的稳健性。

理想波束的阵列增益满足稀疏分布中大部分元素为0(或接近0)而少部分元素为1(或接近1)的特性，基于此，可以考虑在阵列增益的基础上添加稀疏约束。阵列增益具有次级结构特征，即阵列增益向量中较大元素集中在主瓣区域，而较小元素分布在旁瓣区域;又由于l1范数最小化约束可以激励稀疏约束，而l! 范数最小化约束可激励密集分布的约束。因此，分别对波束的主瓣和旁瓣使用l! 范数约束和l1范数约束。则加入稀疏表示后的波束综合模型为

式中，δ 为设计波束响应与期望波束响应之间的误差;AM表示主瓣区域对应的阵列流型矩阵，为一个M×Q 矩阵，Q 为主瓣区域离散化后的长度;AS表示旁瓣区域对应的阵列流型矩阵，为一个M×(L－Q)矩阵，L 为整个观测区域离散化后的长度;目标函数中向量乘积wHAM表示波束图主瓣内的阵列增益;而wHAS表示波束图旁瓣部分的阵列增益，|wHa(θi)|≤ε1表示对某个干扰方向的约束;K 为敏感度因子。该问题是一个凸优化问题，可以用凸优化工具CVX 进行求解。

5 仿真实验与分析

5.1 仿真实验1:无阵列误差情况下算法性能

实验条件:假设有一均匀圆阵，工作频率为f=10 MHz，阵列半径为r=0.15λ，阵列由M=7 根短偶极子天线组成。主波束对准方向为θs=180°，干扰源方向θi=30°，零陷深度ε1=－50 dB，敏感度因子K=0.5。期望波束响应:在θs=180°方向的波束响应为1，在旁瓣区域 ΩSLL=[0°，θs－θp)∪[θs+θp，360°)的期望响应为0，其中θp=15°，取Θ=θs∪ΩSLL，并对该区域进行离散化处理。图2 所示为期望波束的响应图。

图2 期望波束响应Fig.2 Desired beam pattern

图3 所示为常规波束形成、最小均方准则法和混合范数约束法三种算法的波束响应图。由图3 可知CBF 的主瓣宽度很宽，方向性较差;最小均方准则法的旁瓣电平较高，而本文算法的旁瓣电平较低均在－28 dB 以下，并且在干扰方向形成较深的零陷。

图3 三种算法的波束响应Fig.3 Beam patterns about the three methods

由表1 可知，MMSE 的最高旁瓣为－14.4 dB，而本文算法的最高旁瓣为－28.3 dB。本文算法的阵列效率η 与MMSE 相比较也有较大提高。此外，本文算法的敏感度因子K 比MMSE 要小很多，由此，可以大致认为本文算法比MMSE 有更好的稳健性。下面针对算法的稳健性作详细分析。

表1 三种算法的各性能参数比较Table 1 Performance of three algorithms

5.2 仿真实验2:存在阵列误差情况下算法性能

对于阵列误差，本文主要考虑通道的幅度误差和相位误差，假设幅相误差均满足独立的高斯分布。算法的最大可容忍误差可以反映波束形成器的稳健性，其值是通过蒙特卡洛实验估计得到［12］。在每一个给定的随机幅相误差的情况下，进行多次重复实验，如果波束图的畸变程度还在可接受范围以内，那么可以认为对于这种程度的幅相误差波束形成的波束图是稳健的;随着阵列幅相误差的不断增大，当波束图的畸变变得不可接受，那么在此之前的一个幅相误差值作为最大可容忍的阵列幅相误差。

(1)假设只存在幅度误差时，为表示简单这里用δ1 表示。以3 dB为步长，从－37 dB到－28 dB观察波束图的变化情况，如图4 所示。

图4 不同幅度误差下本文算法波束图变化情况Fig.4 Radiation patterns for the proposed method when sensors exist amplitude errors

(2)假设只存在相位误差时，为表示简单这里用δ2 表示。以0.5°为步长，从1°到2.5°观察波束图的变化情况，如图5 所示。

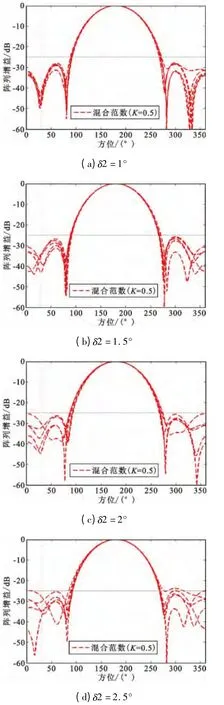
图5 不同相位误差下本文算法波束图变化情况Fig.5 Radiation patterns for the proposed method when sensors exist phase errors

从图4(a)～(d)的变化情况可知，随着幅度误差的变化，波束的形状也随着变化。当幅度误差为－28 dB时，波束的旁瓣发生明显畸变，零点位置和增益也发生较大变化，所以在这里可以认为算法所能容忍的最大幅度误差约为－30 dB。从图5(a)～(d)可以看出，随着相位误差的增大，波束响应图也随着变化。当阵列的相位误差达到2.5°时，波束的旁瓣和零点位置发生明显畸变，此时，可以认为算法所能容忍的最大相位误差约为2°。

为比较最小均方准则法和本文算法的稳健性，现假设阵列的幅相误差分别为δ1=－30 dB，δ2=1.5°，其他实验条件同仿真实验1，观察这两种算法在存在幅相误差情况下的稳健性能，如图6 所示。

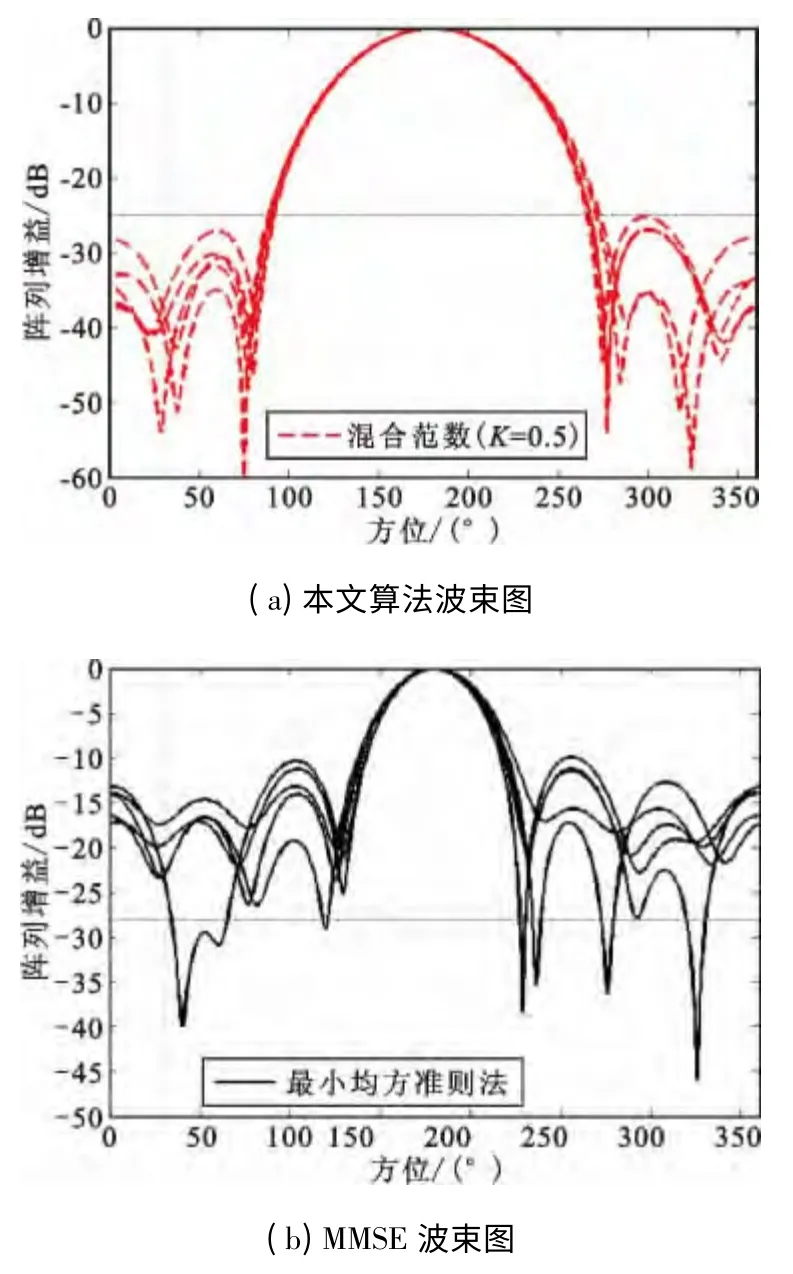
图6 存在幅相误差时MMSE 算法和本文算法的稳健性Fig.6 The robustness performance of the MMSE method and the proposed method

从图6(a)和(b)的对比可知，当存在相同阵列幅相误差时，本文算法波束形状保持较好，而最小均方准则算法的波束旁瓣发生明显的畸变。因此，可以得出本文算法相比最小均方准则下的波束形成算法具有更好的稳健性。

6 结束语

结合凸优化理论和信号的稀疏表示准则，本文提出了一种新的混合范数约束下的波束综合算法。在阵列增益的基础上添加稀疏约束，可以促使波束图向理想波束响应成形。仿真实验证明，新方法的波束响应具有更低的旁瓣和零陷，其最高旁瓣和最低零陷深度分别为－28 dB和－50 dB左右，因此，能够有效降低噪声和干扰对信号的影响。多次实验表明，与MMSE 算法相比，本文提出的算法具有良好的稳健性，因此可以保证波束图在阵列存在残留误差的情况下不发生严重畸变;算法运用凸优化工具包CVX 进行求解，计算方便、简单。

［1］Wang Z X，He Z S，Hu J F，et al.A low side－lobe array weighted optimization method in sky－wave radar［C］//Proceedings of 2013 IEEE International Symposium on Phased Array Systems ＆ Technology.Waltham，MA:IEEE，2013:379－382.

［2］Dolph C L.A current distribution for broad－side arrays which optimizes the relationship between beamwidth and side－ lobe level［J］.Proceedings of the IRE，1946，34(6):335－348.

［3］Taylor T.Design of circular apertures for narrow beamwidth and low sidelobes［J］.IRE Transactions on Antennas and Propagation，1960，8(1):17－22.

［4］Olen C A，Compton J R T.A numerical pattern synthesis algorithm for arrays［J］.IEEE Transaction on Antennas and Propagation，1990，38(10):1666－1676.

［5］Zhou Q C，Gao H T，Zhang H J，et al.Pattern synthesis method applied in designing HF super－directive receive arrays［J］.IEICE Electronics Express，2013，10(21):1－7.

［6］鄢社峰，马远良，孙超.任意几何形状和阵元指向性的传感器阵列优化波束形成方法［J］.声学学报，2005，30(3):264－270.YAN Shefeng，MA Yuanliang，SUN Chao.Beam－pattern optimization for sensor arrays of arbitrary geometry and element directivity［J］.Acta Acustica，2005，30(3):264－270.(in Chinese)

［7］甘甜，王英民.一种稳健的恒定束宽的波束形成算法［J］.声学学报，2012，37(1):18－24.GAN Tian，WANG Yingmin.A robust broad band beamforming method of constant beam width［J］.Acta Acustica，2012，37(1):18－24.(in Chinese)

［8］Zhang Y，Ng B P，Wan Q.Sidelobe suppression for adaptive beamforming with sparse constraint on beam pattern［J］.Electronics Letters，2008，44(10):615－616.

［9］Liu Y P，Wan Q.Sidelobe suppression for robust beamformer via the mixed norm constraint［J］.Wireless Personal Communications，2012，65(4):825－832.

［10］刘晓莉，廖桂生，曾操.最大化阵列效率的方向图综合方法［J］.西安电子科技大学学报，2009，36(5):807－812.LIU Xiaoli，LIAO Guisheng，ZENG Cao.Pattern synthesis method for array efficiency maximization［J］.Journal of Xidian University，2009，36(5):807－812.(in Chinese)

［11］Zhou Q C，Gao H T，Zhang H J，et al.Superdirective Beamforming with Interferences and Noise Suppre－ssion via Second－ Order Cone Programming［J］.Progress in Electromagnetics Research C，2013，43:255－269.

［12］Zhou Q C，Gao H T，Zhang H J，et al.Robust Superdirective Beamforming for HF Circular Receive Antenna Arrays［J］.Progress in Electromagnetics Research，2013，136:665－679.