小孔径超视距目标探测中的OFD－NLFM 发射波形设计*

贺 青，罗来源，姚山峰

(盲信号处理重点实验室，成都 610041)

1 引言

天波超视距雷达(Over－ the－ Horizon Radar，OTHR)是远距离目标探测的有效手段，它工作在短波频段，利用电离层反射实现1000～4000 km 的目标探测［1］。但是，OTHR 接收阵列一般达到了千米级［2］，开销较大，部署受限。为此，提出一种基于小孔径接收圆阵的超视距目标探测系统，圆阵直径为400 m，用于解决传统天波超视距雷达部署受限的问题。阵列孔径的减小将导致系统的空域滤波性能下降，即噪声和杂波抑制能力恶化，探测距离降低［3］。本文从波形设计角度出发，研究弥补系统性能损失的方法。近年来针对天波超视距雷达新型波形设计主要以文献［4－6］的研究成果为代表，提出了时间间隔线性调频连续波信号［4］和正交频分复用线性调频信号［5－6］，用以解决强大海杂波背景下的舰船目标检测问题以及抑制扩展多普勒杂波。但是针对小孔径超视距目标探测时提升系统性能的波形设计方法研究较少，相似的研究主要集中在多输入多输出(Multiple－Input Multiple－Output，MIMO)雷达波形设计中，为了获得更好的脉压主瓣和旁瓣性能，学者们提出了正交频分复用线性调频信号［7］，这种信号利用了子带信号间的正交性可以获得较窄的脉压主瓣宽度，但是旁瓣电平较高。为了进一步抑制旁瓣水平，文献［8］提出了低旁瓣脉压优化方法，文献［9］提出了抑制特定区域的恒模波形优化方法，文献［10］提出了适应通道误差稳健波形优化方法。考虑到正交频分复用信号在进行脉压优化设计时为了获取更低的旁瓣电平，采用加权处理会牺牲一定的脉压处理信噪比。为此有学者提出了采用非线性调频信号来解决这个问题，并将其应用到MIMO 体制中设计了正交频分非线性调频信号［11］。它利用相位逗留原理［12］进行设计，避免了加权带来的信噪比损失问题。目前，针对非线性调频(Nonlinear Frequency Modulation，NLFM)信号的设计往往都是采用窗函数求反并积分的方法，由于其依据的相位逗留原理实际上是一个函数的近似解，这都使得产生的NLFM 信号性能恶化，而且对信号参数较为敏感。

针对上述问题，本文第2 部分分析了孔径减小后阵列波束形成与传统天波超视距雷达阵列波束形成的差别，在此基础上给出波形设计的准则;第3 部分对正交频分非线性调频(Orthogonal Frequency Division－ Nonlinear Frequency Modulation，OFD－NLFM)发射信号进行建模并分析了其参数设置方法;第4 部分提出了基于凸优化的旁瓣抑制方法，推导了算法原理和实现步骤;最后，通过仿真验证了信号和算法的性能。

2 波形设计准则

根据阵列天线原理，天线增益和阵列方向图是影响系统性能的关键参数，当采用小孔径圆阵作为接收阵列时，由于阵列尺寸和阵元数的下降必然带来性能的损失，下面以一个仿真进行说明。假设天波超视距雷达传统接收阵列为均匀线阵，阵列长度2.5 km，阵元数400;小孔径接收阵列为均匀圆阵，直径为380 m，阵元数80;工作频率为6 MHz，来波仰角10°，两个阵列都采用常规波束形成，其方向图如图1 所示。

图1 均匀线阵和均匀圆阵波束形成图Fig.1 The beamforming of the traditional linear array and the small aperture circular array

从图中可以看出，采用小孔径圆阵时阵列增益下降约8 dB，主瓣展宽约5 倍，旁瓣电平大幅升高。因此，采用圆阵后阵列的分辨率、噪声/干扰的空域抑制能力、信噪比等信号接收性能将大幅下降，小孔径系统将会面临更加恶劣信号接收质量。为此，本文从波形设计的角度出发，设计一种新型波形，要求该波形可以适应更低的噪声和干扰环境，弥补阵列孔径减小带来的损失。为此得出波形设计准则如下:

(1)设计波形带宽尽可能大，提升目标距离分辨率，改善接收信杂比;

(2)设计波形的脉压主瓣尽量窄，降低同一距离门内噪声、干扰和杂波的影响;

(3)设计波形的脉压旁瓣尽量低，降低目标距离门外噪声、干扰和杂波的影响;

(4)波形带宽增加不能增加选频段的难度，在提升距离分辨率的同时，还要考虑频带如何选择的问题。

3 基于正切函数的OFD－NLFM 信号建模

正交频分非线性调频雷达信号采用多个阵元天线发射相互正交的信号，在接收端通过匹配滤波完成信号处理。假设发射天线阵元数为M，T 为脉冲宽度，B 为每一个阵元信号带宽，Fc为信号载频，fz为每个阵元信号间的频率间隔。与OFD－LFM 信号类似，为了满足子带信号间的正交性，需要保证fz≥B［13］，则第i个阵元的发射信号为

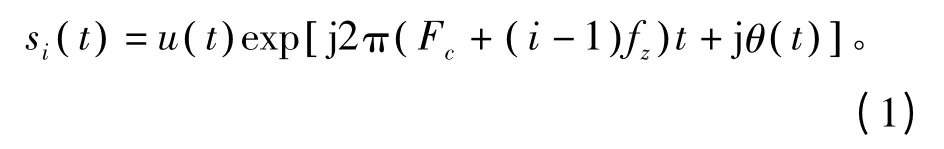
式中，θ(t) 即为待求的相位函数。

下面求解相位函数θ(t)，这里以正切函数作为非线性调频信号的频率函数:

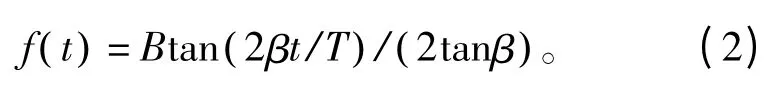
式中，β=arctanα，α 为时间副瓣电平控制因子［14］。

根据信号瞬时频率和相位的关系，可以得到相位函数为

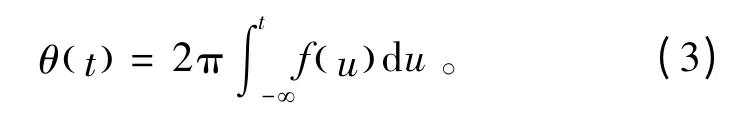
上式中的积分可以通过数字积分法进行求解。将式(2)和式(3)代入式(1)即可求得OFD－NLFM信号。在求得信号后，发射端采用多元天线进行信号发射，接收端每一个阵元对不同子带信号分别进行脉压处理，随后联合所有接收阵元的信号进行波束形成处理即完成多输入多输出体制的信号处理流程。文献［13］证明了对所有阵元信号进行相位补偿后采用相参合成可以使得带宽变为单个阵元信号带宽的M 倍，相应的距离分辨率提升M 倍，所以将MIMO 体制的思想用于小孔径超视距目标探测一方面降低了短波频段频带的选择难度，另外一方面也提升了系统的距离分辨率。

采用正切函数作为频率函数求解非线性调频信号避免了对群时延函数求反的运算，相比基于窗函数的方法更为简单，而且避免了相位逗留法求解时近似带来的脉压波形不理想的问题。但是时间副瓣电平控制因子的选择对脉压结果有所影响，文献［14］指出α 不能任意大，否则脉压波形将会失真。下面给出α 的选择依据。前面第一节已经给出了波形设计的准则，主要是希望脉压主瓣尽量窄，旁瓣尽量低，因此主要考察α 对脉压主瓣和旁瓣的影响。假设α∈[0 10]，图2 给出了主瓣宽度和峰值旁瓣随α 的变化情况。

图2 脉压主瓣宽度和峰值旁瓣随α 变化图Fig.2 Mainlobe width and peak side－lobe of the pulse compression at different α

从图中可以看出，脉压主瓣和峰值旁瓣随α 的变化趋势正好相反，即要获得窄的主瓣和低的旁瓣是一对矛盾，因此在选择α 的时候需要结合实际情况进行折衷选择，在本文中考虑到短波进行目标探测时距离门一般在20 km 左右，考虑后续峰值旁瓣可以通过优化算法进一步降低，为此选择主瓣尽量窄，即α=1。

4 基于凸优化的脉压旁瓣抑制算法

OFD－NLFM 信号采用相参合成以及选择合适的α 后距离分辨率提升，主瓣变窄，但是旁瓣依旧较高，为此本文提出一种基于凸优化的脉压旁瓣优化方法。首先将脉压合成后的结果写成向量形式:

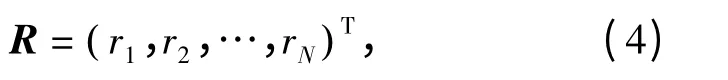
然后建立优化模型，寻找一组与R 长度相等的权值w=(w1，w2，…，wN)T，使得优化后的主瓣尽量窄，旁瓣尽量低。为了表征这个结果，设定目标函数为脉压输出的噪声功率最小［15］，即

式中，‖·‖表示取向量的模即向量2 范数。下面求解条件函数，其中第一个条件函数考虑主瓣范围内的脉压输出是恒定的，不失一般性地可以表示为1;第二个条件函数考虑峰值旁瓣电平小于一个期望的设定值，假设为ε。为了表示上述两个条件函数将R 构造成如下矩阵:

假设脉压输出结果主瓣区域有k个点，则保留L 矩阵中中间一列和左右各k/2 列，从而构造A 矩阵表示脉压主瓣区域:

则第一个限制条件为

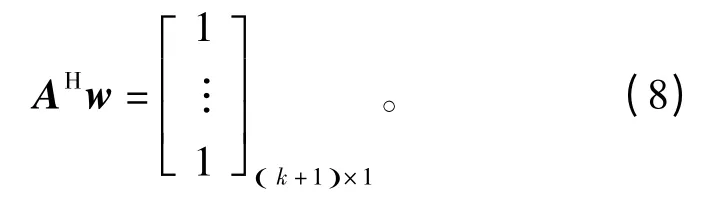
由L 矩阵去掉N 列以及其左右各k/2 列，得到矩阵B，表示脉压旁瓣区域:

则第二个限定条件为

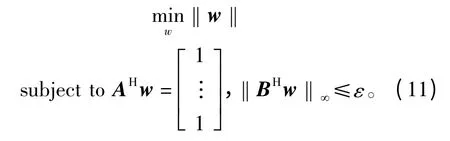
式(11)为一凸优化问题，可以利用凸优化工具进行求解，得到优化的权值向量w，即可求出最终的脉压优化结果

5 算法实现及仿真

本节针对前文提出的算法进行仿真，主要分析OFD－NLFM 信号的正交性、优化后的脉压性能和对噪声/干扰的抑制能力。

5.1 仿真1:设计的OFD－NLFM 信号正交性

仿真参数设定为发射阵元3个，信号脉宽10 ms，每个阵元信号带宽10 kHz，正交频率偏移集为［0 kHz 10 kHz 20 kHz］，α=1，信号采样率为25 kHz，信号载频为6 MHz，信号处理均为变为基带后的处理，假设电离层稳定且只有单模式传播，得到结果如图3 和图4 所示。

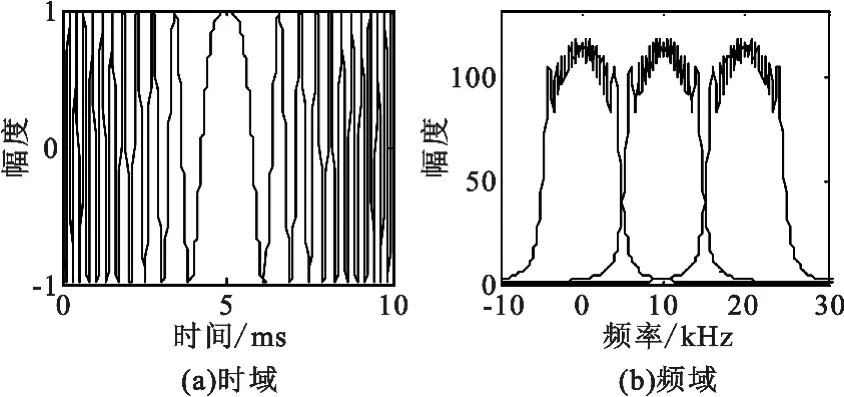
图3 OFD－NLFM 信号时域和频域图Fig.3 Time－domain and frequency－domain figure of the OFD－NLFM

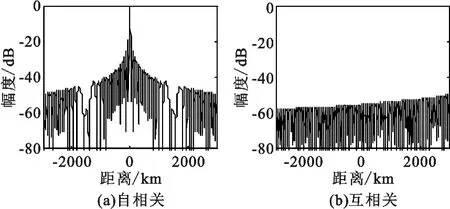
图4 OFD－NLFM 子带信号自相关和互相关图Fig.4 The auto－correlation and cross－correlation of the OFD－NLFM signal

图4(a)为子带信号1 的自相关，(b)为子带信号1 和子带信号3 的互相关(其余各子带互相关结果相同)，从图中可以看出互相关最大峰值低于50 dB，可见设计的OFD－ NLFM 信号的正交性能良好。

5.2 仿真2:优化后的OFD－NLFM 脉压性能

仿真参数设定与仿真1 相同。分别对LFM、OFD－NLFM 和优化后的OFD－NLFM 信号进行脉压仿真，其中凸优化中峰值旁瓣期望低于－30 dB，采用频域脉压技术，得到结果如图5 所示。

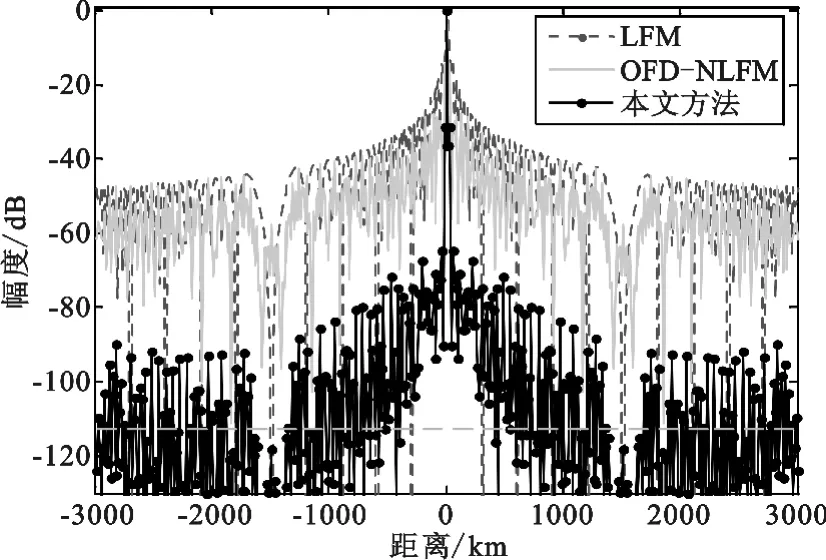
图5 三种信号脉压结果比较Fig.5 The pulse compression result of three signals

从图5 中可以看出，采用OFD－NLFM 信号主瓣宽度下降，大约为单个LFM 信号的1/3。优化加权以后主瓣略小于OFD－NLFM 的主瓣宽度，旁瓣明显下降，其中本文提出方法的峰值旁瓣为－31.22 dB，明显低于其他两种信号。图中的灰色黑线代表提出方法的脉压旁瓣均值(低于－100 dB)，远小于另外两种信号的旁瓣均值。

5.3 仿真3:优化后的OFD－NLFM 抗噪声性能

假设回波信号的信噪比均为－30 dB，其余仿真参数与仿真1 相同，得到结果如图6 所示。

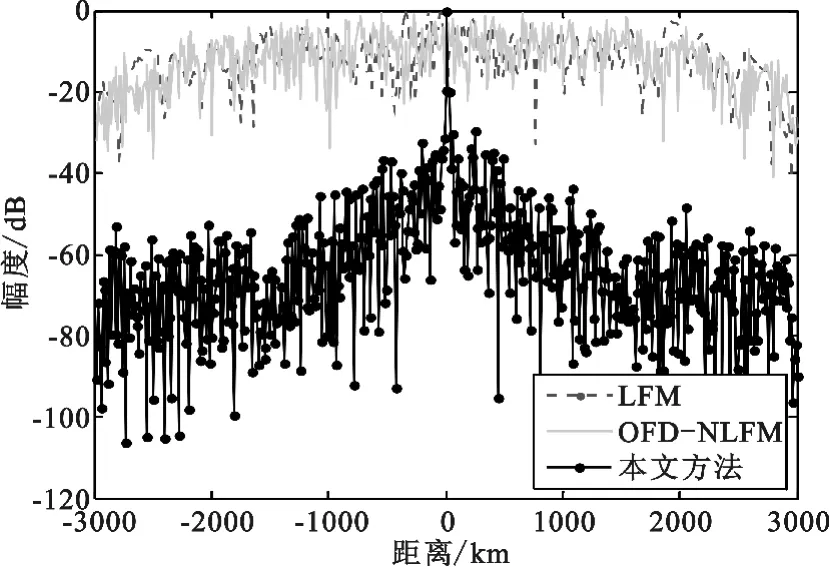
图6 信噪比－30 dB 时三种信号脉压结果比较Fig.6 The pulse compression result of three signals when SNR=－30 dB

从图6 中可以看出，当接收信号信噪比为－30 dB时LFM 信号和OFD－NLFM 信号都无法通过脉压进行有效的目标检测，而本文提出的算法仍然超过获得了20 dB左右的脉压输出信噪比。

5.4 仿真4:优化后的OFD－NLFM 抗干扰能力

假设真实目标距离雷达接收站450 km，干扰目标距离雷达接收站900 km，干扰信号回波功率高于目标30 dB，其余仿真参数与仿真1 相同，得到脉压结果如图7 所示。

图7 干扰存在时三种信号脉压结果比较Fig.7 The pulse compression result of three signals in interference environment

图7 说明当干扰存在时LFM 信号和OFD－NLFM 信号在干扰处(900 km)的脉压幅度均高于真实目标处(450 km)的脉压幅度值，目标检测将会失效，而本文提出的方法仍然有效。

通过上面分析来看，这种基于凸优化的OFDMLFM 信号设计方法不仅具有较高的距离分辨率，同时峰值旁瓣低，可以很好地抑制噪声和干扰的影响。

6 结束语

本文采用正切函数作为频率函数构建OFD－NLFM 信号并提出了一种基于凸优化的旁瓣抑制算法用于改善小孔径面临的性能差异问题，理论推导和仿真表明采用的方法可以从信号设计和脉压角度改善由于阵列孔径减小而带来的空域滤波性能恶化问题，方法比常规天波雷达采用的LFM 信号具有更窄的主瓣和更低的旁瓣性能，抗噪声和抗干扰能力更强。本文设计的信号和脉压处理方法为小孔径超视距目标探测提供了一种可行的信号设计方案，为其走向工程化奠定了基础。下一步可以从波束形成的角度进行研究，探讨用于改善小孔径空域滤波性能的波束形成新方法。

［1］Tang X D，Han Y J，Zhou W Y.Skywave Over－the－Horizon Backscatter radar［C］//Proceedings of 2001 CIE International Conference on Radar.Beijing:IEEE，2001:90－94.

［2］Thomason J F.Development of Over－the－Horizon Radar in the United States［C］//Proceedings of 2003 IEEE International Radar Conference.Huntsville，Alabama:IEEE，2003:599－601.

［3］He Q，Luo L Y.Analysis of Over－the－Horizon Target Detection Based on the Small Aperture Array［C］//Proceedings of 2014 7th International Congress on Image and Signal Processing.Dalian:IEEE，2014:1247－1251.

［4］Frazer G J.Mode－ selective OTH Radar:Experimental Results for One－ way Transmission via the Ionosphere［C］//Proceedings of 2011 IEEE Radar Conference.Kansas City，MO:IEEE，2011:397－402.

［5］Frazer G J，Abramovich Y I，Johnson B A.Multiple－Input Multiple－Output Over－the－Horizon Radar Experimental Results［J］.IET Radar Sonar Navigation，2009，3(4):290－303.

［6］Abramovich Y I，Frazer G J，Johnson B A.Principles of Mode－Selective MIMO OTHR［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49(3):1839－1868.

［7］刘波，韩春林，苗江宏.MIMO 雷达正交频分LFM 信号设计及性能分析［J］.电子科技大学学报，2009，38(1):28－31.LIU Bo，HAN Chunlin，MIAO Jianghong.OFD－ LFM Signal Design and Performance Analysis for MIMO Radar［J］.Journal of University of Electronic Science and Technology of China，2009，38(1):28－31.(in Chinese)

［8］何学辉.基于凸优化的雷达波形设计及阵列方向图综合算法研究［D］.西安:西安电子科技大学，2010.HE Xuehui.Study on Radar Waveform Design and Array Pattern Synthesis Based on Convex Optimization［D］.Xi'an:Xidian University，2010.(in Chinese)

［9］李风从，赵宜楠，乔晓林.抑制特定区间距离旁瓣的恒模波形设计方法［J］.电子与信息学报，2013，35(3):532－536.LI Fengcong，ZHAO Yinan，QIAO Xiaolin.Constant Modular Waveform Design Method for Suppressing Range Sidelobes in Specified Intervals［J］.Journal of Electronics ＆ Information Technology，2014，42(11):2331－2336.(in Chinese)

［10］张向阳，廖桂生，许京伟，等.非完备目标先验知识多输入多输出雷达稳健波形设计［J］.电波科学学报，2014，29(6):1036－1044.ZHANG Xiangyang，LIAO Guisheng，XU Jingwei，et al.Robust Waveform Design for MIMO Radar With Imperfect Target Prior Knowledge［J］.Chinese Journal of Radio Science，2014，29(6):1036－1044.(in Chinese)

［11］赵伟，赵永波，李慧，等.MIMO 雷达正交频分非线性调频波形设计［J］.电子学报，2014，42(11):2331－2336.ZHAO Wei，ZHAO Yongbo，LI Hui，et al.Orthogonal Frequency Division－ Nonlinear Frequency Modulation Waveform Design for MIMO Radar［J］.Acta Electronica Sinica，2014，42(11):2331－2336.

［12］Vizitiu I，Anton L，Popescu F，et al.The Synthesis of Some NLFM Laws Using the Stationary Phase Principle［C］//Proceedings of 10th International Symposium on Electronics and Telecommunications.Timisoara:IEEE，2012:377－380.(in Chinese)

［13］彭尚，王党卫，贺照辉，等.OFDM－MIMO 相控阵雷达带宽合成方法研究［J］.空军预警学院学报，2015，29(1):1－6.PENG Shang，WANG Dangwei，HE Zhaohui，et al.Method of Bandwidth Synthesis of OFDM－ MIMO Phased Array Radar［J］.Journal of Air Force Early Warning Acdemy，2015，29(1):1－6.(in Chinese)

［14］Skolnik M I.Radar handbook［M］.3rd ed.New York:McGraw－Hill Publishing House，2010.

［15］刘聪锋.稳健自适应波束形成算法［M］.西安:西安电子科技大学出版社，2012.LIU Congfeng.Robust Adaptive Beamforming Algorithms［M］.Xi'an:Xidian University Press，2012.(in Chinese)