一种盲签名电子现金系统方案的设计与实现
2015-12-25白永祥
白永祥
(1渭南职业技术学院陕西渭南714000;2西北大学信息与科技学院陕西西安710127)
0 引言
随着网络信息化技术的快速发展,电子支付在电子商务交易中成为核心的技术,电子现金以其关键的技术将会得到广泛的应用。为了能跟踪重复支付的用户,在电子现金流动的过程中加入了盲化的用户身份信息,在普通的盲签名中,被签名的消息整个由用户所控制,而签名者对此一无所知,这样很容易造成签名被犯罪分子利用。基于身份的公钥密码体制与传统的密码体制相比较在很多方面都具有更多的优势,通过基于身份的密码技术来构建部分盲签名方案[1],并基于部分群盲签名方案设计公平离线的电子现金系统。
1 相关概念
1.1 盲签名
1982年,Chaum在美国密码学会上提出了盲签名的概念[2]。它是用户和签名人之间的一个交互协议,签名人对用户的消息进行数字签名,但却不知道签名消息的具体内容,即便以后将签名公开,也无法追踪消息与自己执行签名过程之间的相互关系。
一个盲签名体制有签名人和用户,一般由满足如下条件的3个算法构成[3]:
1)初始化算法:形成系统参数与签名人的公钥、私钥,这是一个概率多项式时间算法。
2)盲签名生成算法:s=Sign(m,params,pk,sk),s代表签名,params代表公共系统参数,pk,sk代表签名者的公钥和私钥,Sign()是一个概率多项式时间的交互协议。
3)盲签名验证算法:1(0)←Verify(m,params,pk,s) ,1 表示签名有效,0表示签名无效。
1.2 电子现金
电子现金(Electronic Cash)又称为电子货币 (Electronic Money)或数字货币(Digital Cash),它是一种非常重要的电子支付系统,也可以被看作是现实货币的电子或数字模拟[4]。电子现金以数字信息形式存在,并通过计算机网络流通,但它比现实的货币更加方便和经济。一个电子现金系统最简单的形式包括商家、用户、银行三个主体和四个安全协议过程:初始化协议、提款协议、支付协议和存款协议。
电子现金系统在其生命周期中要经过取款、支付和存款三个过程[5],并涉及用户(Consumer)、商家(Merchant)和银行(Bank)三方。电子现金的基本流通模式有三种协议:一个是用户与银行执行取款协议,用户从注册银行提取电子现金ꎻ另一个是用户与商家执行支付协议支付电子现金ꎻ最后一种是商家与银行执行存款协议,将交易所得的电子现金存入商家的银行账户。电子现金的基本模型如图1所示[6]:
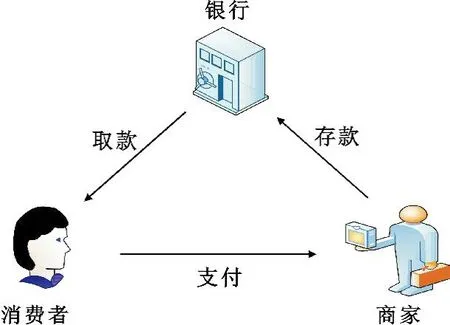
图1 电子现金基本模型
2 研究背景
电子现金支付旨在网络上重建基于现金型交易功能的作用,它可以使用密码技术和盲签名技术实现完全匿名,从而保护用户的消费信息。自从1982年Chaum最早提出一个在线的基于RSA盲签名完全匿名电子现金方案以来[7],研究者们提出了各种各样的方案。
1988年,Chaum、Fait、Naor利用切割-选择和 RSA 盲签名技术提出了一个在线的匿名电子现金方案[8]ꎻ1991年,Okamoto、ohta采用二叉树结构表示电子现金和利用切割选择技术的可分电子现金方案[9]ꎻ1992年,由Brands最早利用限制性盲签名提出了一个离线的完全匿名电子现金方案,这是迄今为效率最高的方案之一,1993 年又进行了改进[10]ꎻ1995 年,Stadler、Brickel分别提出公平电子现金方案,除具备一般电子现金的功能外,还可跟踪电子现金和所有者跟踪协议[11]。同年Birckel、Gemmel、Kravitz引入基于可信第三方 TTP的跟踪[12]。1996年,Frankel、Tsiounis、Yung基于间接证明技术提出了一个公平电子现金方案[13]ꎻ1997年,Davida、Frankel和Tsiounis基于零知识证明技术对上述方案进行了改进[14],1998年,Frankel、Tsiounis和 Yung在文献[15]利用同构加密的思想分两次对上面方案进行了改进ꎻ1998年,Anna、Zulfikar在文献[16]首先提出了基于群盲签构造一个具有多个银行参与发行的完全匿名电子现金方案ꎻ1999年,杨波等人在[17]中提出了选用灵通卡的公平电子现金方案。
3 方案设计
3.1 成员组成
方案由四部分组成:消费者、可信第三方(TTP)、银行、商家。为了整个系统的安全性,在公共网上传递信息采用公钥密码体制。盲签名方法用来保护用户信息的隐私,四部组成因素具体功能如下[18]:
1)消费者(Consumer):想用电子现金购买商品的消费者。
2)可信第三方(TTP):是一个各方都信认的认证机构,它可以为电子现金生成一些认证的信息,如果发生争执,可以正确识别身份。
3)银行(Bank):为消费者分配电子现金,并在消费者用电子现金购买商品后,可以为商家存款到账户。
4)商家(Merchant):能为消费者提供各种商品的可信赖方,并且能够检验出从消费者处获得的电子现金是否为银行分发的有效电子现金。同时能够把从消费者处获得的电子现金传送到银行,存储到自己的账户上。
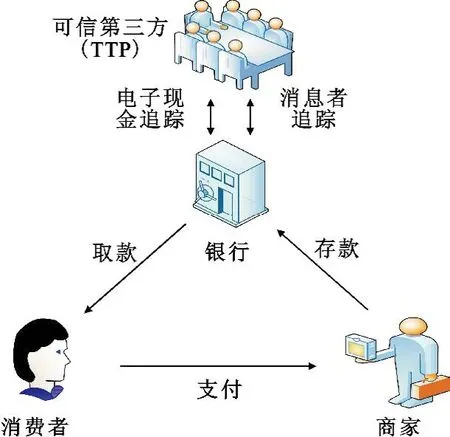
图2 一种公平离线的电子现金模型
3.2 方案中用到的符号
IDi:消费者i唯一的身份标识信息ꎻ
Ai:消费者i的银行账户ꎻ
Hash(.):单向杂凑函数ꎻ
sn:唯一的货币标识号ꎻ
PKi/SKi:用户i的公钥和私钥ꎻ
Ek(·)/Dk(·):加密/解密算法ꎻ
B(m,r):对消息进行盲因子的函数ꎻ
B-1(m,r):去盲因子函数。
3.3 协议过程
在我们的方案中,有四个协议过程:注册、取款、支付、存款。具体过程如下:
3.3.1 注册登记
1)客户为了得到银行对电子现金的权威认证,必须到银行进行注册登记,用户通过自己的私钥计算SC=ESKC(IDi)产生证明书,然后使用可信第三方的公钥加密后发送给TTP,EPKTTP(IDi,SC)ꎻ
2)TTP收到信息后,使用客户的公钥检验IDi=EPKC(SC)是否成立,验证通过后,TTP产生唯一的序列号sn并记录到数据库中ꎻ
3)TTP对sn进行签名,然后分别使用客户的公钥和银行的公钥加密后发送给他们:

4)客户收到TTP发送的信息后,使用自己的私钥进行解密,再检验是否是由TTP生成的:
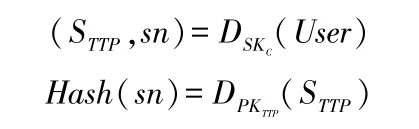
通过验证后,客户把序列号sn用于以后的电子现金货币中,银行的检验执行过程和客户一样,只是最后把序列号sn记录入数据库中,为以后查明重复支付作好准备。
3.3.2 取款
1)通过注册操作以后,客户从TTP处得到一个唯一的序列号sn,然后他就使用私钥对银行里的账户信息进行签名ꎻ随机选择一个盲因子r对sn进行盲化ꎻ再使用银行的公钥加密后发送给银行,以请求分发给合法的电子现金。
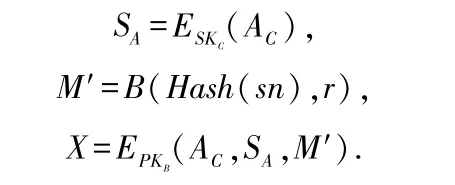
2)银行收到客户发送的X后,用私钥进行解密,再用客户的公钥检验Sa,如果结果正确,则从客户的账号中扣除电子现金,并用自己的私钥SKB对盲消息M′进行签名,再用客户的公钥加密签名后发回给客户。

3)客户使用私钥对X1进行解密,然后使用去盲函数和盲因子获得对序列号的签名。最后客户从银行获得电子现金(sn,S),但是银行不能得到除序列号外的任何信息。
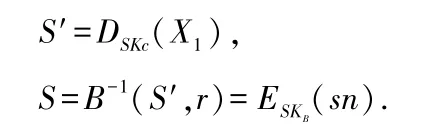
3.3.3 支付
1)客户在购买商品时,使用电子现金(sn,S)进行支付。为了获得用户想要的商家产品,客户随机产生一个数,并用私钥对进行签名,再用盲化函数和盲化因子r′实施盲化。为了安全使用商家的公钥对电子现金(sn,S)进行加密[19]。
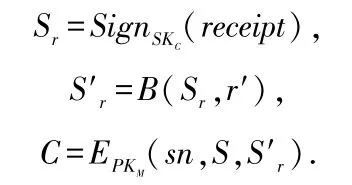
2)商家收到加密的电子现金后,用私钥解密,然后对电子现金的有效性进行检验,如果有效,则商家答应给客户商品
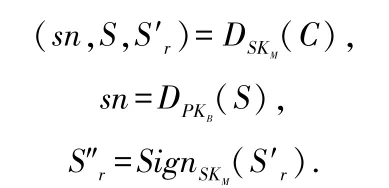
3)客户收到商家的商品和S″r后,他使用盲函数和盲因子作如下运算:

最后消费者获得了相应的商家的商品和票据,同时为了防止商家重复存储电子现金,客户要保存好收据票。
3.3.4 存款
1)商家获得电子现金(sn,S)之后,他可以存储到银行中他的账户。首先商家使用银行的公钥PKB对(sn,S)进行加密,然后再发送给银行。
2)银行获得加密的电子现金后,用私钥进行解密。最后对电子现金进行有效性检验,通过检验后增加到商家的账户中去,并对电子现进行标记,以防止重复支付[19]。
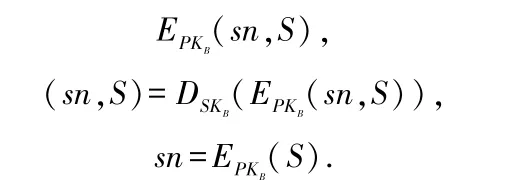
4 方案安全性分析
下面将对我们的方案中使用的协议进行详细分析,看是否符合对电子现金的各种安全性要求。
(1)防伪造性
在我们的方案中,电子现金只能由银行一家权威机构发行,而且每一个电子货币都是由银行用私钥进行签名,所以没有任何人或机构可以签名。
(2)反跟踪性
盲签名技术本身具有不可跟踪性,在撤销过程中,用户使用盲化函数和随机选择的盲化因子r对序列号sn进行了盲化,所以银行在对消息M进行签名时,不能得到任何消息内容。在商家存款过程中,银行虽然能等到有效的电子现金(sn,S),但是银行在用户和电子现金中不能得到相关信息。所以我们的方案在这点上是完全满足的。
(3)可验证性
我们的方案基于公钥密码体制,所以消费者在注册阶段能够检验出序列号sn是否由TTP产生,同时消费者也能通过银行的公钥检验出电子现金(sn,S)是否由银行产生。在支付和存储阶段也能通过银行的公钥PKB检验出电子现金是否有效。
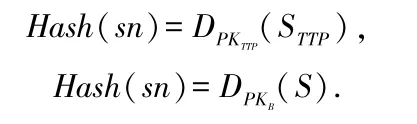
(4)防重支付
在我们的方案中,每一个电子现金都在银行数据库中有记录,而且产生的序列号sn也在TTP处均有记录。为了提高查找重复支付的效率,我们采用了部分盲签名技术,这是因为部分盲签名技术能大大减轻数据库的大小,从而提高了查找速度。银行从商家处收到想要存储的电子现金时,首先检查该电子现金是否被支付过,如果银行发现该电子现金是重复支付的,那么便联系TTP查出用户的真实身份信息IDi,很容易查出那恶意使用电子现金的消费者账户。
(5)可控性
群签名和盲签名的无条件匿名性和不可跟踪性也给犯罪分子的敲诈、拐骗、洗黑钱等活动提供了方便,所以设计一种可控性或公平的电子现金系统非常必要[17]。在Chaum方案中,由于序列号sn由消费者自己选择,也没有登记银行数据库,所以犯罪分子很容易的进行支付而不能被识别出身份。在我们的方案中,序列号sn由可信第三方TTP产生,比如由政府的金融部门担任。在我们的设计中,如果犯罪分子想从受害者处敲诈现金,由于序列号不由他自己产生,所以犯罪分子只能恐吓受害人从TTP处获取。如果受害者顺从的申请了sn′,犯罪分子获取电子现金(sn′,S′)后释放了人质,那么受害者可标识这是一个通过不正当手段获取的电子现金。当犯罪分子在商家进行消费时,商家可以报警逮捕犯罪分子,所以如果序列号是由可信第三方产生的,可以有效防止犯罪分子不受限制的消费。
5 结语
从研究的角度分析,电子现金系统的发展将会向着高效、离线、公平和安全性更强的方向发展[20]。在现有的电子现金系统方案中,大多数是基于离散对数和零知识证明等方法来构造的,那么基于大整数因子分解困难问题设计部分盲签名方案,构建公平安全的电子现金系统也是可行的研究方向。近年来,椭圆曲线密码体制以不同于其它密码体系的独特优势,成为目前的研究热点,所以,如何设计基于椭圆曲线密码体制的电子现金系统有很好的发展前景。
[1] 邱卫东,黄征,李祥学等.密码协议基础[M].北京:高等教育出版社,2009:74-92.
[2] Abe M,Fujisaki.How to Date Blind Signature.Advances in cryptology:proceedings of ASIACRYPTO′961996[C]//Heidelberg:Spring-Verlag, 1996:243-252.
[3] 蔡乐才,张仕斌,郝文化.应用密码学[M].北京:中国电子出版社,2005:201-210.
[4] Boldyeva A.Threshold Signature,Multisignatures and Blind Signature Based on the Gap-Diffie-Hellman-Group Signature Scheme.Theory and practice of public key cryptology:proceedings of PKC 2003[C]//Heidelbeg:Spring-Verlag, 2003:31-46.
[5] Wenbo Mao.Modern Cryptography:Theory and Practice[M].Pearson Education, Inc., publishing as Prentice Hall PTH,2004:206-218.
[6] 李顺东,王道顺.现代密码学:理论、方法与研究前沿[M].北京:科学出版社,2009:109-123.
[7] Chaum.Blind signatures for untraceable payments[J].In Advances in Cryptology Proceedings of CRYPTO′82,Plenum,New York, 1982,21(2):199–170.
[8] Chaum, Fiat, and Naor.Untraceable electronic cash.In S.Goldwasser.Proceedings on Advances in Cryptology(Santa Barbara, California, United States)[C]//New York, Springer-Verlag 1988:319-327.
[9] T.Okamoto,K.Ohta.Universal Electronic Cash[C]//Proceedings of CRYPTO′91,LNCS 576.Germany:Springer-Verlag,1993:324-337.
[10] Brands S.An efficient off-line cash system based on the representation problem[R].Netherlands:CWITechnical Report CS-R9323,1993.
[11] M.Stadler,ect.Fair Blind Signature[C]//In Advances in Cryptology – EUROCRYPTO′95, LNCS 921.Germany:Springer-Verlag, 1995:209-219.
[12] E.Brickell, D.Gemmell, D.Kravitz.Trustee-based tracing extensions to anonymous cash and the making of anonymous change[C]//In proceedings of the 6th Annual ACM-SIAM Symposium on Discrete Algorithms.Germany:Springer-Ver-lag,1995:157-166.
[13] Frankel Y,Tsiounis Y,Yung M.Indirect discourse proofs:Achieving fair off-line e-cash[C]//Proc.of ASIACRYPTO′96.German:Springer-Verlag,1996:286-300.
[14] Davida D, Tsiounis Y,Yung M.Anonymity control in e-cash systems[C]//CRYPTO′97 proceedings, LNCS 576.Germany:Springer,1997:224-230.
[15] Frankel Y,Tsiounis Y,Yung M.Fair off-line e-cash made casy[C]//Proc.of ASIACRYPTO′98.Germany:Springer-Verlag,1998:386-396.
[16] Lysyanskaya, Anna, Zulfikar Ramzan.Group blind digital signatures:A scalable solution to electronic cash[C]//Financial Cryptography ′98, LNCS 1465.Berlin:Springer-Verlag,1998:184 – 197.
[17] 杨波,刘胜利.利用Smart卡的可撤销匿名性的电子支付系统[J].电子学报,1999(6):83-86.
[18] 关振胜.公钥基础设施PKI及其应用[M].北京:电子工业出版社,2008:389-414.
[19] 李洪心.电子商务安全[M].大连:东北财经大学出版社,2012:152-163.
[20] 杨浩淼.快速产生安全椭圆曲线的研究[D].西安:西安电子科技大学,2013:40-50.
