基于有限元法的特高压输电线路三维工频电场仿真

基于有限元法的特高压输电线路三维工频电场仿真

严孝顺1方福歆2孔海洋2王璇2

(1.国网安徽省电力公司安庆供电公司，安徽 安庆 246003；2.武汉大学电气工程学院，湖北 武汉 430072)

摘要：为了研究1 000 kV特高压交流输电线路周围的工频电场分布，基于有限元法，运用Ansoft Maxwell仿真软件，在Maxwell 3D瞬态电场的求解环境下搭建了线路三维仿真模型，手动剖分了基于圆柱体的导线模型，同时为其加载了三相同相序电压，计算得到不同时刻下线路下方距地面1.5 m处的场强。其中，当边相导线对地高度为24 m时，在0.003 358 s这一时刻得到了指定路径最大场强值3 400 V/m。改变边相导线对地高度，得到线路对地高度不同时地面场强的变化趋势：随着输电线路对地高度的不断增加，距地面1.5 m处的场强不断减小。

关键词：特高压输电线路；有限元法；三维工频电场仿真

收稿日期:2015-05-15

作者简介：严孝顺(1984—)，男，安徽枞阳人，助理工程师，研究方向：电力系统及其自动化。

0引言

特高压交流输电具有容量大、距离远、损耗低、占地省等显著优势，有利于建立坚强的电网和解决短路电流过大超过开关容量极限的问题，是解决我国电网和能源发展难题的重要选择[1]。随着我国特高压交流输电线路建设步伐的日益加快，线路周围的电磁环境已成为人们日益关注的话题，主要包括：工频电场及静电感应、工频磁场及电磁感应、无线电干扰、电视干扰、可听噪声[2]。而在这其中，线路下方距地面1.5 m处的场强又是决定线路走廊宽度和地面最大场强的重要依据，因此，本文基于有限元分析方法，通过Ansoft Maxwell仿真软件搭建线路模型，具体分析了不同时刻线路下方距地面1.5 m处的场强变化以及线路边相导线对地距离的不同所导致的场强变化规律。

1计算方法简述

有限元法的基本特点是分块近似，它将所要分析的连续场域分割为很多较小的单元体，这些单元体的集合就形成了原来的场域整体。它着眼于建立每一个单元体的计算公式，并将它们累加组合起来，从而求得连续场的近似解。从数学角度来看，有限元法以变分原理为基础，通过区域剖分和分片插值，把二次泛函的极值问题转化为一般多元函数的极值问题，而后者又等价为一组多元线性代数方程的求解[3]。

而Ansoft Maxwell正是基于有限元法的低频电磁场仿真软件，在三维场下，基于四面体剖分单元的插值基函数如下：

从而：

泊松方程可书写为如下形式：

(1)

采用变分法将式(1)离散，得到总的系统方程如下：

SU=F

(2)

其中系数矩阵由各单元相应项组合得到，表达式如下：

S=[Sij]

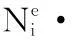
式(2)右端项同样也是由各单元项组合得到：

在三维电场求解器中，以标量电位作为待求量，并配以正确的边界条件作为定解条件。三维电场满足下式：

▽·(εr·ε0▽Φ)=-ρv

(3)

式中，Φ(x，y，z)为三维标量电位；εr(x，y，z)为3个方向矢量上的相对介电常数；ε0为真空介电常数；ρv(x，y，z)为体电荷密度[4]。

一旦得到Φ，可由麦克斯韦微分方程组直接得到电场强度E和电位移矢量D，这两个基本场量可由式(4)计算得到：

(4)

电流密度J也可由三维标量电位计算得到，如式(5)所示：

J=σ(x，y，z)·E=σ(x，y，z)·(-▽Φ)

(5)

本次仿真实验所选择的求解类型是Maxwell 3D瞬态电场，其边界条件只包含绝缘边界条件、对称边界条件及主从边界条件，而不含有Maxwell 2D中可以求解无穷远空间的气球边界条件，故只能人工划定求解空间和求解域，不可避免地会产生截断误差。但由于输电线路结构简单，容易剖分且边界可取得很大，截断误差可控制在工程计算所需精度要求之内[5]。

根据文献[6]，输电线路的悬链线方程为：

(6)

在等高跨接情况下：

式中，yB为杆塔绝缘子下导线悬挂点的高度；D为相邻两杆塔悬挂点之间的水平距离。

经过实际绘图及计算发现，当线路档距很大时，其弧垂最低处可近似看作与地面平行。结合上述分析及文献[7]，可对本文的建模作如下简化：(1) 弧垂处导线为与地面平行的光滑圆柱体；(2) 忽略杆塔等邻近物体的影响，忽略导线的端部效应和弧垂影响。

2仿真模型建立

2.1基本参数设定

杆塔类型参照文献[8]进行选择，即1 000 kV单回路“M”型杆塔。三相线路水平排列，相间水平距离设定为10 m。导线选用8分裂LGJ-500/45，A、B、C三相的电压依次取：

2.2建立模型

在Maxwell 3D瞬态电场环境下，以xoy面为大地平面，依据导线参数绘制三相线路。边相导线对地高度依次设定为22 m、24 m、26 m，中间相始终高于边相3.3 m。大地平面上方绘制40 m×80 m×40 m的长方体空气域，大地平面下方绘制40 m×80 m×5 m的长方体土壤域，土壤电导率设定为0.01 S/m。最外层为求解域，设定为20%外扩。绘制宽2 m、长60 m的带状求解区域，距xoy面1.5 m，同时设置此区域平行于x轴的中心线为指定路径，从而可在后处理中得到线路下方距地面1.5 m处的场强分布。

具体模型如图1所示。

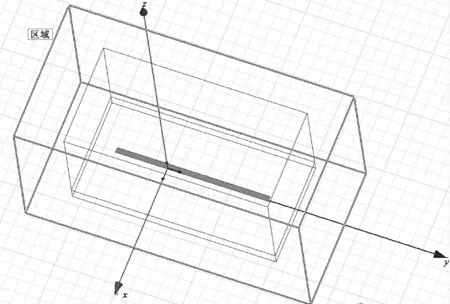
图1　1 000 kV交流特高压输电线路场强分布模型

对模型进行手动剖分。空气域、土壤域、求解域的单元最大长度设定为4 m，导线单元最大长度也设定为4 m，对于圆柱曲面还要进一步剖分，圆内三角形最大弦长设置为0.28 m，弦所对应三角形内角角度设置为20°，外接圆半径与3倍内接圆半径的比值设置为0.6。模型剖分结果如图2所示。

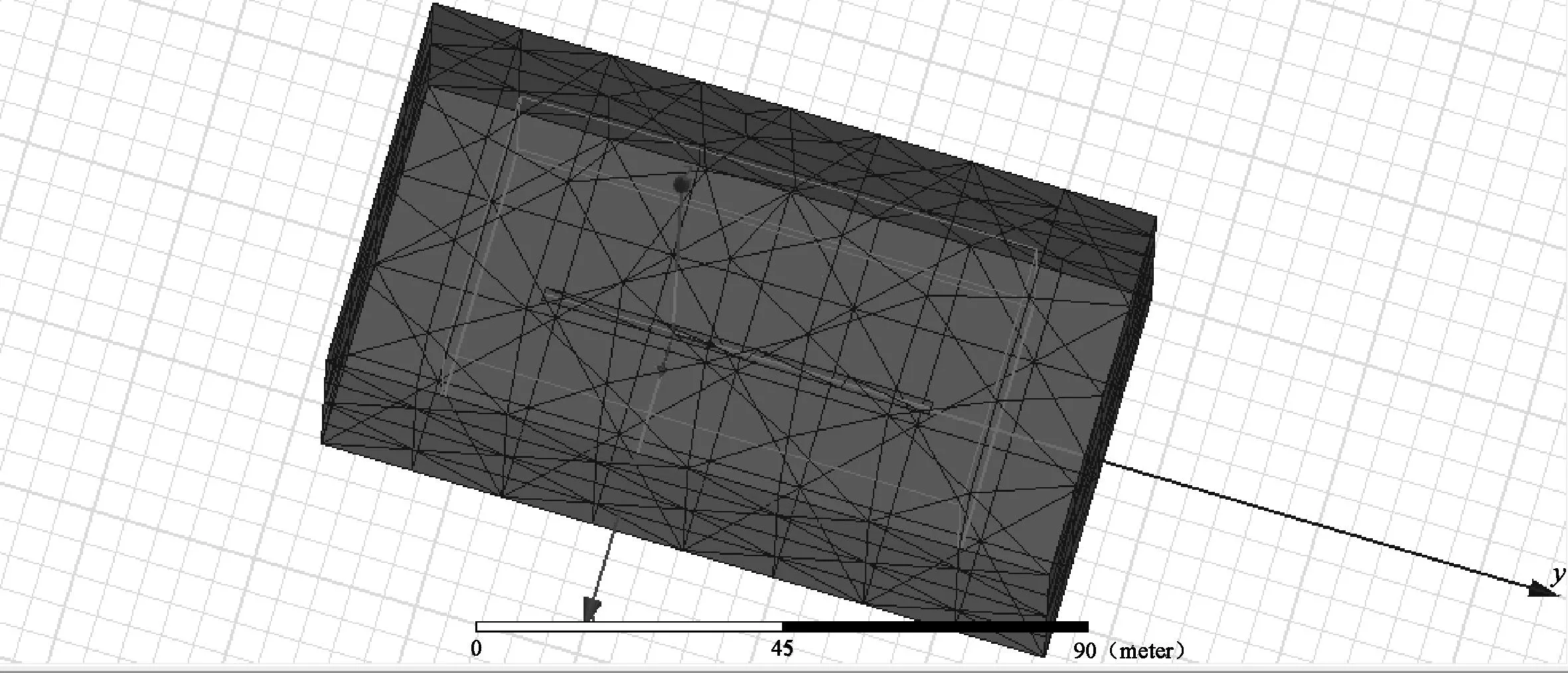
图2　模型剖分

在求解设置中，以周期时长0.02 s为计算周期，最大间隔时间设置为0.005 s。

3仿真结果分析

3.1不同时刻场强分布分析

以对地高度24 m为例，取0 s、6.404 8e-009 s、0.003 358 s、0.006 715 9 s、0.011 716 s、0.016 716 s、0.02 s 7个时间节点(依次编号为1、2、3、4、5、6、7) 进行分析讨论。各时刻场强值分布如表1所示(线路中间相横轴坐标为30 m)。

表1　对地高度24 m时不同时刻场强及其坐标

由表1可看出，0.003 358 s这一时刻有最大场强值3 400 V/m，但其没有超过国标规定的4 kV/m场强限值。这一时刻对应的场强分布云图及指定路径场强分布图如图3、4所示。

图3　0.003 358 s时刻场强分布云图(24 m)

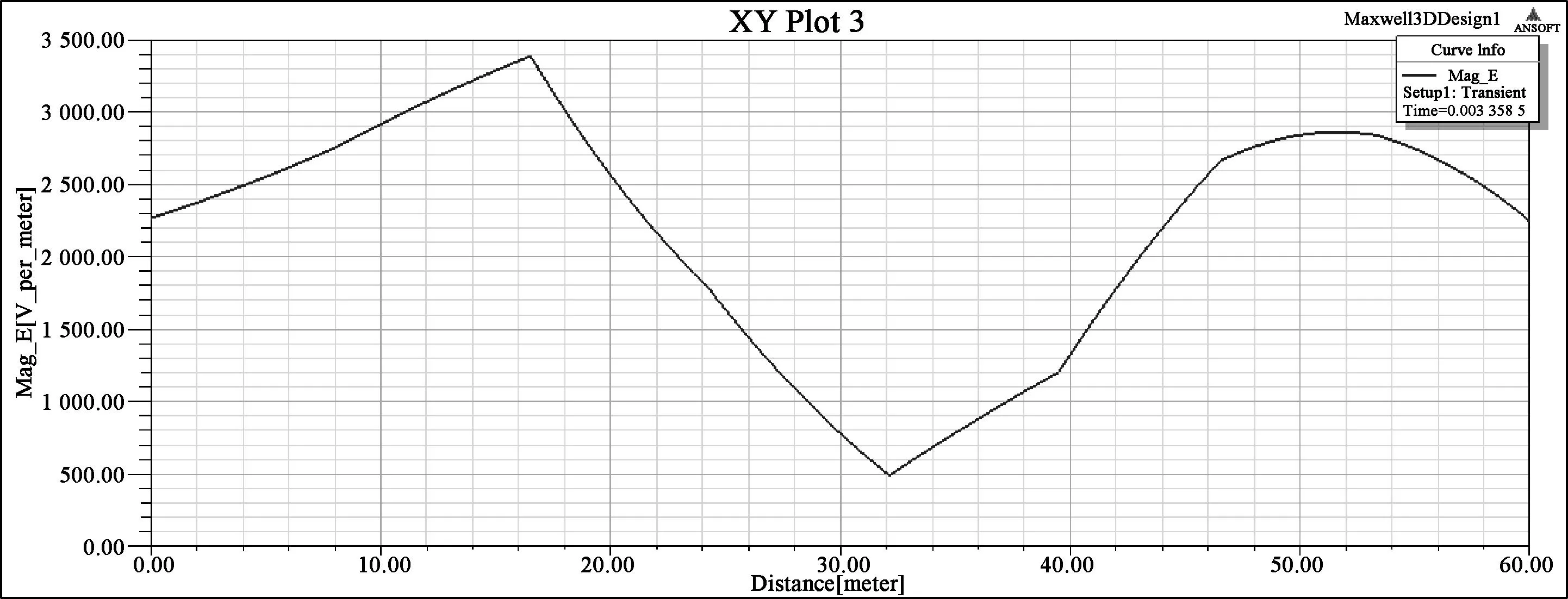
图4　0.003 358 s时刻指定路径场强分布图(24 m)

由表1还可发现，距地面1.5 m处的场强随时间呈现出类似正弦的变化规律，这与输电线路交变电压相吻合。

3.2对地高度不同时场强分布分析

继续取时刻0.003 358 s进行分析。图5～8是对地高度分别为22 m、26 m时，距地面1.5 m处的场强计算结果图。

图5　0.003 358 s时刻场强分布云图(22 m)

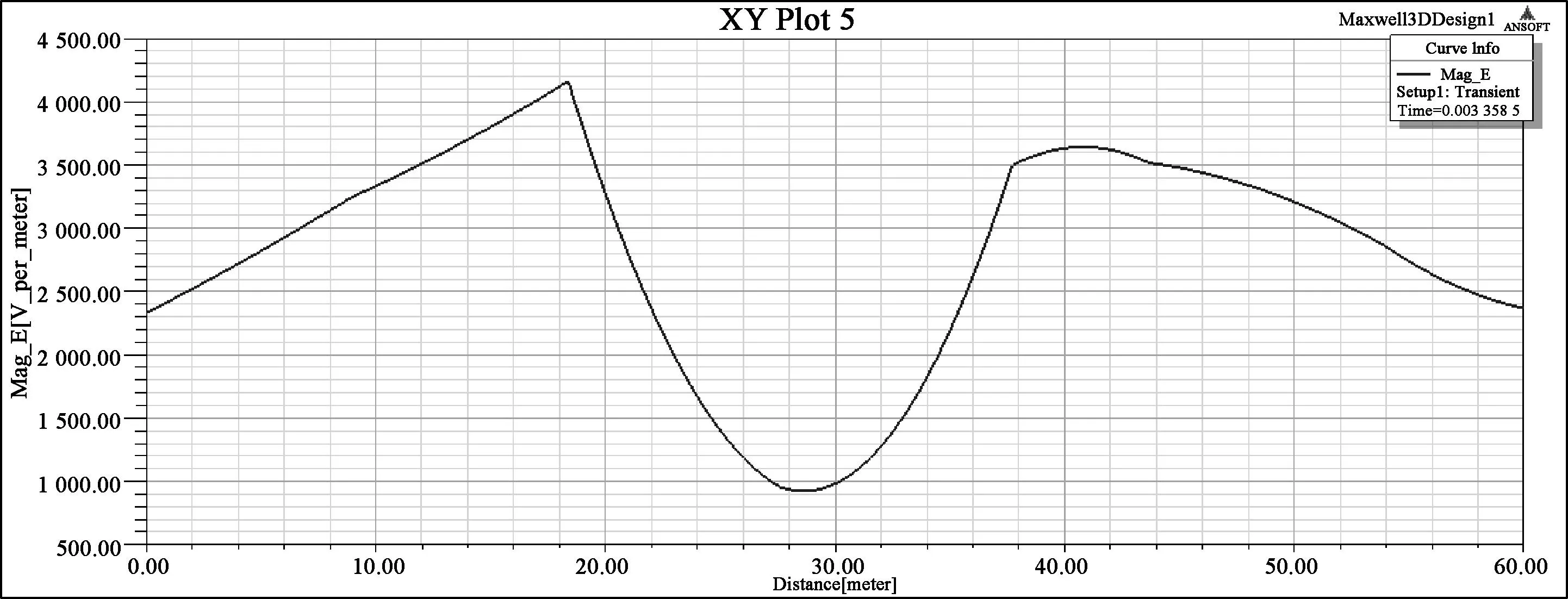
图6　0.003 358 s时刻指定路径场强分布图(22 m)

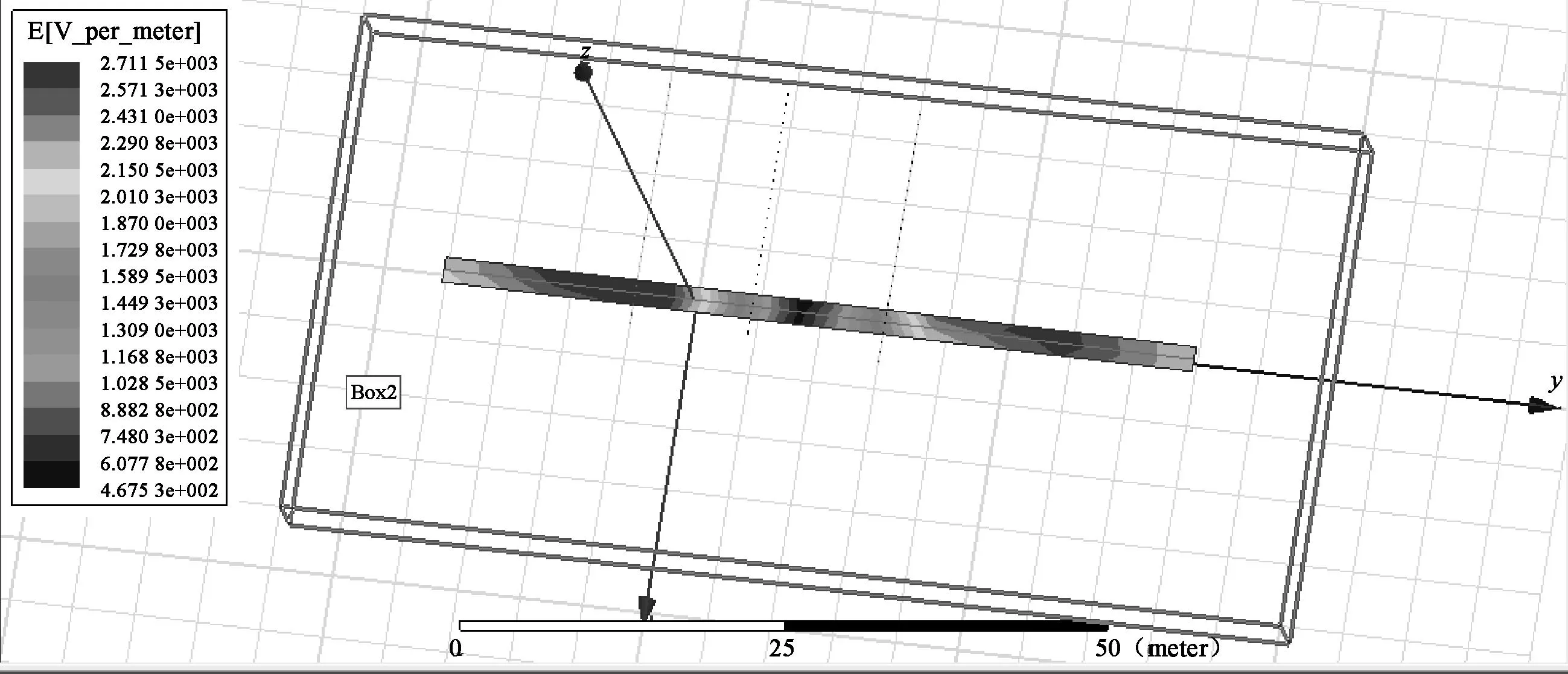
图7　0.003 358 s时刻场强分布云图(26 m)

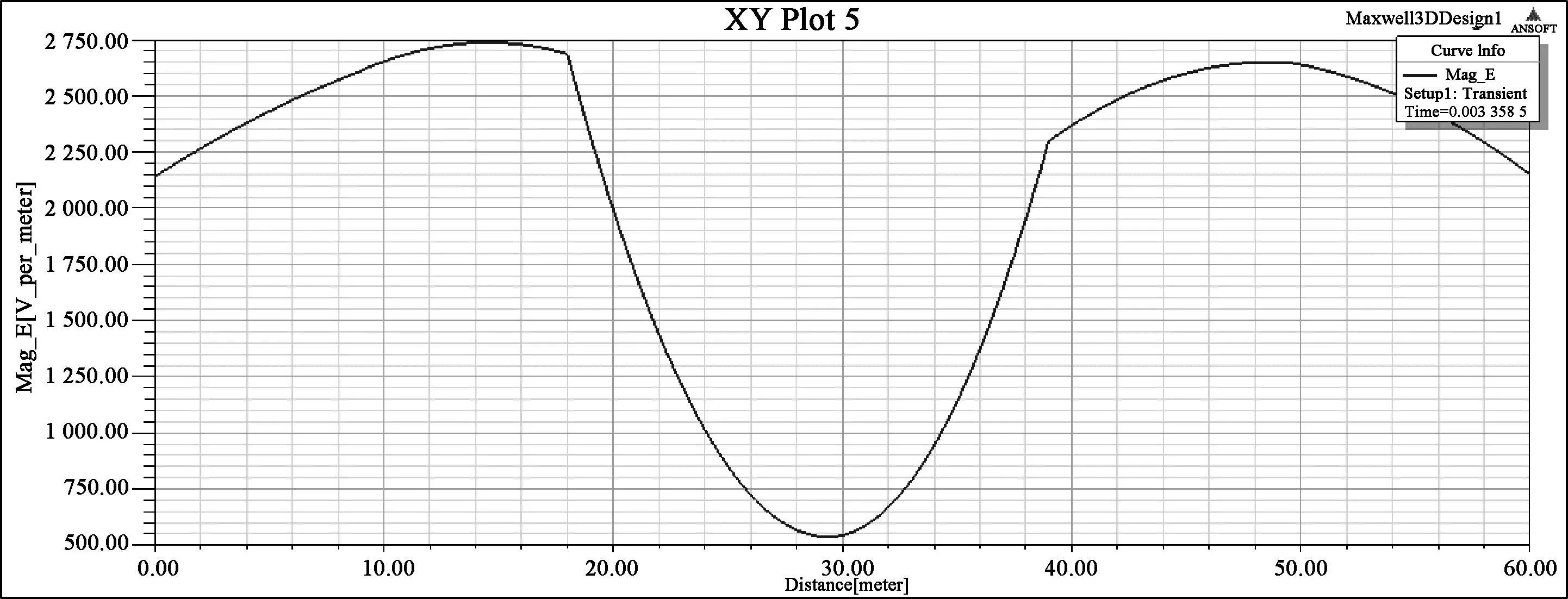
图8　0.003 358 s时刻指定路径场强分布图(26 m)

根据以上结果，对比3.1的结果，列出表2。

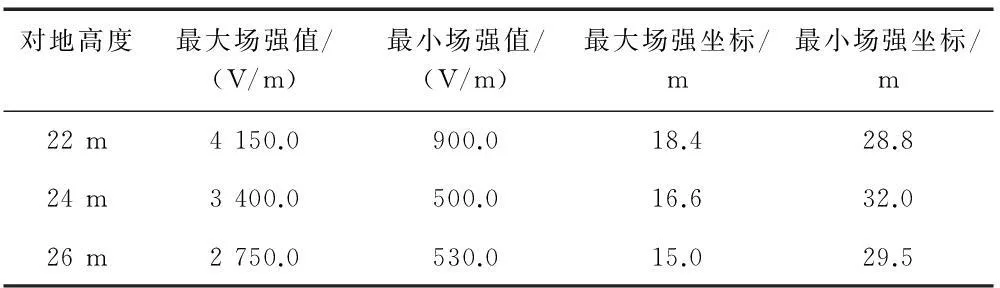
表2　0.003 358 s时刻不同对地高度场强分布表

从表2可看出，对地高度22 m时，场强最大值4 150.0 V/m不满足国标要求；距离提高至24 m后，便可完全满足要求，且随着输电线路对地高度的不断增加，距地面1.5 m处的场强在不断减小。

与此同时，综合表1及表2的坐标数据可以发现，场强最小值几乎都出现在线路中间相正下方左近，而场强最大值距离边相导线不超过5 m。

4结论

(1) 本文运用基于有限元法的Ansoft Maxwell仿真软件搭建的三维线路模型，用于计算距地面1.5 m处的场强是十分有效的。

(2) 在模型搭建过程中，输电线路交变电压的考虑很必要，不同时刻对应的叠加场强必然不同，找到各时刻的最大场强，便可基于国标进行分析论证。

(3) 输电线路的对地高度对于距地面1.5 m处场强的影响很大，且边相导线两侧距地面1.5 m处场强的变化规律是：距边相导线越远，场强越小。

(4) 本模型的剖分精度不是特别高，可根据自身的设备条件进行更高精度的手动剖分，以获得更为精确的仿真结果。

(5) 本模型没有考虑杆塔及附近房屋的影响，可在进一步的研究中考虑这些因素，得到更加逼近实际的仿真结果。

[参考文献]

[1]吴敬儒，徐永禧.我国特高压交流输电发展前景[J].电网技术，2005，29(3)： 1-4.

[2] 邬雄.特高压输电的电磁环境问题研究[J].电力系统通信，2006，27(164)： 1-5.

[3] 杨宪章.工程电磁场[M].2版.北京：中国电力出版社，2011：181-185.

[4] 赵博，张洪亮.Ansoft 12在工程电磁场中的应用[M].北京：中国水利水电出版社，2010：216-224.

[5] 苏国政，黄道春，余世峰，等.特高压紧凑型输电线路工频电场强度计算[J].武汉大学学报：工学版，2007，40(3)： 99-102.

[6] 姜广智.悬链线方程在高压架空输电线路中的应用[J].科学技术与工程，2008，8(8)： 1960-1964.

[7] IEEE Corona and Field Effects Subcommittee Report，Radio Noise Working Group．A survey of methods for calculating transmission line conductor surface gradients[J]．IEEE Trans.PAS，1979，98(6)： 1996-2007.

[8] 彭迎，阮江军.模拟电荷法计算特高压架空线路三维工频电场[J].高电压技术，2006，32(12)： 69-73.