基于故障演化分析的齿轮故障预测特征选择



基于故障演化分析的齿轮故障预测特征选择

傅鹏程1，2，王昌明1，段俊斌2，谭晓栋3

1)南京理工大学机械工程学院，南京210094; 2)北京特种机电技术研究所，北京100012;

3)武警警官学院电子技术系，成都610213

摘要:提出基于故障演化分析的齿轮故障预测特征选择方法．根据机械动力学与振动模型，计算不同故障严重程度下系统的输出响应．使用特征选择方法建立不同特征描述的齿轮故障演化曲线，计算各特征对齿轮故障演化过程的跟踪能力，选择跟踪能力最大的特征作为故障预测特征．以一阶齿轮传动系统的齿轮裂纹故障为例，论证结果表明，小波熵对齿轮裂纹故障演化过程的跟踪能力最大，采用小波熵作为齿轮裂纹故障的预测特征能有效提高故障预测的精度．

关键词:机械动力学与振动;齿轮;特征选择;故障预测;故障演化分析;跟踪能力;小波熵

Received: 2015-01-25; Revised: 2015-05-22; Accepted: 2015-06-15

Foundation: The Specialized Research Fund for the Doctoral Program of Higher Education(20133219110027)

Corresponding author: Senior engineer Fu Pengcheng．E-mail: fang820729@ sina.com

Citation: Fu Pengchen，Wang Changming，Duan Junbin，et al．A feature selection for fault prognosis based on fault evolution analysis［J］．Journal of Shenzhen University Science and Engineering，2015，32(4) : 434-440．(in Chinese)

故障预测技术对有效避免处于工作状态的部件因突然失效而导致灾难性事故的发生具有重要意义［1］．故障预测特征选择方法是实现故障预测功能的关键，它决定了故障预测的准确和有效［2-3］．目前，常用的故障特征选择方法主要有时域法(如均方根、峰态因子、能量比、峭度和标准差等)，频域法(傅里叶变换和快速傅里叶变换等)，以及时-频域法(如Gabor变换和小波变换等)［4］，采用这些故障特征选择方法主要侧重两方面:一是从较强环境噪声中提取区别于正常状态的故障特征，以驱动故障报警;二是从强背景噪声中提取机电系统中不同故障的特征，为故障诊断或识别提供数据输入．故障预测特征提取是指从复杂的背景噪声中提取有用的包含表征故障严重程度的特征信息，这些信息能有效描述故障的演化趋势，为故障预测提供有效输入的一种特征选择方法［5］．研究证明，故障预测特征能否有效描述故障的演化趋势，直接影响故障预测结果的有效性和可行性［6-7］．因此，选择一个有效的故障预测特征，对提高机电系统故障预测技术的效率和准确性具有重要意义．

在齿轮传动系统中，存在很多具有缓变故障特性的部件，故障从早期微弱特征逐渐加剧直至演变为完全失效会经历一个故障演化过程．对任何一种故障预测技术而言，为其提供输入信息的故障特征必须具有两个功能:①能尽早且更敏感反映故障早期微弱状态;②能敏感反映故障的演化过程［6］．因此，本研究通过分析齿轮故障的演化趋势，同时考虑演化趋势的单调性和敏感性两方面，定义一个量化指标，即特征对故障演化的可跟踪能力，以此衡量特征对齿轮故障预测技术的支持能力，进而提出基于故障演化分析的齿轮故障预测特征选择方法．以包括电机、齿轮和轴承等典型机械部件的传统齿轮系统为例，对本方法进行了验证．

1　齿轮故障演化分析

在实际工程中，由于受人为因素、背景噪声、测试仪器精度和机器运转过程的固有属性等因素影响，采用特征值描述的故障演化趋势不是完全单调变化的．如描述机械部件全寿命过程的浴盆曲线，如图1［8］．浴盆曲线主要包括早期失效期、偶然失效期和耗损失效期3个阶段．早期失效是由于产品设计、原材料和制造过程中的缺陷造成的，一般在试运行前通过试验剔除不合格品;偶然失效期失效率较低，且较稳定，往往可近似看作常数，该时期是产品的良好使用阶段;耗损失效期是由于产品的长时间使用，磨损、疲劳、老化和耗损等原因造成，产品从故障程度逐渐加剧到功能失效．在这段时间里，产品性能的退化趋势是单调的，耗损失效期本质上是一个理想的故障演化过程．为避免由于早期故障的逐步加剧或演化导致产品功能失效事件的发生，本研究主要分析耗损失效期故障特征对早期故障的检测能力和对故障演化过程的跟踪能力，忽略浴盆曲线中部件从正常状态经历的早期失效期和偶然失效期两个阶段，研究主要集中在产品性能开始退化直至功能失效的故障演化过程，特征对故障演化的描述能力．

图1　全寿命过程浴盆曲线［8］Fig.1 The bathtub curve［8］

对该过程而言，随着故障程度的加剧，描述齿轮性能退化程度的预测特征值呈单调递增趋势，表示齿轮故障严重程度(退化量d)会随时间的延长而增大．图2为某预测特征描述的齿轮故障演化趋势曲线(t)．其中，t为运行时间; tI为早期故障发生时间; tTTD为预测特征器或者检测系统检测到早期故障状态的时间; tTTF为故障增长到预定的失效阈值的时间; DF为预定的失效阈值; DI为早期故障阈值;Δd为预测特征描述的退化值的变化量; Δf(Δt)为Δt时刻内故障严重程度的变化量．

图2　故障演化分析的相关定义Fig.2 The related definitions of fault evolution analysis

时效性的表达式为

tSFDT既与齿轮故障从早期微弱状态到最终失效的演化时间有关，又与所选择预测特征的预警故障的时间和能力有关．tSFDT值越小，说明从故障的发生到被检测到的时间越短，确保了在完全失效前实现健康状态评估;反之，tSFDT值越大，表明该预测特征手段预警该故障时间越长．如果tSFDT≥1，则说明在该故障模式演变成完全失效后才能被检测到，此时故障预测已毫无意义．

同时，对于一个具有明显征兆变化的齿轮渐变故障，所选择的预测特征手段对该故障变化量的检测能力定义为

在实际工程中，即使采用相同的传感器或检测手段监控齿轮同一个故障的演化过程，提取不同的预测特征所表征的故障演化趋势会出现很大的不同．图3为两种预测特征手段所描述的故障演化趋势曲线．其中，tTTD_1与tTTD_2分别为预测特征手段1和特征手段2对早期故障的预警时间;Δd1与Δd2分别为特征手段1和特征手段2描述故障程度在Δt时间内的变量;Δf(Δt)为Δt时间内故障严重程度的变化量．从图3可见，tTTD_1＜tTTD_2，说明预测特征手段1能以更快时间检测到早期故障状态;Δd1＞Δd2，说明在Δt时间内特征手段1对故障变化的灵敏度要高于特征手段2．

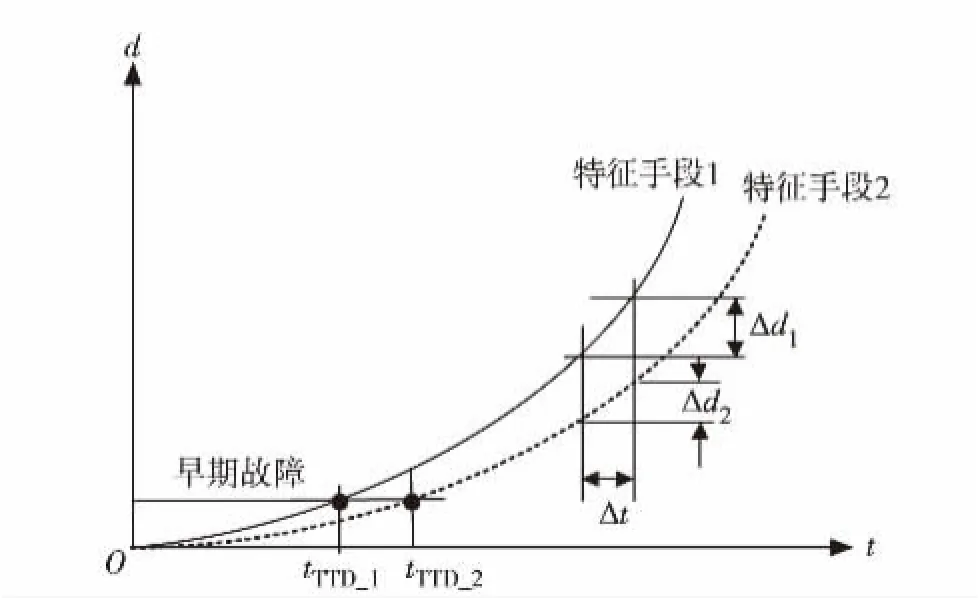
图3　两种预测特征手段描述的故障演化趋势曲线Fig.3 The fault evolution trend curves of two features for fault prognosis

2　基于故障演化分析的预测特征选择

基于以上对齿轮故障的演化趋势分析，考虑特征描述故障演化趋势的单调性和敏感性，本研究定义特征对故障演化的可跟踪能力这一量化指标来衡量特征对故障预测的贡献水平，提出基于故障演化分析的齿轮故障预测特征选择策略，流程如图4．

图4　故障预测特征选择流程图Fig.4 The flowchart of feature selection for fault prognosis

基于故障演化分析的齿轮故障预测特征选择策略为:

步骤1建立系统的损伤动力学模型，获取齿轮从正常状态、早期故障状态到完全失效状态整个故障演化过程中，不同故障严重程度状态下系统的输出响应．

步骤2采用现有的故障特征选择方法，得到故障特征集合S = { s1，s2，…，si，…，sM}．其中，si为第i个特征; M为故障特征的总数．建立各种特征描述的齿轮故障演化趋势曲线．同时计算预测特征si描述的故障演化趋势i的单调统计值为其中，i(n1)和i(n2)分别为趋势曲线i在n1和n2时刻对应的特征值; sign()为符号函数; N为故障特征si描述故障演化趋势曲线i所有观测点的总数．

特征si描述的故障演化趋势曲线的单调性水平为si对故障演化趋势的总敏感度水平为

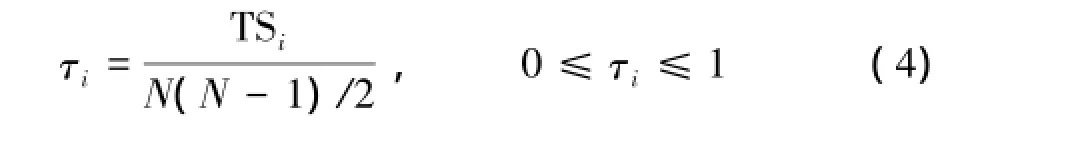
其中，函数median（）用于求解括号内趋势系列的中值；ϕi（1）为无故障状态时的特征输出值；d（n1）和d（n2）分别为n1及n2时刻故障的严重程度；ϕi（n1）和ϕi（n2）分别为趋势曲线ϕi在n1和n2时刻对应的特征值．

步骤3 分析各种特征描述的故障演化趋势，计算各特征对故障演化过程的跟踪能力．参考Lyu等［6］和Zhang［9］提出的故障检测能力，定义特征si为

其中，τi为si描述的故障演化趋势曲线的单调性水平；βi为第i个特征si对故障演化趋势总的敏感度水平．τi或βi越大，特征si对故障演化过程的跟踪能力TFFi越大．TFFi综合考虑了特征对其描述的故障演化过程的单调性水平和灵敏度水平，衡量了一个特征对故障演化过程的跟踪能力．

步骤4 选择对故障演化过程跟踪能力最大的特征作为故障预测特征s∗，其表达式为

其中，S为所有的预测特征集合．

3　案例分析

以一阶齿轮箱系统为例，验证本方法的有效性和可行性．图5（a）为直齿轮箱的简化模型，图5 （b）为直齿轮箱的等效模型．其中，y1和y2分别为主动和被动齿轮在y轴向的线位移；θ1和θ2分别为主动和被动齿轮在y轴向的角位移；θm和θb分别为驱动电机和负载的角位移；T1和T2分别为驱动电机的输入力矩和负载的输出力矩；m1和m2分别为主动和被动齿轮的质量；k（t）为正常状态（无故障）齿轮的啮合刚度；kp和kg分别为柔性连接件的扭转刚度；k1和k2分别为输入和输出轴承的径向刚度；c（t）为啮合的阻尼系数；cp和cg分别为输入和输出柔性连接件的阻尼系数；c1和c2分别为输入和输出轴承的径向粘性阻尼系数；Im和Ib分别为驱动电机和负载的转动惯量；I1和I2分别为主动和被动齿轮的转动惯量；Rb1和Rb2分别为主动和被动齿轮的基圆半径．

图5　一阶齿轮箱系统模型FigƱ 5 A one⁃stage gearbox system

为了简化，本研究仅考虑齿轮箱系统的齿轮裂纹故障，建立系统包含裂纹损伤的损伤动力学模型为

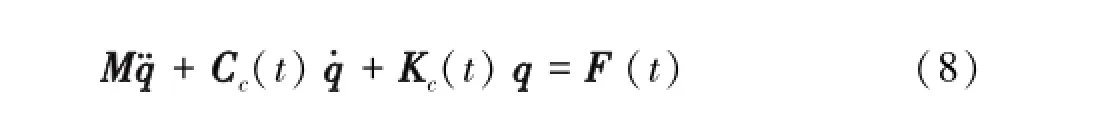
其中，M为系统质量矩阵；q为广义位移向量，q＝［y1y2θ1θ2θmθb］；q·为广义速度向量；q¨为广义加速度向量；Cc（t）和Kc（t）分别为损伤齿轮的阻尼系数矩阵和刚度矩阵；F（t）为外部激励，参数设置见文献［10］．

齿轮的裂纹等损伤会影响齿轮的几何参数和啮合刚度．由于齿轮初期裂纹大小相对齿轮的几何尺寸来说很小，因此，本研究仅考虑齿轮裂纹故障对啮合刚度的影响．齿轮出现裂纹损伤会直接导致齿轮的啮合刚度降低［6，10］．同时，由于啮合刚度作为齿轮损伤动力学模型中的主要参数，因此，在齿轮运转过程中，啮合刚度降低会使齿轮的输出参数，如径向位移、速度和加速度，以及齿轮的输出扭矩等参数发生变化，本研究基于该原理建立齿轮裂纹故障与输出参数间的关系．

图6为齿轮正常状态和裂纹损伤0Ʊ 05程度下的

图6　齿轮正常状态和裂纹损伤0.05时的齿轮啮合刚度Fig.6 The time-varying mesh stiffness with normal state and tooth crack level 0.05

齿轮啮合刚度．通过调节式(8)中齿轮的啮合刚度可仿真齿轮不同裂纹损伤下系统的动力学响应，如式(9)至式(12)．

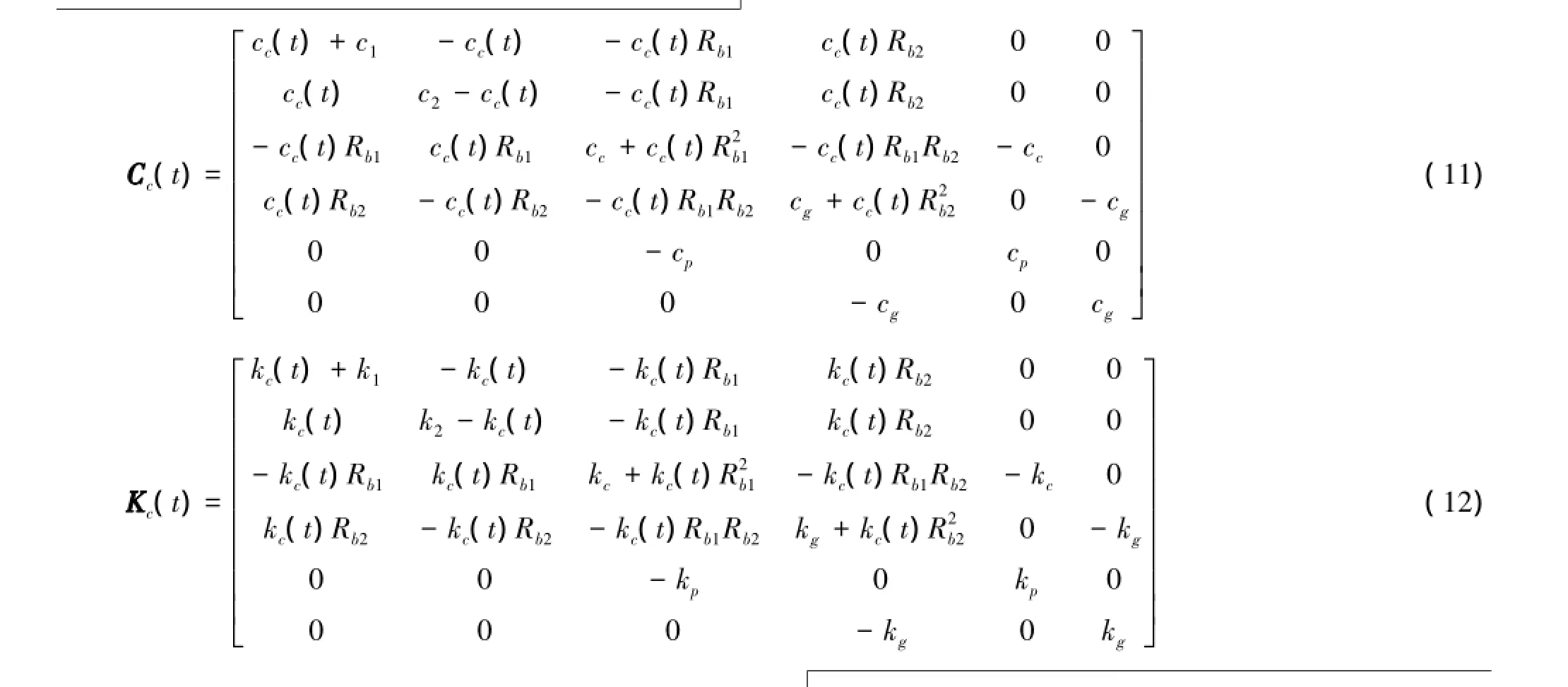
设置齿轮裂纹故障严重程度d(0≤d≤1)从0 到50%以5%的步长递增，采用Matlab软件的ODE15求解器进行求解，可获得齿轮裂纹故障严重程度从0到50%主动齿轮线加速度a1的响应．图7展示了齿轮裂纹故障严重程度s分别为0、10%、20%、30%、40%和50%状态下，主动轮齿的角加速度a1的响应输出曲线．

在工程实际中，齿轮的故障信号包含了较强的背景噪声，因此，需要从噪声干扰的信号中提取故障特征信息［5］．均方根代表了振动信号的能量，能很好的描述齿轮从正常状态到裂纹逐渐加剧整个故障演化过程中振动能量的变化，随着裂纹程度增加，均方根值渐增;峭度用来描述齿轮振动信号分布函数的陡峭程度，齿轮损伤越大，峭度值越大［5］;小波熵描述故障齿轮在不同频率段能量分布的均匀程度，故障越严重，小波熵越大［6］;故障增长参数(fault growth parameter，FGP)描述了齿轮振动信号的模极大值偏离平均值的程度，齿轮故障越严重，则FGP值越大［11-12］．这4个指标能很好地描述齿轮裂纹故障演化的趋势，是提高故障预测精度最重要的因素之一．当然，工程中还有很多用于提取齿轮裂纹故障特征的参数，如倒谱、复合谱和全谱等，这些参数大多用于故障的检测和识别诊断，以及早期故障诊断等领域，但这些参数不能有效描述故障的演化的趋势．因此，本研究仅选择均方根、峭度、小波熵和FGP这4种特征参数来验证本方法的有效性．

图7　不同齿轮裂纹故障程度下a1的响应曲线Fig.7 The responses of a1with the different crack levels

为了简化，本研究采用工程中常用的均方根、峭度、小波熵和FGP四种特征选择方法［6］，计算各特征随齿轮裂纹故障渐增的变化趋势．为便于对比，本研究将各个特征指标进行了归一化处理(记为s*N)，并建立了4个特征描述的齿轮裂纹故障的演化趋势，结果如图8．

使用式(4)和式(5)分别计算4个特征描述的裂纹故障演化趋势曲线的单调性水平τi和灵敏度水平βi，结果如表1．从表1可见，小波熵和FGP描述的齿轮裂纹故障的演化趋势的单调性程度最大为1.000 0，说明小波熵和故障增长FGP描述的齿轮裂纹故障演化呈完全单调递增的趋势．然而，在4个特征中，小波熵对早期裂纹故障的灵敏度最大，为9.948 3，表明小波熵能更早且更敏感的检测出齿轮裂纹的早期故障状态．据此，采用式(6)，可分别计得4个特征对裂纹故障演化过程的跟踪能力TFFi，如表1．显然，小波熵对裂纹故障演化过程跟踪能力为0.993 3，在4个特征中最大．因此，选择小波熵作为裂纹故障的预测特征．

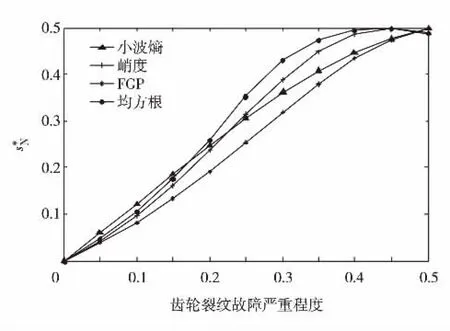
图8　四种特征描述的齿轮裂纹故障演化趋势Fig.8 The fault evolution curves described by four fault features

表1　τi、βi和TFFi计算结果Table 1 The results of τi、βiand TFFi

结语

齿轮从正常状态到功能失效状态会经历一个故障严重程度逐渐加剧的演化过程．跟踪和监控齿轮故障演化过程对指导齿轮故障预测具有重要意义．本研究以齿轮故障演化分析理论为基础，采用工程中常用的特征提取法建立齿轮裂纹的故障演化趋势．在此基础上，计算特征对裂纹故障演化的跟踪能力，并选择对裂纹故障演化过程的跟踪能力最大的特征作为裂纹故障预测的特征．仿真案例分析结果证明，在均方根、峭度、小波熵和FGP四个工程中常用的齿轮故障特征中，小波熵对裂纹故障演化过程的跟踪能力最大，可将小波熵作为齿轮裂纹故障的预测特征．本研究提出的方法也为其他机电系统缓变故障预测特征选择提供了参考．

引文:傅鹏程，王昌明，段俊斌，等．基于故障演化分析的齿轮故障预测特征选择［J］．深圳大学学报理工版，2015，32(4) : 434-440．

参考文献/References:

［1］Dong Ming，He D．A segmental hidden semi-Markov model based diagnosis framework and methodology［J］．Mechanical Systems and Signal Processing，2007，21(5) : 2248-2266．

［2］Medjaher K，Camci F，Zerhouni N．Feature extraction and evaluation for health assessment and failure prognostics ［C］//Proceedings of First European Conference of the Prognostics and Health Management Society．Dresden(Germany) :［s．n．］，2012: 111-116．

［3］Bin G F，Gao J J，Li X J，et al．Early fault diagnosis of rotating machinery based on wavelet packets: empirical mode decomposition feature extraction and neural network ［J］．Mechanical Systems and Signal Processing，2012，27: 696-711．

［4］Miao Qiang，Makis V．Extraction of machinery health index in CBM based on wavelet modulus maxima［C］//Flexible Automation and Intelligent Manufacturing．Toronto:［s.n.］，2004: 959-965．

［5］VecerP，Kreidl M，Smíd R．Condition indicators for gearbox condition monitoring systems［J］．Acta Polytechnical，2005，45(6) : 35-43．

［6］Luo Jianlu，Tan Xiaodong，Liu Ying，et al．A feature selection for fault prognosis based on fault evolution analysis: China，2014105317751［P］．2014-10-10．(in Chinese)罗建禄，谭晓栋，刘颖，等．一种基于故障演化分析的故障预测特征选择方法:中国，2014105317751 ［P］．2014-10-10．

［7］Lyu Kehong，Tan Xiaodong，Liu Guanjun，et al．Sensor selection of helicopter transmission systems based on physical model and sensitivity analysis［J］．Chinese Journal of Aeronautics，2014，27(3) : 643-654．

［8］Klutke G A，Kiessler P C，Wortman M A．A critical look at the bathtub curve［J］．IEEE Transactions on Reliability，2003，52(1) : 125-129．

［9］Zhang G F．Optimum test localization/selection in a diagnostic/prognosticarchitecture［D］．Atlanta(USA) : Georgia Institute of Technology，2005．

［10］Tian Zhigang，Zuo M J，Wu Siyan．Crack propagation assessment for spur gears using model-based analysis and simulation［J］．Journal of Intelligent Manufacturing，2012，23(2) : 239-253．

［11］Tan Xiaodong，Qiu Jing，Liu Guanjun，et al．A fault state recognition method based on wavelet energy entropy and hidden semi-Markov models and its applications［J］．Mechanical Science and Technology for Aerospace Engineering，2009，28(10) : 1340-1343．(in Chinese)谭晓栋，邱静，刘冠军，等．基于小波能谱熵-隐半马尔可夫模型的故障识别方法及应用［J］．机械科学与技术，2009，28(10) : 1340-1343．

［12］Chen Zaigang，Shao Yimin．Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth［J］．Engineering Failure Analysis，2011，18: 2149-2164．

【中文责编:英子;英文责编:雨辰】

A feature selection for fault prognosis based on fault evolution analysis

Fu Pengcheng1，2，Wang Changming1，Duan Junbin2，and Tan Xiaodong3

1) School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，P．R．China

2) Beijing Special Electromechanical Technology Research Institute，Beijing 100012，P．R．China

3) Department of Electronic Technology，Officers College of CAPF，Chengdu 610213，P．R．China

Abstract:In order to improve the reliability and the effectiveness of gear fault prognosis，we propose a feature selection based on fault evolution analysis．Firstly，we build a mechanical dynamics and vibration model，which accordingly generates dynamic responses with tooth damage growth．Secondly，we obtain the trend curves of gear fault evolution for several features，and calculate the track ability for gear fault evolution of each feature．The feature with the strongest track ability is chosen as the feature for gear fault prognosis．Finally，we use a gear crack fault in a onestage gearbox to verify the performance of the proposed method．Results show that the wavelet energy entropy with the optimal track ability for gear crack evolution among several selected features is the most suitable feature for gear crack fault prognosis．

Key words:mechanical dynamics and vibration; gear; feature selection; fault prognosis; fault evolution analysis; track ability; wavelet entropy

作者简介:傅鹏程(1972—)，男(汉族)，山西省阳泉市人，南京理工大学博士研究生，北京特种机电技术研究所高级工程师．E-mail: fang820729@ sina.com

基金项目:高等学校博士学科点专项科研基金资助项目(20133219110027)

doi:10．3724/SP．J．1249．2015．04434

文献标志码:A

中图分类号:TP 165